七年级数学平均数、中位数、众数
文档属性
| 名称 | 七年级数学平均数、中位数、众数 |

|
|
| 格式 | zip | ||
| 文件大小 | 274.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-12 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
数据的集中程度
平均数、中位数、众数
知识点回顾:
对于n个数x1,x2, …,xn,我们把
叫做这n个数的算术平均数, 简称平均数, 记为 ,读作“x拔”
1.算术平均数:
2.加权平均数:
一般地,若n个数x1,x2,…,xn的
权分别是w1,w2,…,wn ,则这n个数据的加权平均数为
=
①一般的:当一组数据x1, x2, …, xn的各个数值在一个常数a 的附近波动时,我们可以把各个数据同时减去这个常数 a ,得到一组新数据,求出新数据的平均数
② 当一组数据中的若干个数据多次重复出现:一般的, 如果在n个数中,x1出现n1次,x2出现n2次, …,xk出现nk次, (这里n1+n2+…+nk=n),那么
公式拓展:
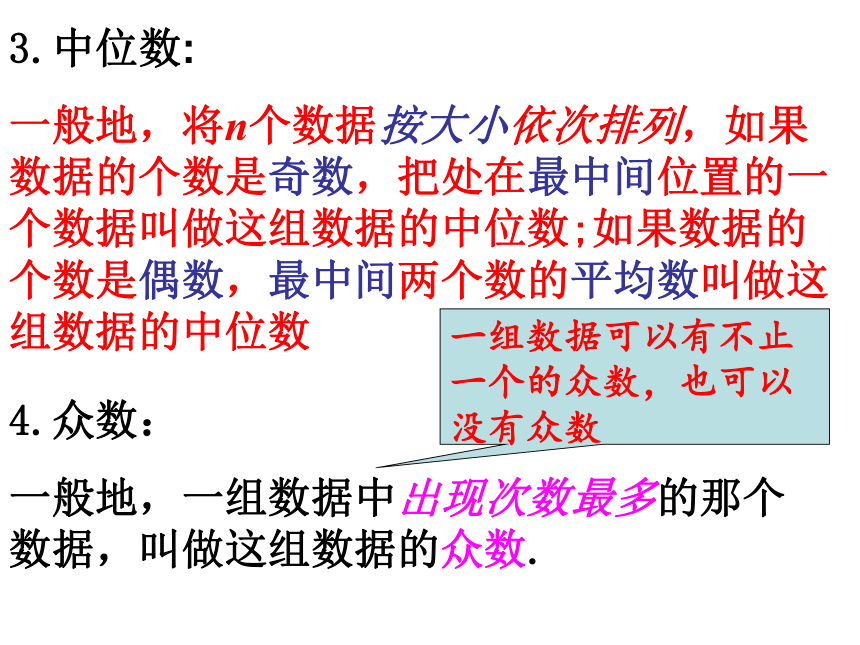
3.中位数:
一般地,将n个数据按大小依次排列,如果数据的个数是奇数,把处在最中间位置的一个数据叫做这组数据的中位数;如果数据的个数是偶数,最中间两个数的平均数叫做这组数据的中位数
4.众数:
一般地,一组数据中出现次数最多的那个数据,叫做这组数据的众数.
一组数据可以有不止一个的众数,也可以没有众数
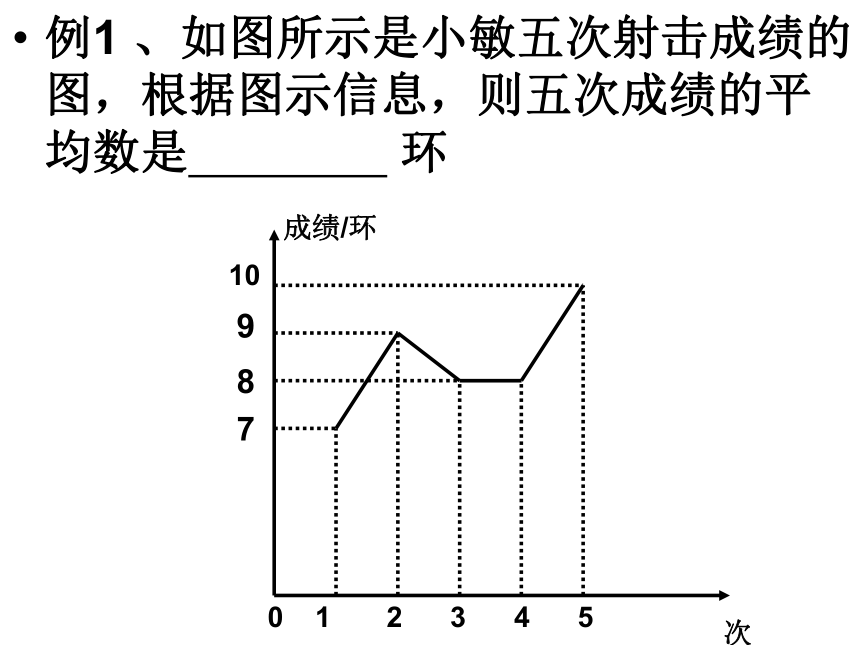
例1 、如图所示是小敏五次射击成绩的图,根据图示信息,则五次成绩的平均数是 环
成绩/环
次
0 1 2 3 4 5
10
9
8
7
例2、某学校举行实践操作技能大赛,所有参赛选手的成绩统计如下表所示,求本次参赛学生的平均成绩
分数 7.1 7.4 7.7 7.9 8.4 8.8 9 9.2 9.4 9.6
人数 1 2 3 2 1 5 4 6 5 1
2、有一组数据,各个数据之和为505,如果它们的平均数为101,那么这组数据的个数为_____.
4、有五盒火柴,每盒火柴的根数如下:71 ,73 ,76, 77, 78则每盒火柴的平均根数是___.
巩固提高
1、若4、x、5的平均数是7,则3、4、5、x、6这五个数的平均数是___
3、如果x1,x2,x3,x4,x5的平均数是20,那么5x1,5x2,5x3,5x4,5x5的平均数是_____.
6
5
100
75
5、5个数据的和为405,其中一个数据为85,那么另4个数据的平均数是_ .
80
6、若设一组数据x1、x2…….xn的平均数为m
1)x1+3, x2+3…… xn+3 的平均数为_____
2) 2x1、2x2…….2xn 的平均数为_____
3) 2x1+3, 2x2+3,……2xn+3 的平均数为_____
m+3
2m
2m+3
(1)105,103,101,100,114,108,110,
106,98,102;(共10个)
(2)4203,4204,4200,4194,4204,4210,
4195,4199.(共8个)
1.一组数据的平均数一定只有一个
x
√
2.一组数据的中位数一定只有一个
√
4.一组数据的众数一定只有一个
5.一组数据的平均数,中位数,中位数可以是同一个数
3.一组数据的中位数一定是这组数据中的某个数。
x
√
1,1,1,1,1
辨一辨
1,2,3,4,5,6
小试牛刀
1、 某公司欲招聘一名公关人员,对甲、乙两名候选人进行了面试和笔试,他们的成绩如下表所示:
候选人 测试成绩(百分制)
面试 笔试
甲 86 90
乙 92 83
(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取?
(2)如果公司认为,作为公关人员面试的成绩比笔试的成绩更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的平均成绩,看看谁被录取?
甲将被录取
乙将被录取
2.有十五位同学参加竞赛,且他们的
取八位同学进入决赛,某人知道了自己的分数以后,还需知道这十五位同学的分数的什么量,就能判断他能不能进入决赛?
分数互不相同,
3.一家鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如下表所示:
如果你是经理,请问你关注的是什么?你打算怎样进货呢?
尺码/厘米 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 11 7 3 1
Excel
甲、乙两班同学举行电脑汉字输入速度比赛,各派10名选手参加,参赛选手每分输入汉字个数统计如下:
输入汉字(个) 132 133 134 135 136 137 众数 中位数 平均数
甲班学生(人) 1 0 1 5 2 1
乙班学生(人) 0 1 4 1 2 2
分别求出各班选手每分输入汉字个数的平均数、 中位数和众数,并填入上表。
135
135
135
134
134.5
134.9
某校为了了解开展“孝敬父母,从家务事做起”活动的实施情况, 抽取八年级某班50名学生,调查他们一周做家务所用时间,得到一组数据,并绘制成下表,请根据下表完成各题:
(1)填写图中未完成的部分,
8
2.44
(3)这组数据的中位数是_________,众数是________,
2.5
3
你来发表看法
(2)该班学生每周做家务的平均时间是______,
每周做家务的时间(小时) 0 1 1.5 2 2.5 3 3.5 4 合计
人数 2 2 6 12 13 4 3 50
A公司和B公司去年用于工人工资、培训费用、保险支出均分别为72万元、36万元和12万元。 A公司今年这3项支出依次比去年增长了10%、20%和30%, B公司今年这3项支出依次比去年增长了30%、10%和20%, A、B公司今年这3项总支出比去年增长的百分数相等吗?它们分别是多少?
解:不相等;
小明家的鱼塘中养了某种鱼2000条,现准备捕捞出售。为了估计销售这种鱼的总收入,现从鱼塘中捕捞了3次,得到的数据如下表:
鱼的条数 平均每条鱼的质量/kg
第1次捕捞 15 1.6
第2次捕捞 15 2.0
第3次捕捞 10 1.8
(1)如果这3次捕捞的每条鱼的质量的平均数能够反映鱼塘中种鱼的基本情况,那么鱼塘中种鱼的总质量大约有多少千克?(2)如将鱼塘中这些鱼不分大小,按7.5元/kg的价格销售,小明家的收入大约有多少?
区别:计算平均数时,所有数据都参加运算,它能充分利用数据所提供的信息,但容易受极端值的影响。它应用最为广泛。
中位数的优点是计算简单,只与其在数据中的位置有关。但不能充分利用所有的数据信息。
众数只与其在数据中重复的次数有关,而且往往不是唯一的。 但不能充分利用所有的数据信息。而且当各个数据的重复次数大致相等时,众数往往没有特别的意义。
平均数、中位数和众数的联系与区别
联系:它们从不同角度描述了一组数据的集中程度,刻画了一组数据的平均水平。
数据的集中程度
平均数、中位数、众数
知识点回顾:
对于n个数x1,x2, …,xn,我们把
叫做这n个数的算术平均数, 简称平均数, 记为 ,读作“x拔”
1.算术平均数:
2.加权平均数:
一般地,若n个数x1,x2,…,xn的
权分别是w1,w2,…,wn ,则这n个数据的加权平均数为
=
①一般的:当一组数据x1, x2, …, xn的各个数值在一个常数a 的附近波动时,我们可以把各个数据同时减去这个常数 a ,得到一组新数据,求出新数据的平均数
② 当一组数据中的若干个数据多次重复出现:一般的, 如果在n个数中,x1出现n1次,x2出现n2次, …,xk出现nk次, (这里n1+n2+…+nk=n),那么
公式拓展:
3.中位数:
一般地,将n个数据按大小依次排列,如果数据的个数是奇数,把处在最中间位置的一个数据叫做这组数据的中位数;如果数据的个数是偶数,最中间两个数的平均数叫做这组数据的中位数
4.众数:
一般地,一组数据中出现次数最多的那个数据,叫做这组数据的众数.
一组数据可以有不止一个的众数,也可以没有众数
例1 、如图所示是小敏五次射击成绩的图,根据图示信息,则五次成绩的平均数是 环
成绩/环
次
0 1 2 3 4 5
10
9
8
7
例2、某学校举行实践操作技能大赛,所有参赛选手的成绩统计如下表所示,求本次参赛学生的平均成绩
分数 7.1 7.4 7.7 7.9 8.4 8.8 9 9.2 9.4 9.6
人数 1 2 3 2 1 5 4 6 5 1
2、有一组数据,各个数据之和为505,如果它们的平均数为101,那么这组数据的个数为_____.
4、有五盒火柴,每盒火柴的根数如下:71 ,73 ,76, 77, 78则每盒火柴的平均根数是___.
巩固提高
1、若4、x、5的平均数是7,则3、4、5、x、6这五个数的平均数是___
3、如果x1,x2,x3,x4,x5的平均数是20,那么5x1,5x2,5x3,5x4,5x5的平均数是_____.
6
5
100
75
5、5个数据的和为405,其中一个数据为85,那么另4个数据的平均数是_ .
80
6、若设一组数据x1、x2…….xn的平均数为m
1)x1+3, x2+3…… xn+3 的平均数为_____
2) 2x1、2x2…….2xn 的平均数为_____
3) 2x1+3, 2x2+3,……2xn+3 的平均数为_____
m+3
2m
2m+3
(1)105,103,101,100,114,108,110,
106,98,102;(共10个)
(2)4203,4204,4200,4194,4204,4210,
4195,4199.(共8个)
1.一组数据的平均数一定只有一个
x
√
2.一组数据的中位数一定只有一个
√
4.一组数据的众数一定只有一个
5.一组数据的平均数,中位数,中位数可以是同一个数
3.一组数据的中位数一定是这组数据中的某个数。
x
√
1,1,1,1,1
辨一辨
1,2,3,4,5,6
小试牛刀
1、 某公司欲招聘一名公关人员,对甲、乙两名候选人进行了面试和笔试,他们的成绩如下表所示:
候选人 测试成绩(百分制)
面试 笔试
甲 86 90
乙 92 83
(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取?
(2)如果公司认为,作为公关人员面试的成绩比笔试的成绩更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的平均成绩,看看谁被录取?
甲将被录取
乙将被录取
2.有十五位同学参加竞赛,且他们的
取八位同学进入决赛,某人知道了自己的分数以后,还需知道这十五位同学的分数的什么量,就能判断他能不能进入决赛?
分数互不相同,
3.一家鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如下表所示:
如果你是经理,请问你关注的是什么?你打算怎样进货呢?
尺码/厘米 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 11 7 3 1
Excel
甲、乙两班同学举行电脑汉字输入速度比赛,各派10名选手参加,参赛选手每分输入汉字个数统计如下:
输入汉字(个) 132 133 134 135 136 137 众数 中位数 平均数
甲班学生(人) 1 0 1 5 2 1
乙班学生(人) 0 1 4 1 2 2
分别求出各班选手每分输入汉字个数的平均数、 中位数和众数,并填入上表。
135
135
135
134
134.5
134.9
某校为了了解开展“孝敬父母,从家务事做起”活动的实施情况, 抽取八年级某班50名学生,调查他们一周做家务所用时间,得到一组数据,并绘制成下表,请根据下表完成各题:
(1)填写图中未完成的部分,
8
2.44
(3)这组数据的中位数是_________,众数是________,
2.5
3
你来发表看法
(2)该班学生每周做家务的平均时间是______,
每周做家务的时间(小时) 0 1 1.5 2 2.5 3 3.5 4 合计
人数 2 2 6 12 13 4 3 50
A公司和B公司去年用于工人工资、培训费用、保险支出均分别为72万元、36万元和12万元。 A公司今年这3项支出依次比去年增长了10%、20%和30%, B公司今年这3项支出依次比去年增长了30%、10%和20%, A、B公司今年这3项总支出比去年增长的百分数相等吗?它们分别是多少?
解:不相等;
小明家的鱼塘中养了某种鱼2000条,现准备捕捞出售。为了估计销售这种鱼的总收入,现从鱼塘中捕捞了3次,得到的数据如下表:
鱼的条数 平均每条鱼的质量/kg
第1次捕捞 15 1.6
第2次捕捞 15 2.0
第3次捕捞 10 1.8
(1)如果这3次捕捞的每条鱼的质量的平均数能够反映鱼塘中种鱼的基本情况,那么鱼塘中种鱼的总质量大约有多少千克?(2)如将鱼塘中这些鱼不分大小,按7.5元/kg的价格销售,小明家的收入大约有多少?
区别:计算平均数时,所有数据都参加运算,它能充分利用数据所提供的信息,但容易受极端值的影响。它应用最为广泛。
中位数的优点是计算简单,只与其在数据中的位置有关。但不能充分利用所有的数据信息。
众数只与其在数据中重复的次数有关,而且往往不是唯一的。 但不能充分利用所有的数据信息。而且当各个数据的重复次数大致相等时,众数往往没有特别的意义。
平均数、中位数和众数的联系与区别
联系:它们从不同角度描述了一组数据的集中程度,刻画了一组数据的平均水平。
