2020-2021学年鲁教五四版七年级下册数学期末冲刺试题(Word版,附答案解析)
文档属性
| 名称 | 2020-2021学年鲁教五四版七年级下册数学期末冲刺试题(Word版,附答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 210.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-19 00:00:00 | ||
图片预览




文档简介
2020-2021学年鲁教五四新版七年级下册数学期末冲刺试题
一.选择题(共10小题,满分30分,每小题3分)
1.|﹣2|等于( )
A.﹣2
B.﹣
C.2
D.
2.随着我国金融科技不断发展,网络消费、网上购物已成为人们生活不可或缺的一部分,今年“双十一”天猫成交额高达2684亿元.将数据“2684亿”用科学记数法表示( )
A.2.684×103
B.2.684×1011
C.2.684×1012
D.2.684×107
3.如图是由下列哪个立体图形展开得到的?( )
A.圆柱
B.三棱锥
C.三棱柱
D.四棱柱
4.若a,b均为整数,且b≠0,则不可能是( )
A.正数
B.负数
C.无理数
D.实数
5.在“科学与技术”知识竞赛的预选赛中,共有20道题,对于每一题,答对得10分,答错或不答扣5分,总得分不少于80分者通过预赛.育才中学有25名学生通过了预赛,他们分别可能答对的题数是( )
A.8道
B.12道
C.不少于12道
D.多于12道
6.下列说法正确的个数有( )
①﹣0.5x2y3与5y2x3是同类项;
②2π与﹣4不是同类项;
③两个单项式的和一定是多项式;
④单项式mn3的系数与次数之和为4.
A.4个
B.3个
C.1个
D.0个
7.如图,已知AB∥CD,∠1=125°,∠2=55°,则∠C=( )
A.45°
B.50°
C.70°
D.65°
8.在平面直角坐标系中,点A(﹣11,12)所在的象限为( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
9.如果b>a>0,那么( )
A.
B.
C.
D.﹣b>﹣a
10.如图所示,把多块大小不同的30°角三角板,摆放在平面直角坐标系中,第一块三角板AOB的一条直角边与x轴重合且点A的坐标为(2,0),∠ABO=30°,第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交x轴于点B1,第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交y轴于点B2,第四块三角板斜边B2B3与第三块三角板的斜边B1B2垂直且交x轴于点B3.按此规律继续下去,则线段OB2020的长为( )
A.2×()2020
B.2×()2021
C.()2020
D.()2021
二.填空题(共5小题,满分15分,每小题3分)
11.如图,将一副三角板叠放在一起,使直角顶点重合于O,则∠AOC+∠DOB=
.
12.一个正数a的平方根分别是2m﹣1和﹣3m+,则这个正数a为
.
13.若满足方程组的解x与y互为相反数,则k的值为
.
14.如图,AB∥CD,AC⊥AD,∠ACD=50°,则∠BAD的度数为
.
15.在平面直角坐标系中,点M(a﹣3,a+4),点N(5,9),若MN∥y轴,则a=
.
三.解答题(共8小题,满分80分)
16.解不等式组.,把不等式组的解集在数轴上表示出来.
17.某学校为了解本校九年级学生每周课外阅读时间的情况,从本校九年级600名学生中随机抽取40名学生,对其每周的课外阅读时间进行问卷调查,调查结果统计如下:
5.1
5.1
6.2
6.2
5.9
6.8
2.5
3.7
4.8
6.6
6.5
3.2
2.8
6.1
5.4
5.2
6.4
5.5
3.2
6.1
3.7
5.5
4.9
4.7
6.6
3.7
2.8
3.3
4.2
3.9
3.8
4.5
6.1
2.1
6.6
6.3
5.5
5.8
2.2
5.5
根据收集的数据绘制了如下的表格和统计图:
等级
每周课外阅读时间x/h
人数
A
2<x≤3
5
B
3<x≤4
8
C
4<x≤5
m
D
5<x≤6
n
E
6<x≤7
12
根据上面提供的信息,回答下列问题:
(1)统计表中的m=
,n=
;
(2)扇形统计图中,C所在扇形的圆心角度数为
;
(3)请根据调查结果,估计该校九年级学生课外阅读时间的等级为E的人数.
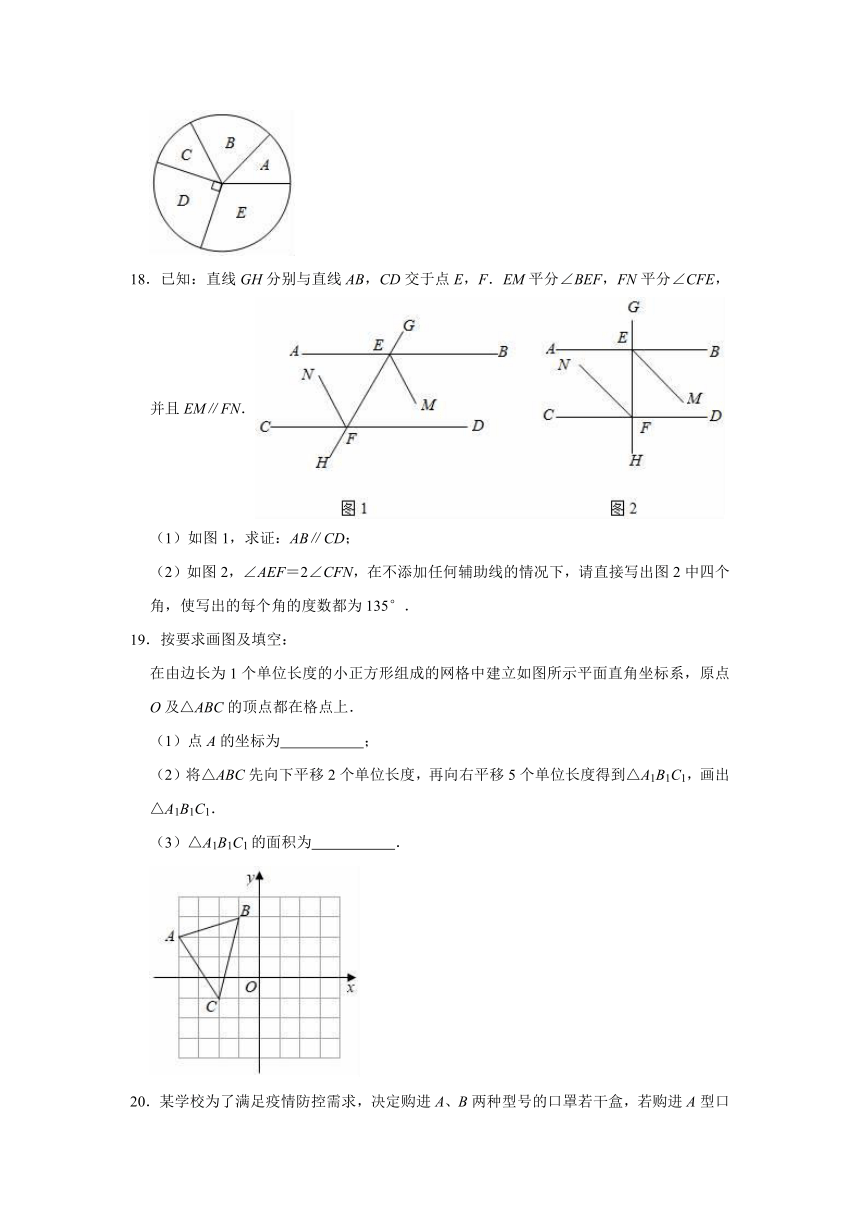
18.已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
19.按要求画图及填空:
在由边长为1个单位长度的小正方形组成的网格中建立如图所示平面直角坐标系,原点O及△ABC的顶点都在格点上.
(1)点A的坐标为
;
(2)将△ABC先向下平移2个单位长度,再向右平移5个单位长度得到△A1B1C1,画出△A1B1C1.
(3)△A1B1C1的面积为
.
20.某学校为了满足疫情防控需求,决定购进A、B两种型号的口罩若干盒,若购进A型口罩10盒,B型口罩5盒,共需1000元,若购进A型口罩4盒,B型口罩3盒,共需550元.
(1)求A、B两种型号的口罩每盒各需多少元?
(2)若该学校决定购进这两种型号的口罩共计200盒,并要求购进A型口罩的盒数不超过B型口罩盒数的4倍,请为该学校设计出最省钱的购买方案,并说明理由.
21.如图,直线AB、CD相交于点O,∠AOD=2∠BOD,OE平分∠BOD,OF平分∠COE.
(1)求∠DOE的度数;
(2)求∠AOF的度数.
22.已知a是的整数部分,b是它的小数部分,求(﹣a)3+b2的值.
23.如图,已知AM∥BN,∠A=80°,点P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,交射线AM于点C,D.(推理时不需要写出每一步的理由)
(1)求∠CBD的度数.
(2)当点P运动时,那么∠APB与∠ADB的大小关系是否发生变化?若不变,请找出它们的关系并说明理由;若变化,请找出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:由于|﹣2|=2,故选:C.
2.解:将2684亿=268400000000用科学记数法表示为:2.684×1011.
故选:B.
3.解:由图可得,该展开图是由三棱柱得到的,
故选:C.
4.解:∵a,b均为整数,且b≠0,
∴是一个分数,既为有理数,
∴不可能是无理数,
故选:C.
5.解:他们分别答对的题数是x道.
依题意可得:10x﹣5(20﹣x)≥80,
解得x≥12,
答:他们分别可能答对的题数不少于12道.
故选:C.
6.解:①﹣0.5x2y3与5y2x3不是同类项,错误;
②2π与﹣4是同类项,错误;
③两个单项式的和不一定是多项式,错误;
④单项式mn3的系数与次数之和为5,错误.
故选:D.
7.解:∵AB∥CD,∠1=125°,
∴∠FGD=∠1=125°,
∵∠2=55°,
∴∠C=∠FGD﹣∠2=125°﹣55°=70°,
故选:C.
8.解:点A(﹣11,12)所在象限为第二象限.
故选:B.
9.解:∵b>a>0,
∴<,故选项B错误
∴﹣>﹣,故选项A错误、C正确;
∵b>a,
∴﹣b<﹣a,故选项D错误.
故选:C.
10.解:由题意可得,
∵OB=OA?tan60°=2×=2,
∴B(0,2),
∵OB1=OB?tan60°=2×=2×()2,
∴B1(﹣2×()2,0),
∵OB2=OB1?tan60°=2×()3,
∴B2(0,﹣2×()3),
∵OB3=OB2?tan60°=2×()4,
∴B3(2×()4,0),
……
∴线段OB2020的长为2×()2021.
故选:B.
二.填空题(共5小题,满分15分,每小题3分)
11.解:设∠AOD=a,∠AOC=90°+a,∠BOD=90°﹣a,
所以∠AOC+∠BOD=90°+a+90°﹣a=180°.
故答案为:180°.
12.解:根据题意,得:2m﹣1+(﹣3m+)=0,
解得:m=,
∴正数a=(2×﹣1)2=4,
故答案为:4.
13.解:由题意得:y=﹣x,
代入方程组得:,
消去x得:,
解得:k=﹣11
故答案为:﹣11.
14.解:∵AC⊥AD,
∴∠CAD=90°,
∵∠ACD=50°,
∴∠ADC=180°﹣∠CAD﹣∠ACD=40°,
∵AB∥CD,
∴∠BAD=∠ADC=40°,
故答案为:40°.
15.解:∵MN∥y轴,
∴点M(a﹣3,a+4)与点N(5,9)的横坐标相同,
∴a﹣3=5,
∴a=8.
故答案为:8.
三.解答题(共8小题,满分80分)
16.解:解不等式2x+5≤3(x+2),得:x≥﹣1,
解不等式2x﹣<1,得:x<3,
则不等式组的解集为﹣1≤x<3,
将解集表示在数轴上如下:
17.解:(1)由扇形统计图可知,D等级所在扇形的圆心角度数为90°,
故抽取的学生中,D等级的学生有40×=10(名),m=5,n=10;
故C等级的学生有40﹣5﹣8﹣10﹣12=5(名),
故m=5,n=10.
故答案为:5;10;
(2)360°×=45°,
故扇形统计图中,C所在扇形的圆心角度数为45°;
(3)600×=180(名),
答:估计该校九年级学生课外阅读时间的等级为E的学生有180名.
18.(1)证明:∵EM∥FN,
∴∠EFN=∠FEM.
∵EM平分∠BEF,FN平分∠CFE,
∴∠CFE=2∠EFN,∠BEF=2∠FEM.
∴∠CFE=∠BEF.
∴AB∥CD.
(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵FN平分∠CFE,
∴∠CFE=2∠CFN,
∵∠AEF=2∠CFN,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=45°,
∴∠DFN=∠HFN=180°﹣45°=135°,
同理:∠AEM=∠GEM=135°.
∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.
19.解:(1)如图所示:点A的坐标为(﹣4,2);
故答案为:(﹣4,2);
(2)如图所示:△A1B1C1,即为所求;
(3)△A1B1C1的面积为:3×4﹣×1×3﹣×2×3﹣×1×4=5.5.
故答案为:5.5.
20.解:(1)设购进A型口罩每盒需x元,B型口罩每盒需y元,
依题意,得:,
解得:,
答:A型口罩每盒需25元,B型口罩每盒需150元;
(2)设购进m盒A型口罩,则购进(200﹣m)盒B型口罩,
依题意,得:m≤4(200﹣m),
解得:m≤160.
设该学校购进这批口罩共花费w元,则w=25m+150(200﹣m)=﹣125m+30000.
∵﹣125<0,
∴w随m的增大而减小,
又∵m≤160,且m为整数,
∴当m=160时,w取得最小值,此时200﹣m=40.
∴最省钱的购买方案为:购进160盒A型口罩,40盒B型口罩.
21.解:(1)∵∠AOD+∠BOD=180°,∠AOD=2∠BOD,
∴∠AOD=180°×=120°,∠BOD=180°×=60°,
∵OE平分∠BOD,
∴∠DOE=∠BOE=∠BOD=30°,
(2)∵∠COE+∠DOE=180°,
∴∠COE=180°﹣∠DOE=180°﹣30°=150°,
∵OF平分∠COE,
∴∠COF=∠EOF=∠COE=×150°=75°,
又∵∠AOC=∠BOD=60°,
∴∠AOF=∠AOC+∠COF=60°+75°=135°.
22.解:∵3<a<4,
∴a=3,b=﹣3,
∴原式=(﹣3)3+(﹣3)2
=﹣27+(10+9)
=﹣27+10﹣6+9
=.
23.解:(1)∵AM∥BN,
∴∠ABN+∠A=180°,
∴∠ABN=180°﹣80°=100°,
∴∠ABP+∠PBN=10°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=100°,
∴∠CBD=∠CBP+∠DBP=50°;
(2)不变,∠APB:∠ADB=2:1.
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB:∠ADB=2:1;
(3)∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,则有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN,
由(1)可知∠ABN=100°,∠CBD=50°,
∴∠ABC+∠DBN=50°,
∴∠ABC=25°.
一.选择题(共10小题,满分30分,每小题3分)
1.|﹣2|等于( )
A.﹣2
B.﹣
C.2
D.
2.随着我国金融科技不断发展,网络消费、网上购物已成为人们生活不可或缺的一部分,今年“双十一”天猫成交额高达2684亿元.将数据“2684亿”用科学记数法表示( )
A.2.684×103
B.2.684×1011
C.2.684×1012
D.2.684×107
3.如图是由下列哪个立体图形展开得到的?( )
A.圆柱
B.三棱锥
C.三棱柱
D.四棱柱
4.若a,b均为整数,且b≠0,则不可能是( )
A.正数
B.负数
C.无理数
D.实数
5.在“科学与技术”知识竞赛的预选赛中,共有20道题,对于每一题,答对得10分,答错或不答扣5分,总得分不少于80分者通过预赛.育才中学有25名学生通过了预赛,他们分别可能答对的题数是( )
A.8道
B.12道
C.不少于12道
D.多于12道
6.下列说法正确的个数有( )
①﹣0.5x2y3与5y2x3是同类项;
②2π与﹣4不是同类项;
③两个单项式的和一定是多项式;
④单项式mn3的系数与次数之和为4.
A.4个
B.3个
C.1个
D.0个
7.如图,已知AB∥CD,∠1=125°,∠2=55°,则∠C=( )
A.45°
B.50°
C.70°
D.65°
8.在平面直角坐标系中,点A(﹣11,12)所在的象限为( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
9.如果b>a>0,那么( )
A.
B.
C.
D.﹣b>﹣a
10.如图所示,把多块大小不同的30°角三角板,摆放在平面直角坐标系中,第一块三角板AOB的一条直角边与x轴重合且点A的坐标为(2,0),∠ABO=30°,第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交x轴于点B1,第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交y轴于点B2,第四块三角板斜边B2B3与第三块三角板的斜边B1B2垂直且交x轴于点B3.按此规律继续下去,则线段OB2020的长为( )
A.2×()2020
B.2×()2021
C.()2020
D.()2021
二.填空题(共5小题,满分15分,每小题3分)
11.如图,将一副三角板叠放在一起,使直角顶点重合于O,则∠AOC+∠DOB=
.
12.一个正数a的平方根分别是2m﹣1和﹣3m+,则这个正数a为
.
13.若满足方程组的解x与y互为相反数,则k的值为
.
14.如图,AB∥CD,AC⊥AD,∠ACD=50°,则∠BAD的度数为
.
15.在平面直角坐标系中,点M(a﹣3,a+4),点N(5,9),若MN∥y轴,则a=
.
三.解答题(共8小题,满分80分)
16.解不等式组.,把不等式组的解集在数轴上表示出来.
17.某学校为了解本校九年级学生每周课外阅读时间的情况,从本校九年级600名学生中随机抽取40名学生,对其每周的课外阅读时间进行问卷调查,调查结果统计如下:
5.1
5.1
6.2
6.2
5.9
6.8
2.5
3.7
4.8
6.6
6.5
3.2
2.8
6.1
5.4
5.2
6.4
5.5
3.2
6.1
3.7
5.5
4.9
4.7
6.6
3.7
2.8
3.3
4.2
3.9
3.8
4.5
6.1
2.1
6.6
6.3
5.5
5.8
2.2
5.5
根据收集的数据绘制了如下的表格和统计图:
等级
每周课外阅读时间x/h
人数
A
2<x≤3
5
B
3<x≤4
8
C
4<x≤5
m
D
5<x≤6
n
E
6<x≤7
12
根据上面提供的信息,回答下列问题:
(1)统计表中的m=
,n=
;
(2)扇形统计图中,C所在扇形的圆心角度数为
;
(3)请根据调查结果,估计该校九年级学生课外阅读时间的等级为E的人数.
18.已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
19.按要求画图及填空:
在由边长为1个单位长度的小正方形组成的网格中建立如图所示平面直角坐标系,原点O及△ABC的顶点都在格点上.
(1)点A的坐标为
;
(2)将△ABC先向下平移2个单位长度,再向右平移5个单位长度得到△A1B1C1,画出△A1B1C1.
(3)△A1B1C1的面积为
.
20.某学校为了满足疫情防控需求,决定购进A、B两种型号的口罩若干盒,若购进A型口罩10盒,B型口罩5盒,共需1000元,若购进A型口罩4盒,B型口罩3盒,共需550元.
(1)求A、B两种型号的口罩每盒各需多少元?
(2)若该学校决定购进这两种型号的口罩共计200盒,并要求购进A型口罩的盒数不超过B型口罩盒数的4倍,请为该学校设计出最省钱的购买方案,并说明理由.
21.如图,直线AB、CD相交于点O,∠AOD=2∠BOD,OE平分∠BOD,OF平分∠COE.
(1)求∠DOE的度数;
(2)求∠AOF的度数.
22.已知a是的整数部分,b是它的小数部分,求(﹣a)3+b2的值.
23.如图,已知AM∥BN,∠A=80°,点P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,交射线AM于点C,D.(推理时不需要写出每一步的理由)
(1)求∠CBD的度数.
(2)当点P运动时,那么∠APB与∠ADB的大小关系是否发生变化?若不变,请找出它们的关系并说明理由;若变化,请找出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:由于|﹣2|=2,故选:C.
2.解:将2684亿=268400000000用科学记数法表示为:2.684×1011.
故选:B.
3.解:由图可得,该展开图是由三棱柱得到的,
故选:C.
4.解:∵a,b均为整数,且b≠0,
∴是一个分数,既为有理数,
∴不可能是无理数,
故选:C.
5.解:他们分别答对的题数是x道.
依题意可得:10x﹣5(20﹣x)≥80,
解得x≥12,
答:他们分别可能答对的题数不少于12道.
故选:C.
6.解:①﹣0.5x2y3与5y2x3不是同类项,错误;
②2π与﹣4是同类项,错误;
③两个单项式的和不一定是多项式,错误;
④单项式mn3的系数与次数之和为5,错误.
故选:D.
7.解:∵AB∥CD,∠1=125°,
∴∠FGD=∠1=125°,
∵∠2=55°,
∴∠C=∠FGD﹣∠2=125°﹣55°=70°,
故选:C.
8.解:点A(﹣11,12)所在象限为第二象限.
故选:B.
9.解:∵b>a>0,
∴<,故选项B错误
∴﹣>﹣,故选项A错误、C正确;
∵b>a,
∴﹣b<﹣a,故选项D错误.
故选:C.
10.解:由题意可得,
∵OB=OA?tan60°=2×=2,
∴B(0,2),
∵OB1=OB?tan60°=2×=2×()2,
∴B1(﹣2×()2,0),
∵OB2=OB1?tan60°=2×()3,
∴B2(0,﹣2×()3),
∵OB3=OB2?tan60°=2×()4,
∴B3(2×()4,0),
……
∴线段OB2020的长为2×()2021.
故选:B.
二.填空题(共5小题,满分15分,每小题3分)
11.解:设∠AOD=a,∠AOC=90°+a,∠BOD=90°﹣a,
所以∠AOC+∠BOD=90°+a+90°﹣a=180°.
故答案为:180°.
12.解:根据题意,得:2m﹣1+(﹣3m+)=0,
解得:m=,
∴正数a=(2×﹣1)2=4,
故答案为:4.
13.解:由题意得:y=﹣x,
代入方程组得:,
消去x得:,
解得:k=﹣11
故答案为:﹣11.
14.解:∵AC⊥AD,
∴∠CAD=90°,
∵∠ACD=50°,
∴∠ADC=180°﹣∠CAD﹣∠ACD=40°,
∵AB∥CD,
∴∠BAD=∠ADC=40°,
故答案为:40°.
15.解:∵MN∥y轴,
∴点M(a﹣3,a+4)与点N(5,9)的横坐标相同,
∴a﹣3=5,
∴a=8.
故答案为:8.
三.解答题(共8小题,满分80分)
16.解:解不等式2x+5≤3(x+2),得:x≥﹣1,
解不等式2x﹣<1,得:x<3,
则不等式组的解集为﹣1≤x<3,
将解集表示在数轴上如下:
17.解:(1)由扇形统计图可知,D等级所在扇形的圆心角度数为90°,
故抽取的学生中,D等级的学生有40×=10(名),m=5,n=10;
故C等级的学生有40﹣5﹣8﹣10﹣12=5(名),
故m=5,n=10.
故答案为:5;10;
(2)360°×=45°,
故扇形统计图中,C所在扇形的圆心角度数为45°;
(3)600×=180(名),
答:估计该校九年级学生课外阅读时间的等级为E的学生有180名.
18.(1)证明:∵EM∥FN,
∴∠EFN=∠FEM.
∵EM平分∠BEF,FN平分∠CFE,
∴∠CFE=2∠EFN,∠BEF=2∠FEM.
∴∠CFE=∠BEF.
∴AB∥CD.
(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵FN平分∠CFE,
∴∠CFE=2∠CFN,
∵∠AEF=2∠CFN,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=45°,
∴∠DFN=∠HFN=180°﹣45°=135°,
同理:∠AEM=∠GEM=135°.
∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.
19.解:(1)如图所示:点A的坐标为(﹣4,2);
故答案为:(﹣4,2);
(2)如图所示:△A1B1C1,即为所求;
(3)△A1B1C1的面积为:3×4﹣×1×3﹣×2×3﹣×1×4=5.5.
故答案为:5.5.
20.解:(1)设购进A型口罩每盒需x元,B型口罩每盒需y元,
依题意,得:,
解得:,
答:A型口罩每盒需25元,B型口罩每盒需150元;
(2)设购进m盒A型口罩,则购进(200﹣m)盒B型口罩,
依题意,得:m≤4(200﹣m),
解得:m≤160.
设该学校购进这批口罩共花费w元,则w=25m+150(200﹣m)=﹣125m+30000.
∵﹣125<0,
∴w随m的增大而减小,
又∵m≤160,且m为整数,
∴当m=160时,w取得最小值,此时200﹣m=40.
∴最省钱的购买方案为:购进160盒A型口罩,40盒B型口罩.
21.解:(1)∵∠AOD+∠BOD=180°,∠AOD=2∠BOD,
∴∠AOD=180°×=120°,∠BOD=180°×=60°,
∵OE平分∠BOD,
∴∠DOE=∠BOE=∠BOD=30°,
(2)∵∠COE+∠DOE=180°,
∴∠COE=180°﹣∠DOE=180°﹣30°=150°,
∵OF平分∠COE,
∴∠COF=∠EOF=∠COE=×150°=75°,
又∵∠AOC=∠BOD=60°,
∴∠AOF=∠AOC+∠COF=60°+75°=135°.
22.解:∵3<a<4,
∴a=3,b=﹣3,
∴原式=(﹣3)3+(﹣3)2
=﹣27+(10+9)
=﹣27+10﹣6+9
=.
23.解:(1)∵AM∥BN,
∴∠ABN+∠A=180°,
∴∠ABN=180°﹣80°=100°,
∴∠ABP+∠PBN=10°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=100°,
∴∠CBD=∠CBP+∠DBP=50°;
(2)不变,∠APB:∠ADB=2:1.
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB:∠ADB=2:1;
(3)∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,则有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN,
由(1)可知∠ABN=100°,∠CBD=50°,
∴∠ABC+∠DBN=50°,
∴∠ABC=25°.
同课章节目录
