选修2-2 第2章推理与证明 基础测试题-2020-2021学年人教A版高二数学上学期期末复习(Word含解析)
文档属性
| 名称 | 选修2-2 第2章推理与证明 基础测试题-2020-2021学年人教A版高二数学上学期期末复习(Word含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 709.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-19 00:39:39 | ||
图片预览





文档简介
人教A版选修2-2推理与证明基础测试题
一、单选题
1.用数学归纳法证明时,第一步应验证的不等式是( )
A. B.
C. D.
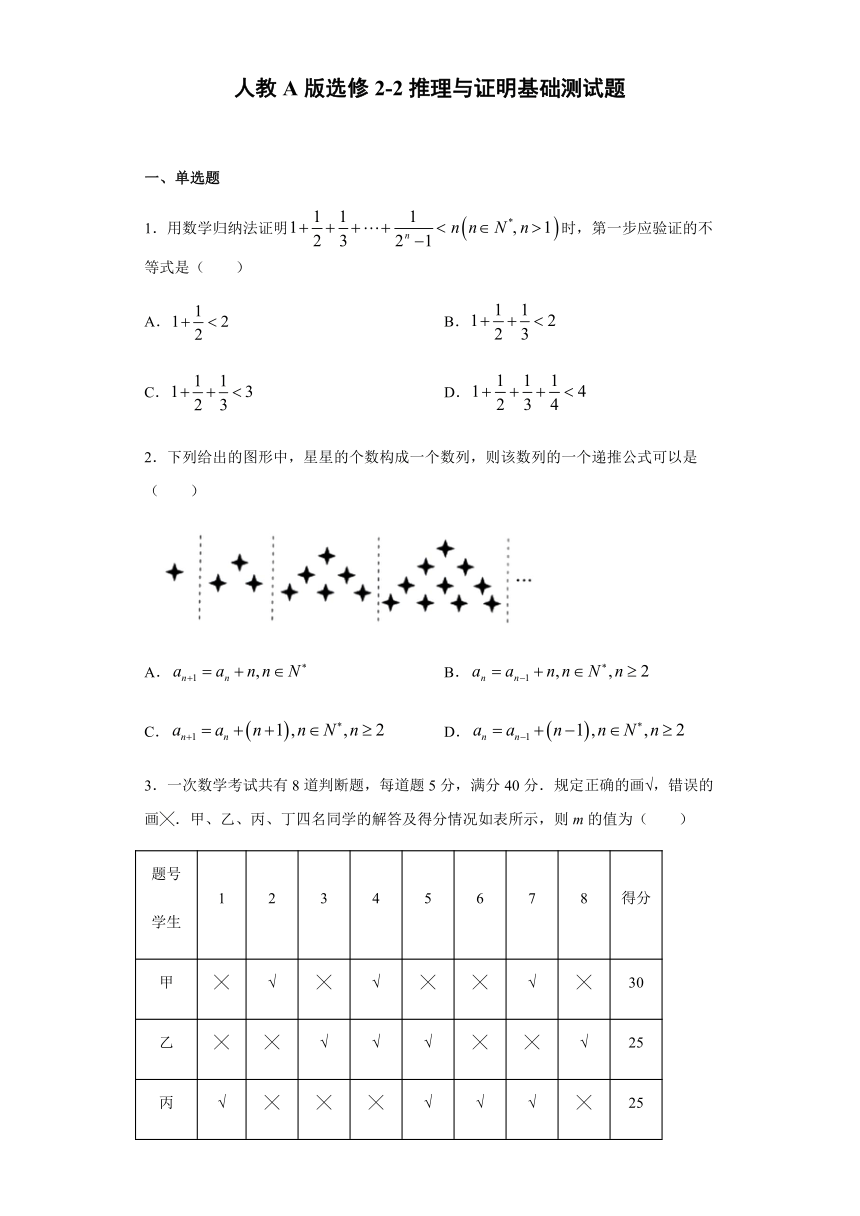
2.下列给出的图形中,星星的个数构成一个数列,则该数列的一个递推公式可以是( )
A. B.
C. D.
3.一次数学考试共有8道判断题,每道题5分,满分40分.规定正确的画√,错误的画╳.甲、乙、丙、丁四名同学的解答及得分情况如表所示,则m的值为( )
题号 学生 1 2 3 4 5 6 7 8 得分
甲 ╳ √ ╳ √ ╳ ╳ √ ╳ 30
乙 ╳ ╳ √ √ √ ╳ ╳ √ 25
丙 √ ╳ ╳ ╳ √ √ √ ╳ 25
丁 ╳ √ ╳ √ √ ╳ √ √ m
A.35 B.30 C.25 D.20
4.甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则( )
A.乙可以知道四人的成绩 B.丁可以知道四人的成绩
C.乙、丁可以知道对方的成绩 D.乙、丁可以知道自己的成绩
5.四个孩子在刘老师的后院玩球,突然传来一阵打碎玻璃的响声,刘老师跑去查看,发现一扇窗户玻璃被打破了,老师问:“是谁打破的?”
涛涛说:“是可可打破的.”
可可说:“是毛毛打破的.”
毛毛说:“可可说谎.”
多多说:“我没有打破玻璃.”
如果只有一个小孩说谎,那么打破玻璃的是谁?( )
A.涛涛 B.可可 C.毛毛 D.多多
6.“一切金属都能导电,铁是金属,所以铁能导电”.此推理方法是( )
A.类比推理 B.演绎推理 C.归纳推理 D.以上都不对
7.用数学归纳法证明等式时,当时,左边等于( )
A.1 B. C. D.
8.用数学归纳法证明等式,当时,等式左端应在的基础上加上( )
A. B. C.D.
9.用反证法证明命题“设、为实数,则方程至少有一个实根”时,要做的假设是( )
A.方程没有实根 B.方程至多有一个实根
C.方程至多有两个实根 D.方程恰好有两个实根
10.某西方国家流传这样的一个政治笑话:“鹅吃白菜,参议员先生也吃白菜,所以参议员先生是鹅”结论显然是错误的,是因为( )
A.大前提错误 B.推理形式错误
C.小前提错误 D.大、小前提、推理形式都错
11.观察下列各式,,,,,,…,则( )
A.47 B.76 C.121 D.123
12.欲证成立,只需证( )
A. B.
C. D.
二、填空题
13.用数学归纳法证明时,第一步应验证的等式是________.
14.用反证法证明:存在,,应先假设:________.
15.数学老师给同学们出了一道证明题,,,三名同学中只有一名同学写对了,当他们被问到谁写对了时,说:“没有写对”;说:“我写对了”;说:“说得是真话”.事实证明:在这三名同学中,只有一人说的是假话,那么说假话的同学是______.
16.若,,,一定有,成立,请将猜想结果填空:________.
三、解答题
17.证明:
18.已知数列第一项,且,
(1)计算的值.
(2)试猜想这个数列的通项公式(不用写出推导过程).
19.设数列的前项和为,且满足.
(1)求的值,并写出数列的通项公式;
(2)写出用三段论证明数列是等比数列的大提前、小前提、结论.
20.已知数列满足,.
(1)求、;
(2)猜想数列通项公式,并用数学归纳法给出证明.
21.已知、、,
(1)求证:;
(2)求证:;
(3)由(1)、(2),将命题推广到一般情形(不作证明).
22.某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
(1) 求出,,并猜测的表达式;
(2) 求证:+++…+.
参考答案
1.B
【分析】
根据,,由所取的第一个正整数为2求解.
【详解】
∵,,
∴所取的第一个正整数为2,又,
故第一步应验证.
故选:B
2.B
【分析】
本题可根据每一个图形与前一个图形的关系得出结论.
【详解】
结合图象易知,,,,,
故选:B.
3.B
【分析】
通过分析甲、乙、丙三人的答案以及得分情况,推理得出这8道判断的答案,从而可得结果.
【详解】
因为乙、丙第2,5题答案相同,且总得分相同,所以第2,5两题答案正确,
又因为甲得分30分即甲错两题且第2题、第5题答案均与乙丙不同,
故其余6题答案均正确,
故而这8道判断的答案分别是:╳╳╳√√╳√╳,
对比丁的答案,可知其2、8两题错误,故得分m=6×5=30,
故选:B.
4.D
【分析】
根据题中条件,直接分析,即可得出结果.
【详解】
由甲的说法可知乙、丙一人优秀一人良好,则甲、丁一人优秀一人良好,乙看到丙的结果则知道自己的结果,丁看到甲的结果则知道自己的结果.
故选:D.
5.B
【分析】
假设涛涛说谎,通过矛盾说明假设不成立即可得出结论.
【详解】
如果涛涛说谎,则毛毛没有说谎,即可可说谎,与只有一个小孩说谎矛盾,所以涛涛没有说谎,即玻璃是可可打破的.
故选:B.
6.B
【分析】
符合三段论:大前提,小前提,结论,所以是演绎推理.
【详解】
在推理的过程中:一切金属都能导电,是大前提,
铁是金属,是小前提,
所以铁能导电,是结论,
故是演绎推理,
故选:B
7.C
【分析】
根据题意,将直接代入,即可求出结果.
【详解】
用数学归纳法证明:,
在验证时,
令代入左边的代数式,得到左边.
故选:C
8.B
【分析】
写出和时的两式,然后比较可得.
【详解】
时等式为,
时等式为,
当时,等式左端应在的基础上加上,
故选:B.
【点睛】
本题考查数学归纳法,数学归纳法的关键、难点就在于用的假设结论证明的的结论,因此观察出与之间式子的关系至关重要.
9.A
【分析】
将命题的结论否定可得出结果.
【详解】
“方程至少有一个实根”的否定为“方程没有实根”.
因此,用反证法证明命题“设、为实数,则方程至少有一个实根”时,要做的假设是“方程没有实根”.
故选:A.
【点睛】
本题考查反证法,意在考查学生对反证法的理解,属于基础题.
10.B
【分析】
根据演绎推理的形式即可判断.
【详解】
大前提的形式: “鹅吃白菜”,不是全称命题,大前提本身正确,
小前提“参议员先生也吃白菜”本身也正确,但是不是大前提下的特殊情况,
鹅与人不能类比,
不符合三段论推理形式,推理形式错误.
故选:B
【点睛】
本题考查了知识点是演绎推理的基本方法,属于基础题.
11.B
【分析】
根据题目所给等式,归纳出正确结论.
【详解】
根据题目所给等式可知:,,.
故选:B
【点睛】
本小题主要考查合情推理,属于基础题.
12.C
【分析】
由于原不等式的等价于,再两边同时平方,即可得出答案.
【详解】
解:根据题意,欲证,
则需证,
只需证.
故选:C.
【点睛】
本题考查利用分析法证明不等式,体现转化思想,属于基础题.
13.
【分析】
在等式中令可得结果.
【详解】
由题知等式的左边有项,右边有项,且,因此第一步应验证时的等式,此时左边,右边,
故答案为:.
14.任意,
【分析】
由特称命题的否定可得解.
【详解】
反证法即为先假设命题的否定成立,及应先假设:任意,.
故答案为:任意,.
15.
【分析】
利用反证法即可得出结论
【详解】
假如说的是假话,则说的也是假话,不成立;
假如说的是假话,即没有写对,又没有写对,故写对了;
假如说的是假话,即写对了,则说的也是假话,不成立.
故说假话的同学是.
故答案为:B
【点睛】
此题考查简单的合情推理,考查学生分析解决问题的能力,属于基础题
16.
【分析】
根据表达式的规律即可猜想结论.
【详解】
解:由a>0,b>0,a+b=1,
一定有ab+≥4+,(ab)2+()2≥42+成立,
可以猜想:,
故答案为:.
【点睛】
本题考查了归纳推理的问题,关键找到规律,属于基础题.
17.证明见解析.
【分析】
利用题意,由分析法,原问题等价于,结合题意进行计算即可证得结论.
【详解】
证明:要证
只需证
只需证
只需证
只需证
因为成立,
所以.
【点睛】
本题考查分析法证明不等式,考查学生的逻辑推理能力,是一道容易题.
18.(1),,,(2)猜想
【分析】
(1)由数列递推式运算即可得解;重点考查了归纳推理能力,
(2)由前面有限项归纳通项公式即可得解.
【详解】
解:(1)由数列第一项,且,
则,,,
即,,,
(2)由,,,
猜想这个数列的通项公式为.
【点睛】
本题考查了数列递推式的运算,重点考查了归纳推理能力,属基础题.
19.(1),,,,;(2)见解析.
【分析】
(1)先求出的值,分析规律,再归纳出通项公式即可;
(2)将等比数列的定义作为大前提,然后将归纳得通项公式作为小前提,数列是等比数列则为结论.
【详解】
解:(1)由,
当时,,解得:,
当时,,解得:,
当时,,解得:,
由此归纳推理得:,.
(2)大前提:在数列中,若,是非零常数,则是等比数列;
小前提:在数列中,,;
结论:数列是等比数列.
【点睛】
本题考查了归纳推理,重点考查了三段论,属基础题.
20.(1),;(2),证明见解析.
【分析】
(1)依据递推关系可求、.
(2)根据(1)可猜测,按照数学归纳法的基本步骤证明即可.
【详解】
(1),;
(2)猜想数列通项公式,证明如下:
当时,,,所以成立;
假设时成立,即 ,
当时, ,
∴时,成立,
综上,由①②得: .
【点睛】
由数列的前若干项和递推关系可猜测数列的通项,然后再用数学归纳法去证明,注意数学归纳法有三个部分即归纳的起点、归纳假设和归纳证明,注意归纳证明的推理过程必须用到归纳假设.
21.(1)详见解析;
(2)详见解析;
(3).
【分析】
(1)对不等式分别使用基本不等式即可证明出;
(2)对不等式分别使用基本不等式即可证明出
;
(3)根据(1)(2)不等式的结构特征直接写出一般推广结论.
【详解】
(1)(当且仅当=1时取等号);
(2)(当且仅当时取等号);
(3)推广:已知,,…,则(当且仅当时取等号);
【点睛】
本题考查了基本不等式的应用与推广,考查了类比推理的能力.
22.(1) f(2)=5,f(3)=13,f(4)=25,f(5)=25+4×4=41.f(n)=2n2-2n+1.
(2)略
【解析】
本试题主要是考查了数列的归纳猜想思想的运用,根据前几项.来猜想并运用数学归纳法加以证明.
(1)结合题目中的 递推关系式可知前几项的值,并猜想结论.
(2)分为两步骤进行,先证明n取第一个值时成立,再假设n=k时成立,证明n=k+1时也成立即可.
解: (1)∵f(1)=1,f(2)=5,f(3)=13,f(4)=25,∴f(5)=25+4×4=41.
∵f(2)-f(1)=4=4×1,f(3)-f(2)=8=4×2,f(4)-f(3)=12=4×3,f(5)-f(4)=16=4×4,
由上式规律得出f(n+1)-f(n)=4n. ∴f(n)-f(n-1)=4(n-1),f(n-1)-f(n-2)=4·(n-2),
f(n-2)-f(n-3)=4·(n-3),…
f(2)-f(1)=4×1,
∴f(n)-f(1)=4[(n-1)+(n-2)+…+2+1]=2(n-1)·n,∴f(n)=2n2-2n+1(n≥2),
又n=1时,f(1)也适合f(n).
∴f(n)=2n2-2n+1. --------6分
---------------12分
一、单选题
1.用数学归纳法证明时,第一步应验证的不等式是( )
A. B.
C. D.
2.下列给出的图形中,星星的个数构成一个数列,则该数列的一个递推公式可以是( )
A. B.
C. D.
3.一次数学考试共有8道判断题,每道题5分,满分40分.规定正确的画√,错误的画╳.甲、乙、丙、丁四名同学的解答及得分情况如表所示,则m的值为( )
题号 学生 1 2 3 4 5 6 7 8 得分
甲 ╳ √ ╳ √ ╳ ╳ √ ╳ 30
乙 ╳ ╳ √ √ √ ╳ ╳ √ 25
丙 √ ╳ ╳ ╳ √ √ √ ╳ 25
丁 ╳ √ ╳ √ √ ╳ √ √ m
A.35 B.30 C.25 D.20
4.甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则( )
A.乙可以知道四人的成绩 B.丁可以知道四人的成绩
C.乙、丁可以知道对方的成绩 D.乙、丁可以知道自己的成绩
5.四个孩子在刘老师的后院玩球,突然传来一阵打碎玻璃的响声,刘老师跑去查看,发现一扇窗户玻璃被打破了,老师问:“是谁打破的?”
涛涛说:“是可可打破的.”
可可说:“是毛毛打破的.”
毛毛说:“可可说谎.”
多多说:“我没有打破玻璃.”
如果只有一个小孩说谎,那么打破玻璃的是谁?( )
A.涛涛 B.可可 C.毛毛 D.多多
6.“一切金属都能导电,铁是金属,所以铁能导电”.此推理方法是( )
A.类比推理 B.演绎推理 C.归纳推理 D.以上都不对
7.用数学归纳法证明等式时,当时,左边等于( )
A.1 B. C. D.
8.用数学归纳法证明等式,当时,等式左端应在的基础上加上( )
A. B. C.D.
9.用反证法证明命题“设、为实数,则方程至少有一个实根”时,要做的假设是( )
A.方程没有实根 B.方程至多有一个实根
C.方程至多有两个实根 D.方程恰好有两个实根
10.某西方国家流传这样的一个政治笑话:“鹅吃白菜,参议员先生也吃白菜,所以参议员先生是鹅”结论显然是错误的,是因为( )
A.大前提错误 B.推理形式错误
C.小前提错误 D.大、小前提、推理形式都错
11.观察下列各式,,,,,,…,则( )
A.47 B.76 C.121 D.123
12.欲证成立,只需证( )
A. B.
C. D.
二、填空题
13.用数学归纳法证明时,第一步应验证的等式是________.
14.用反证法证明:存在,,应先假设:________.
15.数学老师给同学们出了一道证明题,,,三名同学中只有一名同学写对了,当他们被问到谁写对了时,说:“没有写对”;说:“我写对了”;说:“说得是真话”.事实证明:在这三名同学中,只有一人说的是假话,那么说假话的同学是______.
16.若,,,一定有,成立,请将猜想结果填空:________.
三、解答题
17.证明:
18.已知数列第一项,且,
(1)计算的值.
(2)试猜想这个数列的通项公式(不用写出推导过程).
19.设数列的前项和为,且满足.
(1)求的值,并写出数列的通项公式;
(2)写出用三段论证明数列是等比数列的大提前、小前提、结论.
20.已知数列满足,.
(1)求、;
(2)猜想数列通项公式,并用数学归纳法给出证明.
21.已知、、,
(1)求证:;
(2)求证:;
(3)由(1)、(2),将命题推广到一般情形(不作证明).
22.某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
(1) 求出,,并猜测的表达式;
(2) 求证:+++…+.
参考答案
1.B
【分析】
根据,,由所取的第一个正整数为2求解.
【详解】
∵,,
∴所取的第一个正整数为2,又,
故第一步应验证.
故选:B
2.B
【分析】
本题可根据每一个图形与前一个图形的关系得出结论.
【详解】
结合图象易知,,,,,
故选:B.
3.B
【分析】
通过分析甲、乙、丙三人的答案以及得分情况,推理得出这8道判断的答案,从而可得结果.
【详解】
因为乙、丙第2,5题答案相同,且总得分相同,所以第2,5两题答案正确,
又因为甲得分30分即甲错两题且第2题、第5题答案均与乙丙不同,
故其余6题答案均正确,
故而这8道判断的答案分别是:╳╳╳√√╳√╳,
对比丁的答案,可知其2、8两题错误,故得分m=6×5=30,
故选:B.
4.D
【分析】
根据题中条件,直接分析,即可得出结果.
【详解】
由甲的说法可知乙、丙一人优秀一人良好,则甲、丁一人优秀一人良好,乙看到丙的结果则知道自己的结果,丁看到甲的结果则知道自己的结果.
故选:D.
5.B
【分析】
假设涛涛说谎,通过矛盾说明假设不成立即可得出结论.
【详解】
如果涛涛说谎,则毛毛没有说谎,即可可说谎,与只有一个小孩说谎矛盾,所以涛涛没有说谎,即玻璃是可可打破的.
故选:B.
6.B
【分析】
符合三段论:大前提,小前提,结论,所以是演绎推理.
【详解】
在推理的过程中:一切金属都能导电,是大前提,
铁是金属,是小前提,
所以铁能导电,是结论,
故是演绎推理,
故选:B
7.C
【分析】
根据题意,将直接代入,即可求出结果.
【详解】
用数学归纳法证明:,
在验证时,
令代入左边的代数式,得到左边.
故选:C
8.B
【分析】
写出和时的两式,然后比较可得.
【详解】
时等式为,
时等式为,
当时,等式左端应在的基础上加上,
故选:B.
【点睛】
本题考查数学归纳法,数学归纳法的关键、难点就在于用的假设结论证明的的结论,因此观察出与之间式子的关系至关重要.
9.A
【分析】
将命题的结论否定可得出结果.
【详解】
“方程至少有一个实根”的否定为“方程没有实根”.
因此,用反证法证明命题“设、为实数,则方程至少有一个实根”时,要做的假设是“方程没有实根”.
故选:A.
【点睛】
本题考查反证法,意在考查学生对反证法的理解,属于基础题.
10.B
【分析】
根据演绎推理的形式即可判断.
【详解】
大前提的形式: “鹅吃白菜”,不是全称命题,大前提本身正确,
小前提“参议员先生也吃白菜”本身也正确,但是不是大前提下的特殊情况,
鹅与人不能类比,
不符合三段论推理形式,推理形式错误.
故选:B
【点睛】
本题考查了知识点是演绎推理的基本方法,属于基础题.
11.B
【分析】
根据题目所给等式,归纳出正确结论.
【详解】
根据题目所给等式可知:,,.
故选:B
【点睛】
本小题主要考查合情推理,属于基础题.
12.C
【分析】
由于原不等式的等价于,再两边同时平方,即可得出答案.
【详解】
解:根据题意,欲证,
则需证,
只需证.
故选:C.
【点睛】
本题考查利用分析法证明不等式,体现转化思想,属于基础题.
13.
【分析】
在等式中令可得结果.
【详解】
由题知等式的左边有项,右边有项,且,因此第一步应验证时的等式,此时左边,右边,
故答案为:.
14.任意,
【分析】
由特称命题的否定可得解.
【详解】
反证法即为先假设命题的否定成立,及应先假设:任意,.
故答案为:任意,.
15.
【分析】
利用反证法即可得出结论
【详解】
假如说的是假话,则说的也是假话,不成立;
假如说的是假话,即没有写对,又没有写对,故写对了;
假如说的是假话,即写对了,则说的也是假话,不成立.
故说假话的同学是.
故答案为:B
【点睛】
此题考查简单的合情推理,考查学生分析解决问题的能力,属于基础题
16.
【分析】
根据表达式的规律即可猜想结论.
【详解】
解:由a>0,b>0,a+b=1,
一定有ab+≥4+,(ab)2+()2≥42+成立,
可以猜想:,
故答案为:.
【点睛】
本题考查了归纳推理的问题,关键找到规律,属于基础题.
17.证明见解析.
【分析】
利用题意,由分析法,原问题等价于,结合题意进行计算即可证得结论.
【详解】
证明:要证
只需证
只需证
只需证
只需证
因为成立,
所以.
【点睛】
本题考查分析法证明不等式,考查学生的逻辑推理能力,是一道容易题.
18.(1),,,(2)猜想
【分析】
(1)由数列递推式运算即可得解;重点考查了归纳推理能力,
(2)由前面有限项归纳通项公式即可得解.
【详解】
解:(1)由数列第一项,且,
则,,,
即,,,
(2)由,,,
猜想这个数列的通项公式为.
【点睛】
本题考查了数列递推式的运算,重点考查了归纳推理能力,属基础题.
19.(1),,,,;(2)见解析.
【分析】
(1)先求出的值,分析规律,再归纳出通项公式即可;
(2)将等比数列的定义作为大前提,然后将归纳得通项公式作为小前提,数列是等比数列则为结论.
【详解】
解:(1)由,
当时,,解得:,
当时,,解得:,
当时,,解得:,
由此归纳推理得:,.
(2)大前提:在数列中,若,是非零常数,则是等比数列;
小前提:在数列中,,;
结论:数列是等比数列.
【点睛】
本题考查了归纳推理,重点考查了三段论,属基础题.
20.(1),;(2),证明见解析.
【分析】
(1)依据递推关系可求、.
(2)根据(1)可猜测,按照数学归纳法的基本步骤证明即可.
【详解】
(1),;
(2)猜想数列通项公式,证明如下:
当时,,,所以成立;
假设时成立,即 ,
当时, ,
∴时,成立,
综上,由①②得: .
【点睛】
由数列的前若干项和递推关系可猜测数列的通项,然后再用数学归纳法去证明,注意数学归纳法有三个部分即归纳的起点、归纳假设和归纳证明,注意归纳证明的推理过程必须用到归纳假设.
21.(1)详见解析;
(2)详见解析;
(3).
【分析】
(1)对不等式分别使用基本不等式即可证明出;
(2)对不等式分别使用基本不等式即可证明出
;
(3)根据(1)(2)不等式的结构特征直接写出一般推广结论.
【详解】
(1)(当且仅当=1时取等号);
(2)(当且仅当时取等号);
(3)推广:已知,,…,则(当且仅当时取等号);
【点睛】
本题考查了基本不等式的应用与推广,考查了类比推理的能力.
22.(1) f(2)=5,f(3)=13,f(4)=25,f(5)=25+4×4=41.f(n)=2n2-2n+1.
(2)略
【解析】
本试题主要是考查了数列的归纳猜想思想的运用,根据前几项.来猜想并运用数学归纳法加以证明.
(1)结合题目中的 递推关系式可知前几项的值,并猜想结论.
(2)分为两步骤进行,先证明n取第一个值时成立,再假设n=k时成立,证明n=k+1时也成立即可.
解: (1)∵f(1)=1,f(2)=5,f(3)=13,f(4)=25,∴f(5)=25+4×4=41.
∵f(2)-f(1)=4=4×1,f(3)-f(2)=8=4×2,f(4)-f(3)=12=4×3,f(5)-f(4)=16=4×4,
由上式规律得出f(n+1)-f(n)=4n. ∴f(n)-f(n-1)=4(n-1),f(n-1)-f(n-2)=4·(n-2),
f(n-2)-f(n-3)=4·(n-3),…
f(2)-f(1)=4×1,
∴f(n)-f(1)=4[(n-1)+(n-2)+…+2+1]=2(n-1)·n,∴f(n)=2n2-2n+1(n≥2),
又n=1时,f(1)也适合f(n).
∴f(n)=2n2-2n+1. --------6分
---------------12分
