2020—2021学年湘教版数学八年 下册 第二章 四边形 单元测试(Word版含答案)
文档属性
| 名称 | 2020—2021学年湘教版数学八年 下册 第二章 四边形 单元测试(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 190.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-20 00:00:00 | ||
图片预览




文档简介
第2章 四边形
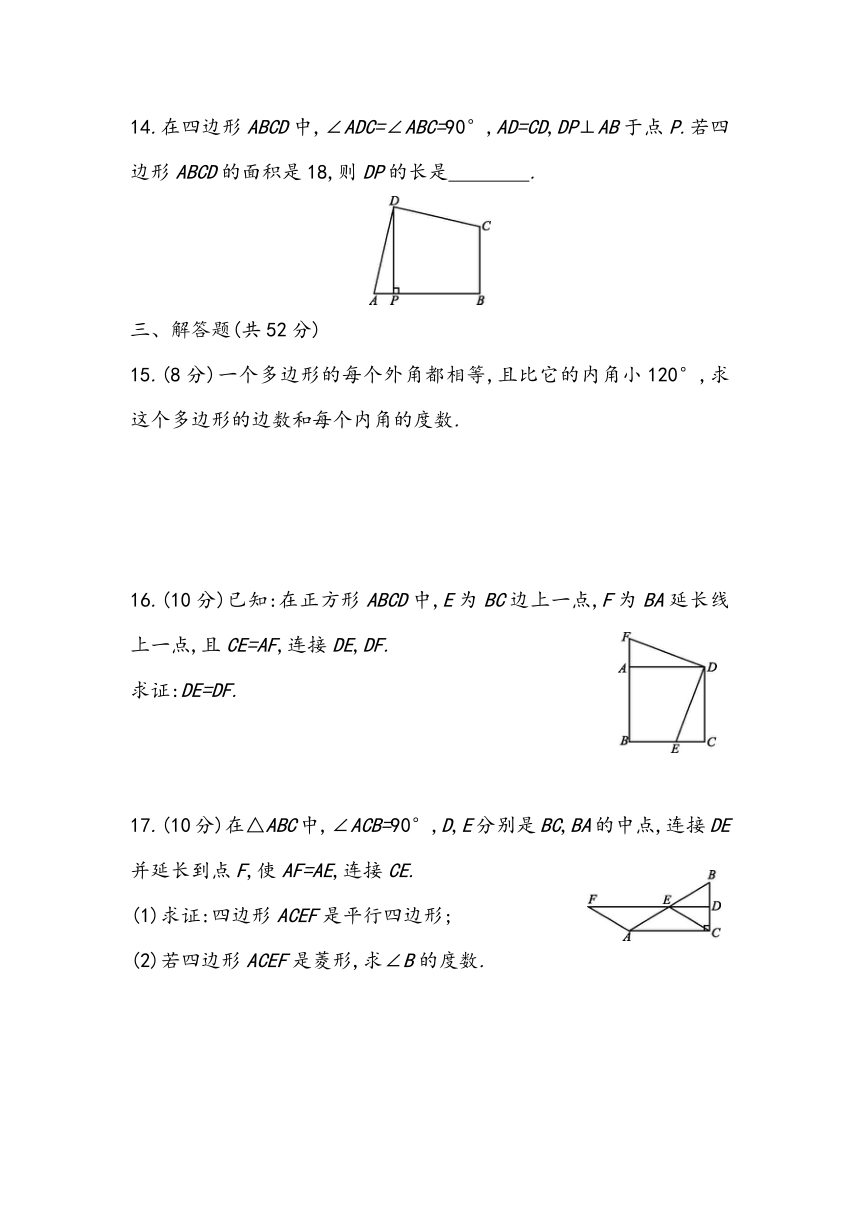
单元测试
一、选择题(每小题3分,共24分)
1.下列图形中,是中心对称图形的是
( )
2.若一个多边形的每个外角都等于45°,则这个多边形的边数为
( )
A.8
B.7
C.6
D.5
3.在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为
( )
A.24
B.18
C.12
D.9
4.已知四边形ABCD,下列说法正确的是
( )
A.当AD=BC,AB∥DC时,四边形ABCD是平行四边形
B.当AD=BC,AB=DC时,四边形ABCD是平行四边形
C.当AC=BD,AC平分BD时,四边形ABCD是矩形
D.当AC=BD,AC⊥BD时,四边形ABCD是正方形
5.在菱形ABCD中,AC=8,BD=6,则△ABC的周长是( )
A.14
B.16
C.18
D.20
6.在四边形ABCD中,AB=CD,E,F,G分别为AD,BD,BC的中点.若∠FEG=25°,∠ABD=20°,则∠BDC的度数为
( )
A.45°
B.50°
C.70°
D.65°
7.在矩形ABCD中,AB=3,将△ABD沿对角线BD对折,得到△EBD,DE与BC交于点F,∠ADB=30°,则EF的长为
( )
A.
B.2
C.3
D.3
8.正方形ABCD的对角线相交于点O,正方形EFGO绕点O旋转,则两正方形重叠部分的面积
( )
A.由小变大
B.由大变小
C.始终不变
D.先由大变小,然后又由小变大
二、填空题(每小题4分,共24分)
9.正十边形的每个外角都等于 °.?
10.在?ABCD中,BE平分∠ABC,BC=6,DE=2,
则?ABCD的周长为 .?
11.在?ABCD中,对角线AC,BD相交于点O,请你添加一个适当的条件,使?ABCD成为矩形,则你添加的条件是 .?
12.已知菱形ABCD的面积为24
cm2.若对角线AC=6
cm,则这个菱形的边长为
cm.?
13.矩形ABCD的对角线AC=8
cm,∠AOD=120°,
则AB的长为 .?
14.在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是18,则DP的长是 .?
三、解答题(共52分)
15.(8分)一个多边形的每个外角都相等,且比它的内角小120°,求这个多边形的边数和每个内角的度数.
16.(10分)已知:在正方形ABCD中,E为BC边上一点,F为BA延长线上一点,且CE=AF,连接DE,DF.
求证:DE=DF.
17.(10分)在△ABC中,∠ACB=90°,D,E分别是BC,BA的中点,连接DE并延长到点F,使AF=AE,连接CE.
(1)求证:四边形ACEF是平行四边形;
(2)若四边形ACEF是菱形,求∠B的度数.
18.(12分)在△ABC中,BD平分∠ABC,AE⊥BD于点O,交BC于点E,AD∥BC,连接ED.
(1)求证:AO=EO;
(2)当△ABC满足什么条件时四边形ABED是正方形?请说明理由.
19.(12分)四边形ABCD四条边上的中点分别为E,F,G,H,顺次连接EF,FG,GH,HE,得到四边形EFGH.
(1)四边形EFGH的形状是 ,证明你的结论;?
(2)当四边形ABCD的对角线 时,四边形EFGH是矩形;?
(3)你学过的哪种特殊四边形的中点四边形是矩形(不是正方形): .?
1.C
2.A [解析]
∵多边形的每一个外角都是45°,
∴这个多边形的边数是=8.故选A.
3.A [解析]
∵E是AC的中点,
且EF∥BC,交AB于点F,
∴EF是△ABC的中位线,∴EF=BC,
∴BC=6,∴菱形ABCD的周长=4×6=24.
故选A.
4.B
5.C [解析]
∵在菱形ABCD中,AC=8,BD=6,
∴AB=BC,∠AOB=90°,AO=4,BO=3,
∴BC=AB==5,
∴△ABC的周长=AB+BC+AC=5+5+8=18.
6.C [解析]
∵E,F分别为AD,BD的中点,∴EF=AB,EF∥AB,∴∠EFD=∠ABD=20°.设EG交BD于点H,∴∠FHG=25°+20°=45°,同理,FG=CD,FG∥CD.又∵AB=CD,∴EF=FG,∴∠FGE=∠FEG=25°,∴∠BFG=45°+25°=70°.∵FG∥CD,∴∠BDC=∠BFG=70°.故选C.
7.A
8.C [解析]
∵四边形ABCD和四边形EFGO都是正方形,
∴OB=OC,∠OBC=∠OCD=45°,∠BOC=∠EOG=90°,
∴∠BON=∠MOC.
∴△OBN≌△OCM(ASA),
∴重叠部分的面积总等于△BOC的面积.
故选C.
9.36
10.20 [解析]
∵四边形ABCD为平行四边形,
∴AE∥BC,AD=BC,AB=DC,
∴∠AEB=∠EBC.
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE.
∵AE+DE=AD=BC=6,
∴AE+2=6,∴AE=4,
∴AB=AE=CD=4,
∴?ABCD的周长=4+4+6+6=20.
11.AC=BD(不唯一) [解析]
对角线相等的平行四边形是矩形.
12.5
13.4
cm [解析]
∵四边形ABCD是矩形,
∴OA=AC,OB=BD,BD=AC=8
cm,
∴OA=OB=4
cm.
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=4
cm.
14.3 [解析]
如图,过点D作DE⊥BC交BC的延长线于点E.∵∠ABC=90°,DP⊥AB,∴四边形DPBE是矩形,∴∠PDE=90°,即∠CDE+∠CDP=90°.∵∠ADC=90°,∴∠ADP+∠CDP=90°,∴∠ADP=∠CDE.
在△ADP和△CDE中,
∴△ADP≌△CDE(AAS),
∴DE=DP,四边形ABCD的面积=四边形DPBE的面积=18,
∴矩形DPBE是正方形,
∴DP==3.
15.解:设每个内角的度数为n°,则每个外角的度数为n°-120°.
由n+(n-120)=180,得n=150,
即每个内角的度数为150°,
则每个外角的度数为30°.
因为360÷30=12,
所以这个多边形的边数为12,每个内角的度数为150°.
16.证明:∵四边形ABCD是正方形,
∴AD=CD,∠DAB=∠C=90°,
∴∠FAD=180°-∠DAB=90°,
∴∠C=∠FAD.
在△DCE和△DAF中,
∴△DCE≌△DAF(SAS),
∴DE=DF.
17.解:(1)证明:如图,∵∠ACB=90°,E是BA的中点,
∴CE=AE=BE.
∵AF=AE,∴AF=CE.
在△BEC中,∵BE=CE且D是BC的中点,
∴∠1=∠2.
∵AF=AE,∴∠F=∠3.
又∵∠1=∠3,∴∠2=∠F,
∴CE∥AF.
又∵CE=AF,
∴四边形ACEF是平行四边形.
(2)∵四边形ACEF是菱形,
∴AC=CE.
由(1)知AE=CE,∴AC=CE=AE,
∴△AEC是等边三角形,
∴∠CAE=60°,
∴在Rt△ABC中,∠B=90°-∠CAE=90°-60°=30°.
18.解:(1)证明:∵AD∥BC,
∴∠CBD=∠ADB.
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD.
又∵AE⊥BD,
∴BO=DO.
又∵∠AOD=∠EOB,
∴△AOD≌△EOB,∴AO=EO.
(2)当△ABC满足∠ABC=90°时,四边形ABED是正方形.理由:
由(1),得BO=DO,AO=EO,
∴四边形ABED是平行四边形.
又∵AE⊥BD,∴四边形ABED是菱形,
∴当∠ABC=90°时,菱形ABED是正方形.
19.解:(1)平行四边形
证明:连接BD.
∵E,H分别是AB,AD的中点,
∴EH∥BD,EH=BD.
同理FG∥BD,FG=BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.
(2)互相垂直
(3)菱形
单元测试
一、选择题(每小题3分,共24分)
1.下列图形中,是中心对称图形的是
( )
2.若一个多边形的每个外角都等于45°,则这个多边形的边数为
( )
A.8
B.7
C.6
D.5
3.在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为
( )
A.24
B.18
C.12
D.9
4.已知四边形ABCD,下列说法正确的是
( )
A.当AD=BC,AB∥DC时,四边形ABCD是平行四边形
B.当AD=BC,AB=DC时,四边形ABCD是平行四边形
C.当AC=BD,AC平分BD时,四边形ABCD是矩形
D.当AC=BD,AC⊥BD时,四边形ABCD是正方形
5.在菱形ABCD中,AC=8,BD=6,则△ABC的周长是( )
A.14
B.16
C.18
D.20
6.在四边形ABCD中,AB=CD,E,F,G分别为AD,BD,BC的中点.若∠FEG=25°,∠ABD=20°,则∠BDC的度数为
( )
A.45°
B.50°
C.70°
D.65°
7.在矩形ABCD中,AB=3,将△ABD沿对角线BD对折,得到△EBD,DE与BC交于点F,∠ADB=30°,则EF的长为
( )
A.
B.2
C.3
D.3
8.正方形ABCD的对角线相交于点O,正方形EFGO绕点O旋转,则两正方形重叠部分的面积
( )
A.由小变大
B.由大变小
C.始终不变
D.先由大变小,然后又由小变大
二、填空题(每小题4分,共24分)
9.正十边形的每个外角都等于 °.?
10.在?ABCD中,BE平分∠ABC,BC=6,DE=2,
则?ABCD的周长为 .?
11.在?ABCD中,对角线AC,BD相交于点O,请你添加一个适当的条件,使?ABCD成为矩形,则你添加的条件是 .?
12.已知菱形ABCD的面积为24
cm2.若对角线AC=6
cm,则这个菱形的边长为
cm.?
13.矩形ABCD的对角线AC=8
cm,∠AOD=120°,
则AB的长为 .?
14.在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是18,则DP的长是 .?
三、解答题(共52分)
15.(8分)一个多边形的每个外角都相等,且比它的内角小120°,求这个多边形的边数和每个内角的度数.
16.(10分)已知:在正方形ABCD中,E为BC边上一点,F为BA延长线上一点,且CE=AF,连接DE,DF.
求证:DE=DF.
17.(10分)在△ABC中,∠ACB=90°,D,E分别是BC,BA的中点,连接DE并延长到点F,使AF=AE,连接CE.
(1)求证:四边形ACEF是平行四边形;
(2)若四边形ACEF是菱形,求∠B的度数.
18.(12分)在△ABC中,BD平分∠ABC,AE⊥BD于点O,交BC于点E,AD∥BC,连接ED.
(1)求证:AO=EO;
(2)当△ABC满足什么条件时四边形ABED是正方形?请说明理由.
19.(12分)四边形ABCD四条边上的中点分别为E,F,G,H,顺次连接EF,FG,GH,HE,得到四边形EFGH.
(1)四边形EFGH的形状是 ,证明你的结论;?
(2)当四边形ABCD的对角线 时,四边形EFGH是矩形;?
(3)你学过的哪种特殊四边形的中点四边形是矩形(不是正方形): .?
1.C
2.A [解析]
∵多边形的每一个外角都是45°,
∴这个多边形的边数是=8.故选A.
3.A [解析]
∵E是AC的中点,
且EF∥BC,交AB于点F,
∴EF是△ABC的中位线,∴EF=BC,
∴BC=6,∴菱形ABCD的周长=4×6=24.
故选A.
4.B
5.C [解析]
∵在菱形ABCD中,AC=8,BD=6,
∴AB=BC,∠AOB=90°,AO=4,BO=3,
∴BC=AB==5,
∴△ABC的周长=AB+BC+AC=5+5+8=18.
6.C [解析]
∵E,F分别为AD,BD的中点,∴EF=AB,EF∥AB,∴∠EFD=∠ABD=20°.设EG交BD于点H,∴∠FHG=25°+20°=45°,同理,FG=CD,FG∥CD.又∵AB=CD,∴EF=FG,∴∠FGE=∠FEG=25°,∴∠BFG=45°+25°=70°.∵FG∥CD,∴∠BDC=∠BFG=70°.故选C.
7.A
8.C [解析]
∵四边形ABCD和四边形EFGO都是正方形,
∴OB=OC,∠OBC=∠OCD=45°,∠BOC=∠EOG=90°,
∴∠BON=∠MOC.
∴△OBN≌△OCM(ASA),
∴重叠部分的面积总等于△BOC的面积.
故选C.
9.36
10.20 [解析]
∵四边形ABCD为平行四边形,
∴AE∥BC,AD=BC,AB=DC,
∴∠AEB=∠EBC.
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE.
∵AE+DE=AD=BC=6,
∴AE+2=6,∴AE=4,
∴AB=AE=CD=4,
∴?ABCD的周长=4+4+6+6=20.
11.AC=BD(不唯一) [解析]
对角线相等的平行四边形是矩形.
12.5
13.4
cm [解析]
∵四边形ABCD是矩形,
∴OA=AC,OB=BD,BD=AC=8
cm,
∴OA=OB=4
cm.
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=4
cm.
14.3 [解析]
如图,过点D作DE⊥BC交BC的延长线于点E.∵∠ABC=90°,DP⊥AB,∴四边形DPBE是矩形,∴∠PDE=90°,即∠CDE+∠CDP=90°.∵∠ADC=90°,∴∠ADP+∠CDP=90°,∴∠ADP=∠CDE.
在△ADP和△CDE中,
∴△ADP≌△CDE(AAS),
∴DE=DP,四边形ABCD的面积=四边形DPBE的面积=18,
∴矩形DPBE是正方形,
∴DP==3.
15.解:设每个内角的度数为n°,则每个外角的度数为n°-120°.
由n+(n-120)=180,得n=150,
即每个内角的度数为150°,
则每个外角的度数为30°.
因为360÷30=12,
所以这个多边形的边数为12,每个内角的度数为150°.
16.证明:∵四边形ABCD是正方形,
∴AD=CD,∠DAB=∠C=90°,
∴∠FAD=180°-∠DAB=90°,
∴∠C=∠FAD.
在△DCE和△DAF中,
∴△DCE≌△DAF(SAS),
∴DE=DF.
17.解:(1)证明:如图,∵∠ACB=90°,E是BA的中点,
∴CE=AE=BE.
∵AF=AE,∴AF=CE.
在△BEC中,∵BE=CE且D是BC的中点,
∴∠1=∠2.
∵AF=AE,∴∠F=∠3.
又∵∠1=∠3,∴∠2=∠F,
∴CE∥AF.
又∵CE=AF,
∴四边形ACEF是平行四边形.
(2)∵四边形ACEF是菱形,
∴AC=CE.
由(1)知AE=CE,∴AC=CE=AE,
∴△AEC是等边三角形,
∴∠CAE=60°,
∴在Rt△ABC中,∠B=90°-∠CAE=90°-60°=30°.
18.解:(1)证明:∵AD∥BC,
∴∠CBD=∠ADB.
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD.
又∵AE⊥BD,
∴BO=DO.
又∵∠AOD=∠EOB,
∴△AOD≌△EOB,∴AO=EO.
(2)当△ABC满足∠ABC=90°时,四边形ABED是正方形.理由:
由(1),得BO=DO,AO=EO,
∴四边形ABED是平行四边形.
又∵AE⊥BD,∴四边形ABED是菱形,
∴当∠ABC=90°时,菱形ABED是正方形.
19.解:(1)平行四边形
证明:连接BD.
∵E,H分别是AB,AD的中点,
∴EH∥BD,EH=BD.
同理FG∥BD,FG=BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.
(2)互相垂直
(3)菱形
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
