第4章相交线与平行线单元复习湖南省株洲市外国语学校2020-2021学年 湘教版七年级下册(word版含解析)
文档属性
| 名称 | 第4章相交线与平行线单元复习湖南省株洲市外国语学校2020-2021学年 湘教版七年级下册(word版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 135.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-19 00:00:00 | ||
图片预览





文档简介
湖南省株洲市外国语学校2021湘教版七年级下
----------相交线与平行线单元复习
一、
选择题
?1.
下列说法中正确的个数有(????????)
①两条直线被第三条直线所截,内错角相等;
②在同一平面内不重合的两条直线有平行、相交和垂直三种位置关系;
③直线外一点到这条直线的垂线段的长度叫做点到直线的距离;
④在同一平面内,垂直于同一条直线的两条直线互相平行.
A.个
B.个
C.个
D.个
?2.
如果和是同旁内角,且,那么为(
)
A.
B.
C.
D.不能确定
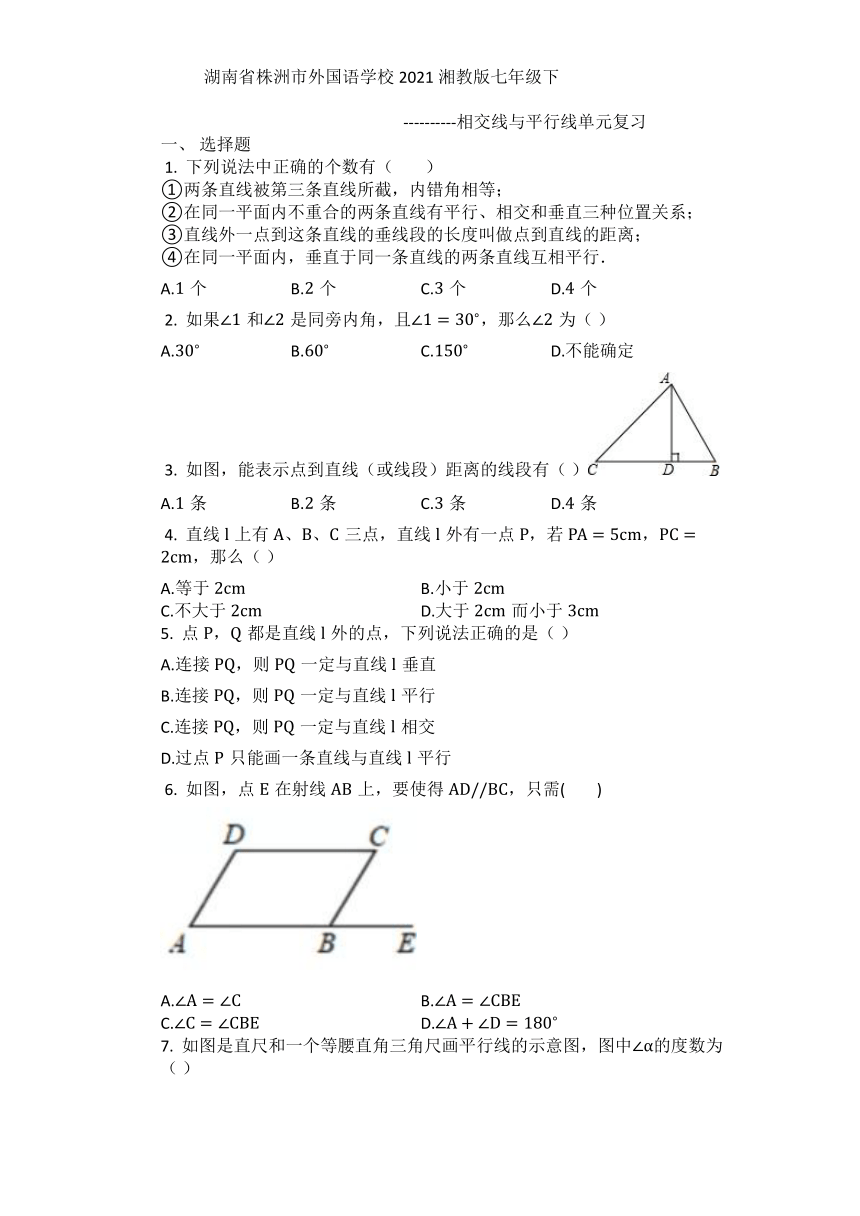
?3.
如图,能表示点到直线(或线段)距离的线段有(
)
A.条
B.条
C.条
D.条
?4.
直线上有、、三点,直线外有一点,若,,那么(
)
A.等于
B.小于
C.不大于
D.大于而小于
5.
点,都是直线外的点,下列说法正确的是(
)
A.连接,则一定与直线垂直
B.连接,则一定与直线平行
C.连接,则一定与直线相交
D.过点只能画一条直线与直线平行
?6.
如图,点在射线上,要使得,只需(?
?
?
?
)
A.
B.
C.
D.
7.
如图是直尺和一个等腰直角三角尺画平行线的示意图,图中的度数为(
)
A.
B.
C.
D.
?8.
如图,直线,将含有角的三角形板的直角顶点放在直线上,若,则的度数为(?
?
?
?
)
A.
B.
C.
D.
?9.
下列说法中不正确的是(
)
A.平移不改变图形的形状和大小
B.平移中,图形上每个点移动的距离可以不同
C.经过平移,图形的对应线段、对应角分别相等
D.经过平移,图形对应点的连结线段平行且相等
?10.
如图,是正六边形的中心,下列图形中可由三角形平移得到的是(
)
A.三角形
B.三角形
C.三角形
D.三角形
?11.
将直线向右平移个单位,在向上平移个单位后,所得的直线的表达式为(?
?
?
?
?
)
A.
B.
C.
D.
?12.
如图,若,则、、之间的关系为(
)
A.=
B.=
C.=
D.=
?13.
如图是一汽车探照灯纵剖面,从位于点的灯泡发出的两束光线,经过灯碗反射以后平行射出,如果,,则的度数是(
)
A.
B.
C.
D.
二、
填空题
14.
若直线,相交于,与的和为,则的度数为________度.
?15.
如图,计划把河水引到水池中,先引,垂足为,然后沿开渠,能使所开的渠道最短,这样设计的依据是________.
?16.
平行线、之间的距离为,若点是直线上一点,点是直线上一点,则________.(填“、、、或”)
?17.
如图,点在直线上移动,,是直线上的两个定点,且直线;对于下列各值:①点到直线的距离;②的周长;③的面积;④的大小.其中不会随点的移动而变化的是________.
三、
解答题
18.
如图,已知,,,求证:.
证明:∵
,(已知),
∴
(垂直的定义),
∴
(?
?
?
?
),
∴
________(?
?
?
?
).
∵
(已知),
∴
________(等量代换),
∴
(?
?
?
?
),
∴
________(?
?
?
?
).
∵
(已知),
∴
(?
?
?
?
),
∴
(?
?
?
?
),
∴
(?
?
?
?
).
?19.
如图,在边长为个单位长度的小正方形组成的网格中.
把进行平移,得到,使点与对应,请在网格中画出;
线段与线段的位置关系与数量关系分别是________.
?
20.
如图,已知、、=.
(1)________=________.
(2)若平分,交于点,且=,求的度数.
?
21.
如图所示,已知,直线分别交、于点,,试探究两平行直线被第三条直线所截形成的同位角、内错角、同旁内角的角平分线的关系.
如图①,、分别平分,试说明:.
如图②,、分别平分,试说明:.
如图③,、分别平分,试说明:.
参考答案与试题解析
一、
选择题
1.
【答案】
B
【解答】
解:两直线平行,内错角相等,故错误;
在同一平面内不重合的两条直线有平行、相交二种位置关系,故错误;
直线外一点到这条直线的垂线段的长度叫做点到直线的距离,故正确;
在同一平面内,垂直于同一条直线的两条直线,根据同位角相等可得两直线平行,故正确.
故选.
2.
【答案】
D
【解答】
解:同旁内角只是一种位置关系,两直线平行时同旁内角互补,不平行时无法确定同旁内角的大小关系.
故选:.
3.
【答案】
C
【解答】
解:是到的距离,是到的距离,是到的距离,
故选:.
4.
【答案】
C
【解答】
解:∵
垂线段最短,其它线段的长度大于或等于,
故选.
5.
【答案】
D
【解答】
解:与直线可能平行,也可能相交,故、、,均错误;
过直线外一点有且只有一条直线与已知直线平行,故正确.
故选:.
6.
【答案】
B
【解答】
解:要,只需,
同位角相等,两直线平行.
故选.
7.
【答案】
B
【解答】
∵
是等腰直角三角形,
∴
==,
∵
,
∴
==,
8.
【答案】
B
【解答】
解:如图,过点作,
∵
直线,
∴
,
∴
,
∵
是有一个角是的直角三角板,
∴
,
∴
.
故选.
9.
【答案】
B
【解答】
解:根据平移只改变图形的位置,不改变图形的大小和形状知道错误.
故选.
10.
【答案】
C
【解答】
解:、方向发生了变化,不属于平移得到;故本选项错误;
、方向发生了变化,不属于平移得到,故本选项错误;
、属于平移得到;故本选项正确;
、方向发生了变化,不属于平移得到;故本选项错误.
故选.
11.
【答案】
A
【解答】
解:,
化简,得:,
故选.
12.
【答案】
C
【解答】
作.
∵
,,
∴
,
∴
=,==,
∴
=,
13.
【答案】
A
【解答】
解:过点作,
∵
,
∴
,
∴
,,
∴
.
故选.
二、
填空题
14.
【答案】
【解答】
解:若直线,相交于,
则,,
∵
周角,与的和为,
∴
则的度数为.
15.
【答案】
垂线段最短
【解答】
解:计划把河水引到水池中,先引,垂足为,然后沿开渠,能使所开的渠道最短,这样设计的依据是垂线段最短,
故答案为:垂线段最短.
16.
【答案】
【解答】
解:∵
,之间的距离是,
当直线时,,
当和直线不垂直时,,
即,
∴
,
故答案为:.
17.
【答案】
①③
【解答】
解:∵直线,
∴点到直线的距离不变;故①正确;
∵
,的长度随点的移动而变化,
∴
的周长会随点的移动而变化,故②错误;
∵点到直线的距离不变,的大小,
∴
的面积不变,故③正确;
直线,之间的距离不随点的移动而变化,
的大小随点的移动而变化,故④错误;
综上所述,不会随点的移动而变化的是①③.
故答案为:①③.
三、
解答题
18.
【答案】
解:∵
,(已知),
∴
(垂直的定义),
∴
(同位角相等,两直线平行),
∴
(两直线平行,内错角相等).
∵
(已知),
∴
(等量代换),
∴
(同位角相等,两直线平行),
∴
(两直线平行,同位角相等),
∵
(已知),
∴
(垂直的定义),
∴
(等量代换),
∴
(垂直的定义).
【解答】
解:∵
,(已知),
∴
(垂直的定义),
∴
(同位角相等,两直线平行),
∴
(两直线平行,内错角相等).
∵
(已知),
∴
(等量代换),
∴
(同位角相等,两直线平行),
∴
(两直线平行,同位角相等),
∵
(已知),
∴
(垂直的定义),
∴
(等量代换),
∴
(垂直的定义).
19.
【答案】
解:所作图形如图所示:
平行且相等
【解答】
解:所作图形如图所示:
由平移的性质可得,
线段与线段平行且相等.
故答案为:平行且相等.
20.
【答案】
,
∵
=,=,
∴
=,
∵
,=,
∵
平分,
∴
=,
∴
==.
【解答】
∵
,
∴
==,
∵
,
∴
==,
故答案为:,
∵
=,=,
∴
=,
∵
,=,
∵
平分,
∴
=,
∴
==.
21.
【答案】
解:,
(两直线平行,同位角相等),
∵
分别平分,
∴
,
(同位角相等,两直线平行),
两平行直线被第三条直线所截,同位角的角平分线互相平行.
,
∴
(两直线平行,内错角相等),
∵
分别平分,
∴
,
,
(内错角相等,两直线平行),
两平行直线被第三条直线所截,内错角的角平分线互相平行.
,
(两直线平行,同旁内角互补),
∵
分别平分,
,
,
,
.
(同位角相等,两直线平行),
两平行直线被第三条直线所截,同旁内角的角平分线互相垂直.
【解答】
解:,
(两直线平行,同位角相等),
∵
分别平分,
∴
,
(同位角相等,两直线平行),
两平行直线被第三条直线所截,同位角的角平分线互相平行.
,
∴
(两直线平行,内错角相等),
∵
分别平分,
∴
,
,
(内错角相等,两直线平行),
两平行直线被第三条直线所截,内错角的角平分线互相平行.
,
(两直线平行,同旁内角互补),
∵
分别平分,
,
,
,
.
(同位角相等,两直线平行),
两平行直线被第三条直线所截,同旁内角的角平分线互相垂直.
----------相交线与平行线单元复习
一、
选择题
?1.
下列说法中正确的个数有(????????)
①两条直线被第三条直线所截,内错角相等;
②在同一平面内不重合的两条直线有平行、相交和垂直三种位置关系;
③直线外一点到这条直线的垂线段的长度叫做点到直线的距离;
④在同一平面内,垂直于同一条直线的两条直线互相平行.
A.个
B.个
C.个
D.个
?2.
如果和是同旁内角,且,那么为(
)
A.
B.
C.
D.不能确定
?3.
如图,能表示点到直线(或线段)距离的线段有(
)
A.条
B.条
C.条
D.条
?4.
直线上有、、三点,直线外有一点,若,,那么(
)
A.等于
B.小于
C.不大于
D.大于而小于
5.
点,都是直线外的点,下列说法正确的是(
)
A.连接,则一定与直线垂直
B.连接,则一定与直线平行
C.连接,则一定与直线相交
D.过点只能画一条直线与直线平行
?6.
如图,点在射线上,要使得,只需(?
?
?
?
)
A.
B.
C.
D.
7.
如图是直尺和一个等腰直角三角尺画平行线的示意图,图中的度数为(
)
A.
B.
C.
D.
?8.
如图,直线,将含有角的三角形板的直角顶点放在直线上,若,则的度数为(?
?
?
?
)
A.
B.
C.
D.
?9.
下列说法中不正确的是(
)
A.平移不改变图形的形状和大小
B.平移中,图形上每个点移动的距离可以不同
C.经过平移,图形的对应线段、对应角分别相等
D.经过平移,图形对应点的连结线段平行且相等
?10.
如图,是正六边形的中心,下列图形中可由三角形平移得到的是(
)
A.三角形
B.三角形
C.三角形
D.三角形
?11.
将直线向右平移个单位,在向上平移个单位后,所得的直线的表达式为(?
?
?
?
?
)
A.
B.
C.
D.
?12.
如图,若,则、、之间的关系为(
)
A.=
B.=
C.=
D.=
?13.
如图是一汽车探照灯纵剖面,从位于点的灯泡发出的两束光线,经过灯碗反射以后平行射出,如果,,则的度数是(
)
A.
B.
C.
D.
二、
填空题
14.
若直线,相交于,与的和为,则的度数为________度.
?15.
如图,计划把河水引到水池中,先引,垂足为,然后沿开渠,能使所开的渠道最短,这样设计的依据是________.
?16.
平行线、之间的距离为,若点是直线上一点,点是直线上一点,则________.(填“、、、或”)
?17.
如图,点在直线上移动,,是直线上的两个定点,且直线;对于下列各值:①点到直线的距离;②的周长;③的面积;④的大小.其中不会随点的移动而变化的是________.
三、
解答题
18.
如图,已知,,,求证:.
证明:∵
,(已知),
∴
(垂直的定义),
∴
(?
?
?
?
),
∴
________(?
?
?
?
).
∵
(已知),
∴
________(等量代换),
∴
(?
?
?
?
),
∴
________(?
?
?
?
).
∵
(已知),
∴
(?
?
?
?
),
∴
(?
?
?
?
),
∴
(?
?
?
?
).
?19.
如图,在边长为个单位长度的小正方形组成的网格中.
把进行平移,得到,使点与对应,请在网格中画出;
线段与线段的位置关系与数量关系分别是________.
?
20.
如图,已知、、=.
(1)________=________.
(2)若平分,交于点,且=,求的度数.
?
21.
如图所示,已知,直线分别交、于点,,试探究两平行直线被第三条直线所截形成的同位角、内错角、同旁内角的角平分线的关系.
如图①,、分别平分,试说明:.
如图②,、分别平分,试说明:.
如图③,、分别平分,试说明:.
参考答案与试题解析
一、
选择题
1.
【答案】
B
【解答】
解:两直线平行,内错角相等,故错误;
在同一平面内不重合的两条直线有平行、相交二种位置关系,故错误;
直线外一点到这条直线的垂线段的长度叫做点到直线的距离,故正确;
在同一平面内,垂直于同一条直线的两条直线,根据同位角相等可得两直线平行,故正确.
故选.
2.
【答案】
D
【解答】
解:同旁内角只是一种位置关系,两直线平行时同旁内角互补,不平行时无法确定同旁内角的大小关系.
故选:.
3.
【答案】
C
【解答】
解:是到的距离,是到的距离,是到的距离,
故选:.
4.
【答案】
C
【解答】
解:∵
垂线段最短,其它线段的长度大于或等于,
故选.
5.
【答案】
D
【解答】
解:与直线可能平行,也可能相交,故、、,均错误;
过直线外一点有且只有一条直线与已知直线平行,故正确.
故选:.
6.
【答案】
B
【解答】
解:要,只需,
同位角相等,两直线平行.
故选.
7.
【答案】
B
【解答】
∵
是等腰直角三角形,
∴
==,
∵
,
∴
==,
8.
【答案】
B
【解答】
解:如图,过点作,
∵
直线,
∴
,
∴
,
∵
是有一个角是的直角三角板,
∴
,
∴
.
故选.
9.
【答案】
B
【解答】
解:根据平移只改变图形的位置,不改变图形的大小和形状知道错误.
故选.
10.
【答案】
C
【解答】
解:、方向发生了变化,不属于平移得到;故本选项错误;
、方向发生了变化,不属于平移得到,故本选项错误;
、属于平移得到;故本选项正确;
、方向发生了变化,不属于平移得到;故本选项错误.
故选.
11.
【答案】
A
【解答】
解:,
化简,得:,
故选.
12.
【答案】
C
【解答】
作.
∵
,,
∴
,
∴
=,==,
∴
=,
13.
【答案】
A
【解答】
解:过点作,
∵
,
∴
,
∴
,,
∴
.
故选.
二、
填空题
14.
【答案】
【解答】
解:若直线,相交于,
则,,
∵
周角,与的和为,
∴
则的度数为.
15.
【答案】
垂线段最短
【解答】
解:计划把河水引到水池中,先引,垂足为,然后沿开渠,能使所开的渠道最短,这样设计的依据是垂线段最短,
故答案为:垂线段最短.
16.
【答案】
【解答】
解:∵
,之间的距离是,
当直线时,,
当和直线不垂直时,,
即,
∴
,
故答案为:.
17.
【答案】
①③
【解答】
解:∵直线,
∴点到直线的距离不变;故①正确;
∵
,的长度随点的移动而变化,
∴
的周长会随点的移动而变化,故②错误;
∵点到直线的距离不变,的大小,
∴
的面积不变,故③正确;
直线,之间的距离不随点的移动而变化,
的大小随点的移动而变化,故④错误;
综上所述,不会随点的移动而变化的是①③.
故答案为:①③.
三、
解答题
18.
【答案】
解:∵
,(已知),
∴
(垂直的定义),
∴
(同位角相等,两直线平行),
∴
(两直线平行,内错角相等).
∵
(已知),
∴
(等量代换),
∴
(同位角相等,两直线平行),
∴
(两直线平行,同位角相等),
∵
(已知),
∴
(垂直的定义),
∴
(等量代换),
∴
(垂直的定义).
【解答】
解:∵
,(已知),
∴
(垂直的定义),
∴
(同位角相等,两直线平行),
∴
(两直线平行,内错角相等).
∵
(已知),
∴
(等量代换),
∴
(同位角相等,两直线平行),
∴
(两直线平行,同位角相等),
∵
(已知),
∴
(垂直的定义),
∴
(等量代换),
∴
(垂直的定义).
19.
【答案】
解:所作图形如图所示:
平行且相等
【解答】
解:所作图形如图所示:
由平移的性质可得,
线段与线段平行且相等.
故答案为:平行且相等.
20.
【答案】
,
∵
=,=,
∴
=,
∵
,=,
∵
平分,
∴
=,
∴
==.
【解答】
∵
,
∴
==,
∵
,
∴
==,
故答案为:,
∵
=,=,
∴
=,
∵
,=,
∵
平分,
∴
=,
∴
==.
21.
【答案】
解:,
(两直线平行,同位角相等),
∵
分别平分,
∴
,
(同位角相等,两直线平行),
两平行直线被第三条直线所截,同位角的角平分线互相平行.
,
∴
(两直线平行,内错角相等),
∵
分别平分,
∴
,
,
(内错角相等,两直线平行),
两平行直线被第三条直线所截,内错角的角平分线互相平行.
,
(两直线平行,同旁内角互补),
∵
分别平分,
,
,
,
.
(同位角相等,两直线平行),
两平行直线被第三条直线所截,同旁内角的角平分线互相垂直.
【解答】
解:,
(两直线平行,同位角相等),
∵
分别平分,
∴
,
(同位角相等,两直线平行),
两平行直线被第三条直线所截,同位角的角平分线互相平行.
,
∴
(两直线平行,内错角相等),
∵
分别平分,
∴
,
,
(内错角相等,两直线平行),
两平行直线被第三条直线所截,内错角的角平分线互相平行.
,
(两直线平行,同旁内角互补),
∵
分别平分,
,
,
,
.
(同位角相等,两直线平行),
两平行直线被第三条直线所截,同旁内角的角平分线互相垂直.
