2020-2021学年湘教版八年级数学下册期末综合练习(Word版,附答案解析)
文档属性
| 名称 | 2020-2021学年湘教版八年级数学下册期末综合练习(Word版,附答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-19 11:51:38 | ||
图片预览



文档简介
八年级数学期末综合练习
一、单选题(每小题3分,共36分)
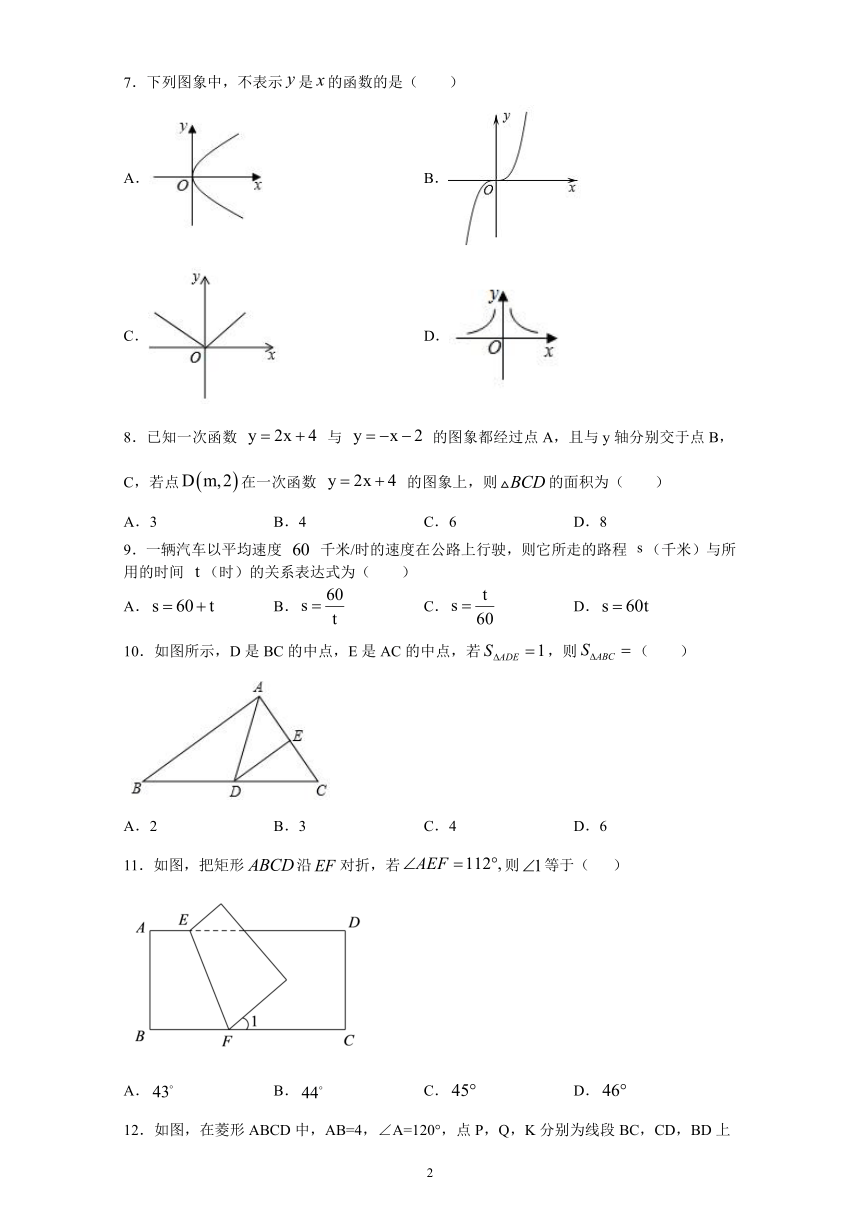
1.下列四种图形中,既是轴对称图形又是中心对称图形的是(
)
A.
B.
C.
D.
2.若过边形的一个顶点的所有对角线正好将该边形分成个三角形,则的值是(
)
A.
B.
C.
D.
3.如图,动点P从点(3,0)出发,沿所示方向运动,每当碰到长方形OABC的边时反弹,反弹后的路径与长方形的边的夹角为45°,第1次碰到长方形边上的点的坐标为(0,3)……第2018次碰到长方形边上的坐标为(
)
A.(1,4)
B.(5,0)
C.(8,3)
D.(7,4)
4.在平面直角坐标系xOy中,点A(﹣2,0),点B(0,3),点C在坐标轴上,若三角形ABC的面积为6,则符合题意的点C有(
)
A.1个
B.2个
C.3个
D.4个
5.已知一组数据:10,8,6,10,8,13,11,12,10,10,7,9,8,12,9,11,12,9,10,11,则频率为0.2的范围是(
)
A.6~7
B.10~11
C.8~9
D.12~13
6.如图所示,在中,,是的角平分线,,,垂足分别为E、F,①,;②;③若点为上任意一点,且,则的取值范围是;④.其中,正确的个数是(
)
A.1个
B.2个
C.3个
D.4个
7.下列图象中,不表示是的函数的是(
)
A.
B.
C.
D.
8.已知一次函数
与
的图象都经过点A,且与y轴分别交于点B,C,若点在一次函数
的图象上,则的面积为(
)
A.3
B.4
C.6
D.8
9.一辆汽车以平均速度
千米/时的速度在公路上行驶,则它所走的路程
(千米)与所用的时间
(时)的关系表达式为(
)
A.
B.
C.
D.
10.如图所示,D是BC的中点,E是AC的中点,若,则(
)
A.2
B.3
C.4
D.6
11.如图,把矩形沿对折,若则等于(
)
A.
B.
C.
D.
12.如图,在菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
A.2
B.2
C.4
D.2+2
二、填空题(每小题3分,共24分)
13.如图,在Rt△ABC中,∠C=90°,D为BC上一点,连接AD,过D点作DE⊥AB,且DE=DC.若AB=5,AC=3,则EB=____.
14.将点P(﹣2,﹣3)向左平移3个长度单位,再向上平移2个长度单位得到点Q,则点Q的坐标是_____.
15.小欢为一组数据制作频数表,他了解到这组数据的最大值是40,最小值是16,准备分组时取组距为4,为了使数据不落在边界上,他应将这组数据分成__________组.
16.已知Q在直线上,且点Q到两坐标轴的距离相等,那么点Q的坐标为__________.
17.已知某直线经过点,且与两坐标轴围成的三角形的面积为2,则该直线的函数表达式是_________.
18.如图中阴影部分是由4个完全相同的正方形拼接而成,若要在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是中心对称图形,则这个正方形应该添加在________处.(填写区域对应的序号)
19.在△ABC中,
AD是BC边上的高线,CE
是AB边上的中线,CD=AE,且CE20.如图,将两条宽(宽指的是两平行线之间的距离)都是,使∠ABC=60°,则四边形ABCD的面积为_________.
三、解答题(本大题共60分)
21.(6分)如图,在平面直角坐标系中,的顶点坐标分别为.
(1)画出与关于x轴对称的图形;
(2)写出各个顶点的坐标;
(3)求的面积.
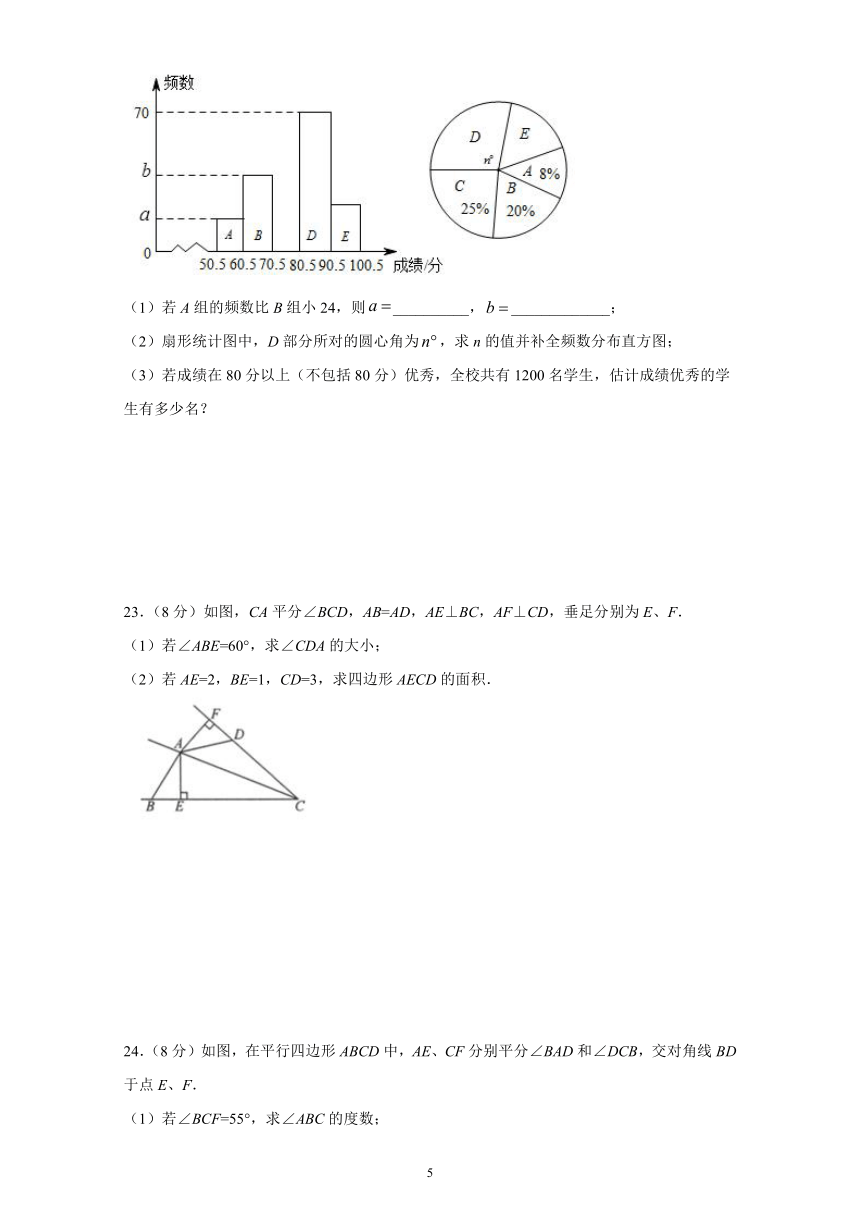
22.(8分)为了加强学生对新冠肺炎的预防意识,某校组织了学生参加新冠肺炎预防的知识竞赛,从中抽取了部分学生成绩(得分数取正整数,满分为100分)进行统计,绘制统计图如图(未完成),解答下列问题:
(1)若A组的频数比B组小24,则__________,_____________;
(2)扇形统计图中,D部分所对的圆心角为,求n的值并补全频数分布直方图;
(3)若成绩在80分以上(不包括80分)优秀,全校共有1200名学生,估计成绩优秀的学生有多少名?
23.(8分)如图,CA平分∠BCD,AB=AD,AE⊥BC,AF⊥CD,垂足分别为E、F.
(1)若∠ABE=60°,求∠CDA的大小;
(2)若AE=2,BE=1,CD=3,求四边形AECD的面积.
24.(8分)如图,在平行四边形ABCD中,AE、CF分别平分∠BAD和∠DCB,交对角线BD于点E、F.
(1)若∠BCF=55°,求∠ABC的度数;
(2)求证:BF=DE.
25.(10分)如图,在矩形ABCD中,∠BAD的平分线交BC于点E,EF⊥AD于点F,DG⊥AE于点G,DG与EF交于点O.
(1)求证:四边形ABEF是正方形;
(2)若AD=AE,求证:AB=AG;
(3)在(2)的条件下,已知AB=1,求OD的长.
26.(10分)如图,在平面直角坐标系中,O为坐标原点.的边在x轴上,A,C,B三点的坐标分别为,,,点P从B出发,以每秒2个单位的速度沿射线匀速运动,设点P运动时间为t秒.
(1)求直线的解析式和的边上的高线长;
(2)连接,写出的面积S与t的函数表达式;
(3)是否存在一点P,使是等腰三角形?若存在,请直接写出P点满足条件时,所有t的值;若不存在,请说明理由.
27.(10分)如图,在长方形中,,,为边上的一点,,动点从点出发,以每秒1个单位长度的速度沿着边向终点运动,连接,,设点运动的时间为秒.
(1)求的长;
(2)若为直角三角形,求的值;
(3)若点在的垂直平分线上,求的长.
参考答案
1.B
解:A、不是轴对称图形,是中心对称图形,不符合题意;
B、既是轴对称图形,也是中心对称,符合题意;
C、不是轴对称图形,是中心对称图形,不符合题意;
D、不是轴对称图形,是中心对称图形,不符合题意.
故选B.
2.D
解:经过边形的一个顶点的所有对角线把多边形分成个三角形,由题意,得,解得.
故选.
3.A
解:根据题意,如下图示:
通过上图观察可知,每碰撞6次回到始点.
∵2018÷6=336…2,
∴第2018次碰到长方形边上的点的坐标与第二次相同,即坐标为(1,4).
故选:A.
4.D
解:分两种情况:
①当C点在y轴上,设C(0,t),
∵三角形ABC的面积为6,
∴?|t﹣3|?2=6,
解得t=9或﹣3.
∴C点坐标为(0,﹣3),(0,9),
②当C点在x轴上,设C(m,0),
∵三角形ABC的面积为6,
∴?|m+2|?3=6,
解得m=2或﹣6.
∴C点坐标为(2,0),(﹣6,0),
综上所述,C点有4个,
故选:D.
5.D
解:A中,其频率=2÷20=0.1;
B中,其频率=6÷20=0.3;
C中,其频率=8÷20=0.4;
D中,其频率=4÷20=0.2.
故选D.
6.C
解:在中,
∵,是的角平分线,
∴,(三线合一),①正确;
∵是的角平分线,,,
∴,②正确;
∵,
∴DF=3,
∵点为上任意一点,且,
∴,③错误;
∵,
∴,
∵,,
∴,
∴,④正确;
即①②④正确;
故选:C.
7.A
解:A、根据图象知给自变量一个值,可能有2个函数值与其对应,故A选项不是函数,
B、根据图象知给自变量一个值,有且只有1个函数值与其对应,故B选项是函数,
C、根据图象知给自变量一个值,有且只有1个函数值与其对应,故C选项是函数,
D、根据图象知给自变量一个值,有且只有1个函数值与其对应,故D选项是函数,
故选:A.
8.A
解:根据题意,联立方程
解得
即点A的坐标为(-2,0)
又根据题意,可得点B(0,4),点C的坐标为(0,-2),点D的坐标为(-1,2)
中,BC=6,其高为点D的横坐标的长度,即为1,则
故答案为A.
9.D
解:根据路程=速度×时间得:汽车所走的路程s(千米)与所用的时间t(时)的关系表达式为:s=60t,故选D.
10.C
解:∵D是BC的中点,E是AC的中点,
∴△ADC的面积等于△ABC的面积的一半,△ADE的面积等于△ACD的面积的一半,
∴△ADE的面积等于△ABC的面积的四分之一,
又∵S△ADE=1,
∴S△ABC=4.
故答案为:4.
11.B
解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AEF+∠BFE=180°,
∵,
∴∠BFE=68°,
∴∠1=180°-2∠BFE=44°,
故选B.
12.B
解:作点P关于BD的对称点P′,作P′Q⊥CD交BD于K,交CD于Q,
∵AB=4,∠A=120°,
∴点P′到CD的距离为4×
=2,
∴PK+QK的最小值为2,
故选:B.
13.2
解:∵∠C=90°,DE⊥AB,
∴△AED和△ACD都是直角三角形,
在Rt△AED和Rt△ACD中,
DE=DC,AD=AD,
∴△AED≌△ACD(HL),
∴AE=AC=3,
∴BE=AB-AC=5-3=2.
故填:2.
14.(﹣5,﹣1)
解:根据题意,点Q的横坐标为:﹣2﹣3=﹣5;纵坐标为﹣3+2=﹣1;
即点Q的坐标是(﹣5,﹣1).
故答案为:(﹣5,﹣1).
15.7
解:∵这组数据的最大值是40,最小值是16,分组时取组距为4.
∴极差=40-16=24.
∵24÷4=6,
又∵数据不落在边界上,
∴这组数据的组数=6+1=7组.
故答案为:7
16.
解:(1)当点Q的坐标是(a,a)时,
a=-a+4,
解得a=2,
∴点Q的坐标是(2,2);
(2)当点Q的坐标是(b,-b)时,
-b=-b+4,
此方程无解.
∴点Q的坐标是(2,2).
故答案为:(2,2).
17.或
解:如下图:
∵点A(0、1)
∴OA=1
当直线与x轴相交于时,
∵直线与两坐标轴围成的三角形的面积为2,
∴,
解得,故(4、0)
设该直线的解析式为y=kx+1
将(4、0)代入得0=4k+1,解得
∴y=x+1
当直线与x轴相交于时,同理可求
将代入得0=-4k+1,解得
∴y=x+1
故该函数表达式为:y=x+1或y=x+1
故答案为
:y=x+1或y=x+1.
18.②
解:在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是中心对称图形,
这个正方形应该添加区域②处,
故答案为:②.
19.
解:∵AD是BC边上的高线,AD=6,AB=10,
∴∠D=90°,,
∵CE
是AB边上的中线,CD=AE,
∴,
取BD的中点F,连接CF,
∴EF为△ABD的中位线,
∴,EF//AD,
∴∠EFB=∠D=90°,
在Rt△BEF中,根据勾股定理,
,
∴DF=BD-BF=8-4=4,
∴CF=CD-DF=5-4=1,
在Rt△CEF中,根据勾股定理,
,
故答案为:.
20.
略
21.(1)见解析;(2);(3).
解:(1)如图,即为所求;
(2);
(3).
22.(1)16,40;(2)n=126,图见详解;(3)成绩优秀的学生有564名.
解:(1)由统计图及题意可得:抽取的总人数=24÷(20%-8%)=200(名),
∴(名),(名),
故答案为16,40;
(2)由图及(1)可得:
,
C组人数为:(人),
∴E组人数为:200-16-40-50-70=24(人),补全频数分布直方图如图所示:
(3)由(2)及题意可得:
(名);
答:成绩优秀的学生有564名.
23.(1)120°;(2)7
解:(1)平分,,,
,,
在Rt△AFD和Rt△AEB中,
,
∴Rt△AFD≌Rt△AEB(HL),
,
,
;
(2)∵Rt△AFD≌Rt△AEB,
,,
,
平分,
,
,,
,
在Rt△AFC和Rt△AEC中,
,
∴Rt△AFC≌Rt△AEC(HL),
,
四边形的面积.
24.(1)70°;(2)见解析.
(1)解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵CF平分∠DCB,
∴∠BCD=2∠BCF,
∵∠BCF=55°,
∴∠BCD=110°,
∴∠ABC=180°?110°=70°;
(2)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠BAD=∠DCB,
∴∠ABE=∠CDF,
∵AE,CF分别平分∠BAD和∠DCB,
∴∠BAE=∠BAD,∠DCF=∠DCB,
∴∠BAE=∠DCE,
∴△ABE≌△CDF(ASA),
∴BE=DF,
∴BE+EF=DF+EF,
即BF=DE.
25.(1)见解析;(2)见解析;(3)
(1)证明:∵四边形ABCD为矩形,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,
∴四边形ABEF是正方形;
(2)∵AE平分∠BAD,
∴∠DAG=∠BAE,
在△AGD和△ABE中,,
∴△AGD≌△ABE(AAS),
∴AB=AG;
(3)∵四边形ABEF是正方形,
∴AB=AF=1,
∵△AGD≌△ABE,
∴DG=AB=AF=AG=1,
∵AD=AE,
∴AD﹣AF=AE﹣AG,
即DF=EG,
在△DFO和△EGO中,,
∴△DFO≌△EGO(AAS),
∴FO=GO,FD=EG
∵∠DAE=∠AEF=45°,∠AFE=∠AGD=90°,
∴DF=FO=OG=EG,
∴DO=OF=OG,
∴DG=DO+OG=OG+OG=1,
∴OG==﹣1,
∴OD=(﹣1)=2﹣.
26.(1)直线AC的解析式为,AC边上的高为;(2);(3)存在,符合条件的t为1或1.5或6.5或.
解:(1)设直线AC的解析式为,将,代入得
,解得,
∴直线AC的解析式为,
∵,,,
∴,,,
∴,
设AC边上的高为h,
则,即,
解得,即AC边上的高为;
(2)当0≤t<2.5时,OP=5-2t,
∴△POA的面积,
当t>2.5时,OP=2t-5,
∴△POA的面积,
故;
(3)如图,当AP=AC时,
∵AO⊥BC,
∴PO=OC=3,BP=5-3=2,
∴此时t=1;
当PC=AC时,
∴BP=BC-PC=8-5=3或BP=BC+PC=8+5=13,
∴t=1.5或t=6.5;
当AP=PC时,
设PO=a,则CP=a+3,
∴,解得,
∴,
∴.
综上所述,存在,符合条件的t为1或1.5或6.5或.
27.(1)5;(2)7或;(3)
解:(1)根据题意知:,
∴,
∴的长为5;
(2)①当时,,,
∴;
②当时,过点作于点,
易得,.
在中,易得.
在中,,
∴,
解得:;
综上,当为7s或s时,为直角三角形;
(3)设.
∵在的垂直平分线上,
∴.
过点作于点.
易得.
在中,,
∴,
解得:,
∴的长为.
一、单选题(每小题3分,共36分)
1.下列四种图形中,既是轴对称图形又是中心对称图形的是(
)
A.
B.
C.
D.
2.若过边形的一个顶点的所有对角线正好将该边形分成个三角形,则的值是(
)
A.
B.
C.
D.
3.如图,动点P从点(3,0)出发,沿所示方向运动,每当碰到长方形OABC的边时反弹,反弹后的路径与长方形的边的夹角为45°,第1次碰到长方形边上的点的坐标为(0,3)……第2018次碰到长方形边上的坐标为(
)
A.(1,4)
B.(5,0)
C.(8,3)
D.(7,4)
4.在平面直角坐标系xOy中,点A(﹣2,0),点B(0,3),点C在坐标轴上,若三角形ABC的面积为6,则符合题意的点C有(
)
A.1个
B.2个
C.3个
D.4个
5.已知一组数据:10,8,6,10,8,13,11,12,10,10,7,9,8,12,9,11,12,9,10,11,则频率为0.2的范围是(
)
A.6~7
B.10~11
C.8~9
D.12~13
6.如图所示,在中,,是的角平分线,,,垂足分别为E、F,①,;②;③若点为上任意一点,且,则的取值范围是;④.其中,正确的个数是(
)
A.1个
B.2个
C.3个
D.4个
7.下列图象中,不表示是的函数的是(
)
A.
B.
C.
D.
8.已知一次函数
与
的图象都经过点A,且与y轴分别交于点B,C,若点在一次函数
的图象上,则的面积为(
)
A.3
B.4
C.6
D.8
9.一辆汽车以平均速度
千米/时的速度在公路上行驶,则它所走的路程
(千米)与所用的时间
(时)的关系表达式为(
)
A.
B.
C.
D.
10.如图所示,D是BC的中点,E是AC的中点,若,则(
)
A.2
B.3
C.4
D.6
11.如图,把矩形沿对折,若则等于(
)
A.
B.
C.
D.
12.如图,在菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
A.2
B.2
C.4
D.2+2
二、填空题(每小题3分,共24分)
13.如图,在Rt△ABC中,∠C=90°,D为BC上一点,连接AD,过D点作DE⊥AB,且DE=DC.若AB=5,AC=3,则EB=____.
14.将点P(﹣2,﹣3)向左平移3个长度单位,再向上平移2个长度单位得到点Q,则点Q的坐标是_____.
15.小欢为一组数据制作频数表,他了解到这组数据的最大值是40,最小值是16,准备分组时取组距为4,为了使数据不落在边界上,他应将这组数据分成__________组.
16.已知Q在直线上,且点Q到两坐标轴的距离相等,那么点Q的坐标为__________.
17.已知某直线经过点,且与两坐标轴围成的三角形的面积为2,则该直线的函数表达式是_________.
18.如图中阴影部分是由4个完全相同的正方形拼接而成,若要在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是中心对称图形,则这个正方形应该添加在________处.(填写区域对应的序号)
19.在△ABC中,
AD是BC边上的高线,CE
是AB边上的中线,CD=AE,且CE
三、解答题(本大题共60分)
21.(6分)如图,在平面直角坐标系中,的顶点坐标分别为.
(1)画出与关于x轴对称的图形;
(2)写出各个顶点的坐标;
(3)求的面积.
22.(8分)为了加强学生对新冠肺炎的预防意识,某校组织了学生参加新冠肺炎预防的知识竞赛,从中抽取了部分学生成绩(得分数取正整数,满分为100分)进行统计,绘制统计图如图(未完成),解答下列问题:
(1)若A组的频数比B组小24,则__________,_____________;
(2)扇形统计图中,D部分所对的圆心角为,求n的值并补全频数分布直方图;
(3)若成绩在80分以上(不包括80分)优秀,全校共有1200名学生,估计成绩优秀的学生有多少名?
23.(8分)如图,CA平分∠BCD,AB=AD,AE⊥BC,AF⊥CD,垂足分别为E、F.
(1)若∠ABE=60°,求∠CDA的大小;
(2)若AE=2,BE=1,CD=3,求四边形AECD的面积.
24.(8分)如图,在平行四边形ABCD中,AE、CF分别平分∠BAD和∠DCB,交对角线BD于点E、F.
(1)若∠BCF=55°,求∠ABC的度数;
(2)求证:BF=DE.
25.(10分)如图,在矩形ABCD中,∠BAD的平分线交BC于点E,EF⊥AD于点F,DG⊥AE于点G,DG与EF交于点O.
(1)求证:四边形ABEF是正方形;
(2)若AD=AE,求证:AB=AG;
(3)在(2)的条件下,已知AB=1,求OD的长.
26.(10分)如图,在平面直角坐标系中,O为坐标原点.的边在x轴上,A,C,B三点的坐标分别为,,,点P从B出发,以每秒2个单位的速度沿射线匀速运动,设点P运动时间为t秒.
(1)求直线的解析式和的边上的高线长;
(2)连接,写出的面积S与t的函数表达式;
(3)是否存在一点P,使是等腰三角形?若存在,请直接写出P点满足条件时,所有t的值;若不存在,请说明理由.
27.(10分)如图,在长方形中,,,为边上的一点,,动点从点出发,以每秒1个单位长度的速度沿着边向终点运动,连接,,设点运动的时间为秒.
(1)求的长;
(2)若为直角三角形,求的值;
(3)若点在的垂直平分线上,求的长.
参考答案
1.B
解:A、不是轴对称图形,是中心对称图形,不符合题意;
B、既是轴对称图形,也是中心对称,符合题意;
C、不是轴对称图形,是中心对称图形,不符合题意;
D、不是轴对称图形,是中心对称图形,不符合题意.
故选B.
2.D
解:经过边形的一个顶点的所有对角线把多边形分成个三角形,由题意,得,解得.
故选.
3.A
解:根据题意,如下图示:
通过上图观察可知,每碰撞6次回到始点.
∵2018÷6=336…2,
∴第2018次碰到长方形边上的点的坐标与第二次相同,即坐标为(1,4).
故选:A.
4.D
解:分两种情况:
①当C点在y轴上,设C(0,t),
∵三角形ABC的面积为6,
∴?|t﹣3|?2=6,
解得t=9或﹣3.
∴C点坐标为(0,﹣3),(0,9),
②当C点在x轴上,设C(m,0),
∵三角形ABC的面积为6,
∴?|m+2|?3=6,
解得m=2或﹣6.
∴C点坐标为(2,0),(﹣6,0),
综上所述,C点有4个,
故选:D.
5.D
解:A中,其频率=2÷20=0.1;
B中,其频率=6÷20=0.3;
C中,其频率=8÷20=0.4;
D中,其频率=4÷20=0.2.
故选D.
6.C
解:在中,
∵,是的角平分线,
∴,(三线合一),①正确;
∵是的角平分线,,,
∴,②正确;
∵,
∴DF=3,
∵点为上任意一点,且,
∴,③错误;
∵,
∴,
∵,,
∴,
∴,④正确;
即①②④正确;
故选:C.
7.A
解:A、根据图象知给自变量一个值,可能有2个函数值与其对应,故A选项不是函数,
B、根据图象知给自变量一个值,有且只有1个函数值与其对应,故B选项是函数,
C、根据图象知给自变量一个值,有且只有1个函数值与其对应,故C选项是函数,
D、根据图象知给自变量一个值,有且只有1个函数值与其对应,故D选项是函数,
故选:A.
8.A
解:根据题意,联立方程
解得
即点A的坐标为(-2,0)
又根据题意,可得点B(0,4),点C的坐标为(0,-2),点D的坐标为(-1,2)
中,BC=6,其高为点D的横坐标的长度,即为1,则
故答案为A.
9.D
解:根据路程=速度×时间得:汽车所走的路程s(千米)与所用的时间t(时)的关系表达式为:s=60t,故选D.
10.C
解:∵D是BC的中点,E是AC的中点,
∴△ADC的面积等于△ABC的面积的一半,△ADE的面积等于△ACD的面积的一半,
∴△ADE的面积等于△ABC的面积的四分之一,
又∵S△ADE=1,
∴S△ABC=4.
故答案为:4.
11.B
解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AEF+∠BFE=180°,
∵,
∴∠BFE=68°,
∴∠1=180°-2∠BFE=44°,
故选B.
12.B
解:作点P关于BD的对称点P′,作P′Q⊥CD交BD于K,交CD于Q,
∵AB=4,∠A=120°,
∴点P′到CD的距离为4×
=2,
∴PK+QK的最小值为2,
故选:B.
13.2
解:∵∠C=90°,DE⊥AB,
∴△AED和△ACD都是直角三角形,
在Rt△AED和Rt△ACD中,
DE=DC,AD=AD,
∴△AED≌△ACD(HL),
∴AE=AC=3,
∴BE=AB-AC=5-3=2.
故填:2.
14.(﹣5,﹣1)
解:根据题意,点Q的横坐标为:﹣2﹣3=﹣5;纵坐标为﹣3+2=﹣1;
即点Q的坐标是(﹣5,﹣1).
故答案为:(﹣5,﹣1).
15.7
解:∵这组数据的最大值是40,最小值是16,分组时取组距为4.
∴极差=40-16=24.
∵24÷4=6,
又∵数据不落在边界上,
∴这组数据的组数=6+1=7组.
故答案为:7
16.
解:(1)当点Q的坐标是(a,a)时,
a=-a+4,
解得a=2,
∴点Q的坐标是(2,2);
(2)当点Q的坐标是(b,-b)时,
-b=-b+4,
此方程无解.
∴点Q的坐标是(2,2).
故答案为:(2,2).
17.或
解:如下图:
∵点A(0、1)
∴OA=1
当直线与x轴相交于时,
∵直线与两坐标轴围成的三角形的面积为2,
∴,
解得,故(4、0)
设该直线的解析式为y=kx+1
将(4、0)代入得0=4k+1,解得
∴y=x+1
当直线与x轴相交于时,同理可求
将代入得0=-4k+1,解得
∴y=x+1
故该函数表达式为:y=x+1或y=x+1
故答案为
:y=x+1或y=x+1.
18.②
解:在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是中心对称图形,
这个正方形应该添加区域②处,
故答案为:②.
19.
解:∵AD是BC边上的高线,AD=6,AB=10,
∴∠D=90°,,
∵CE
是AB边上的中线,CD=AE,
∴,
取BD的中点F,连接CF,
∴EF为△ABD的中位线,
∴,EF//AD,
∴∠EFB=∠D=90°,
在Rt△BEF中,根据勾股定理,
,
∴DF=BD-BF=8-4=4,
∴CF=CD-DF=5-4=1,
在Rt△CEF中,根据勾股定理,
,
故答案为:.
20.
略
21.(1)见解析;(2);(3).
解:(1)如图,即为所求;
(2);
(3).
22.(1)16,40;(2)n=126,图见详解;(3)成绩优秀的学生有564名.
解:(1)由统计图及题意可得:抽取的总人数=24÷(20%-8%)=200(名),
∴(名),(名),
故答案为16,40;
(2)由图及(1)可得:
,
C组人数为:(人),
∴E组人数为:200-16-40-50-70=24(人),补全频数分布直方图如图所示:
(3)由(2)及题意可得:
(名);
答:成绩优秀的学生有564名.
23.(1)120°;(2)7
解:(1)平分,,,
,,
在Rt△AFD和Rt△AEB中,
,
∴Rt△AFD≌Rt△AEB(HL),
,
,
;
(2)∵Rt△AFD≌Rt△AEB,
,,
,
平分,
,
,,
,
在Rt△AFC和Rt△AEC中,
,
∴Rt△AFC≌Rt△AEC(HL),
,
四边形的面积.
24.(1)70°;(2)见解析.
(1)解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵CF平分∠DCB,
∴∠BCD=2∠BCF,
∵∠BCF=55°,
∴∠BCD=110°,
∴∠ABC=180°?110°=70°;
(2)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠BAD=∠DCB,
∴∠ABE=∠CDF,
∵AE,CF分别平分∠BAD和∠DCB,
∴∠BAE=∠BAD,∠DCF=∠DCB,
∴∠BAE=∠DCE,
∴△ABE≌△CDF(ASA),
∴BE=DF,
∴BE+EF=DF+EF,
即BF=DE.
25.(1)见解析;(2)见解析;(3)
(1)证明:∵四边形ABCD为矩形,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,
∴四边形ABEF是正方形;
(2)∵AE平分∠BAD,
∴∠DAG=∠BAE,
在△AGD和△ABE中,,
∴△AGD≌△ABE(AAS),
∴AB=AG;
(3)∵四边形ABEF是正方形,
∴AB=AF=1,
∵△AGD≌△ABE,
∴DG=AB=AF=AG=1,
∵AD=AE,
∴AD﹣AF=AE﹣AG,
即DF=EG,
在△DFO和△EGO中,,
∴△DFO≌△EGO(AAS),
∴FO=GO,FD=EG
∵∠DAE=∠AEF=45°,∠AFE=∠AGD=90°,
∴DF=FO=OG=EG,
∴DO=OF=OG,
∴DG=DO+OG=OG+OG=1,
∴OG==﹣1,
∴OD=(﹣1)=2﹣.
26.(1)直线AC的解析式为,AC边上的高为;(2);(3)存在,符合条件的t为1或1.5或6.5或.
解:(1)设直线AC的解析式为,将,代入得
,解得,
∴直线AC的解析式为,
∵,,,
∴,,,
∴,
设AC边上的高为h,
则,即,
解得,即AC边上的高为;
(2)当0≤t<2.5时,OP=5-2t,
∴△POA的面积,
当t>2.5时,OP=2t-5,
∴△POA的面积,
故;
(3)如图,当AP=AC时,
∵AO⊥BC,
∴PO=OC=3,BP=5-3=2,
∴此时t=1;
当PC=AC时,
∴BP=BC-PC=8-5=3或BP=BC+PC=8+5=13,
∴t=1.5或t=6.5;
当AP=PC时,
设PO=a,则CP=a+3,
∴,解得,
∴,
∴.
综上所述,存在,符合条件的t为1或1.5或6.5或.
27.(1)5;(2)7或;(3)
解:(1)根据题意知:,
∴,
∴的长为5;
(2)①当时,,,
∴;
②当时,过点作于点,
易得,.
在中,易得.
在中,,
∴,
解得:;
综上,当为7s或s时,为直角三角形;
(3)设.
∵在的垂直平分线上,
∴.
过点作于点.
易得.
在中,,
∴,
解得:,
∴的长为.
同课章节目录
