四年级数学下册课件 三角形的边 浙教版 42张ppt
文档属性
| 名称 | 四年级数学下册课件 三角形的边 浙教版 42张ppt |

|
|
| 格式 | zip | ||
| 文件大小 | 946.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-19 00:00:00 | ||
图片预览










文档简介
(共42张PPT)
三角形的边
一、回顾三角形的相关旧知
由三条线段围成的图形是三角形。
每相邻的两条线段端点相连。
什么样的图形是三角形?
二、试围三角形
是不是任意三根小棒都能围成一个三角形呢?
做实验!
小建议:
每位同学准备一些长短不同的小棒,从
中任取三根,围一围,看看结果怎样。
三、三角形的三边关系
3厘米
5厘米
6厘米
7厘米
9厘米
活动要求:
★从小棒中任选三根。
★记录每一根的长度。
★摆成图形贴在表中。
★说一说你有什么发现。
3厘米
5厘米
6厘米
7厘米
9厘米
小棒长度(厘米)
摆成的图形
第一根
第二根
第三根
小棒长度(厘米)
摆成的图形
第一根
第二根
第三根
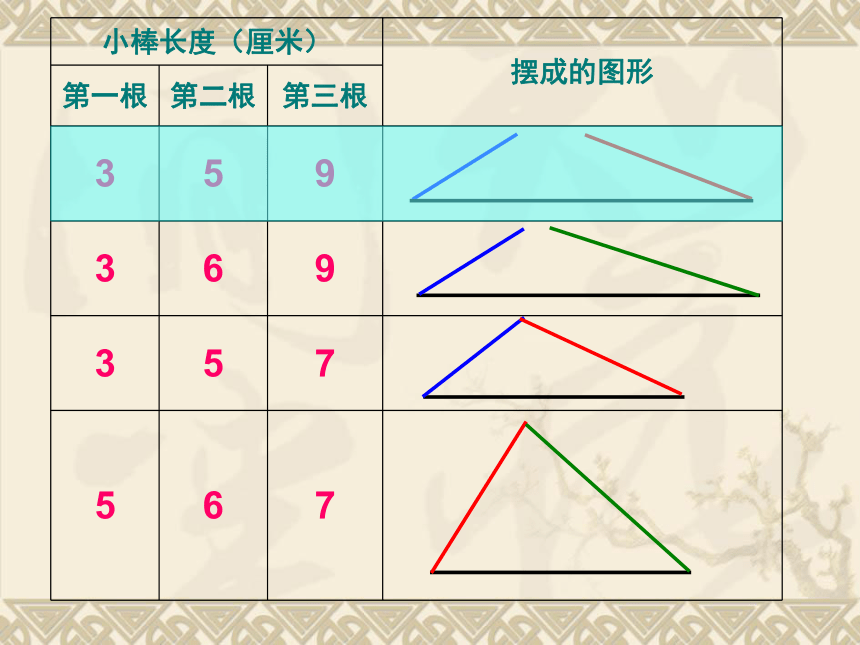
3
5
9
3
6
9
3
5
7
5
6
7
3厘米
5厘米
9厘米
3厘米
5厘米
9厘米
3厘米
5厘米
9厘米
3厘米
5厘米
9厘米
当较短的两根小棒的长度之和小于第三根小棒的时候,就围不成三角形。
3
+
5
<
9
小棒长度(厘米)
摆成的图形
第一根
第二根
第三根
3
5
9
3
6
9
3
5
7
5
6
7
9厘米
3厘米
6厘米
9厘米
3厘米
6厘米
9厘米
3厘米
6厘米
9厘米
3厘米
6厘米
当较短两根小棒的和等于第三根时也不能围成三角形。
3
+
6
=
9
小棒长度(厘米)
摆成的图形
第一根
第二根
第三根
3
5
9
3
6
9
3
5
7
5
6
7
什么情况下一定能围成三角形呢?
当较短的两根小棒的长度之和大于第三根小棒的时候,就可以围成三角形。
三条边长度(厘米)
三角形
第一条
第二条
第三条
3
5
7
5
6
7
3+5>7
5+6>7
3
5
7
5
6
7
三条边长度(厘米)
三角形
第一条
第二条
第三条
3
5
7
5
6
7
三角形的三边有什么关系?
三角形中任意两边之和都大于第三边。
3+5>7
3+7>5
5+7>3
5+6>7
5+7>6
6+7>5
3
5
7
5
6
7
用a、b、c三个字母表示三角形三条边的长度,那么,什么情况才能围成三角形?
a
+b>c
a+c>b
b+c>a
同时成立
三角形任意两边的和大于第三边。
四、判断能否围成三角形
在能围成三角形的一组线段后面打√,不能围成的打×。(用手势判断)
3cm
,8cm,
5cm
(
)
×
因为
3
+
5
=
8,
所以不能围成三角形。
在能围成三角形的一组线段后面打√,不能围成的打×。(用手势判断)
6cm
,4cm,
3cm
(
)
√
只要较短的两条线段的长度和大于第三条线段,就能围成三角形;否则,就不能围成三角形。
因为
6+4>3
6+3>4
4+3>6
所以能围成三角形。
6cm,
4cm,
3cm
6
6
6
在能围成三角形的各组小棒下面画“√”。(单位:厘米)
(
)
(
)
(
)
(
)
(5)1cm
2cm
3cm
(
)
(6)4cm
2cm
3cm
(
)
√
√
√
√
×
×
在能围成三角形的各组小棒下面画“√”。(单位:厘米)
(7)3cm
4cm
5cm
(
)
(8)3cm
3cm
3cm
(
)
√
√
√
×
(9)3cm
3cm
5cm
(
)
(10)2cm
6cm
2cm
(
)
五、解决上学路线问题
因为这三条路正好形成两个三角形,而中间的这条路相当于三角形的一条边,而在三角形中,其他两边之和一定大于第三边,所以中间的这条路最近。
六、开放练习
一根长3cm的小棒和一根长5cm的小棒,再配上一根几厘米的小棒就能围成一个三角形?
小棒长度(厘米)
能否围成三角形
第一根
第二根
第三根
3
5
3
5
3
5
3
5
3
5
3
5
3
5
3
5
列举法
√
×
√
√
√
×
2
3
4
5
6
7
8
1
×
√
有两根树干,一根长12米,另一根长8米,要做一个三角形。请你想一想,第三根树干可能有多长?
议一议:
第三根树干的长度
4
<
<
20
3厘米
4厘米
5厘米
8厘米
10厘米
五根小棒能摆出几组三角形?
想一想
七、解决实际问题
问题二
大
道
图
书
馆
教
学
楼
草坪
请勿
践踏!
尽管草地不允许踩,但还是被人们踩出了一条小路,这是为什么?我们能不能运用今天所学的知识解释这一现象?
明明家
学校
图书馆
明明上学
儿童乐园要建一个凉亭,亭子上部是三角形木架,现在已经准备了两根三米长的木料,假如你是设计师,第三根木料会准备多长(取整米数)
?并说明理由。
答:第三根木料可以是1米、2米、3米,4米、5米,因为第三根木料的长度应大于已知两根木料之差而小于两根木料之和。
两根木料之差为:3?3=0(米)
两根木料之和为:3+3=6(米)
说说你的收获
三角形的三边关系:
三角形任意两边的和大于第三边。
三角形的边
一、回顾三角形的相关旧知
由三条线段围成的图形是三角形。
每相邻的两条线段端点相连。
什么样的图形是三角形?
二、试围三角形
是不是任意三根小棒都能围成一个三角形呢?
做实验!
小建议:
每位同学准备一些长短不同的小棒,从
中任取三根,围一围,看看结果怎样。
三、三角形的三边关系
3厘米
5厘米
6厘米
7厘米
9厘米
活动要求:
★从小棒中任选三根。
★记录每一根的长度。
★摆成图形贴在表中。
★说一说你有什么发现。
3厘米
5厘米
6厘米
7厘米
9厘米
小棒长度(厘米)
摆成的图形
第一根
第二根
第三根
小棒长度(厘米)
摆成的图形
第一根
第二根
第三根
3
5
9
3
6
9
3
5
7
5
6
7
3厘米
5厘米
9厘米
3厘米
5厘米
9厘米
3厘米
5厘米
9厘米
3厘米
5厘米
9厘米
当较短的两根小棒的长度之和小于第三根小棒的时候,就围不成三角形。
3
+
5
<
9
小棒长度(厘米)
摆成的图形
第一根
第二根
第三根
3
5
9
3
6
9
3
5
7
5
6
7
9厘米
3厘米
6厘米
9厘米
3厘米
6厘米
9厘米
3厘米
6厘米
9厘米
3厘米
6厘米
当较短两根小棒的和等于第三根时也不能围成三角形。
3
+
6
=
9
小棒长度(厘米)
摆成的图形
第一根
第二根
第三根
3
5
9
3
6
9
3
5
7
5
6
7
什么情况下一定能围成三角形呢?
当较短的两根小棒的长度之和大于第三根小棒的时候,就可以围成三角形。
三条边长度(厘米)
三角形
第一条
第二条
第三条
3
5
7
5
6
7
3+5>7
5+6>7
3
5
7
5
6
7
三条边长度(厘米)
三角形
第一条
第二条
第三条
3
5
7
5
6
7
三角形的三边有什么关系?
三角形中任意两边之和都大于第三边。
3+5>7
3+7>5
5+7>3
5+6>7
5+7>6
6+7>5
3
5
7
5
6
7
用a、b、c三个字母表示三角形三条边的长度,那么,什么情况才能围成三角形?
a
+b>c
a+c>b
b+c>a
同时成立
三角形任意两边的和大于第三边。
四、判断能否围成三角形
在能围成三角形的一组线段后面打√,不能围成的打×。(用手势判断)
3cm
,8cm,
5cm
(
)
×
因为
3
+
5
=
8,
所以不能围成三角形。
在能围成三角形的一组线段后面打√,不能围成的打×。(用手势判断)
6cm
,4cm,
3cm
(
)
√
只要较短的两条线段的长度和大于第三条线段,就能围成三角形;否则,就不能围成三角形。
因为
6+4>3
6+3>4
4+3>6
所以能围成三角形。
6cm,
4cm,
3cm
6
6
6
在能围成三角形的各组小棒下面画“√”。(单位:厘米)
(
)
(
)
(
)
(
)
(5)1cm
2cm
3cm
(
)
(6)4cm
2cm
3cm
(
)
√
√
√
√
×
×
在能围成三角形的各组小棒下面画“√”。(单位:厘米)
(7)3cm
4cm
5cm
(
)
(8)3cm
3cm
3cm
(
)
√
√
√
×
(9)3cm
3cm
5cm
(
)
(10)2cm
6cm
2cm
(
)
五、解决上学路线问题
因为这三条路正好形成两个三角形,而中间的这条路相当于三角形的一条边,而在三角形中,其他两边之和一定大于第三边,所以中间的这条路最近。
六、开放练习
一根长3cm的小棒和一根长5cm的小棒,再配上一根几厘米的小棒就能围成一个三角形?
小棒长度(厘米)
能否围成三角形
第一根
第二根
第三根
3
5
3
5
3
5
3
5
3
5
3
5
3
5
3
5
列举法
√
×
√
√
√
×
2
3
4
5
6
7
8
1
×
√
有两根树干,一根长12米,另一根长8米,要做一个三角形。请你想一想,第三根树干可能有多长?
议一议:
第三根树干的长度
4
<
<
20
3厘米
4厘米
5厘米
8厘米
10厘米
五根小棒能摆出几组三角形?
想一想
七、解决实际问题
问题二
大
道
图
书
馆
教
学
楼
草坪
请勿
践踏!
尽管草地不允许踩,但还是被人们踩出了一条小路,这是为什么?我们能不能运用今天所学的知识解释这一现象?
明明家
学校
图书馆
明明上学
儿童乐园要建一个凉亭,亭子上部是三角形木架,现在已经准备了两根三米长的木料,假如你是设计师,第三根木料会准备多长(取整米数)
?并说明理由。
答:第三根木料可以是1米、2米、3米,4米、5米,因为第三根木料的长度应大于已知两根木料之差而小于两根木料之和。
两根木料之差为:3?3=0(米)
两根木料之和为:3+3=6(米)
说说你的收获
三角形的三边关系:
三角形任意两边的和大于第三边。
同课章节目录
- 一 自然数与整数
- 1.自然数
- 2.认识负数
- 3.整除
- 4.能被2,5整除的数
- 5.能被3整除的数
- 6.倍数与因数
- 7.素数与合数
- 8.分解因数
- 二 可能性
- 9.认识可能性
- 三 分数与除法
- 10.分数与除法的关系
- 11.一个数是另一个数的几分之几
- 12.真分数与假分数
- 13.假分数与整数
- 14.假分数与带分数
- 四 几何小天地
- 15.角的度量
- 16.角的分类
- 17.轴对称图形
- 18.图形的旋转
- 19.三角形的边
- 20.三角形的角
- 21.三角形内角和
- 22.平行四边形的边与角
- 23.梯形的边与角
- 24.图形的高与底
- 五 代数式与方程
- 25.代数式(一)
- 26.代数式(二)
- 27.认识方程
- 28.等式的性质
- 29.解方程
- 30.列方程解题(一)
- 31.列方程解题(二)
- 六 总复习
