周滚动练 24.2 点和圆、直线与圆的位置关系 2021---2022学年九年级数学人教版上册(Word版含答案)
文档属性
| 名称 | 周滚动练 24.2 点和圆、直线与圆的位置关系 2021---2022学年九年级数学人教版上册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 142.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-20 11:15:38 | ||
图片预览


文档简介
周滚动练(24.2)
(时间:40分钟 满分:100分)
一、选择题(每小题4分,共28分)
1.用反证法证明“在△ABC中,如果∠B≠∠C,那么AB≠AC
“时,应假设
( )
A.AB=AC
B.∠B=∠C
C.AB≠AC
D.∠B≠∠C
2.已知过☉O内一点M的最长弦长为12
cm,最短弦长为8
cm,那么OM的长度为
( )
A.6
cm
B.9
cm
C.4
cm
D.2
cm
3.如图,在矩形ABCD中,AB=6,AD=8.若以点A为圆心,以8为半径作圆,则下列各点在☉A外的是
( )
A.点A
B.点B
C.点C
D.点D
4.在Rt△ABC中,∠C=90°,AC=8
cm,AB=10
cm,以点C为圆心,以9
cm长为直径的☉C与直线AB的位置关系为( )
A.相交
B.相离
C.相切
D.相离或相交
5.如图,点A,B,C分别表示三个村庄,AB=13千米,BC=5千米,AC=12千米.某社区拟建一个文化活动中心.要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在
( )
A.AB的中点
B.BC的中点
C.AC的中点
D.∠C的平分线与AB的交点
6.如图,☉O1的半径为1,正方形ABCD的边长为4,点O2为正方形ABCD的中心,O1O2⊥CD于点P,O1O2=5.现将☉O1绕点P按顺时针方向旋转180°,则在旋转过程中,☉O1与正方形ABCD的边只有一个公共点的情况一共出现
( )
A.1次
B.2次
C.3次
D.4次
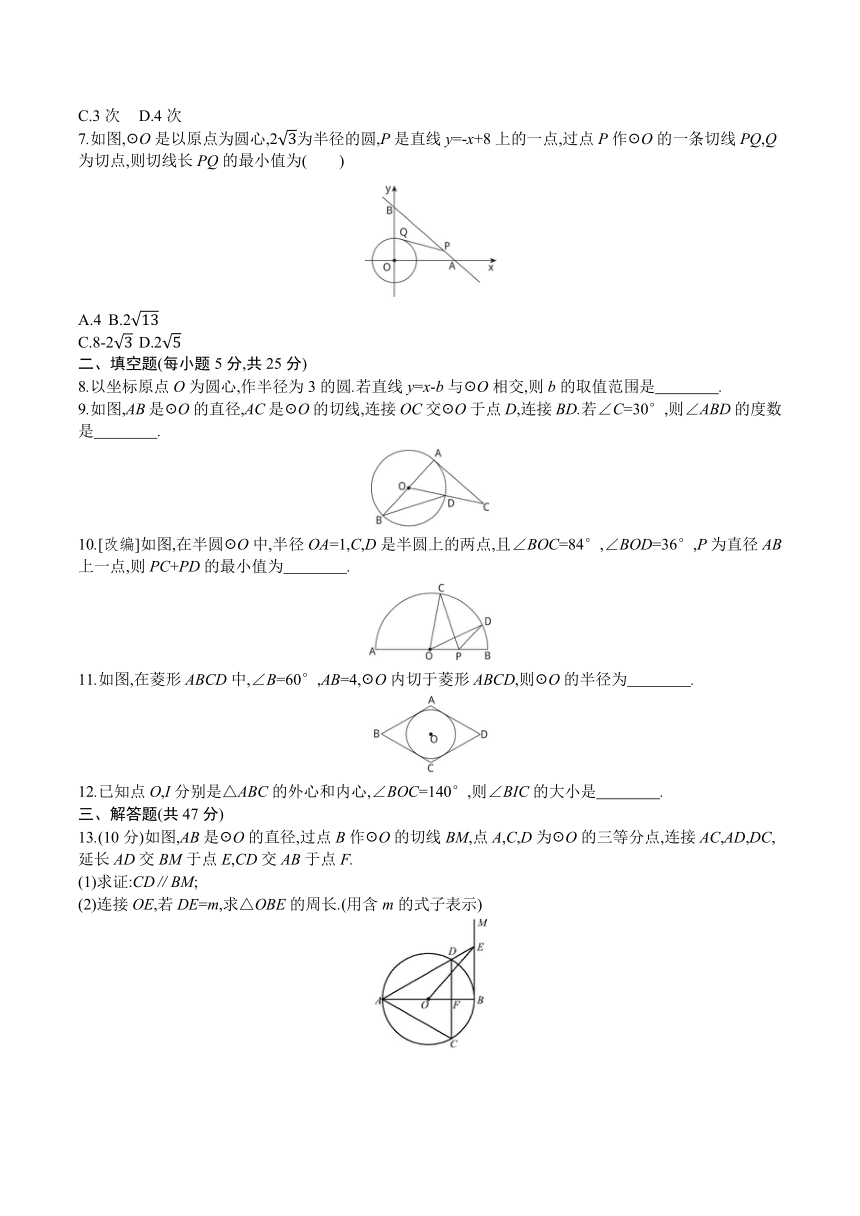
7.如图,☉O是以原点为圆心,2为半径的圆,P是直线y=-x+8上的一点,过点P作☉O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
A.4
B.2
C.8-2
D.2
二、填空题(每小题5分,共25分)
8.以坐标原点O为圆心,作半径为3的圆.若直线y=x-b与☉O相交,则b的取值范围是 .?
9.如图,AB是☉O的直径,AC是☉O的切线,连接OC交☉O于点D,连接BD.若∠C=30°,则∠ABD的度数是 .?
10.[改编]如图,在半圆☉O中,半径OA=1,C,D是半圆上的两点,且∠BOC=84°,∠BOD=36°,P为直径AB上一点,则PC+PD的最小值为 .?
11.如图,在菱形ABCD中,∠B=60°,AB=4,☉O内切于菱形ABCD,则☉O的半径为 .?
12.已知点O,I分别是△ABC的外心和内心,∠BOC=140°,则∠BIC的大小是 .?
三、解答题(共47分)
13.(10分)如图,AB是☉O的直径,过点B作☉O的切线BM,点A,C,D为☉O的三等分点,连接AC,AD,DC,延长AD交BM于点E,CD交AB于点F.
(1)求证:CD∥BM;
(2)连接OE,若DE=m,求△OBE的周长.(用含m的式子表示)
14.(12分)如图,在△ABC中,A,B,C三点的坐标分别为A(0,8),B(-6,0),C(15,0).若△ABC的内心为D,求点D的坐标.
15.(12分)如图,以四边形ABCD的对角线BD为直径作圆,圆心为O,过点A作AE⊥CD交CD的延长线于点E,且DA平分∠BDE.
(1)求证:AE是☉O的切线;
(2)若AE=4,CD=6,求☉O的半径和AD的长.
16.(13分)如图,等腰直角△ABC的顶点A在☉O上,直角边AC和斜边AB分别交☉O于D,E两点,连接DE,OD.
(1)求∠ODE的度数;
(2)若D是AC的中点,∠ODA=60°,BC=4,求BE的长.
周滚动练(24.2)
1.A 2.D 3.C 4.B 5.A 6.C 7.D 8.-313.解:(1)∵A,C,D为☉O的三等分点,
∴,∴AD=DC=AC,∴△ACD为等边三角形.
又∵点O为△ACD的外心,∴AB⊥CD.
∵BM为☉O的切线,∴BE⊥AB,∴CD∥BM.
(2)连接BD.由(1)知△ACD为等边三角形,∴∠C=60°,
∴∠ABD=∠C=60°,∴∠DBE=30°.
在Rt△BDE中,BE=2DE=2m,BD=DE=m.
在Rt△ABD中,AB=2BD=2m,∴OB=m.
在Rt△OBE中,OE=m,
∴△OBE的周长为2m+m+m=(2+)m.
14.解:如图,连接DA,DB,DC,DM,DN,DP.
∵☉D为△ABC的内切圆,∴AN=AP(设为λ),BM=BN(设为μ),CM=CP(设为γ),DM⊥BC,DN⊥AB,DP⊥AC.
∵A,B,C三点的坐标分别为A(0,8),B(-6,0),C(15,0),
∴AB=10,AC=17,BC=21,
∴解得γ=14,即CM=14,
∴OM=OC-CM=15-14=1.
设☉D的半径为φ,∴由面积公式得BC·AO=(AB+AC+BC)·φ,解得φ=,即DM=.
综上所述,点D的坐标为.
15.解:(1)连接OA.∵AE⊥CD,∴∠DAE+∠ADE=90°.
∵DA平分∠BDE,∴∠ADE=∠ADO.
又∵OA=OD,∴∠OAD=∠ADO,∴∠DAE+∠OAD=90°,
∴OA⊥AE,∴AE是☉O的切线.
(2)取CD的中点F,连接OF.
由题可知四边形AEFO是矩形.
∵CD=6,∴DF=FC=3.
在Rt△OFD中,OF=AE=4,∴OD==5,
∴EF=OA=OD=5.
在Rt△AED中,AE=4,ED=EF-DF=2,
∴AD==2.
综上所述,☉O的半径为5,AD的长为2.
16.解:(1)连接OE.∵∠BAC=45°,∴∠DOE=90°.
∵OD=OE,∴∠ODE=45°.
(2)过点D作DF⊥AB于点F,连接OA.
∵∠ODA=60°,OA=OD,∴△OAD是等边三角形,
∴∠AOD=60°,∴∠AED=30°.
在Rt△ADF中,∠DAF=45°,AD=AC=BC=2,
∴AF=DF=AD=.
在Rt△DEF中,DE=2DF=2,∴EF=,∴AE=AF+EF=.
∵△ABC是等腰直角三角形,BC=4,∴AB=BC=4,
∴BE=AB-AE=4-()=3.
(时间:40分钟 满分:100分)
一、选择题(每小题4分,共28分)
1.用反证法证明“在△ABC中,如果∠B≠∠C,那么AB≠AC
“时,应假设
( )
A.AB=AC
B.∠B=∠C
C.AB≠AC
D.∠B≠∠C
2.已知过☉O内一点M的最长弦长为12
cm,最短弦长为8
cm,那么OM的长度为
( )
A.6
cm
B.9
cm
C.4
cm
D.2
cm
3.如图,在矩形ABCD中,AB=6,AD=8.若以点A为圆心,以8为半径作圆,则下列各点在☉A外的是
( )
A.点A
B.点B
C.点C
D.点D
4.在Rt△ABC中,∠C=90°,AC=8
cm,AB=10
cm,以点C为圆心,以9
cm长为直径的☉C与直线AB的位置关系为( )
A.相交
B.相离
C.相切
D.相离或相交
5.如图,点A,B,C分别表示三个村庄,AB=13千米,BC=5千米,AC=12千米.某社区拟建一个文化活动中心.要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在
( )
A.AB的中点
B.BC的中点
C.AC的中点
D.∠C的平分线与AB的交点
6.如图,☉O1的半径为1,正方形ABCD的边长为4,点O2为正方形ABCD的中心,O1O2⊥CD于点P,O1O2=5.现将☉O1绕点P按顺时针方向旋转180°,则在旋转过程中,☉O1与正方形ABCD的边只有一个公共点的情况一共出现
( )
A.1次
B.2次
C.3次
D.4次
7.如图,☉O是以原点为圆心,2为半径的圆,P是直线y=-x+8上的一点,过点P作☉O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
A.4
B.2
C.8-2
D.2
二、填空题(每小题5分,共25分)
8.以坐标原点O为圆心,作半径为3的圆.若直线y=x-b与☉O相交,则b的取值范围是 .?
9.如图,AB是☉O的直径,AC是☉O的切线,连接OC交☉O于点D,连接BD.若∠C=30°,则∠ABD的度数是 .?
10.[改编]如图,在半圆☉O中,半径OA=1,C,D是半圆上的两点,且∠BOC=84°,∠BOD=36°,P为直径AB上一点,则PC+PD的最小值为 .?
11.如图,在菱形ABCD中,∠B=60°,AB=4,☉O内切于菱形ABCD,则☉O的半径为 .?
12.已知点O,I分别是△ABC的外心和内心,∠BOC=140°,则∠BIC的大小是 .?
三、解答题(共47分)
13.(10分)如图,AB是☉O的直径,过点B作☉O的切线BM,点A,C,D为☉O的三等分点,连接AC,AD,DC,延长AD交BM于点E,CD交AB于点F.
(1)求证:CD∥BM;
(2)连接OE,若DE=m,求△OBE的周长.(用含m的式子表示)
14.(12分)如图,在△ABC中,A,B,C三点的坐标分别为A(0,8),B(-6,0),C(15,0).若△ABC的内心为D,求点D的坐标.
15.(12分)如图,以四边形ABCD的对角线BD为直径作圆,圆心为O,过点A作AE⊥CD交CD的延长线于点E,且DA平分∠BDE.
(1)求证:AE是☉O的切线;
(2)若AE=4,CD=6,求☉O的半径和AD的长.
16.(13分)如图,等腰直角△ABC的顶点A在☉O上,直角边AC和斜边AB分别交☉O于D,E两点,连接DE,OD.
(1)求∠ODE的度数;
(2)若D是AC的中点,∠ODA=60°,BC=4,求BE的长.
周滚动练(24.2)
1.A 2.D 3.C 4.B 5.A 6.C 7.D 8.-3
∴,∴AD=DC=AC,∴△ACD为等边三角形.
又∵点O为△ACD的外心,∴AB⊥CD.
∵BM为☉O的切线,∴BE⊥AB,∴CD∥BM.
(2)连接BD.由(1)知△ACD为等边三角形,∴∠C=60°,
∴∠ABD=∠C=60°,∴∠DBE=30°.
在Rt△BDE中,BE=2DE=2m,BD=DE=m.
在Rt△ABD中,AB=2BD=2m,∴OB=m.
在Rt△OBE中,OE=m,
∴△OBE的周长为2m+m+m=(2+)m.
14.解:如图,连接DA,DB,DC,DM,DN,DP.
∵☉D为△ABC的内切圆,∴AN=AP(设为λ),BM=BN(设为μ),CM=CP(设为γ),DM⊥BC,DN⊥AB,DP⊥AC.
∵A,B,C三点的坐标分别为A(0,8),B(-6,0),C(15,0),
∴AB=10,AC=17,BC=21,
∴解得γ=14,即CM=14,
∴OM=OC-CM=15-14=1.
设☉D的半径为φ,∴由面积公式得BC·AO=(AB+AC+BC)·φ,解得φ=,即DM=.
综上所述,点D的坐标为.
15.解:(1)连接OA.∵AE⊥CD,∴∠DAE+∠ADE=90°.
∵DA平分∠BDE,∴∠ADE=∠ADO.
又∵OA=OD,∴∠OAD=∠ADO,∴∠DAE+∠OAD=90°,
∴OA⊥AE,∴AE是☉O的切线.
(2)取CD的中点F,连接OF.
由题可知四边形AEFO是矩形.
∵CD=6,∴DF=FC=3.
在Rt△OFD中,OF=AE=4,∴OD==5,
∴EF=OA=OD=5.
在Rt△AED中,AE=4,ED=EF-DF=2,
∴AD==2.
综上所述,☉O的半径为5,AD的长为2.
16.解:(1)连接OE.∵∠BAC=45°,∴∠DOE=90°.
∵OD=OE,∴∠ODE=45°.
(2)过点D作DF⊥AB于点F,连接OA.
∵∠ODA=60°,OA=OD,∴△OAD是等边三角形,
∴∠AOD=60°,∴∠AED=30°.
在Rt△ADF中,∠DAF=45°,AD=AC=BC=2,
∴AF=DF=AD=.
在Rt△DEF中,DE=2DF=2,∴EF=,∴AE=AF+EF=.
∵△ABC是等腰直角三角形,BC=4,∴AB=BC=4,
∴BE=AB-AE=4-()=3.
同课章节目录
