小学数学西师大版六年级下 总复习 图形与几何(2) 课件(59页PPT)
文档属性
| 名称 | 小学数学西师大版六年级下 总复习 图形与几何(2) 课件(59页PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-21 00:00:00 | ||
图片预览


文档简介
立 体 图 形
第 五 单元 总复习
图形与几何
学习目标
复习小学阶段所学的立体图形的特征以及表面积和体积的计算方法,将其按类进行概括,形成知识体系。
在具体操作、讨论等活动中,进一步整理学过的有关立体图形方面的知识,并掌握相应的技能。
在系统复习的过程中,体验与同学合作交流以及获取知识的乐趣,增进对数学学习的积极情感,增强学好数学的信心。
情境导入
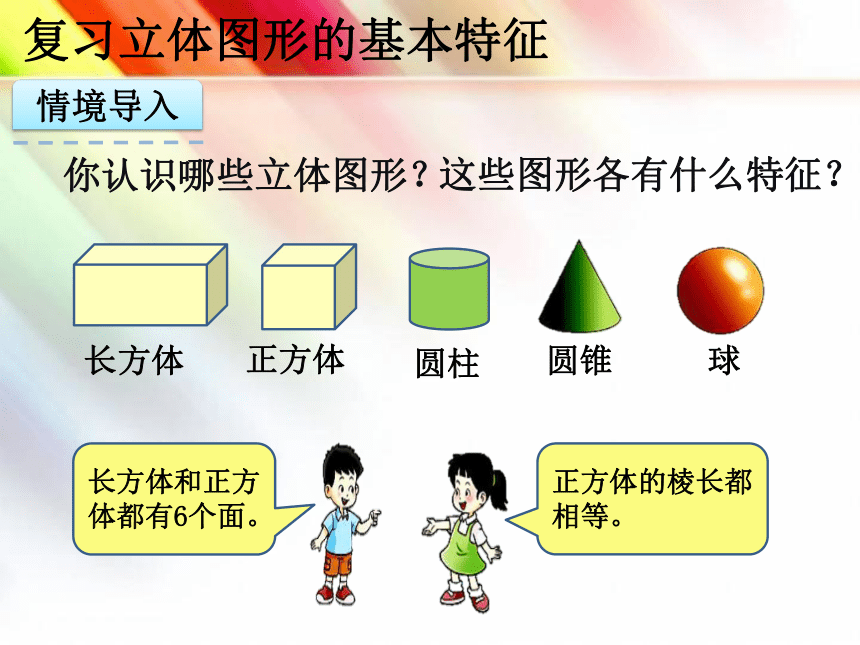
你认识哪些立体图形?
长方体和正方体都有6个面。
正方体的棱长都相等。
长方体
正方体
圆柱
圆锥
球
复习立体图形的基本特征
这些图形各有什么特征?
形
体
面
棱
顶点
面的形状
面积
棱长
长
方
体
正
方
体
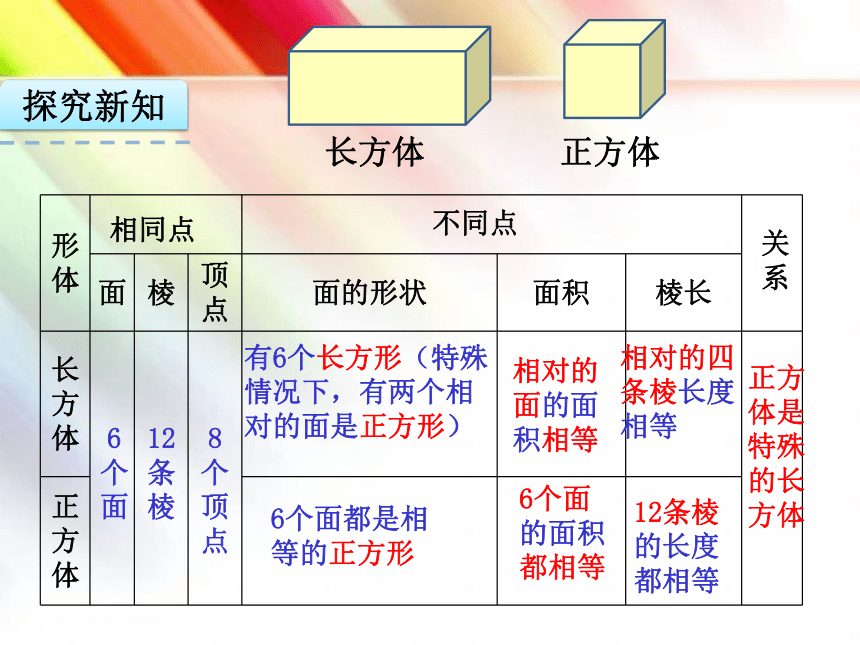
探究新知
长方体
有6个长方形(特殊情况下,有两个相对的面是正方形)
6个面都是相等的正方形
相对的面的面积相等
6个面的面积都相等
12条棱的长度都相等
相对的四条棱长度相等
正方体是特殊的长方体
正方体
6个面
12条棱
8个顶点
相同点
不同点
关系
探究新知
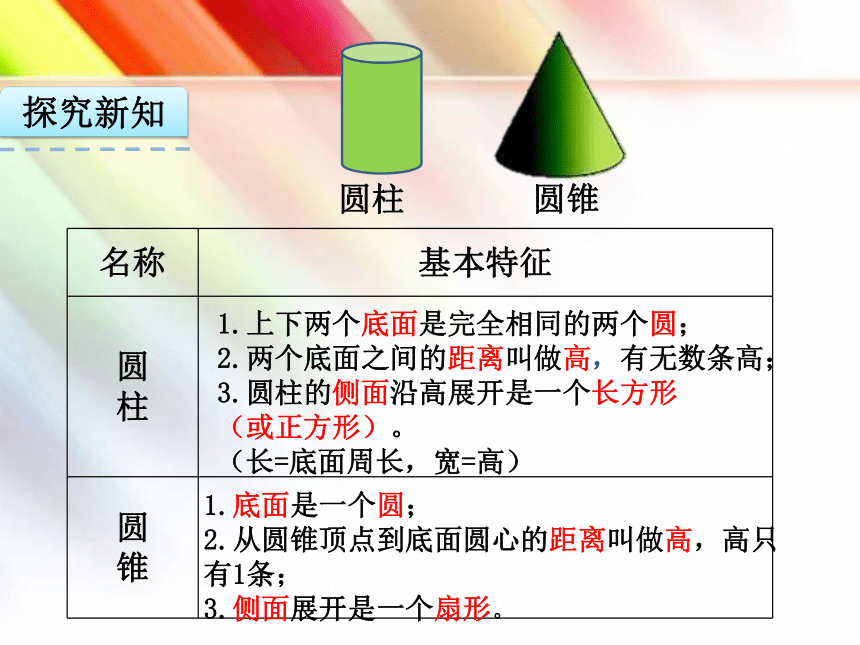
圆柱
圆锥
名称
基本特征
圆
柱
圆
锥
1.上下两个底面是完全相同的两个圆;
2.两个底面之间的距离叫做高,有无数条高;
3.圆柱的侧面沿高展开是一个长方形
(或正方形)。
(长=底面周长,宽=高)
1.底面是一个圆;
2.从圆锥顶点到底面圆心的距离叫做高,高只有1条;
3.侧面展开是一个扇形。
探究新知
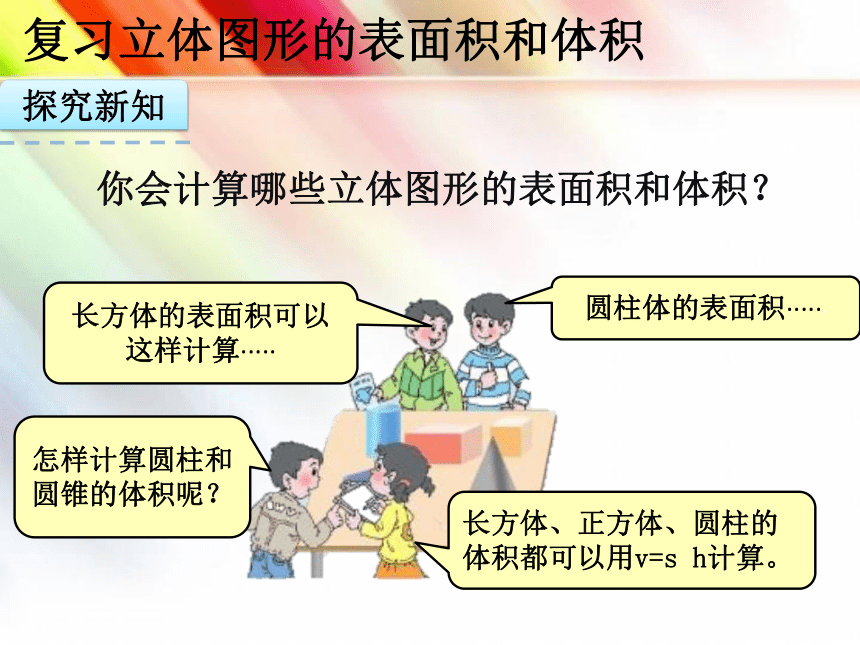
你会计算哪些立体图形的表面积和体积?
长方体的表面积可以这样计算·····
怎样计算圆柱和圆锥的体积呢?
圆柱体的表面积······
长方体、正方体、圆柱的体积都可以用v=s h计算。
复习立体图形的表面积和体积
探究新知
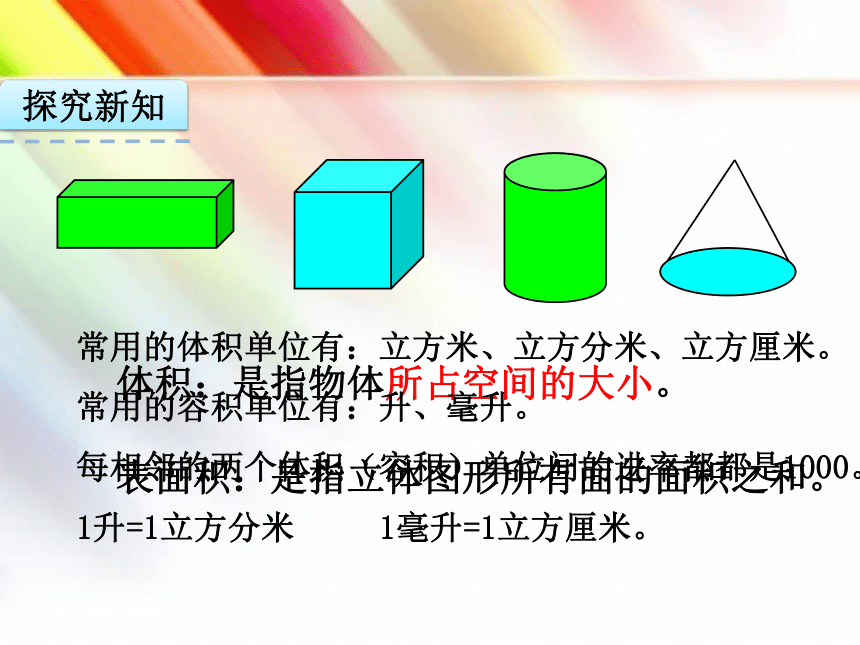
体积:是指物体所占空间的大小。
表面积:是指立体图形所有面的面积之和。
常用的体积单位有:立方米、立方分米、立方厘米。
常用的容积单位有:升、毫升。
每相邻的两个体积(容积)单位间的进率都都是1000。
1升=1立方分米 1毫升=1立方厘米。
探究新知
a
b
h
a
a
a
h
r
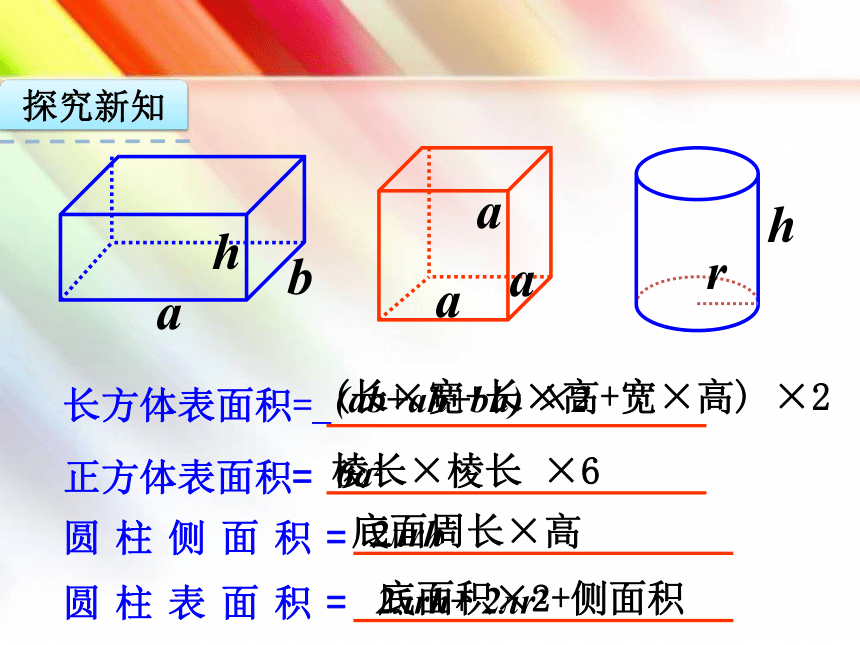
长方体表面积=
正方体表面积=
圆柱侧面积=
圆柱表面积=
(ab+ah+bh) ×2
6a
2лrh
2лrh+ 2лr
2
2
(长×宽+长×高+宽×高) ×2
棱长×棱长 ×6
底面周长×高
底面积×2+侧面积
h
a
b
a
a
a
s
h
s
h
探究新知
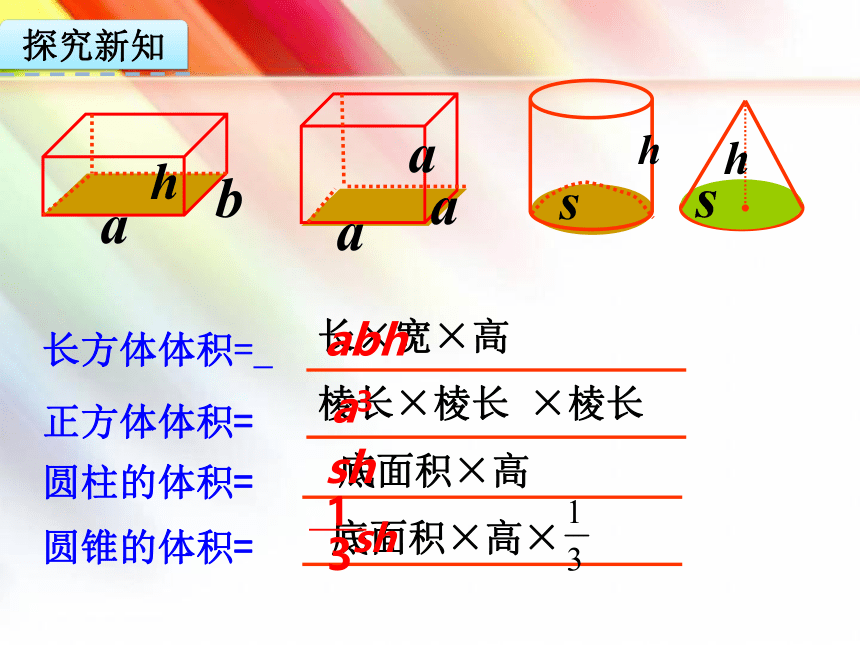
长方体体积=
正方体体积=
圆柱的体积=
圆锥的体积=
长×宽×高
棱长×棱长 ×棱长
底面积×高
底面积×高×
abh
a3
sh
sh
1
3
V=
V=
V=
V=
abh
a3
sh
1
3
sh
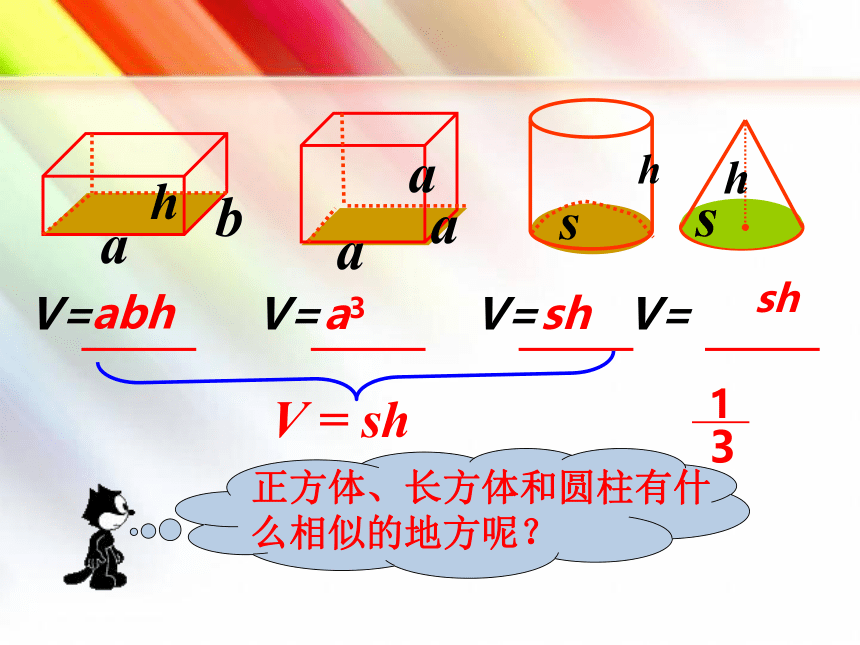
V = sh
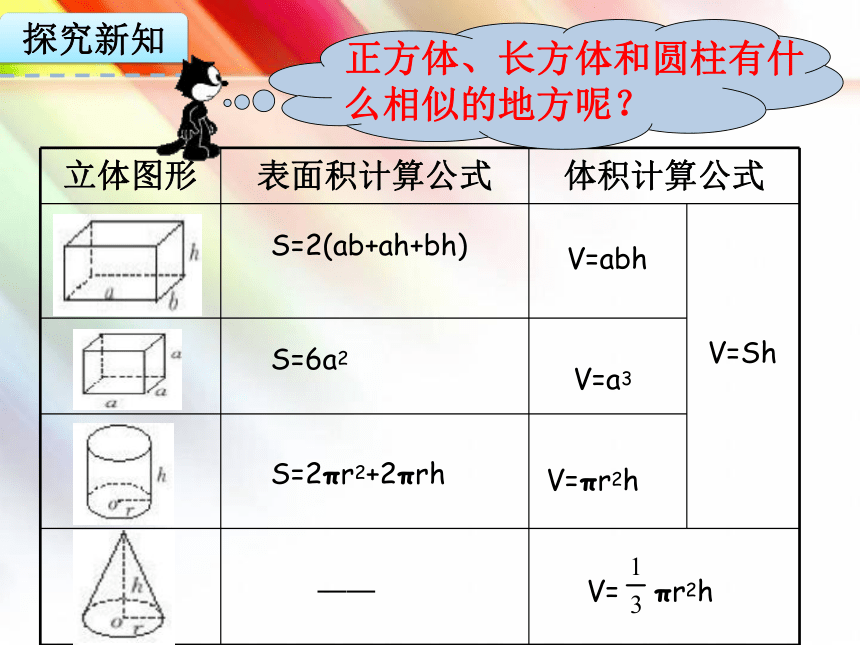
正方体、长方体和圆柱有什么相似的地方呢?
h
a
b
a
a
a
s
h
s
h
探究新知
立体图形
表面积计算公式
体积计算公式
S=2(ab+ah+bh)
S=6a2
S=2πr2+2πrh
——
V=abh
V=a3
V=πr2h
V= πr2h
V=Sh
正方体、长方体和圆柱有什么相似的地方呢?
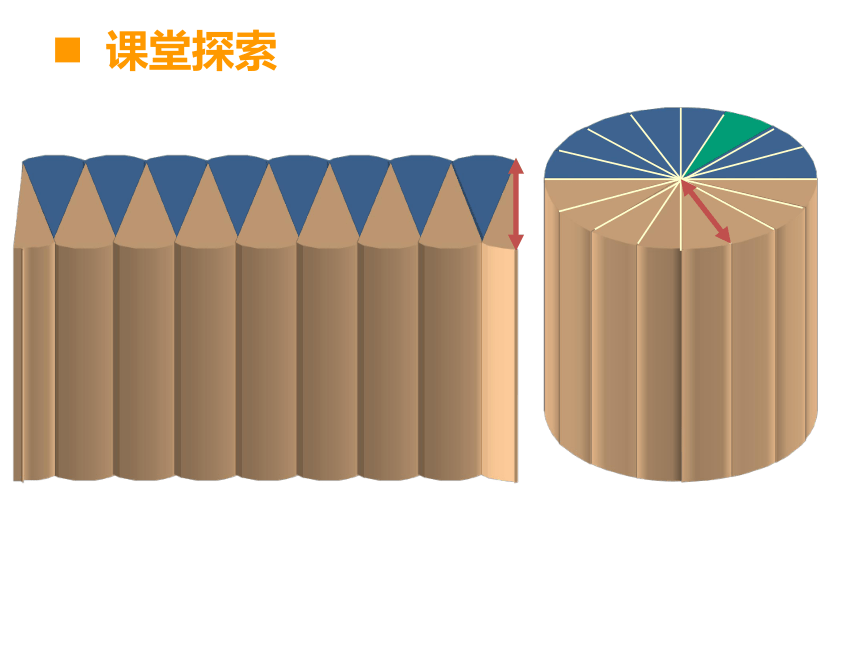
课堂探索
长方体的体积=底面积×高
底面积
课堂探索
底面积
长方体的体积=底面积×高
课堂探索
底面积
长方体的体积=底面积×高
课堂探索
高
长方体的体积=底面积×高
圆柱体的体积=
×
底面积
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
探究新知
找一找
立体图形的表面积和体积有什么区别?
1. 表示的意义不同;
2. 计量单位不同;
3. 计算方法不同。
探究新知
时代广场有一个圆柱形水池,底面直径5m,深0.8m。
探究新知
时代广场有一个圆柱形水池,底面直径5m,深0.8m。
(1)如果要在水池的底部和内壁贴上瓷砖,贴瓷砖的面积是多少平方米?
3.14×(5÷2)2+3.14 ×5 ×0.8
=19.625+12.56
=32.185(m2)
答:贴瓷砖的面积是32.185m2。
解决这个问题要用到哪些知识?请独立解决后再交流。
探究新知
时代广场有一个圆柱形水池,底面直径5m,深0.8m。
(2)每平方米瓷砖25.5元,购买瓷砖需要多少元?
25.5×32.185
820.72(元)
≈
答:购买瓷砖约需要820.72元。
探究新知
时代广场有一个圆柱形水池,底面直径5m,深0.8m。
(3)每立方米水重1吨,这个水池最多能装多少吨水?
3.14×(5÷2)2×0.8×1
=3.14×5
答:这个水池最多能装15.7吨水。
=15.7(吨)
表面积:
体积:
2(aa+ah+ah)
aah
a
a
h
课堂活动
1cm
2cm
表面积:
3.14×12×2+3.14 ×1 ×1×2
=12.56(平方厘米)
体积:
3.14×12×2
=6.28(立方厘米)
课堂活动
课堂 总结
通过这节课的学习,你学会了什么?
我会计算立体图形的表面积和体积。
我知道立体图形的体积计算公式是怎样得到的。
第 五 单元 总复习
图形与几何
学习目标
复习小学阶段所学的立体图形的特征以及表面积和体积的计算方法,将其按类进行概括,形成知识体系。
在具体操作、讨论等活动中,进一步整理学过的有关立体图形方面的知识,并掌握相应的技能。
在系统复习的过程中,体验与同学合作交流以及获取知识的乐趣,增进对数学学习的积极情感,增强学好数学的信心。
情境导入
你认识哪些立体图形?
长方体和正方体都有6个面。
正方体的棱长都相等。
长方体
正方体
圆柱
圆锥
球
复习立体图形的基本特征
这些图形各有什么特征?
形
体
面
棱
顶点
面的形状
面积
棱长
长
方
体
正
方
体
探究新知
长方体
有6个长方形(特殊情况下,有两个相对的面是正方形)
6个面都是相等的正方形
相对的面的面积相等
6个面的面积都相等
12条棱的长度都相等
相对的四条棱长度相等
正方体是特殊的长方体
正方体
6个面
12条棱
8个顶点
相同点
不同点
关系
探究新知
圆柱
圆锥
名称
基本特征
圆
柱
圆
锥
1.上下两个底面是完全相同的两个圆;
2.两个底面之间的距离叫做高,有无数条高;
3.圆柱的侧面沿高展开是一个长方形
(或正方形)。
(长=底面周长,宽=高)
1.底面是一个圆;
2.从圆锥顶点到底面圆心的距离叫做高,高只有1条;
3.侧面展开是一个扇形。
探究新知
你会计算哪些立体图形的表面积和体积?
长方体的表面积可以这样计算·····
怎样计算圆柱和圆锥的体积呢?
圆柱体的表面积······
长方体、正方体、圆柱的体积都可以用v=s h计算。
复习立体图形的表面积和体积
探究新知
体积:是指物体所占空间的大小。
表面积:是指立体图形所有面的面积之和。
常用的体积单位有:立方米、立方分米、立方厘米。
常用的容积单位有:升、毫升。
每相邻的两个体积(容积)单位间的进率都都是1000。
1升=1立方分米 1毫升=1立方厘米。
探究新知
a
b
h
a
a
a
h
r
长方体表面积=
正方体表面积=
圆柱侧面积=
圆柱表面积=
(ab+ah+bh) ×2
6a
2лrh
2лrh+ 2лr
2
2
(长×宽+长×高+宽×高) ×2
棱长×棱长 ×6
底面周长×高
底面积×2+侧面积
h
a
b
a
a
a
s
h
s
h
探究新知
长方体体积=
正方体体积=
圆柱的体积=
圆锥的体积=
长×宽×高
棱长×棱长 ×棱长
底面积×高
底面积×高×
abh
a3
sh
sh
1
3
V=
V=
V=
V=
abh
a3
sh
1
3
sh
V = sh
正方体、长方体和圆柱有什么相似的地方呢?
h
a
b
a
a
a
s
h
s
h
探究新知
立体图形
表面积计算公式
体积计算公式
S=2(ab+ah+bh)
S=6a2
S=2πr2+2πrh
——
V=abh
V=a3
V=πr2h
V= πr2h
V=Sh
正方体、长方体和圆柱有什么相似的地方呢?
课堂探索
长方体的体积=底面积×高
底面积
课堂探索
底面积
长方体的体积=底面积×高
课堂探索
底面积
长方体的体积=底面积×高
课堂探索
高
长方体的体积=底面积×高
圆柱体的体积=
×
底面积
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
探究新知
找一找
立体图形的表面积和体积有什么区别?
1. 表示的意义不同;
2. 计量单位不同;
3. 计算方法不同。
探究新知
时代广场有一个圆柱形水池,底面直径5m,深0.8m。
探究新知
时代广场有一个圆柱形水池,底面直径5m,深0.8m。
(1)如果要在水池的底部和内壁贴上瓷砖,贴瓷砖的面积是多少平方米?
3.14×(5÷2)2+3.14 ×5 ×0.8
=19.625+12.56
=32.185(m2)
答:贴瓷砖的面积是32.185m2。
解决这个问题要用到哪些知识?请独立解决后再交流。
探究新知
时代广场有一个圆柱形水池,底面直径5m,深0.8m。
(2)每平方米瓷砖25.5元,购买瓷砖需要多少元?
25.5×32.185
820.72(元)
≈
答:购买瓷砖约需要820.72元。
探究新知
时代广场有一个圆柱形水池,底面直径5m,深0.8m。
(3)每立方米水重1吨,这个水池最多能装多少吨水?
3.14×(5÷2)2×0.8×1
=3.14×5
答:这个水池最多能装15.7吨水。
=15.7(吨)
表面积:
体积:
2(aa+ah+ah)
aah
a
a
h
课堂活动
1cm
2cm
表面积:
3.14×12×2+3.14 ×1 ×1×2
=12.56(平方厘米)
体积:
3.14×12×2
=6.28(立方厘米)
课堂活动
课堂 总结
通过这节课的学习,你学会了什么?
我会计算立体图形的表面积和体积。
我知道立体图形的体积计算公式是怎样得到的。
