2021-2022学年度人教版七年级数学上册暑假预习练习(Word版含解答):1.4 有理数的乘除法
文档属性
| 名称 | 2021-2022学年度人教版七年级数学上册暑假预习练习(Word版含解答):1.4 有理数的乘除法 |  | |
| 格式 | docx | ||
| 文件大小 | 76.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-20 13:50:18 | ||
图片预览




文档简介
2021-2022学年度人教版七年级数学上册暑假预习练习(Word版含解答):1.4 有理数的乘除法
一、选择题
1.计算: (-8)÷2 的结果是(?? )
A.?3?????????????????????B.?4???????????????????????C.?6?????????????????????????D.?16
2.计算(﹣3)×(﹣1)的结果是( )
A.?﹣4?????????????????????B.?﹣3????????????????????????????C.?3??????????????????????????D.?4
3.在-4,-2,0,1,3,5这六个数中,任意三数之积的最大值是(?? )
A.?15??????????????????B.?40???????????????????C.?24???????????????????D.?30
4.(阅读理解)计算: 25×11=275 , 13×11=143 , 48×11=528 , 74×11=814 ,观察算式,我们发现两位数乘11的速算方法:头尾一拉,中间相加,满十进一.
(拓展应用)已知一个两位数,十位上的数字是 a ,个位上的数字是 b ,这个两位数乘11,计算结果中十位上的数字可表示为(?? )
A.?a 或 a+1????????B.?a+b 或 ab??????????????C.?a+b-10????????????D.?a+b 或 a+b-10
5.m 的相反数是 -6 , n 倒数是 13 ,则 mn 的值是(?? )
A.?-18????????????????????B.?18???????????????????????C.?2????????????????????????????D.?-2
6.早在两千多年前,中国人已经开始使用负数,并应用到生产和生活中.中国人使用负数在世界上是首创.下列各式计算结果为负数的是(?? )
A.?5+(-3)?????????B.?5-(-3)????????C.?5×(-3)??????????????D.?(-5)÷(-3)
7.如图所示,在这个数据运算程序中,如果开始输入的x的值为10,那么第1次输出的结果是5,返回进行第二次运算,那么第2次输出的结果是16,……以此类推,第204次输出的结果是(? )
A.?1?????????????????????B.?2??????????????????????C.?4???????????????????D.?5
8.我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,浔浔在从右到左依次排列的绳子上打结,满七进一,用来记录立志为中考奋斗后努力的天数,由图可知,浔浔努力的天数是(? )
A.?124????????????????????B.?469?????????????????????????C.?67?????????????????????D.?210
9.若a、b互为倒数,则3-4ab的结果为(?? )
A.?-1???????????????????B.?1???????????????????C.?7???????????????????????????D.?-7
10.若a,b互为相反数,c,d互为倒数,则(a+b﹣1)(cd+1)的值是(? )
A.?1??????????????????B.?0???????????????????????C.?﹣1?????????????????????????????D.?﹣2
二、填空题
11.规定*是一种运算符号,且a*b=ab-2a,例1*2=1×2-2×1=0,则4*(-2*3)=________.
12.计算: 6×(-12+23)= ________.
13.计算: 163÷(-117+49-13) = ________ ;
14.如图,是北京S1线地铁的分布示意图,其中桥户营、四道桥、金安桥、苹果园四站在同一条直线上.如果在图中以正东为正方向建立数轴,桥户营站、苹果园站表示的数分别是 -?4 ,2,那么金安桥站表示的数是________.
15.从数-5,1,-3,5,-2中任取三个不同的数相乘,最大的乘积是________,最小的乘积是________.
16.已知 |a|=6 , |b|=3 ,且 a17.“24”点游戏,游戏规则:用一副扑克牌去掉大小王,从中任取4张,将抽出的数进行加减乘除四则运算,使其结果为24,如:1、2、3、4,可运算为 (1+2+3)×4=24 现抽3、-4、2、5,用上述规则写出运算等式使其结果为24,等式可以是________.
18.按下图规律,在第四个方框内填入的数应为________.
三、解答题
19.计算: (1)( 13-16 )×12+|﹣2|; (2)2 23×(-38)-5÷3×13 .
20.计算: (1)-5×2+3÷ 13 -(-1); (2)( -911 )÷ 911-(12-23-34)×(-24) .
21.已知x、y互为相反数,a、b互为倒数,m是最大的负整数,求(x+y)﹣abm的值.
22.以下四个算式通过添加? +? - × ÷及(? )使其成立
①1?? 1? 1? 1? =? 1
②2?? 2? 2? 2? =? 2
③3?? 3? 3? 3? =? 3
④4?? 4? 4? 4? =? 4
23.阅读下列材料:计算 50÷(13-14+112)
解法一:原式= 50÷13-50÷14+50÷112=50×3-50×4+50×12=550 .
解法二:原式= 50÷(13-14+112)=50÷212=50×6=300 .
解法三:原式的倒数为 (13-14+112)÷50=(13-14+112)×150=13×150-14×150+112×150=1300
故原式=300.
上述得出的结果不同,肯定有错误的解法,你认为解法( )是错误的.
请你选择合适的解法解答下列问题:计算: (-142)÷(16-314+23-27)
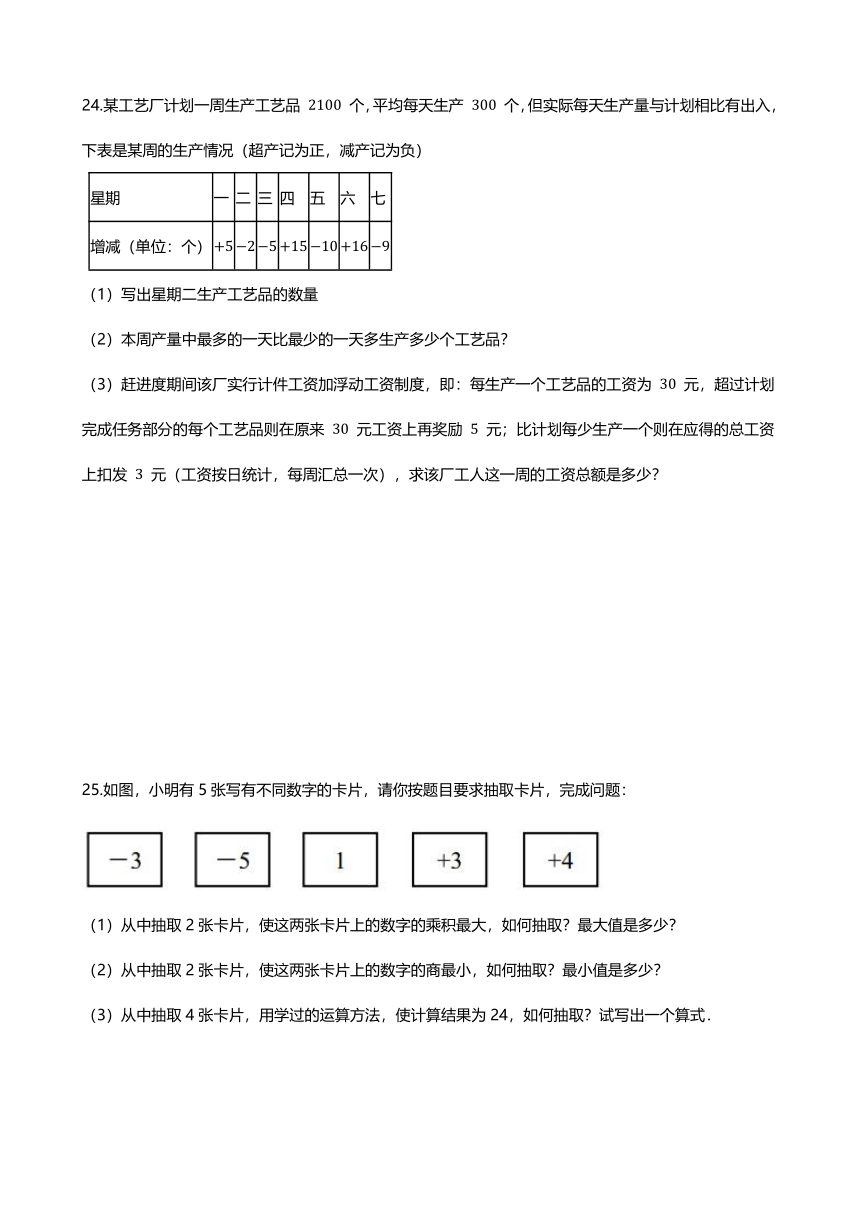
24.某工艺厂计划一周生产工艺品 2100 个,平均每天生产 300 个,但实际每天生产量与计划相比有出入,下表是某周的生产情况(超产记为正,减产记为负)
星期
一
二
三
四
五
六
七
增减(单位:个)
+5
-2
-5
+15
-10
+16
-9
(1)写出星期二生产工艺品的数量
(2)本周产量中最多的一天比最少的一天多生产多少个工艺品?
(3)赶进度期间该厂实行计件工资加浮动工资制度,即:每生产一个工艺品的工资为 30 元,超过计划完成任务部分的每个工艺品则在原来 30 元工资上再奖励 5 元;比计划每少生产一个则在应得的总工资上扣发 3 元(工资按日统计,每周汇总一次),求该厂工人这一周的工资总额是多少?
25.如图,小明有5张写有不同数字的卡片,请你按题目要求抽取卡片,完成问题:
(1)从中抽取2张卡片,使这两张卡片上的数字的乘积最大,如何抽取?最大值是多少?
(2)从中抽取2张卡片,使这两张卡片上的数字的商最小,如何抽取?最小值是多少?
(3)从中抽取4张卡片,用学过的运算方法,使计算结果为24,如何抽取?试写出一个算式.
26.阅读下列材料并解决有关问题:我们知道|x|= {x(x>0)0(x=0)-x(x<0) ,
所以当x>0时, x|x|=xx =1;当x<0时, x|x|=x-x =﹣1.现在我们可以用这个结论来解决下面问题:
(1)已知a,b是有理数,当ab≠0时, a|a|+b|b| =________;
(2)已知a,b,c是有理数,当abc≠0时, a|a|+b|b|+c|c| =________;
(3)已知a,b,c是有理数,a+b+c=0,abc<0,则 b+c|a|+a+c|b|+a+b|c| =________.
答案
一、选择题
1.解:(-8)÷2=-4,
故答案为:B.
2.解: (-3)×(-1)=3 ,
故答案为: C.
3.解:∵有六个数-4,-2,0,1,3,5,
∴三数之积的最大值是(-4)×(-2)×5=40.
故答案为:B.
4.由题意可得,某一个两位数十位数字是a,个位数字是b,将这个两位数乘11,得到一个三位数,
则根据上述的方法可得:
当a+b< 10时,该三位数百位数字是a,十位数字是a + b,个位数字是b,
当a+b≥10时,结果的百位数字是a + 1,十位数字是a+b- 10,个位数字是b.
所以计算结果中十位上的数字可表示为:a+b 或a+b?10.
故答案为:D.
5.解:∵m的相反数是-6,
∴m=6,
∵n的倒数是 13 ,
∴n=3,
∴mn=6×3=18,
故答案为:B.
6.A. 5+(-3) =2,不符合题意,???
B. 5-(-3) =8,不符合题意,???
C. 5×(-3) =-15,符合题意,
D. (-5)÷(-3) = 53 ,不符合题意,
故答案为:C.
7.解:由数据运算程序得,如果开始输入的x的值为10,那么:
第1次输出的结果是5
第2次输出的结果是16
第3次输出的结果是8
第4次输出的结果是4
第5次输出的结果是2
第6次输出的结果是1
第7次输出的结果是4
……
综上可得,从第4次开始,每三个一循环
由 (204-3)÷3=67 可得第204次输出的结果与第6次输出的结果相等
故答案为:A
8.解:根据题意,
4+2×7+1×7×7=4+14+49=67 .
故答案为:C.
9.解:∵a,b互为倒数,
∴ab=1,
则3-4ab=3-4×1=-1.
故答案为:A.
10.解:∵a,b互为相反数,c,d互为倒数,
∴a+b=0,cd=1,
∴(a+b-1)(cd+1)=(0-1)(1+1)=-2.
故答案为:D.
二、填空题
11.解:根据题意得: 4*(-2*3) ?=4×(-2*3)-2×4 =4×[(-2)×3-2×(-2)]-8 =4×[-6-(-4)]-8 =4×(-2)-8 =-8-8 =-16
故答案为:-16.
12.解: 6×(-12+23)
= -12×6+23×6
= -3+4
=1
故答案为:1.
13.解: 163÷(-117+49-13)
= 163÷(-7263+2863-2163)
= 163÷(-6563)
= -163×6365
= -165
故答案为: -165 .
14.∵桥户营站、苹果园站表示的数分别是 -?4 ,2,
∴桥户营站与苹果园站的距离是2-(-4)=6,
∵桥户营站与苹果园站之间共有三个单位长度,
∴每个单位长度表示 6÷3=2 ,
∴金安桥表示的数是2-2=0,
故答案为:0.
15.最大乘积是:(-3)×(-5)×5=75,
最小乘积是:(-2)×(-3)×(-2)=-30,
故答案为:75,-30.
16.解:∵|a|=6,|b|=3,且a<b,
∴a=-6,b=-3或a=-6,b=3,
则原式=18-2=16或-18+2=-16,
故答案为:16或-16.
17.根据题意可得: 2×[5+3-(-4)]=24 或 (-4)×(2-3-5)=24 等,
故答案为:2×[5+3-(-4)]=24(答案不唯一,正确即可)
18.解:∵-1×2×(3+4)=-14,-2×3×(4+5)=-54,
∴第四个方框内填入的数应为-4×5×(6+7)=-260.
故答案为:-260.
三、解答题
19. (1)解:原式= 13×12-16×12 +2
=4-2+2
=4;
(2)解:原式= 83×(-38)-5×13×13
= (-1)-59
= -149 .
20.(1)解:原式=-10+3×3+1=-10+9+1=0,
故答案为:0;
(2)解:原式= -911×119+12×24-23×24-34×24
=-1+12-16-18
=-23 ,
故答案为:-23.
21. 解:∵x、y互为相反数,a、b互为倒数,m是最大的负整数,
∴x+y=0,ab=1,m=-1
∴(x+y)﹣abm=0-1×(-1)=1.
22. 解:①1 × 1 +1﹣1=1;
②2 ÷ 2 +2 ÷2=2;
③3 ×3 ﹣(3 +3)=3;
④4 +( 4﹣4 )×4 = 4.
23. 一;解:上述得出的结果不同,肯定有错误的解法,我认为解法一是错误的;
原式的倒数= (16-314+23-27)÷(-142)=(16-314+23-27)×(-42)
= 16×(-42)+42×314-42×23+42×27=-7+9-28+12=-14 ,
则原式= -114
24. (1)解:周一的产量为: 300+(-2)=298 个;
(2)解:由表格可知:星期六产量最高,为 300+(+16)=316 (个 ) ,
星期五产量最低,为 300+(-10)=290 (个 ) ,
则产量最多的一天比产量最少的一天多生产 316-290=26 (个 ) ;
(3)解: (+5)+(-2)+(-5)+(+15)+(-10)+(+16)+(-9)=10 个,
根据题意得该厂工人一周的工资总额为:
(2100+10)×30+5×5-2×3-5×3+15×5-10×3+16×5-9×3
=63300+25-6-15+75-30+80-27
=63402 (元 ) .
25. (1)解:抽取卡片上的数字是-3和-5的两张卡片,最大值为: (-3)×(-5)=15 ;
(2)解:抽取卡片上的数字是1和-5的两张卡片,这两张卡片上数字的商最小值是: (-5)÷1=-5
(3)解:抽取卡片上的数字是-3,-5,1,+3的四张卡片,算式为: [-5-(+3)]×(-3)×1=24 (答案不唯一).
26. (1)±2或0
(2)±1或±3
(3)﹣1
解:(1)已知a,b是有理数,当ab≠0时,
①a<0,b<0, a|a|+b|b| =-1-1=-2;
②a>0,b>0, a|a|+b|b| =1+1=2;
③a、b异号, a|a|+b|b| =0.
故答案为: ±2或0 ;
( 2 )已知a,b,c是有理数,当abc≠0时,
①a<0,b<0,c<0, a|a|+b|b|+c|c| =-1-1-1=-3;
②a>0,b>0,c>0, a|a|+b|b|+c|c| =1+1+1=3;
③a、b、c两负一正, a|a|+b|b|+c|c| =-1-1+1=-1;
④a、b、c两正一负, a|a|+b|b|+c|c| =-1+1+1=1.
故 a|a|+b|b|+c|c| =±1或±3;
故答案为:±1或±3;
( 3 )已知a,b,c是有理数,a+b+c=0,abc<0,
则b+c=-a,a+c=-b,a+b=-c,a、b、c两正一负,
则 b+c|a|+a+c|b|+a+b|c| ═- a|a|-b|b|-c|c| =1-1-1=-1.
故答案为:-1.
一、选择题
1.计算: (-8)÷2 的结果是(?? )
A.?3?????????????????????B.?4???????????????????????C.?6?????????????????????????D.?16
2.计算(﹣3)×(﹣1)的结果是( )
A.?﹣4?????????????????????B.?﹣3????????????????????????????C.?3??????????????????????????D.?4
3.在-4,-2,0,1,3,5这六个数中,任意三数之积的最大值是(?? )
A.?15??????????????????B.?40???????????????????C.?24???????????????????D.?30
4.(阅读理解)计算: 25×11=275 , 13×11=143 , 48×11=528 , 74×11=814 ,观察算式,我们发现两位数乘11的速算方法:头尾一拉,中间相加,满十进一.
(拓展应用)已知一个两位数,十位上的数字是 a ,个位上的数字是 b ,这个两位数乘11,计算结果中十位上的数字可表示为(?? )
A.?a 或 a+1????????B.?a+b 或 ab??????????????C.?a+b-10????????????D.?a+b 或 a+b-10
5.m 的相反数是 -6 , n 倒数是 13 ,则 mn 的值是(?? )
A.?-18????????????????????B.?18???????????????????????C.?2????????????????????????????D.?-2
6.早在两千多年前,中国人已经开始使用负数,并应用到生产和生活中.中国人使用负数在世界上是首创.下列各式计算结果为负数的是(?? )
A.?5+(-3)?????????B.?5-(-3)????????C.?5×(-3)??????????????D.?(-5)÷(-3)
7.如图所示,在这个数据运算程序中,如果开始输入的x的值为10,那么第1次输出的结果是5,返回进行第二次运算,那么第2次输出的结果是16,……以此类推,第204次输出的结果是(? )
A.?1?????????????????????B.?2??????????????????????C.?4???????????????????D.?5
8.我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,浔浔在从右到左依次排列的绳子上打结,满七进一,用来记录立志为中考奋斗后努力的天数,由图可知,浔浔努力的天数是(? )
A.?124????????????????????B.?469?????????????????????????C.?67?????????????????????D.?210
9.若a、b互为倒数,则3-4ab的结果为(?? )
A.?-1???????????????????B.?1???????????????????C.?7???????????????????????????D.?-7
10.若a,b互为相反数,c,d互为倒数,则(a+b﹣1)(cd+1)的值是(? )
A.?1??????????????????B.?0???????????????????????C.?﹣1?????????????????????????????D.?﹣2
二、填空题
11.规定*是一种运算符号,且a*b=ab-2a,例1*2=1×2-2×1=0,则4*(-2*3)=________.
12.计算: 6×(-12+23)= ________.
13.计算: 163÷(-117+49-13) = ________ ;
14.如图,是北京S1线地铁的分布示意图,其中桥户营、四道桥、金安桥、苹果园四站在同一条直线上.如果在图中以正东为正方向建立数轴,桥户营站、苹果园站表示的数分别是 -?4 ,2,那么金安桥站表示的数是________.
15.从数-5,1,-3,5,-2中任取三个不同的数相乘,最大的乘积是________,最小的乘积是________.
16.已知 |a|=6 , |b|=3 ,且 a17.“24”点游戏,游戏规则:用一副扑克牌去掉大小王,从中任取4张,将抽出的数进行加减乘除四则运算,使其结果为24,如:1、2、3、4,可运算为 (1+2+3)×4=24 现抽3、-4、2、5,用上述规则写出运算等式使其结果为24,等式可以是________.
18.按下图规律,在第四个方框内填入的数应为________.
三、解答题
19.计算: (1)( 13-16 )×12+|﹣2|; (2)2 23×(-38)-5÷3×13 .
20.计算: (1)-5×2+3÷ 13 -(-1); (2)( -911 )÷ 911-(12-23-34)×(-24) .
21.已知x、y互为相反数,a、b互为倒数,m是最大的负整数,求(x+y)﹣abm的值.
22.以下四个算式通过添加? +? - × ÷及(? )使其成立
①1?? 1? 1? 1? =? 1
②2?? 2? 2? 2? =? 2
③3?? 3? 3? 3? =? 3
④4?? 4? 4? 4? =? 4
23.阅读下列材料:计算 50÷(13-14+112)
解法一:原式= 50÷13-50÷14+50÷112=50×3-50×4+50×12=550 .
解法二:原式= 50÷(13-14+112)=50÷212=50×6=300 .
解法三:原式的倒数为 (13-14+112)÷50=(13-14+112)×150=13×150-14×150+112×150=1300
故原式=300.
上述得出的结果不同,肯定有错误的解法,你认为解法( )是错误的.
请你选择合适的解法解答下列问题:计算: (-142)÷(16-314+23-27)
24.某工艺厂计划一周生产工艺品 2100 个,平均每天生产 300 个,但实际每天生产量与计划相比有出入,下表是某周的生产情况(超产记为正,减产记为负)
星期
一
二
三
四
五
六
七
增减(单位:个)
+5
-2
-5
+15
-10
+16
-9
(1)写出星期二生产工艺品的数量
(2)本周产量中最多的一天比最少的一天多生产多少个工艺品?
(3)赶进度期间该厂实行计件工资加浮动工资制度,即:每生产一个工艺品的工资为 30 元,超过计划完成任务部分的每个工艺品则在原来 30 元工资上再奖励 5 元;比计划每少生产一个则在应得的总工资上扣发 3 元(工资按日统计,每周汇总一次),求该厂工人这一周的工资总额是多少?
25.如图,小明有5张写有不同数字的卡片,请你按题目要求抽取卡片,完成问题:
(1)从中抽取2张卡片,使这两张卡片上的数字的乘积最大,如何抽取?最大值是多少?
(2)从中抽取2张卡片,使这两张卡片上的数字的商最小,如何抽取?最小值是多少?
(3)从中抽取4张卡片,用学过的运算方法,使计算结果为24,如何抽取?试写出一个算式.
26.阅读下列材料并解决有关问题:我们知道|x|= {x(x>0)0(x=0)-x(x<0) ,
所以当x>0时, x|x|=xx =1;当x<0时, x|x|=x-x =﹣1.现在我们可以用这个结论来解决下面问题:
(1)已知a,b是有理数,当ab≠0时, a|a|+b|b| =________;
(2)已知a,b,c是有理数,当abc≠0时, a|a|+b|b|+c|c| =________;
(3)已知a,b,c是有理数,a+b+c=0,abc<0,则 b+c|a|+a+c|b|+a+b|c| =________.
答案
一、选择题
1.解:(-8)÷2=-4,
故答案为:B.
2.解: (-3)×(-1)=3 ,
故答案为: C.
3.解:∵有六个数-4,-2,0,1,3,5,
∴三数之积的最大值是(-4)×(-2)×5=40.
故答案为:B.
4.由题意可得,某一个两位数十位数字是a,个位数字是b,将这个两位数乘11,得到一个三位数,
则根据上述的方法可得:
当a+b< 10时,该三位数百位数字是a,十位数字是a + b,个位数字是b,
当a+b≥10时,结果的百位数字是a + 1,十位数字是a+b- 10,个位数字是b.
所以计算结果中十位上的数字可表示为:a+b 或a+b?10.
故答案为:D.
5.解:∵m的相反数是-6,
∴m=6,
∵n的倒数是 13 ,
∴n=3,
∴mn=6×3=18,
故答案为:B.
6.A. 5+(-3) =2,不符合题意,???
B. 5-(-3) =8,不符合题意,???
C. 5×(-3) =-15,符合题意,
D. (-5)÷(-3) = 53 ,不符合题意,
故答案为:C.
7.解:由数据运算程序得,如果开始输入的x的值为10,那么:
第1次输出的结果是5
第2次输出的结果是16
第3次输出的结果是8
第4次输出的结果是4
第5次输出的结果是2
第6次输出的结果是1
第7次输出的结果是4
……
综上可得,从第4次开始,每三个一循环
由 (204-3)÷3=67 可得第204次输出的结果与第6次输出的结果相等
故答案为:A
8.解:根据题意,
4+2×7+1×7×7=4+14+49=67 .
故答案为:C.
9.解:∵a,b互为倒数,
∴ab=1,
则3-4ab=3-4×1=-1.
故答案为:A.
10.解:∵a,b互为相反数,c,d互为倒数,
∴a+b=0,cd=1,
∴(a+b-1)(cd+1)=(0-1)(1+1)=-2.
故答案为:D.
二、填空题
11.解:根据题意得: 4*(-2*3) ?=4×(-2*3)-2×4 =4×[(-2)×3-2×(-2)]-8 =4×[-6-(-4)]-8 =4×(-2)-8 =-8-8 =-16
故答案为:-16.
12.解: 6×(-12+23)
= -12×6+23×6
= -3+4
=1
故答案为:1.
13.解: 163÷(-117+49-13)
= 163÷(-7263+2863-2163)
= 163÷(-6563)
= -163×6365
= -165
故答案为: -165 .
14.∵桥户营站、苹果园站表示的数分别是 -?4 ,2,
∴桥户营站与苹果园站的距离是2-(-4)=6,
∵桥户营站与苹果园站之间共有三个单位长度,
∴每个单位长度表示 6÷3=2 ,
∴金安桥表示的数是2-2=0,
故答案为:0.
15.最大乘积是:(-3)×(-5)×5=75,
最小乘积是:(-2)×(-3)×(-2)=-30,
故答案为:75,-30.
16.解:∵|a|=6,|b|=3,且a<b,
∴a=-6,b=-3或a=-6,b=3,
则原式=18-2=16或-18+2=-16,
故答案为:16或-16.
17.根据题意可得: 2×[5+3-(-4)]=24 或 (-4)×(2-3-5)=24 等,
故答案为:2×[5+3-(-4)]=24(答案不唯一,正确即可)
18.解:∵-1×2×(3+4)=-14,-2×3×(4+5)=-54,
∴第四个方框内填入的数应为-4×5×(6+7)=-260.
故答案为:-260.
三、解答题
19. (1)解:原式= 13×12-16×12 +2
=4-2+2
=4;
(2)解:原式= 83×(-38)-5×13×13
= (-1)-59
= -149 .
20.(1)解:原式=-10+3×3+1=-10+9+1=0,
故答案为:0;
(2)解:原式= -911×119+12×24-23×24-34×24
=-1+12-16-18
=-23 ,
故答案为:-23.
21. 解:∵x、y互为相反数,a、b互为倒数,m是最大的负整数,
∴x+y=0,ab=1,m=-1
∴(x+y)﹣abm=0-1×(-1)=1.
22. 解:①1 × 1 +1﹣1=1;
②2 ÷ 2 +2 ÷2=2;
③3 ×3 ﹣(3 +3)=3;
④4 +( 4﹣4 )×4 = 4.
23. 一;解:上述得出的结果不同,肯定有错误的解法,我认为解法一是错误的;
原式的倒数= (16-314+23-27)÷(-142)=(16-314+23-27)×(-42)
= 16×(-42)+42×314-42×23+42×27=-7+9-28+12=-14 ,
则原式= -114
24. (1)解:周一的产量为: 300+(-2)=298 个;
(2)解:由表格可知:星期六产量最高,为 300+(+16)=316 (个 ) ,
星期五产量最低,为 300+(-10)=290 (个 ) ,
则产量最多的一天比产量最少的一天多生产 316-290=26 (个 ) ;
(3)解: (+5)+(-2)+(-5)+(+15)+(-10)+(+16)+(-9)=10 个,
根据题意得该厂工人一周的工资总额为:
(2100+10)×30+5×5-2×3-5×3+15×5-10×3+16×5-9×3
=63300+25-6-15+75-30+80-27
=63402 (元 ) .
25. (1)解:抽取卡片上的数字是-3和-5的两张卡片,最大值为: (-3)×(-5)=15 ;
(2)解:抽取卡片上的数字是1和-5的两张卡片,这两张卡片上数字的商最小值是: (-5)÷1=-5
(3)解:抽取卡片上的数字是-3,-5,1,+3的四张卡片,算式为: [-5-(+3)]×(-3)×1=24 (答案不唯一).
26. (1)±2或0
(2)±1或±3
(3)﹣1
解:(1)已知a,b是有理数,当ab≠0时,
①a<0,b<0, a|a|+b|b| =-1-1=-2;
②a>0,b>0, a|a|+b|b| =1+1=2;
③a、b异号, a|a|+b|b| =0.
故答案为: ±2或0 ;
( 2 )已知a,b,c是有理数,当abc≠0时,
①a<0,b<0,c<0, a|a|+b|b|+c|c| =-1-1-1=-3;
②a>0,b>0,c>0, a|a|+b|b|+c|c| =1+1+1=3;
③a、b、c两负一正, a|a|+b|b|+c|c| =-1-1+1=-1;
④a、b、c两正一负, a|a|+b|b|+c|c| =-1+1+1=1.
故 a|a|+b|b|+c|c| =±1或±3;
故答案为:±1或±3;
( 3 )已知a,b,c是有理数,a+b+c=0,abc<0,
则b+c=-a,a+c=-b,a+b=-c,a、b、c两正一负,
则 b+c|a|+a+c|b|+a+b|c| ═- a|a|-b|b|-c|c| =1-1-1=-1.
故答案为:-1.
