中考数学复习12 二次函数的图象及其性质

§3.5二次函数的图象及其性质（教 案）
教学目标
1) 正确理解和掌握二次函数的概念、图象和性质
2) 利用数形结合的思想,借助函数的图象和性质形象直观地解决有关不等式最大(小)值、方程的解 以及图形的位置关系等问题.
3）利用转化思想,通过一元二次方程根的判别式及根与系数的来解决抛物线与x轴交点的问题
教学重点与难点
重点：理解和掌握二次函数的概念、图象和性质
难点：数形结合的思想
一．考点知识整合：
考点一 二次函数的概念
一般地，如果＿＿＿＿＿＿＿＿＿＿＿＿（a,b,c是常数,a≠0），那么y叫做x的二次函数。
考点二 二次函数的表达式与图象
1.二次函数的不同表达式
y=ax2(a≠0)的图象顶点为＿＿＿＿,对称轴为＿＿＿＿
y=ax2+k(a≠0)的图象顶点为＿＿＿＿,对称轴为＿＿＿＿
y=a(x-h)2 (a≠0)的图象顶点为＿＿＿＿,对称轴为＿＿＿＿
y=a(x-h)2+k (a≠0)的图象顶点为＿＿＿＿,对称轴为＿＿＿＿
y=ax2+bx+c(a≠0)通过配方化为顶点式为
＿＿＿＿＿＿＿＿＿＿＿＿顶点坐标为＿＿＿＿＿＿＿,对称轴为＿＿＿＿＿＿
考点三 二次函数的平移(a≠0)
上加下减,左加右减
跟进训练:
3.(2010.兰州)抛物线y=x2+bx+c图象向右平移2个单位再向下平移3个单位,所得图象的解析式为y=x2-2x-3,则b,c的值为（ ）
A.b=2,c=3 B.b=2,c=0 C.b=-2,c=-1 D.b=-3,c=2
考点四 二次函数的图象与a,b,c的关系
1.a确定抛物线开口方向,大小和最值:
抛物线开口大小由︱a︱决定,
︱a︱越大,开口越＿＿＿, ︱a︱越小,开口越＿＿＿
当a>0时,图象开口向上,x= ＿＿＿＿时,y有最值＿＿＿＿为＿＿＿＿;
当a<0时,图象开口向下,x= ＿＿＿＿时,y有最值＿＿＿＿为＿＿＿＿
2.a与b共同确定了抛物线的对称轴及其位置:
对称轴为x= ＿＿＿时,当a、b同号时,对称轴与x轴交于＿＿＿半轴;
当a、b异号时,对称轴与x轴交于＿＿＿半轴.
3.C确定抛物线与y轴的交点:
交点坐标为＿＿＿＿,当c>0时,交点位于y轴的＿＿＿＿半轴;
当c<0时,交点位于y轴的＿＿＿＿半轴.
4.a、b、c共同组成△=b2-4ac,其符号确定抛物线与x轴的交点个数
b2-4ac>0时,抛物线与x轴有＿＿＿个交点;
b2-4ac=0时,抛物线与x轴有＿＿＿个交点;
b2-4ac<0时,抛物线与x轴有＿＿＿个交点.
跟进训练:
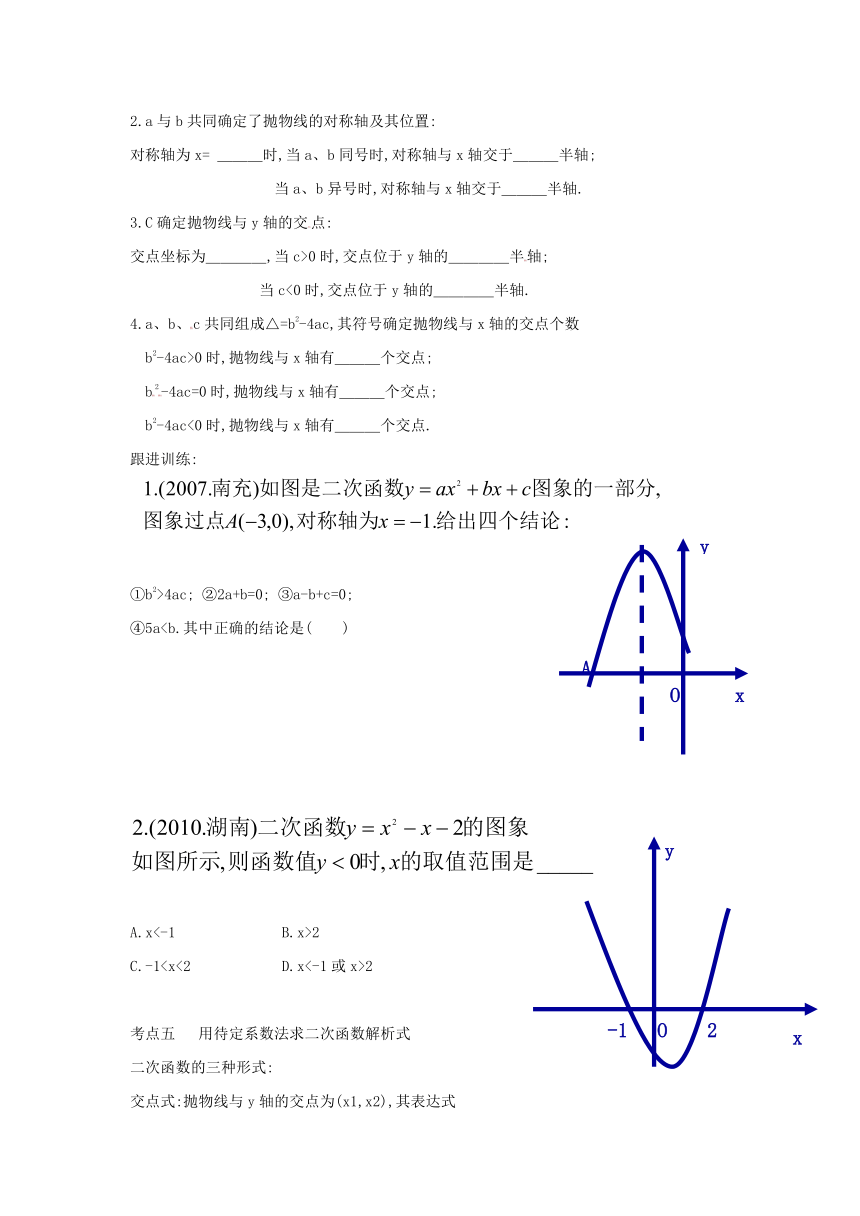
①b2>4ac; ②2a+b=0; ③a-b+c=0;
④5aA.x<-1 B.x>2
C.-12
考点五 用待定系数法求二次函数解析式
二次函数的三种形式:
交点式:抛物线与y轴的交点为(x1,x2),其表达式
可写为＿＿＿＿＿＿＿＿＿＿＿＿
顶点式:顶点坐标为(h, k),其表达式可写为 ＿＿＿＿＿＿＿＿＿＿＿＿
一般式:＿＿＿＿＿＿＿＿＿＿＿＿
归类示例:
例1.(2010.上海)如图,已知平面直角坐标系xoy,抛物线y=-x2+bx+c过点A(4,0) 、B(1,3).
(1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;
(2)记该抛物线的对称轴为直线L,设抛物线上的点P(m,n)在第四象限,点P关于直线L的对称点为E,点E关于x轴的对称点为F,若四边形OAPF的面积为20,求m 、 n的值.
（2）分析：
跟进训练:
(1)若该函数顶点恰为点M,写出此时n的值及y的最大值;
(2)当n=-2时,确定这个二次函数的解析式,并判断此时y是否有最大值;
(3)由(1).(2)可知, n的取值变化,会影响该函数图象的开口方向,请你求出n满足什么条件时, y有最小值
小结:
1.正确理解和掌握二次函数的概念、图象和性质.
2.利用数形结合的思想,借助函数的图象和性质形 象直观地解决有关不等式最大(小)值、方程的解 以及图形的位置关系等问题.
3.利用转化思想,通过一元二次方程根的判别式及根与系数的关系来解决抛物线与x轴交点的问题
A
O
x
y
-1
2
O
x
y
o
y
1
2
3
1
2
3
4
x