广东省广州市中学教学研究会2022届高三上学期6月调研考试数学试题 PDF版含答案
文档属性
| 名称 | 广东省广州市中学教学研究会2022届高三上学期6月调研考试数学试题 PDF版含答案 |  | |
| 格式 | |||
| 文件大小 | 233.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-21 10:40:18 | ||
图片预览



文档简介
2022届广东省广州市中学教学研究会高三调研考试
数 学
注意事项:
1.答卷前,考生务必将自己的姓名、考生号、试室号和座位号填写在答题卡上。
2.用 2B 铅笔将考生号及试卷类型(A)填涂在答题卡相应位置上。作答选择题时,
选出每小题答案后,用 2B 铅笔将答题卡上对应题目选项的答案信息点涂黑;如
需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指
定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不
准使用铅笔和涂改液。不按以上要求作答无效。
4.考生必须保证答题卡的整洁。考试结束后,将试卷和答题卡一并交回。
一、单项选择题:本大题共8小题,每小题5分,满分40分。在每小题给出的四个选项
中,只有一项是符合题目要求的.
⒈ i 为虚数单位,(?1?2 i )?i ?
A.2?i B.2?i C.?2?i D.?2?i
⒉已知向量a ? (2 , 3)与b ? (x , ?6)共线,则x ?
A.?4 B.4 C.9 D.?9
1 3 5 7
⒊一个数列,它的前4项分别是 , , , ,这个数列的一个通项公式是
2 4 8 16
2n?1 2n?1 2n?1 2n?1
A.an ? B.an ? n C.an ? D.an ? n
2n 2 2n 2
4
⒋已知x ? 0,则x? 的
x
A.最大值为2 B.最小值为2 C.最大值为4 D.最小值为4
⒌若 p: f(x)是奇函数,q:y ? f(x)的图象经过坐标原点,则 p是q的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
⒍如图1,正方形SG1G2G3中,E、F 分别是G1G2、G2G3的中点,D是EF 的中
点,沿SE、SF 、EF 将正方形折成一个四面体, S G3
使G1、G2、G3重合,重合后的点记为G,则在
四面体S ?EFG中 F
A.SG ?平面EFG B.SD ?平面EFG D
C.GF ?平面SEF D.GD ?平面SEF G1 E G2
2 2 图1
x y
⒎双曲线C以椭圆 ? ?1的焦点为顶点,以椭圆的顶
16 12
数学试卷第 1 页 共 8 页
点为焦点,则双曲线C的方程为
2 2 2 2 2 2 2 2
x y x y x y x y
A. ? ?1 B. ? ?1 C. ? ?1 D. ? ?1
16 12 4 12 12 4 16 4
⒏一个质量为3kg的物体作直线运动,设运动距离s(单位:m)与时间t(单位:
1
s)的关系可用函数 2 2
s(t) ?1?t 表示,并且物体的动能Ek ? mv .则物体开始
2
运动后第5s时的动能是
75 45
A.150 B.75 C. D.
2 2
二、多项选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项
符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分。
9.已知双曲线E的中心在原点,对称轴为坐标轴,渐近线方程为y ? ?2x,则
双曲线E的离心率为
5 5 3 3 5
A. 2 B. 5 C. 3 D. 5
10.如图是函数 f (x)? Asin(?x??) (?? 0)的部分图象,则
(第10题图)
1 ? 1 ?
f(x)?2sin( x? ) f(x)?2sin( x? )
A. 2 4 B. 2 2
1 ? 1
f(x)??2sin( x? ) f(x)?2cos( x)
C. 2 2 D. 2
11.已知ab?0,则
b a
? ?
2 2 2 2 2
A.a ?b ?2ab B.a ?b ?2ab C.a(a?b)?0 D. a b
?
12.已知随机变量X 的取值为不大于n(n?N )的非负整数,它的概率分布列
为
X 0 1 2 3 … n
p p0 p1 p2 p3 … pn
? ?
其中 pi(i 0,1,2,3,?,n)满足 pi [0,1] ? ?
,且 p0 p1 p2 ??? pn ?1.定义由X 生
数学试卷第 2 页 共 8 页
2 3 i n
? ? ? ?
成的函数 f(x) p0 p1x p2x p3x ??? pix ??? pnx ,g(x)为函数 f(x)的导
函数,E(X)为随机变量X 的期望.现有一枚质地均匀的正四面体型骰子,四个
面分别标有1,2,3,4个点数,这枚骰子连续抛掷两次,向下点数之和为X ,
此时由X 生成的函数为 f1(x),则
15 225
f1(2)? f1(2)?
A.E(X) ? g(2) B. 2 C.E(X) ? g(1) D. 4
三、填空题:本大题共4小题,每小题5分,满分20分.
13.某校在对学生是否喜欢数学的抽样调查中,随机抽取了300名学生,相关的数
据如下表所示:
喜欢数学课程 不喜欢数学课程 总计
男 37 85 122
女 35 143 178
总计 72 228 300
由表中数据直观分析,
该校学生的性别与是否喜欢数学之间________关系(填“有”或“无”).
14.命题 p:每个指数函数都是单调函数,则它的否定?p:________________.
15.若a、b ? 0,则a?b ? 2 ab;若a、b、 3
c ? 0,则a?b?c ?3 abc ;若a、
b、c、 4
d ? 0,则a?b?c?d ? 4 abcd 。猜想:若a1、a2、a3、……、an ? 0,
则________________.
16.如图1,平行六面体ABCD? A1B1C1D1中,AC 与BD
相交于M ,设 AB ? a 、 AD ? b 、 AA1 ? c ,则
⑴B1M ? (用a 、b 、c 表示);
o
⑵若a 、b 、c 三向量是两两成60 角的单位向量,
则| B1M |? .
数学试卷第 3 页 共 8 页
三、解答题:本大题共6小题,满分70分.解答须写出文字说明、证明过程和演算步骤.
17.(本小题满分10分)
在?ABC中,角A、B、C所对应的边分别为a、b、c.
?
⑴若sin(A? ) ? 2cosA,求A的值;
6
1
⑵若cosA? ,b ?3c,求证:?ABC是直角三角形.
3
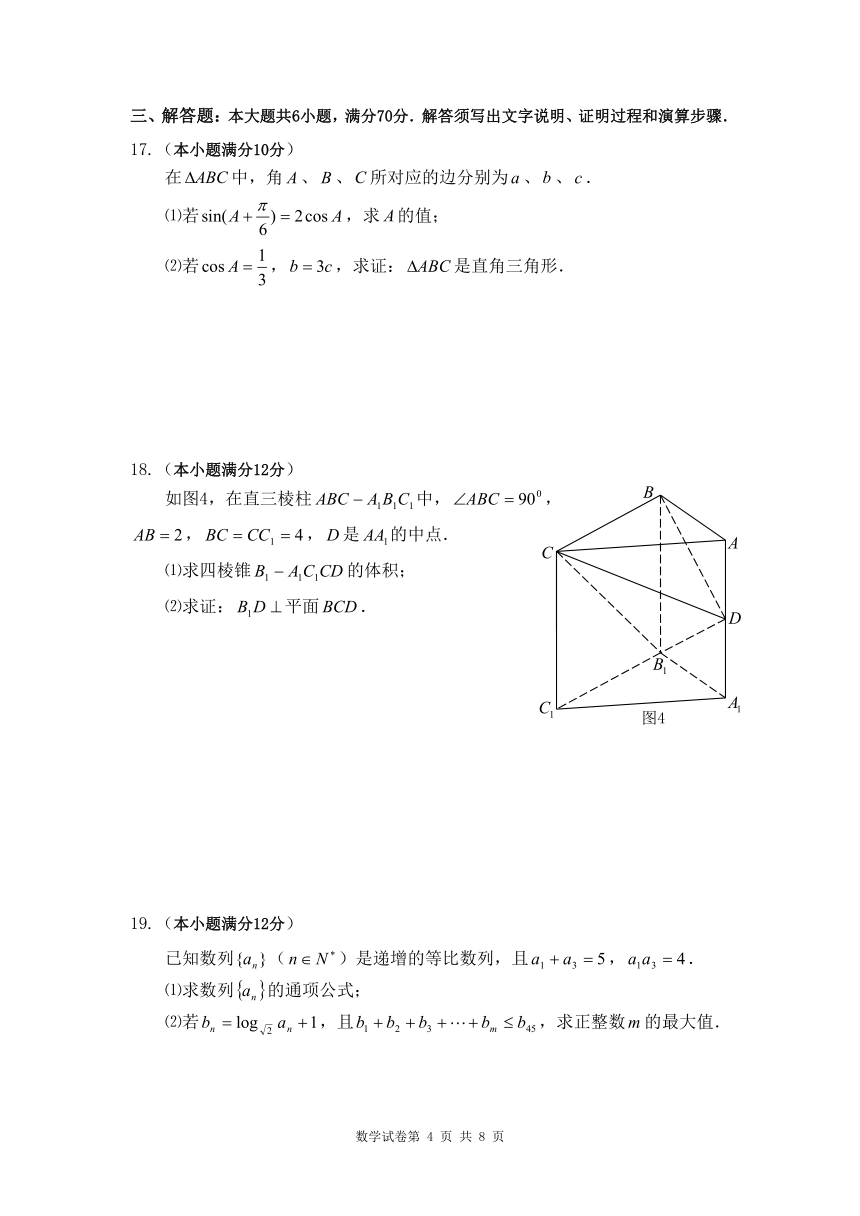
18.(本小题满分12分)
如图4,在直三棱柱 0
ABC ? A B B
1 1C1中,?ABC ?90 ,
AB ? 2,BC ?CC1 ? 4,D是AA1的中点. A
C
⑴求四棱锥B1 ? A1C1CD的体积;
⑵求证:B1D ?平面BCD. D
B1
C A
1 1
图4
19.(本小题满分12分)
?
已知数列{an}(n?N )是递增的等比数列,且a1 ?a3 ?5,a1a3 ? 4.
⑴求数列?an?的通项公式;
⑵若bn ? log 2 an ?1,且b1 ?b2 ?b3 ???bm ?b45,求正整数m的最大值.
数学试卷第 4 页 共 8 页
20.(本小题满分12分)
某次学业水平考试有1000人参加,其成绩的频率分布直方图如图5所示,规
定85分及其以上为优秀.
⑴若成绩在[ 75 , 80)区间有50人,求成绩为优秀的学生人数;
⑵用分层抽样的方法从成绩在[ 80 , 85)和[ 90 , 95)区间的学生中抽取5人进
行研究,问应抽取多少名成绩在[ 90 , 95)区间的学生?
⑶从⑵所抽取的5人中随机抽取2人,求成绩在[ 80 , 85)和[ 90 , 95)区间的学
生恰好各有1人的概率. 频率
组距
0.07
0.06
0.05
0.04
0.03
0.02
0.0O1 75 80 85 90 95 100 分数
图5
21.(本小题满分12分)
2 2
x y 6
已知椭圆C: 2 ? 2 ?1(a ?b ? 0)的一个顶点为A(0, 2),离心率e ? .
a b 3
⑴求椭圆C的方程;
⑵若B是A关于坐标原点的对称点,试探究在椭圆C是否存在点P ,使
?ABP为等腰三角形?若存在,请指出共有几个这样的点?并说明理由(不必具
体求出这些点的坐标).
22.(本小题满分12分)
1 2
已知函数 f(x) ? lnx?(a? )x ,a?R是常数.
2
⑴当a ?1时,求函数 f(x)在区间[ 1,e ]上的最大值和最小值;
⑵若在区间( 1, ??)上,函数 f(x)的图象恒在直线y ? 2ax下方,求实数a的
取值范围.
数学试卷第 5 页 共 8 页
2022届广东省广州市中学教学研究会高三调研考试评分参考
一、单选题 CABDD ABA
二、多选题 AB BCD ACD CD
二、填空题
13.有 14.存在一个指数函数,它不是单调函数(等价表达可相应给分)
1 1
15.a1 ?a2 ?a3 ???a n
n ? n a1a2a3 ???an 16.? a ? b ?c (2分),
2 2
5 (3分)
2
三、解答题
? ? ?
17.⑴由sin(A? ) ? 2cosA得sin Acos ?cosAsin ? 2cosA……2分,所
6 6 6
3 1 3 3
以sin A? ?cosA? ? 2cosA……3分, sin A? cosA,tan A? 3……4
2 2 2 2
?
分,因为0? A??,所以A? ……6分
3
⑵由余弦定理得 2 2 2 2
a ?b ?c ?2bccosA……8分,?8c ……9分,因为
2 2 2 2
a ?c ?9c ?b ……11分,?ABC是直角三角形……12分
18.⑴VB1?A1C1CD ?VABC?A1B1C1 ?VC?ABB1D……1分,
1 1 1 1 1
? ? AB?BC?CC1 ? ?SABB1D ?BC……3分,? ?2?4?4? ? (2?4)?4?2
2 3 2 3 2
……5分,?8……6分
1 1 1
(或:VB1?A1C1CD ? ?SA1C1CD ?h……1分,? ? ?(A1D?C1C)? A1C1?h
3 3 2
1 1 1 1
……2分,? ? ?(A1D?C1C)? A1B1?B1C1……3分,? ? ?(4?2)?2?4……
3 2 3 2
5分,?8……6分)
⑵ABC ? A1B1C1是直三棱柱,所以BB1 ? 底面ABC,BB1 ? BC,又
0
?ABC ?90 ,所以BC ? AB,因为BB1 ? AB ? B,所以BC ?面ABB1A1……7分,
B1D ? 面ABB1A1,所以B1D ? BC ……8分。
数学试卷第 6 页 共 8 页
在 0 0
?ABD中,?BAD ?90 ,AB ? AD ? 2,所以?ADB ? 45 ,同理,
0 0
?A1DB1 ? 45 ……11分,所以?B1DB ?90 ,B1D ? DB……9分。因为
BC?DB ? B,所以B1D ?平面BCD……10分。
19.⑴由a1 ?a3 ?5,a1a3 ? 4解得a1 ?1,a3 ? 4或a1 ? 4,a3 ?1……1分,
因为{an}递增,所以a1 ?1,a3 ? 4……2分。{an}是等比数列,设公比为q,则
2 2
a3 ? a1q ……3分,即4 ?1?q ,解得q ? ?2……4分,因为{an}递增,所以q ? 2
n?1 n?1
……5分,所以数列?an?的通项公式为an ? a1q ? 2 ……6分。
⑵bn ? log 2 an ?1? 2n?1……8分,
1?(2m?1) 2
b1 ?b2 ?b3 ???bm ? ?m ? m
2
……10分,b45 ?89……11分, 2
b1 ?b2 ?b3 ???bm ?b45即m ?89,m ? 89 ,
正整数m的最大值为mmax ?9……12分。
0.07?0.06?0.02
20.⑴依题意,成绩为优秀的学生为 ?50……2分,
0.01
? 750(人)……3分
0.06
⑵应抽取成绩在[ 90 , 95)区间的学生为 ?5……5分,
0.04?0.06
?3(人)……6分
⑶记⑵所抽取的成绩在[ 90 , 95)区间的学生为A1、A2、A3,成绩在[ 80 , 85)
区间的学生为B1、B2,从中随机抽取2人,不同的取法有A1A2、……、B1B2(不
重不漏地列举)……9分,共10种……10分。其中,两区间的学生恰好各有1人的
取法有(不重不漏地列举)……11分,共6种。因为每个取法的可能性相等,所
6 3
以所求概率P ? ? ……12分,
10 5
? c 6
?e ? ?
21.⑴依题意,b ? 2……1分,解? a 3 ……3分,得 2
a ?12……4分,
? 2 2 2
?c ? a ?b
2 2
x y
所以椭圆C的方程为 ? ?1……5分
12 4
⑵依题意B(0, ?2)是椭圆C的下顶点……6分,以AB为底边的等腰三角形
?ABP有两个,此时P 为椭圆C的左右端点……8分;AB是椭圆C的短轴,以A
数学试卷第 7 页 共 8 页
为圆心、AB为半径的圆与椭圆C相交(不含B点)于P1、P2 ,?ABP1、?ABP2
都是等腰三角形……10分;以B为圆心、AB为半径的圆与椭圆C相交(不含A
点)于P3、P4,?ABP3、?ABP4都是等腰三角形……11分;设椭圆C的左右端
点分别为M 、N ,则AM ? 4 ? AB,所以P1、P2 与P3、P4 分别与M 、N 重合,
所以一共存在两个点P ,使?ABP为等腰三角形……12分。
1
22.⑴ 2
a ?1时,f(x) ? lnx? x 在区间[ 1,e ]上单调增加……2分,所以 f(x)
2
2
e 1
在区间[ 1,e ]上的最大值M ? f(e) ?1? ……3分,最小值m ? f(1) ? ……4
2 2
分。
1
⑵记 2
F(x) ? f(x)?2ax ? lnx?(a? )x ?2ax,x?( 1, ??)
2
/ 1 / 2
F (x) ? ?(2a?1)x?2a……5分,由F (x) ? 0得(2a?1)x ?2ax?1? 0
x
1 / 1
若a ? ,则F (x) ? ?1? 0……6分,F(x) ? lnx? x单调递减,
2 x
F(x)? F(1) ? ?1? 0……7分,函数 f(x)的图象恒在直线y ? 2ax下方……8分
1 1 4a 1 2
若a ? ,则a? ? 0,当x ? (?1)时,F(x) ? lnx?(a? )x ?2ax ? 0
2 2 2a?1 2
,函数 f(x)的图象不恒在直线y ? 2ax下方
1 1
若 /
a ? ,F (x) ? (x?1)[(2a?1)? ]? 0……10分,F(x)单调递减,F(x)的
2 x
1 1 1
最大值为F(1) ? ?(a? )……10分,由F(1) ? ?(a? )? 0得a ? ? ……11分。
2 2 2
1 1
综上所述,实数a的取值范围为[? , ]……12分
2 2
数学试卷第 8 页 共 8 页
数 学
注意事项:
1.答卷前,考生务必将自己的姓名、考生号、试室号和座位号填写在答题卡上。
2.用 2B 铅笔将考生号及试卷类型(A)填涂在答题卡相应位置上。作答选择题时,
选出每小题答案后,用 2B 铅笔将答题卡上对应题目选项的答案信息点涂黑;如
需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指
定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不
准使用铅笔和涂改液。不按以上要求作答无效。
4.考生必须保证答题卡的整洁。考试结束后,将试卷和答题卡一并交回。
一、单项选择题:本大题共8小题,每小题5分,满分40分。在每小题给出的四个选项
中,只有一项是符合题目要求的.
⒈ i 为虚数单位,(?1?2 i )?i ?
A.2?i B.2?i C.?2?i D.?2?i
⒉已知向量a ? (2 , 3)与b ? (x , ?6)共线,则x ?
A.?4 B.4 C.9 D.?9
1 3 5 7
⒊一个数列,它的前4项分别是 , , , ,这个数列的一个通项公式是
2 4 8 16
2n?1 2n?1 2n?1 2n?1
A.an ? B.an ? n C.an ? D.an ? n
2n 2 2n 2
4
⒋已知x ? 0,则x? 的
x
A.最大值为2 B.最小值为2 C.最大值为4 D.最小值为4
⒌若 p: f(x)是奇函数,q:y ? f(x)的图象经过坐标原点,则 p是q的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
⒍如图1,正方形SG1G2G3中,E、F 分别是G1G2、G2G3的中点,D是EF 的中
点,沿SE、SF 、EF 将正方形折成一个四面体, S G3
使G1、G2、G3重合,重合后的点记为G,则在
四面体S ?EFG中 F
A.SG ?平面EFG B.SD ?平面EFG D
C.GF ?平面SEF D.GD ?平面SEF G1 E G2
2 2 图1
x y
⒎双曲线C以椭圆 ? ?1的焦点为顶点,以椭圆的顶
16 12
数学试卷第 1 页 共 8 页
点为焦点,则双曲线C的方程为
2 2 2 2 2 2 2 2
x y x y x y x y
A. ? ?1 B. ? ?1 C. ? ?1 D. ? ?1
16 12 4 12 12 4 16 4
⒏一个质量为3kg的物体作直线运动,设运动距离s(单位:m)与时间t(单位:
1
s)的关系可用函数 2 2
s(t) ?1?t 表示,并且物体的动能Ek ? mv .则物体开始
2
运动后第5s时的动能是
75 45
A.150 B.75 C. D.
2 2
二、多项选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项
符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分。
9.已知双曲线E的中心在原点,对称轴为坐标轴,渐近线方程为y ? ?2x,则
双曲线E的离心率为
5 5 3 3 5
A. 2 B. 5 C. 3 D. 5
10.如图是函数 f (x)? Asin(?x??) (?? 0)的部分图象,则
(第10题图)
1 ? 1 ?
f(x)?2sin( x? ) f(x)?2sin( x? )
A. 2 4 B. 2 2
1 ? 1
f(x)??2sin( x? ) f(x)?2cos( x)
C. 2 2 D. 2
11.已知ab?0,则
b a
? ?
2 2 2 2 2
A.a ?b ?2ab B.a ?b ?2ab C.a(a?b)?0 D. a b
?
12.已知随机变量X 的取值为不大于n(n?N )的非负整数,它的概率分布列
为
X 0 1 2 3 … n
p p0 p1 p2 p3 … pn
? ?
其中 pi(i 0,1,2,3,?,n)满足 pi [0,1] ? ?
,且 p0 p1 p2 ??? pn ?1.定义由X 生
数学试卷第 2 页 共 8 页
2 3 i n
? ? ? ?
成的函数 f(x) p0 p1x p2x p3x ??? pix ??? pnx ,g(x)为函数 f(x)的导
函数,E(X)为随机变量X 的期望.现有一枚质地均匀的正四面体型骰子,四个
面分别标有1,2,3,4个点数,这枚骰子连续抛掷两次,向下点数之和为X ,
此时由X 生成的函数为 f1(x),则
15 225
f1(2)? f1(2)?
A.E(X) ? g(2) B. 2 C.E(X) ? g(1) D. 4
三、填空题:本大题共4小题,每小题5分,满分20分.
13.某校在对学生是否喜欢数学的抽样调查中,随机抽取了300名学生,相关的数
据如下表所示:
喜欢数学课程 不喜欢数学课程 总计
男 37 85 122
女 35 143 178
总计 72 228 300
由表中数据直观分析,
该校学生的性别与是否喜欢数学之间________关系(填“有”或“无”).
14.命题 p:每个指数函数都是单调函数,则它的否定?p:________________.
15.若a、b ? 0,则a?b ? 2 ab;若a、b、 3
c ? 0,则a?b?c ?3 abc ;若a、
b、c、 4
d ? 0,则a?b?c?d ? 4 abcd 。猜想:若a1、a2、a3、……、an ? 0,
则________________.
16.如图1,平行六面体ABCD? A1B1C1D1中,AC 与BD
相交于M ,设 AB ? a 、 AD ? b 、 AA1 ? c ,则
⑴B1M ? (用a 、b 、c 表示);
o
⑵若a 、b 、c 三向量是两两成60 角的单位向量,
则| B1M |? .
数学试卷第 3 页 共 8 页
三、解答题:本大题共6小题,满分70分.解答须写出文字说明、证明过程和演算步骤.
17.(本小题满分10分)
在?ABC中,角A、B、C所对应的边分别为a、b、c.
?
⑴若sin(A? ) ? 2cosA,求A的值;
6
1
⑵若cosA? ,b ?3c,求证:?ABC是直角三角形.
3
18.(本小题满分12分)
如图4,在直三棱柱 0
ABC ? A B B
1 1C1中,?ABC ?90 ,
AB ? 2,BC ?CC1 ? 4,D是AA1的中点. A
C
⑴求四棱锥B1 ? A1C1CD的体积;
⑵求证:B1D ?平面BCD. D
B1
C A
1 1
图4
19.(本小题满分12分)
?
已知数列{an}(n?N )是递增的等比数列,且a1 ?a3 ?5,a1a3 ? 4.
⑴求数列?an?的通项公式;
⑵若bn ? log 2 an ?1,且b1 ?b2 ?b3 ???bm ?b45,求正整数m的最大值.
数学试卷第 4 页 共 8 页
20.(本小题满分12分)
某次学业水平考试有1000人参加,其成绩的频率分布直方图如图5所示,规
定85分及其以上为优秀.
⑴若成绩在[ 75 , 80)区间有50人,求成绩为优秀的学生人数;
⑵用分层抽样的方法从成绩在[ 80 , 85)和[ 90 , 95)区间的学生中抽取5人进
行研究,问应抽取多少名成绩在[ 90 , 95)区间的学生?
⑶从⑵所抽取的5人中随机抽取2人,求成绩在[ 80 , 85)和[ 90 , 95)区间的学
生恰好各有1人的概率. 频率
组距
0.07
0.06
0.05
0.04
0.03
0.02
0.0O1 75 80 85 90 95 100 分数
图5
21.(本小题满分12分)
2 2
x y 6
已知椭圆C: 2 ? 2 ?1(a ?b ? 0)的一个顶点为A(0, 2),离心率e ? .
a b 3
⑴求椭圆C的方程;
⑵若B是A关于坐标原点的对称点,试探究在椭圆C是否存在点P ,使
?ABP为等腰三角形?若存在,请指出共有几个这样的点?并说明理由(不必具
体求出这些点的坐标).
22.(本小题满分12分)
1 2
已知函数 f(x) ? lnx?(a? )x ,a?R是常数.
2
⑴当a ?1时,求函数 f(x)在区间[ 1,e ]上的最大值和最小值;
⑵若在区间( 1, ??)上,函数 f(x)的图象恒在直线y ? 2ax下方,求实数a的
取值范围.
数学试卷第 5 页 共 8 页
2022届广东省广州市中学教学研究会高三调研考试评分参考
一、单选题 CABDD ABA
二、多选题 AB BCD ACD CD
二、填空题
13.有 14.存在一个指数函数,它不是单调函数(等价表达可相应给分)
1 1
15.a1 ?a2 ?a3 ???a n
n ? n a1a2a3 ???an 16.? a ? b ?c (2分),
2 2
5 (3分)
2
三、解答题
? ? ?
17.⑴由sin(A? ) ? 2cosA得sin Acos ?cosAsin ? 2cosA……2分,所
6 6 6
3 1 3 3
以sin A? ?cosA? ? 2cosA……3分, sin A? cosA,tan A? 3……4
2 2 2 2
?
分,因为0? A??,所以A? ……6分
3
⑵由余弦定理得 2 2 2 2
a ?b ?c ?2bccosA……8分,?8c ……9分,因为
2 2 2 2
a ?c ?9c ?b ……11分,?ABC是直角三角形……12分
18.⑴VB1?A1C1CD ?VABC?A1B1C1 ?VC?ABB1D……1分,
1 1 1 1 1
? ? AB?BC?CC1 ? ?SABB1D ?BC……3分,? ?2?4?4? ? (2?4)?4?2
2 3 2 3 2
……5分,?8……6分
1 1 1
(或:VB1?A1C1CD ? ?SA1C1CD ?h……1分,? ? ?(A1D?C1C)? A1C1?h
3 3 2
1 1 1 1
……2分,? ? ?(A1D?C1C)? A1B1?B1C1……3分,? ? ?(4?2)?2?4……
3 2 3 2
5分,?8……6分)
⑵ABC ? A1B1C1是直三棱柱,所以BB1 ? 底面ABC,BB1 ? BC,又
0
?ABC ?90 ,所以BC ? AB,因为BB1 ? AB ? B,所以BC ?面ABB1A1……7分,
B1D ? 面ABB1A1,所以B1D ? BC ……8分。
数学试卷第 6 页 共 8 页
在 0 0
?ABD中,?BAD ?90 ,AB ? AD ? 2,所以?ADB ? 45 ,同理,
0 0
?A1DB1 ? 45 ……11分,所以?B1DB ?90 ,B1D ? DB……9分。因为
BC?DB ? B,所以B1D ?平面BCD……10分。
19.⑴由a1 ?a3 ?5,a1a3 ? 4解得a1 ?1,a3 ? 4或a1 ? 4,a3 ?1……1分,
因为{an}递增,所以a1 ?1,a3 ? 4……2分。{an}是等比数列,设公比为q,则
2 2
a3 ? a1q ……3分,即4 ?1?q ,解得q ? ?2……4分,因为{an}递增,所以q ? 2
n?1 n?1
……5分,所以数列?an?的通项公式为an ? a1q ? 2 ……6分。
⑵bn ? log 2 an ?1? 2n?1……8分,
1?(2m?1) 2
b1 ?b2 ?b3 ???bm ? ?m ? m
2
……10分,b45 ?89……11分, 2
b1 ?b2 ?b3 ???bm ?b45即m ?89,m ? 89 ,
正整数m的最大值为mmax ?9……12分。
0.07?0.06?0.02
20.⑴依题意,成绩为优秀的学生为 ?50……2分,
0.01
? 750(人)……3分
0.06
⑵应抽取成绩在[ 90 , 95)区间的学生为 ?5……5分,
0.04?0.06
?3(人)……6分
⑶记⑵所抽取的成绩在[ 90 , 95)区间的学生为A1、A2、A3,成绩在[ 80 , 85)
区间的学生为B1、B2,从中随机抽取2人,不同的取法有A1A2、……、B1B2(不
重不漏地列举)……9分,共10种……10分。其中,两区间的学生恰好各有1人的
取法有(不重不漏地列举)……11分,共6种。因为每个取法的可能性相等,所
6 3
以所求概率P ? ? ……12分,
10 5
? c 6
?e ? ?
21.⑴依题意,b ? 2……1分,解? a 3 ……3分,得 2
a ?12……4分,
? 2 2 2
?c ? a ?b
2 2
x y
所以椭圆C的方程为 ? ?1……5分
12 4
⑵依题意B(0, ?2)是椭圆C的下顶点……6分,以AB为底边的等腰三角形
?ABP有两个,此时P 为椭圆C的左右端点……8分;AB是椭圆C的短轴,以A
数学试卷第 7 页 共 8 页
为圆心、AB为半径的圆与椭圆C相交(不含B点)于P1、P2 ,?ABP1、?ABP2
都是等腰三角形……10分;以B为圆心、AB为半径的圆与椭圆C相交(不含A
点)于P3、P4,?ABP3、?ABP4都是等腰三角形……11分;设椭圆C的左右端
点分别为M 、N ,则AM ? 4 ? AB,所以P1、P2 与P3、P4 分别与M 、N 重合,
所以一共存在两个点P ,使?ABP为等腰三角形……12分。
1
22.⑴ 2
a ?1时,f(x) ? lnx? x 在区间[ 1,e ]上单调增加……2分,所以 f(x)
2
2
e 1
在区间[ 1,e ]上的最大值M ? f(e) ?1? ……3分,最小值m ? f(1) ? ……4
2 2
分。
1
⑵记 2
F(x) ? f(x)?2ax ? lnx?(a? )x ?2ax,x?( 1, ??)
2
/ 1 / 2
F (x) ? ?(2a?1)x?2a……5分,由F (x) ? 0得(2a?1)x ?2ax?1? 0
x
1 / 1
若a ? ,则F (x) ? ?1? 0……6分,F(x) ? lnx? x单调递减,
2 x
F(x)? F(1) ? ?1? 0……7分,函数 f(x)的图象恒在直线y ? 2ax下方……8分
1 1 4a 1 2
若a ? ,则a? ? 0,当x ? (?1)时,F(x) ? lnx?(a? )x ?2ax ? 0
2 2 2a?1 2
,函数 f(x)的图象不恒在直线y ? 2ax下方
1 1
若 /
a ? ,F (x) ? (x?1)[(2a?1)? ]? 0……10分,F(x)单调递减,F(x)的
2 x
1 1 1
最大值为F(1) ? ?(a? )……10分,由F(1) ? ?(a? )? 0得a ? ? ……11分。
2 2 2
1 1
综上所述,实数a的取值范围为[? , ]……12分
2 2
数学试卷第 8 页 共 8 页
同课章节目录
