黑龙江省哈市第九高级中学校2020-2021学年高二下学期6月月考数学(文)试题 Word版含答案
文档属性
| 名称 | 黑龙江省哈市第九高级中学校2020-2021学年高二下学期6月月考数学(文)试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 849.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-21 10:46:28 | ||
图片预览




文档简介
哈尔滨市第九中学2020——2021学年度下学期
6月阶段性评价考试高二学年数学(文)学科试卷
(考试时间:120分钟 满分:150分)
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,每小题给出的四个选项中,只有一项符合题目要求)
1.若false,则false( )
A.false B.false C.false D.false
2.在区间false上随机取一个数false,则false的概率为( )
A.false B.false C.false D.false
3.“双色球”彩票中红色球的号码由编号为false,false,…,false的false个个体组成,一位彩民利用下面的随机数表选取false组数作为false个红色球的编号,选取方法是从随机数表第false行的第false列和第false列数字开始由左到右依次选取两个数字,则选出来的第false个红色球的编号为( )
false false false false false false false false false false false false false false false false false false false false
false false false false false false false false false false false false false false false false false false false false
A.false B.false C.false D.false
4.某城市收集并整理了该市2018年1月份至10月份每月最低气温与最高气温(单位:℃)的数据,绘制了下面的折线图.已知该市每月的最低气温与当月的最高气温两变量具有较好的线性关系,则根据该折线图,下列结论错误的是( )
A.每月的最低气温与当月的最高气温两变量为正相关
B.10月份的最高气温不低于5月份的最高气温
C.月温差(最高气温减最低气温)的最大值出现在1月份
D.最低气温低于false的月份有false个
5.曲线false在点false处的切线的斜率为( )
A.false B.false C.false D.false
6.已知命题false:false,false,若false是假命题,则实数false的取值范围是( )
A.false B.false C.false D.false
7.下列结论正确的是( )
A.命题“若false,则false”的否命题为:“若false,则false”
B.已知false是false上的可导函数,则“false”是“false是函数false的极值点”的充分不必要条件
C.若false为真命题,false为假命题,则false为真命题
D.若false,则“false”是“false”的充要条件
8.某网店经销某商品,为了解该商品的月销量false(单位:千件)与售价false(单位:元/件)之间的关系,收集false组数据进行了初步处理,得到如下数表:
false
false
false
false
false
false
false
false
false
false
false
false
根据表中的数据可得回归直线方程false,以下说法正确的是( )
A.false,false具有负相关关系,相关系数false
B.false每增加一个单位,false平均减少false个单位
C.第二个样本点对应的残差false
D.第三个样本点对应的残差false
9.已知具有相关关系的两个随机变量的一组观测数据的散点图分布在函数false的图象附近,设false,将其变换后得到线性方程false,则false( )
A.false B.false C.false D.false
10.下列叙述错误的是( )
A.互斥事件不一定是对立事件,但是对立事件一定是互斥事件
B.甲、乙两人下棋,两人下成和棋的概率为,甲获胜的概率是false,则甲不输的概率为false
C.从装有false个红球和false个黑球的口袋内任取false个球,至少有一个黑球与至少有一个红球是两个互斥而不对立的事件
D.在false件产品中,有false件一等品和false件二等品,从中任取false件,那么事件“至多一件一等品”的概率为false
11.已知定义域为false的奇函数false的导函数为false,当false时,false,若false,false,false,则false,false,false的大小关系正确的是( )
A.false B.false C.false D.false
12.关于函数false,下列说法错误的是( )
A.false是false的极小值点
B.函数false有且只有false个零点
C.存在正实数false,使得false恒成立
D.对任意两个正实数false,false,且false,若false,则false
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4道小题,每小题5分,共20分)
13.某单位有false名职工,现采用系统抽样抽取false人做问卷调查,将false人按false,false,…,false随机编号,则抽取的false人中,编号落入区间false的人数为______.
14.圣宋元宝,是中国古代钱币之一,宋徽宗赵估建中靖国元年(公元101年)始铸,是仁宗“皇宋通宝”之后又一种不以年号命名的非年号钱,种类主要有小平和折二两种.小明同学珍藏有小平钱false枚,折二钱false枚,现随机抽取false枚赠好友,则赠送的两枚为不同种类的概率为_________.
15.现有一块边长为false的正方形铁片,铁片的四角截去四个边长均为falsefalse的小正方形,然后做成一个无盖方盒,该方盒容积的最大值是______.
16.若函数false的最大值为false,则实数false的取值范围为______.
三、解答题(本大题共6小题,共70分)
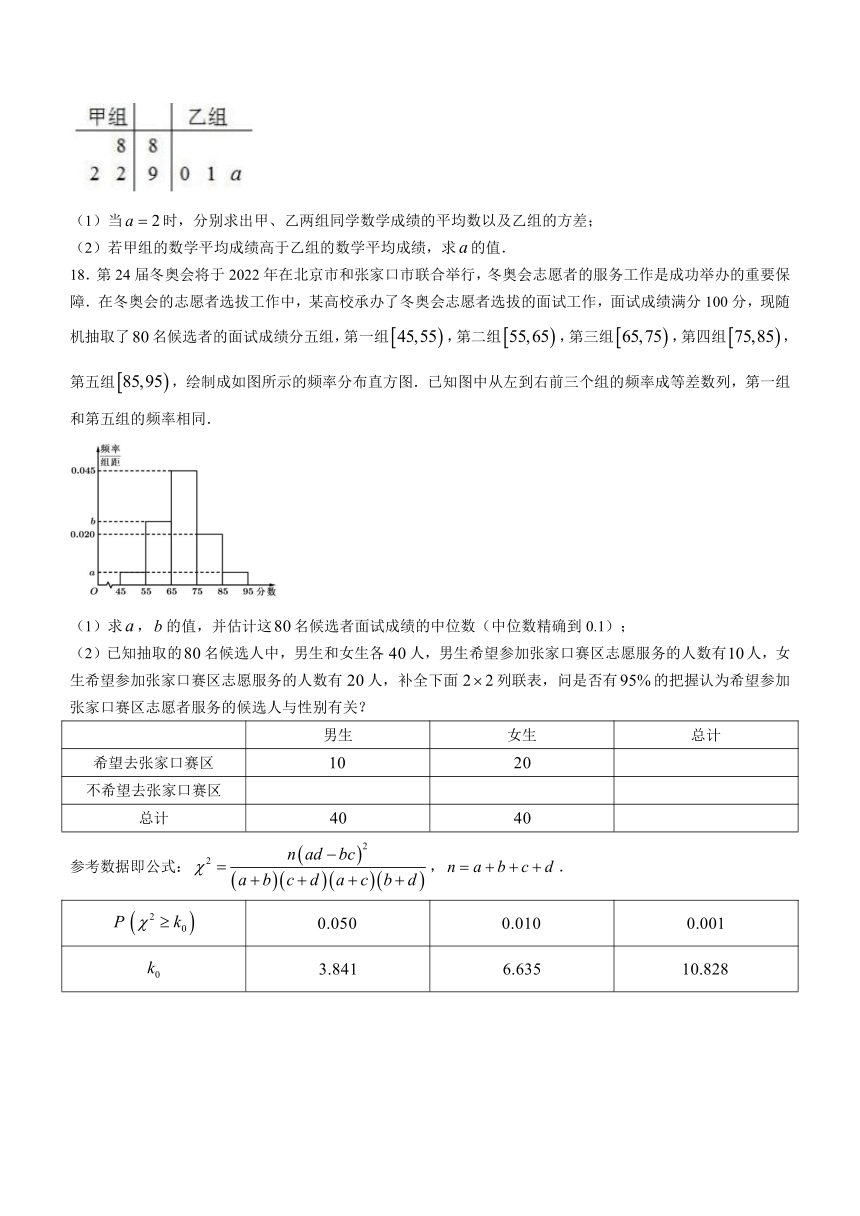
17.以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以false表示.
(1)当false时,分别求出甲、乙两组同学数学成绩的平均数以及乙组的方差;
(2)若甲组的数学平均成绩高于乙组的数学平均成绩,求false的值.
18.第24届冬奥会将于2022年在北京市和张家口市联合举行,冬奥会志愿者的服务工作是成功举办的重要保障.在冬奥会的志愿者选拔工作中,某高校承办了冬奥会志愿者选拔的面试工作,面试成绩满分100分,现随机抽取了false名候选者的面试成绩分五组,第一组false,第二组false,第三组false,第四组false,第五组false,绘制成如图所示的频率分布直方图.已知图中从左到右前三个组的频率成等差数列,第一组和第五组的频率相同.
(1)求false,false的值,并估计这false名候选者面试成绩的中位数(中位数精确到0.1);
(2)已知抽取的false名候选人中,男生和女生各false人,男生希望参加张家口赛区志愿服务的人数有false人,女生希望参加张家口赛区志愿服务的人数有false人,补全下面false列联表,问是否有false的把握认为希望参加张家口赛区志愿者服务的候选人与性别有关?
男生
女生
总计
希望去张家口赛区
false
false
不希望去张家口赛区
总计
false
false
参考数据即公式:false,false.
falsefalse
false
false
false
false
false
false
false
19.在直角坐标系false中,曲线false的参数方程为false(false为参数),圆false的方程为false,以原点false为极点,false轴的非负半轴为极轴且取相等的长度单位建立极坐标系,射线false的极坐标方程为falsefalse.
(1)求曲线false和false的极坐标方程;
(2)当false时,若射线false与曲线false和圆false分别交于异于点false的false、false两点,且false,求false的面积.
20.某商场对false商品近false天的销售情况进行整理,得到如下数据,经统计分析,日销售量false(件)与时间false(天)之间具有线性相关关系.
时间(false)
false
false
false
false
false
日销售量(false)
false
false
false
false
false
(1)请根据表格提供的数据,用最小二乘法原理求出false关于false的线性回归方程false.
(2)已知false商品近false天内的日销售价格false(元)与时间false(天)的关系为falsefalse.根据(1)中求出的线性回归方程,预测false为何值时,false商品的日销售额最大.
参考公式false,false;参考数据:false,false.
21.设函数falsefalse.
(1)求false的单调区间;
(2)若false,false为整数,且当false时,false,求false的最大值.
22.已知函数falsefalse.
(1)当false时,求false在false的零点个数;
(2)若false有两个零点false,false,且false,证明:false.
6月月考答案(理数)
1-12 falsefalsefalsefalsefalse falsefalsefalsefalsefalse falsefalse
13-16 false false false false
17.解:(1)false,false,false
(2)因为甲组false,false,且知false,
所以false,
所以false.
18.解:(1)由题意可知:false,false
解得false,false,
所以中位数等于false
(2)补全false列联表:
男生
女生
总计
希望去张家口赛区
false
false
false
不希望去张家口赛区
false
false
false
总计
false
false
false
false
所以有false的把握认为希望参加张家口赛区志愿者服务的候选人与性别有关.
19.解:(1)由曲线false的参数方程为false(false为参数),消去参数false,
可得曲线false的普通方程为:false,
又false,false,
代入可得false,
false曲线false的极坐标方程:false;
由圆false的方程为false,
得false,
falsefalse,得曲线false的极坐标方程:false;
(2)falsefalse,
falsefalse,即false,
整理得false,且false,
解得:false,false,false,
点false到false的距离false,
falsefalse的面积为:falsefalse.
20.(1)根据题意,计算false,
false;
false,
false,
所以回归系数为:false,false,
故所求的线性回归方程为false.
(2)由题意日销售额为false;
当false,false时,false;
所以当false时,false(元);
当false,false时,false;
所以当false时,false(元).
综上所述,估计当false天时,false商品日销售额最大值为false元.
21.(1)false,false
当false时,false,
falsefalse在false单调递增;
当false时,由false得:false,
由false得:false,
falsefalse在false单调递减,false单调递增.
综上所述:当false时,false的单调增区间为false,无单调减区间;
当false时,false的单调增区间为false,单调减区间为false.
(2)由于false时,false
故false时,false等价于falsefalse
令false
false在false上单调递增.
false,false,
所以false在false上存在唯一零点,
即false在false上存在唯一零点,
设此零点为false,则false,
当false时,false,
当false时,false,
所以false,
因为false,
所以false,
所以false,
所以整数false的最大值为false.
22.(1)false时,false,false
false在false,false在false,
所以false在false,在false,
false,false,false,
所以存在false,false,
存在false,false
所以false时,false在false上有两个零点,
(2)证明:因为false有两个零点,
所以false,即false.
设false,
则要证false,
因为false,false
又因为false在false上单调递增,
所以只要证false
设falsefalse
则false
所以false在false上单调递减,false,
所以false.
因为false有两个零点,
所以false,即false.
设false,则要证false,
因为false,false
又因为false在false上单调递增,
所以只要证false
设falsefalse
则false
所以false在false上单调递减,false,
所以false.
6月阶段性评价考试高二学年数学(文)学科试卷
(考试时间:120分钟 满分:150分)
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,每小题给出的四个选项中,只有一项符合题目要求)
1.若false,则false( )
A.false B.false C.false D.false
2.在区间false上随机取一个数false,则false的概率为( )
A.false B.false C.false D.false
3.“双色球”彩票中红色球的号码由编号为false,false,…,false的false个个体组成,一位彩民利用下面的随机数表选取false组数作为false个红色球的编号,选取方法是从随机数表第false行的第false列和第false列数字开始由左到右依次选取两个数字,则选出来的第false个红色球的编号为( )
false false false false false false false false false false false false false false false false false false false false
false false false false false false false false false false false false false false false false false false false false
A.false B.false C.false D.false
4.某城市收集并整理了该市2018年1月份至10月份每月最低气温与最高气温(单位:℃)的数据,绘制了下面的折线图.已知该市每月的最低气温与当月的最高气温两变量具有较好的线性关系,则根据该折线图,下列结论错误的是( )
A.每月的最低气温与当月的最高气温两变量为正相关
B.10月份的最高气温不低于5月份的最高气温
C.月温差(最高气温减最低气温)的最大值出现在1月份
D.最低气温低于false的月份有false个
5.曲线false在点false处的切线的斜率为( )
A.false B.false C.false D.false
6.已知命题false:false,false,若false是假命题,则实数false的取值范围是( )
A.false B.false C.false D.false
7.下列结论正确的是( )
A.命题“若false,则false”的否命题为:“若false,则false”
B.已知false是false上的可导函数,则“false”是“false是函数false的极值点”的充分不必要条件
C.若false为真命题,false为假命题,则false为真命题
D.若false,则“false”是“false”的充要条件
8.某网店经销某商品,为了解该商品的月销量false(单位:千件)与售价false(单位:元/件)之间的关系,收集false组数据进行了初步处理,得到如下数表:
false
false
false
false
false
false
false
false
false
false
false
false
根据表中的数据可得回归直线方程false,以下说法正确的是( )
A.false,false具有负相关关系,相关系数false
B.false每增加一个单位,false平均减少false个单位
C.第二个样本点对应的残差false
D.第三个样本点对应的残差false
9.已知具有相关关系的两个随机变量的一组观测数据的散点图分布在函数false的图象附近,设false,将其变换后得到线性方程false,则false( )
A.false B.false C.false D.false
10.下列叙述错误的是( )
A.互斥事件不一定是对立事件,但是对立事件一定是互斥事件
B.甲、乙两人下棋,两人下成和棋的概率为,甲获胜的概率是false,则甲不输的概率为false
C.从装有false个红球和false个黑球的口袋内任取false个球,至少有一个黑球与至少有一个红球是两个互斥而不对立的事件
D.在false件产品中,有false件一等品和false件二等品,从中任取false件,那么事件“至多一件一等品”的概率为false
11.已知定义域为false的奇函数false的导函数为false,当false时,false,若false,false,false,则false,false,false的大小关系正确的是( )
A.false B.false C.false D.false
12.关于函数false,下列说法错误的是( )
A.false是false的极小值点
B.函数false有且只有false个零点
C.存在正实数false,使得false恒成立
D.对任意两个正实数false,false,且false,若false,则false
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4道小题,每小题5分,共20分)
13.某单位有false名职工,现采用系统抽样抽取false人做问卷调查,将false人按false,false,…,false随机编号,则抽取的false人中,编号落入区间false的人数为______.
14.圣宋元宝,是中国古代钱币之一,宋徽宗赵估建中靖国元年(公元101年)始铸,是仁宗“皇宋通宝”之后又一种不以年号命名的非年号钱,种类主要有小平和折二两种.小明同学珍藏有小平钱false枚,折二钱false枚,现随机抽取false枚赠好友,则赠送的两枚为不同种类的概率为_________.
15.现有一块边长为false的正方形铁片,铁片的四角截去四个边长均为falsefalse的小正方形,然后做成一个无盖方盒,该方盒容积的最大值是______.
16.若函数false的最大值为false,则实数false的取值范围为______.
三、解答题(本大题共6小题,共70分)
17.以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以false表示.
(1)当false时,分别求出甲、乙两组同学数学成绩的平均数以及乙组的方差;
(2)若甲组的数学平均成绩高于乙组的数学平均成绩,求false的值.
18.第24届冬奥会将于2022年在北京市和张家口市联合举行,冬奥会志愿者的服务工作是成功举办的重要保障.在冬奥会的志愿者选拔工作中,某高校承办了冬奥会志愿者选拔的面试工作,面试成绩满分100分,现随机抽取了false名候选者的面试成绩分五组,第一组false,第二组false,第三组false,第四组false,第五组false,绘制成如图所示的频率分布直方图.已知图中从左到右前三个组的频率成等差数列,第一组和第五组的频率相同.
(1)求false,false的值,并估计这false名候选者面试成绩的中位数(中位数精确到0.1);
(2)已知抽取的false名候选人中,男生和女生各false人,男生希望参加张家口赛区志愿服务的人数有false人,女生希望参加张家口赛区志愿服务的人数有false人,补全下面false列联表,问是否有false的把握认为希望参加张家口赛区志愿者服务的候选人与性别有关?
男生
女生
总计
希望去张家口赛区
false
false
不希望去张家口赛区
总计
false
false
参考数据即公式:false,false.
falsefalse
false
false
false
false
false
false
false
19.在直角坐标系false中,曲线false的参数方程为false(false为参数),圆false的方程为false,以原点false为极点,false轴的非负半轴为极轴且取相等的长度单位建立极坐标系,射线false的极坐标方程为falsefalse.
(1)求曲线false和false的极坐标方程;
(2)当false时,若射线false与曲线false和圆false分别交于异于点false的false、false两点,且false,求false的面积.
20.某商场对false商品近false天的销售情况进行整理,得到如下数据,经统计分析,日销售量false(件)与时间false(天)之间具有线性相关关系.
时间(false)
false
false
false
false
false
日销售量(false)
false
false
false
false
false
(1)请根据表格提供的数据,用最小二乘法原理求出false关于false的线性回归方程false.
(2)已知false商品近false天内的日销售价格false(元)与时间false(天)的关系为falsefalse.根据(1)中求出的线性回归方程,预测false为何值时,false商品的日销售额最大.
参考公式false,false;参考数据:false,false.
21.设函数falsefalse.
(1)求false的单调区间;
(2)若false,false为整数,且当false时,false,求false的最大值.
22.已知函数falsefalse.
(1)当false时,求false在false的零点个数;
(2)若false有两个零点false,false,且false,证明:false.
6月月考答案(理数)
1-12 falsefalsefalsefalsefalse falsefalsefalsefalsefalse falsefalse
13-16 false false false false
17.解:(1)false,false,false
(2)因为甲组false,false,且知false,
所以false,
所以false.
18.解:(1)由题意可知:false,false
解得false,false,
所以中位数等于false
(2)补全false列联表:
男生
女生
总计
希望去张家口赛区
false
false
false
不希望去张家口赛区
false
false
false
总计
false
false
false
false
所以有false的把握认为希望参加张家口赛区志愿者服务的候选人与性别有关.
19.解:(1)由曲线false的参数方程为false(false为参数),消去参数false,
可得曲线false的普通方程为:false,
又false,false,
代入可得false,
false曲线false的极坐标方程:false;
由圆false的方程为false,
得false,
falsefalse,得曲线false的极坐标方程:false;
(2)falsefalse,
falsefalse,即false,
整理得false,且false,
解得:false,false,false,
点false到false的距离false,
falsefalse的面积为:falsefalse.
20.(1)根据题意,计算false,
false;
false,
false,
所以回归系数为:false,false,
故所求的线性回归方程为false.
(2)由题意日销售额为false;
当false,false时,false;
所以当false时,false(元);
当false,false时,false;
所以当false时,false(元).
综上所述,估计当false天时,false商品日销售额最大值为false元.
21.(1)false,false
当false时,false,
falsefalse在false单调递增;
当false时,由false得:false,
由false得:false,
falsefalse在false单调递减,false单调递增.
综上所述:当false时,false的单调增区间为false,无单调减区间;
当false时,false的单调增区间为false,单调减区间为false.
(2)由于false时,false
故false时,false等价于falsefalse
令false
false在false上单调递增.
false,false,
所以false在false上存在唯一零点,
即false在false上存在唯一零点,
设此零点为false,则false,
当false时,false,
当false时,false,
所以false,
因为false,
所以false,
所以false,
所以整数false的最大值为false.
22.(1)false时,false,false
false在false,false在false,
所以false在false,在false,
false,false,false,
所以存在false,false,
存在false,false
所以false时,false在false上有两个零点,
(2)证明:因为false有两个零点,
所以false,即false.
设false,
则要证false,
因为false,false
又因为false在false上单调递增,
所以只要证false
设falsefalse
则false
所以false在false上单调递减,false,
所以false.
因为false有两个零点,
所以false,即false.
设false,则要证false,
因为false,false
又因为false在false上单调递增,
所以只要证false
设falsefalse
则false
所以false在false上单调递减,false,
所以false.
同课章节目录
