江苏省无锡市锡山区高中2020-2021学年高二下学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 江苏省无锡市锡山区高中2020-2021学年高二下学期期末考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 926.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-21 10:50:04 | ||
图片预览




文档简介
1258570011976100锡山高级中学2020~2021学年度第二学期期末检测
高二年级数学试题
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
4.本卷共6页,满分150分,考试时间120分钟.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.
1.已知false,false均为集合false的子集,且false,false,则false
A.false B.false C.false D.false
2.已知复数false,则以下命题中为真命题的是
A.false的共轭复数为false B.false的虚部为false
C.false D.false在复平面内对应的点在第一象限
3.已知向量false,false,false,且false,false,则false
A.3 B.false C.false D.false
4.围棋起源于中国,据先秦典籍《世本》记载:“尧造围棋,丹朱善之”,至今已有四千多年历史,围棋不仅能抒发意境、陶冶情操、修身养性、生慧增智,而且还与天象易理、兵法策略、治国安邦等相关联,蕴含着中华文化的丰富内涵在某次国际围棋比赛中,甲、乙两人进入最后决赛比赛采取五局三胜制,即先胜三局的一方获得比赛冠军,比赛结束.假设每局比赛甲胜乙的概率都为false,且各局比赛的胜负互不影响,则在不超过4局的比赛中甲获得冠军的概率为
A.false B.false C.false D.false
5.已知数列false的前false项和为false,若false,false,false,false为等差数列,则false
A.false B.false C.false D.false
6.函数false,false的值域是
A.false B.false C.false D.false
7.数学中的数形结合也可以组成世间万物的绚丽画面,一些优美的曲线是数学形象美、对称美、和谐美的产物,曲线false为四叶玫瑰线,下列结论正确的有
(1)方程false,表示的曲线在第二和第四象限;
(2)曲线false上任一点到坐标原点false的距离都不超过2;
(3)曲线false构成的四叶玫瑰线面积大于false;
(4)曲线false上有5个整点(横、纵坐标均为整数的点);
A.(1)(2) B.(1)(2)(3) C.(1)(2)(4) D.(1)(3)(4)
8.若函数false与函数false有公切线,则实数false的取值范围是
A.false B.false C.false D.false
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”过去10日,甲、乙、丙、丁四地新增疑似病例数据信息如下:
甲地:中位数为2,极差为5;
乙地:总体平均数为2,众数为2;
丙地:总体平均数为1,总体方差大于0;
丁地:总体平均数为2,总体方差为3.
则甲、乙、丙、丁四地中,一定没有发生大规模群体感染的有
A.甲地 B.乙地 C.丙地 D.丁地
10.如图,已知函数false(其中false,false,false)的图象与false轴交于点false,false,与false轴交于点false,false,false,false,false.则下列说法正确的有
A.false的最小正周期为12 B.false
C.false的最大值为false D.false在区间false上单调递增
11.已知点false,圆false,点false在圆false上运动,给出下列命题,其中正确的有
A.false的取值范围是false
B.在false轴上存在定点false,使false为定值;
C.设线段false的中点为false,则点false到直线false的距离的取值范围是false;
D.过直线false上一点false引圆false的两条切线,切点分别为false,false,则false的取值范围是false
12.在边长为2的等边三角形false中,点false,false分别是边false,false上的点,满足false且false,将false沿直线false折到false的位置.在翻折过程中,下列结论不成立的是
A.在边false上存在点false,使得在翻折过程中,满足false平面false
B.存在false,使得在翻折过程中的某个位置,满足平面false平面false
C.若false,当二面角false为直二面角时,false
D.在翻折过程中,四棱锥false体积的最大值记为false,false的最大值为false
三、填空题:本题共4小题,每小题5分,共20分.
13.false,false是两条不同的直线,false垂直于平面false,则“false”是“false”的__________条件.
14.已知椭圆false的一个焦点与抛物线false的焦点重合,过点false且斜率为false的直线交椭圆false于false,false两点,若false是线段false的中点,则椭圆false的方程为____________.
15.早期的毕达哥拉斯学派学者注意到:用等边三角形或正方形为表面可构成四种规则的立体图形,即正四面体、正六面体、正八面体和正二十面体,它们的各个面和多面角都全等.如图,正二十面体是由20个等边三角形组成的正多面体,共有12个顶点,30条棱,20个面,是五个柏拉图多面体之一.如果把false按false计算,则该正二十面体的表面积与该正二十面体的外接球表面积之比等于_____________.
16.某校学生在研究民间剪纸艺术时,发现剪纸时经常会沿纸的某条对称轴把纸对折.规格为false的长方形纸,对折1次共可以得到false,false两种规格的图形,它们的面积之和false,对折2次共可以得到false,false,false三种规格的图形,它们的面积之和false,以此类推.则对折4次共可以得到不同规格图形的种数为______________;如果对折false次,那么false____________false.(第1空2分,第2空3分)
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)已知false的内角false,false,false所对的边分别为false,false,false且满足false.
(1)求角false;
(2)设点false在边false上,且false,证明:若_____________,则false存在最大值或最小值.
请在下面的两个条件中选择一个条件填到上面的横线上,并证明.
①false是false的中线;
②false是false的角平分线.
18.(本小题满分12分)设数列false的前false项和为false,满足:false.
(1)求证:数列false为等比数列;
(2)求false,并求false的最大值.
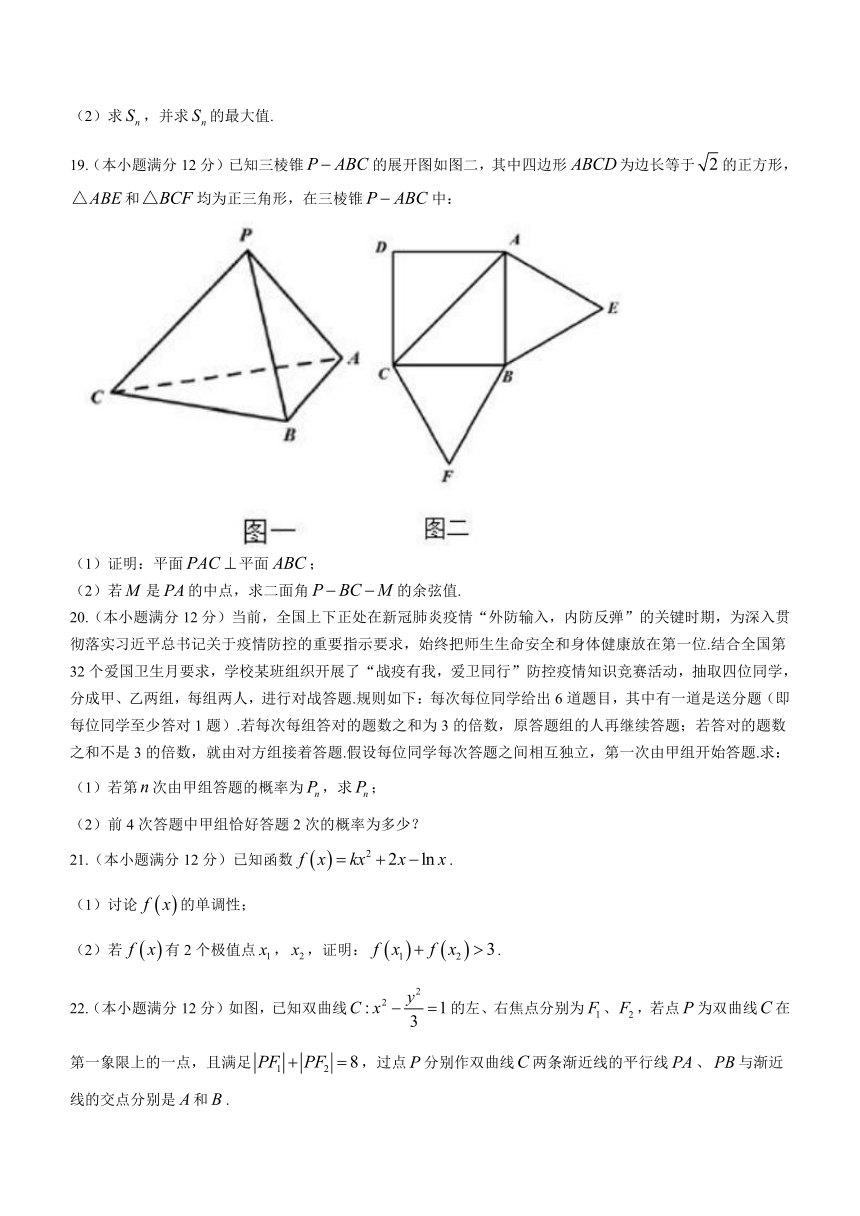
19.(本小题满分12分)已知三棱锥false的展开图如图二,其中四边形false为边长等于false的正方形,false和false均为正三角形,在三棱锥false中:
(1)证明:平面false平面false;
(2)若false是false的中点,求二面角false的余弦值.
20.(本小题满分12分)当前,全国上下正处在新冠肺炎疫情“外防输入,内防反弹”的关键时期,为深入贯彻落实习近平总书记关于疫情防控的重要指示要求,始终把师生生命安全和身体健康放在第一位.结合全国第32个爱国卫生月要求,学校某班组织开展了“战疫有我,爱卫同行”防控疫情知识竞赛活动,抽取四位同学,分成甲、乙两组,每组两人,进行对战答题.规则如下:每次每位同学给出6道题目,其中有一道是送分题(即每位同学至少答对1题).若每次每组答对的题数之和为3的倍数,原答题组的人再继续答题;若答对的题数之和不是3的倍数,就由对方组接着答题.假设每位同学每次答题之间相互独立,第一次由甲组开始答题.求:
(1)若第false次由甲组答题的概率为false,求false;
(2)前4次答题中甲组恰好答题2次的概率为多少?
21.(本小题满分12分)已知函数false.
(1)讨论false的单调性;
(2)若false有2个极值点false,false,证明:false.
22.(本小题满分12分)如图,已知双曲线false的左、右焦点分别为false、false,若点false为双曲线false在第一象限上的一点,且满足false,过点false分别作双曲线false两条渐近线的平行线false、false与渐近线的交点分别是false和false.
(1)求四边形false的面积;
(2)若对于更一般的双曲线false,点false为双曲线false上任意一点,过点false分别作双曲线false两条渐近线的平行线false、false与渐近线的交点分别是false和false.请问四边形false的面积为定值吗?若是定值,求出该定值(用false、false表示该定值);若不是定值,请说明理由.
锡山高级中学2020~2021学年度第二学期期末检测
高二数学参考答案及评分标准
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
D
B
C
D
B
A
A
AD
ACD
BD
ABC
三、填空题:本题共4小题,每小题5分,共20分.
13.必要不充分条件 14.false 15.false 16.(1)5 (2)false
评分细则:13题严格按照答案,一点都不能变.写的潦草的不能得分
14题写成false也算对
15题不化简不得分
16题(1)2分,(2)3分.(2)中形式不唯一,但不化简不能得分.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)(1)解:
∵false
∴false,由正弦定理知,false,∴false,
由余弦定理知,false,∵false,∴false.
(2)证明:选择条件①,
∵false是false的中线,∴false,∴false,
∴false,∴false,
当且仅当false时,等号成立,∴false,故false存在最大值,为8.
选择条件②,
∵false是false的角平分线,∴false,
∵false,∴false,
即false,∴false,即false,
∴false,
当且仅当false时,等号成立,故false存在最小值,为8.
18.(Ⅰ)证:由false,当false时,得false,
两式相减得:falsefalsefalse,
化简得false,即false,
又false,所以false,所以false是false为首项,false为公比的等比数列.
(Ⅱ)解:由(1)得false,所以false,
所以false
falsefalse.
因为false,
令false,因为false,所以false,
又false,false,false,所以当false时,false,当false时,false,故false.
19.(1)证明:设false的中点为false,连结false,false,
由题意得false,false,false,
∵在false中,false,false为false的中点,∴false,
∵在false中,false,false,false,∴false,∴false,
∵false,false,false平面false,∴false平面false,false平面false,
∴平面false平面false.
(2)解:由(1)知false平面false,∴false,false,false,
以false为原点,false,false,false所在直线分别为false,false,false轴,建立空间直角坐标系,
则false,false,false,false,false,false,
false,false,false,
设平面false的法向量false,则false,取false,得false,
设平面false的法向量false,则false,取false,得false,
设二面角false的平面角为false,由图可得平面false和平面false所成角为锐角,
则false.
∴二面角false的余弦值为false.
20.解:(Ⅰ)第false次由甲组答题,是第false次由甲组答题,第false次继续由甲组答题的事件与第false次由乙组答题,第false次由甲组答题的事件和,它们互斥,又各次答题相互独立,
答对的题数之和为3的倍数分别为false,false,false,false,false,false,false,其概率为false,
则答对的题数之和不是3的倍数的概率为false,
所以第false次由甲组答题,第false次继续由甲组答题的概率为false,
第false次由乙组答题,第false次由甲组答题的概率为false,
因此false,则false
因为第一次由甲组开始,则false,所以false是首项为false,公比为false的等比数列,
所以false,即false
(Ⅱ)由于第1次由甲组答题,则只要第2次、第3次、第4次这3次中再由甲组答题一次即可,
由(1)可知false,false,false,
所以所求概率false
false.
所以false.
21.解:(1)false,∴false,
①若false,false在false上单调递减,在false上单调递增;
②若false,令false,false,
当false时,false,false,false,
∴false在false上单调递减,在false上单调递增;
当false时,同理可得,false在false,false上单调递减,在false上单调递增;
当false时,false,false恒成立,即false恒成立,∴false在false上单调递减.
综上所述,当false时,false的递减区间为false,无增区间;
当false时,false的递减区间为false,false,递增区间为false;
当false时,false的递减区间为false,递增区间为false;
当false时,false的递减区间为false,递增区间为false;
(2)证明:∵函数false有两个极值点false,false,由(1)可知false,且false,false是方程false两个根,∴false,false,
∴false
false
false;
令false,则false恒成立,
∴false在false上单调递增,∴false,即false.
22.解:(1)因为双曲线false,可得false,false,false,
由双曲线的定义可得false,又因为false,可得false,false,
因为false,由false,可得false,则点false的横坐标为false,
所以,false,∵false,可得false,即点false,
过点false且与渐近线false平行的直线的方程为false,
联立双曲线的方程,解得点false,
直线false的方程为false,点false到直线false的距离为false,且false,
因此,四边形false的面积为false;
(2)四边形false的面积为定值false,理由如下:
设点false,双曲线false的渐近线方程为false,
则直线false的方程为false,
联立,解得,即点false,
直线false的方程为false,即false,
点false到直线false的距离为,
false,且false,
因此,false(定值).
高二年级数学试题
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
4.本卷共6页,满分150分,考试时间120分钟.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.
1.已知false,false均为集合false的子集,且false,false,则false
A.false B.false C.false D.false
2.已知复数false,则以下命题中为真命题的是
A.false的共轭复数为false B.false的虚部为false
C.false D.false在复平面内对应的点在第一象限
3.已知向量false,false,false,且false,false,则false
A.3 B.false C.false D.false
4.围棋起源于中国,据先秦典籍《世本》记载:“尧造围棋,丹朱善之”,至今已有四千多年历史,围棋不仅能抒发意境、陶冶情操、修身养性、生慧增智,而且还与天象易理、兵法策略、治国安邦等相关联,蕴含着中华文化的丰富内涵在某次国际围棋比赛中,甲、乙两人进入最后决赛比赛采取五局三胜制,即先胜三局的一方获得比赛冠军,比赛结束.假设每局比赛甲胜乙的概率都为false,且各局比赛的胜负互不影响,则在不超过4局的比赛中甲获得冠军的概率为
A.false B.false C.false D.false
5.已知数列false的前false项和为false,若false,false,false,false为等差数列,则false
A.false B.false C.false D.false
6.函数false,false的值域是
A.false B.false C.false D.false
7.数学中的数形结合也可以组成世间万物的绚丽画面,一些优美的曲线是数学形象美、对称美、和谐美的产物,曲线false为四叶玫瑰线,下列结论正确的有
(1)方程false,表示的曲线在第二和第四象限;
(2)曲线false上任一点到坐标原点false的距离都不超过2;
(3)曲线false构成的四叶玫瑰线面积大于false;
(4)曲线false上有5个整点(横、纵坐标均为整数的点);
A.(1)(2) B.(1)(2)(3) C.(1)(2)(4) D.(1)(3)(4)
8.若函数false与函数false有公切线,则实数false的取值范围是
A.false B.false C.false D.false
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”过去10日,甲、乙、丙、丁四地新增疑似病例数据信息如下:
甲地:中位数为2,极差为5;
乙地:总体平均数为2,众数为2;
丙地:总体平均数为1,总体方差大于0;
丁地:总体平均数为2,总体方差为3.
则甲、乙、丙、丁四地中,一定没有发生大规模群体感染的有
A.甲地 B.乙地 C.丙地 D.丁地
10.如图,已知函数false(其中false,false,false)的图象与false轴交于点false,false,与false轴交于点false,false,false,false,false.则下列说法正确的有
A.false的最小正周期为12 B.false
C.false的最大值为false D.false在区间false上单调递增
11.已知点false,圆false,点false在圆false上运动,给出下列命题,其中正确的有
A.false的取值范围是false
B.在false轴上存在定点false,使false为定值;
C.设线段false的中点为false,则点false到直线false的距离的取值范围是false;
D.过直线false上一点false引圆false的两条切线,切点分别为false,false,则false的取值范围是false
12.在边长为2的等边三角形false中,点false,false分别是边false,false上的点,满足false且false,将false沿直线false折到false的位置.在翻折过程中,下列结论不成立的是
A.在边false上存在点false,使得在翻折过程中,满足false平面false
B.存在false,使得在翻折过程中的某个位置,满足平面false平面false
C.若false,当二面角false为直二面角时,false
D.在翻折过程中,四棱锥false体积的最大值记为false,false的最大值为false
三、填空题:本题共4小题,每小题5分,共20分.
13.false,false是两条不同的直线,false垂直于平面false,则“false”是“false”的__________条件.
14.已知椭圆false的一个焦点与抛物线false的焦点重合,过点false且斜率为false的直线交椭圆false于false,false两点,若false是线段false的中点,则椭圆false的方程为____________.
15.早期的毕达哥拉斯学派学者注意到:用等边三角形或正方形为表面可构成四种规则的立体图形,即正四面体、正六面体、正八面体和正二十面体,它们的各个面和多面角都全等.如图,正二十面体是由20个等边三角形组成的正多面体,共有12个顶点,30条棱,20个面,是五个柏拉图多面体之一.如果把false按false计算,则该正二十面体的表面积与该正二十面体的外接球表面积之比等于_____________.
16.某校学生在研究民间剪纸艺术时,发现剪纸时经常会沿纸的某条对称轴把纸对折.规格为false的长方形纸,对折1次共可以得到false,false两种规格的图形,它们的面积之和false,对折2次共可以得到false,false,false三种规格的图形,它们的面积之和false,以此类推.则对折4次共可以得到不同规格图形的种数为______________;如果对折false次,那么false____________false.(第1空2分,第2空3分)
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)已知false的内角false,false,false所对的边分别为false,false,false且满足false.
(1)求角false;
(2)设点false在边false上,且false,证明:若_____________,则false存在最大值或最小值.
请在下面的两个条件中选择一个条件填到上面的横线上,并证明.
①false是false的中线;
②false是false的角平分线.
18.(本小题满分12分)设数列false的前false项和为false,满足:false.
(1)求证:数列false为等比数列;
(2)求false,并求false的最大值.
19.(本小题满分12分)已知三棱锥false的展开图如图二,其中四边形false为边长等于false的正方形,false和false均为正三角形,在三棱锥false中:
(1)证明:平面false平面false;
(2)若false是false的中点,求二面角false的余弦值.
20.(本小题满分12分)当前,全国上下正处在新冠肺炎疫情“外防输入,内防反弹”的关键时期,为深入贯彻落实习近平总书记关于疫情防控的重要指示要求,始终把师生生命安全和身体健康放在第一位.结合全国第32个爱国卫生月要求,学校某班组织开展了“战疫有我,爱卫同行”防控疫情知识竞赛活动,抽取四位同学,分成甲、乙两组,每组两人,进行对战答题.规则如下:每次每位同学给出6道题目,其中有一道是送分题(即每位同学至少答对1题).若每次每组答对的题数之和为3的倍数,原答题组的人再继续答题;若答对的题数之和不是3的倍数,就由对方组接着答题.假设每位同学每次答题之间相互独立,第一次由甲组开始答题.求:
(1)若第false次由甲组答题的概率为false,求false;
(2)前4次答题中甲组恰好答题2次的概率为多少?
21.(本小题满分12分)已知函数false.
(1)讨论false的单调性;
(2)若false有2个极值点false,false,证明:false.
22.(本小题满分12分)如图,已知双曲线false的左、右焦点分别为false、false,若点false为双曲线false在第一象限上的一点,且满足false,过点false分别作双曲线false两条渐近线的平行线false、false与渐近线的交点分别是false和false.
(1)求四边形false的面积;
(2)若对于更一般的双曲线false,点false为双曲线false上任意一点,过点false分别作双曲线false两条渐近线的平行线false、false与渐近线的交点分别是false和false.请问四边形false的面积为定值吗?若是定值,求出该定值(用false、false表示该定值);若不是定值,请说明理由.
锡山高级中学2020~2021学年度第二学期期末检测
高二数学参考答案及评分标准
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
D
B
C
D
B
A
A
AD
ACD
BD
ABC
三、填空题:本题共4小题,每小题5分,共20分.
13.必要不充分条件 14.false 15.false 16.(1)5 (2)false
评分细则:13题严格按照答案,一点都不能变.写的潦草的不能得分
14题写成false也算对
15题不化简不得分
16题(1)2分,(2)3分.(2)中形式不唯一,但不化简不能得分.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)(1)解:
∵false
∴false,由正弦定理知,false,∴false,
由余弦定理知,false,∵false,∴false.
(2)证明:选择条件①,
∵false是false的中线,∴false,∴false,
∴false,∴false,
当且仅当false时,等号成立,∴false,故false存在最大值,为8.
选择条件②,
∵false是false的角平分线,∴false,
∵false,∴false,
即false,∴false,即false,
∴false,
当且仅当false时,等号成立,故false存在最小值,为8.
18.(Ⅰ)证:由false,当false时,得false,
两式相减得:falsefalsefalse,
化简得false,即false,
又false,所以false,所以false是false为首项,false为公比的等比数列.
(Ⅱ)解:由(1)得false,所以false,
所以false
falsefalse.
因为false,
令false,因为false,所以false,
又false,false,false,所以当false时,false,当false时,false,故false.
19.(1)证明:设false的中点为false,连结false,false,
由题意得false,false,false,
∵在false中,false,false为false的中点,∴false,
∵在false中,false,false,false,∴false,∴false,
∵false,false,false平面false,∴false平面false,false平面false,
∴平面false平面false.
(2)解:由(1)知false平面false,∴false,false,false,
以false为原点,false,false,false所在直线分别为false,false,false轴,建立空间直角坐标系,
则false,false,false,false,false,false,
false,false,false,
设平面false的法向量false,则false,取false,得false,
设平面false的法向量false,则false,取false,得false,
设二面角false的平面角为false,由图可得平面false和平面false所成角为锐角,
则false.
∴二面角false的余弦值为false.
20.解:(Ⅰ)第false次由甲组答题,是第false次由甲组答题,第false次继续由甲组答题的事件与第false次由乙组答题,第false次由甲组答题的事件和,它们互斥,又各次答题相互独立,
答对的题数之和为3的倍数分别为false,false,false,false,false,false,false,其概率为false,
则答对的题数之和不是3的倍数的概率为false,
所以第false次由甲组答题,第false次继续由甲组答题的概率为false,
第false次由乙组答题,第false次由甲组答题的概率为false,
因此false,则false
因为第一次由甲组开始,则false,所以false是首项为false,公比为false的等比数列,
所以false,即false
(Ⅱ)由于第1次由甲组答题,则只要第2次、第3次、第4次这3次中再由甲组答题一次即可,
由(1)可知false,false,false,
所以所求概率false
false.
所以false.
21.解:(1)false,∴false,
①若false,false在false上单调递减,在false上单调递增;
②若false,令false,false,
当false时,false,false,false,
∴false在false上单调递减,在false上单调递增;
当false时,同理可得,false在false,false上单调递减,在false上单调递增;
当false时,false,false恒成立,即false恒成立,∴false在false上单调递减.
综上所述,当false时,false的递减区间为false,无增区间;
当false时,false的递减区间为false,false,递增区间为false;
当false时,false的递减区间为false,递增区间为false;
当false时,false的递减区间为false,递增区间为false;
(2)证明:∵函数false有两个极值点false,false,由(1)可知false,且false,false是方程false两个根,∴false,false,
∴false
false
false;
令false,则false恒成立,
∴false在false上单调递增,∴false,即false.
22.解:(1)因为双曲线false,可得false,false,false,
由双曲线的定义可得false,又因为false,可得false,false,
因为false,由false,可得false,则点false的横坐标为false,
所以,false,∵false,可得false,即点false,
过点false且与渐近线false平行的直线的方程为false,
联立双曲线的方程,解得点false,
直线false的方程为false,点false到直线false的距离为false,且false,
因此,四边形false的面积为false;
(2)四边形false的面积为定值false,理由如下:
设点false,双曲线false的渐近线方程为false,
则直线false的方程为false,
联立,解得,即点false,
直线false的方程为false,即false,
点false到直线false的距离为,
false,且false,
因此,false(定值).
同课章节目录
