江苏省徐州市泉山区2020-2021学年高一下学期期末测试数学试题(一) Word版含解析
文档属性
| 名称 | 江苏省徐州市泉山区2020-2021学年高一下学期期末测试数学试题(一) Word版含解析 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-21 00:00:00 | ||
图片预览



文档简介
泉山区2020-2021学年高一下学期期末测试
数学试题
考试时间:120分钟 试卷满分:150分
注意事项:
1.答卷前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.空间两点false,false之间的距离等于( )
A.false B.false C.false D.false
2.在false中,已知false,false,false,则角false等于( )
A.30° B.120° C.60° D.150°
3.设α,β为不重合的平面,m,n为不重合的直线,则下列命题正确的是( )
A.若false,false,则false
B.若false,则false
C.若false,则false
D.若false,则false
4.已知圆false上有两个不同的点到直线false的距离等于false则false的取值范围是( )
A.false B.false
C.false D.false
5.对于非零向量false,下列命题正确的是( )
A.若false,则false
B.若false,则false
C.若false,则false
D.若false,则false的夹角为锐角
6.某中学有300名教师,其中初级教师60名,中级教师150名,高级教师90名.考虑采用分层抽样或系统抽样方法,从全校教师中抽取10人参加一个网络教学座谈会.采用分层抽样时,将初级教师随机编号为1~60,中级教师随机编号为61~210,高级教师随机编号为211~300;采用系统抽样时,将全校教师统一随机编号为1,2,…,300,并将整个编号从小到大依次均分为10组.
给出下列两组样本号码:①7,34,61,88,115,142,169,223,250,288;②26,32,90,100,138,172,188,211,254,297.
则下列结论中错误的是( )
A.样本①可能为分层抽样
B.样本②可能为分层抽样
C.样本①可能为系统抽样
D.样本②可能为系统抽样
7.已知false,且false,则false的值为( )
A.7 B.-7 C.false D.false
8.已知定义在false上的函数false满足false,且当false时,false.若对任意false,都有false成立,则false的取值范围是( )
A.false B.false C.false D.false
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下列判断正确的是( )
A.垂直于同一条直线的两条直线平行或异面;
B.与两条异面直线都相交的两条直线异面;
C.平行于两个相交平面的直线,平行于这两个平面的交线.
D.二面角的棱垂直于二面角平面角所在的平面
10.在三棱锥false中,下列说法正确的有( )
A.若false,则false在底面的射影为false外心
B.若false,则false在底面的射影为false的垂心
C.若false与底面所成的角相等,则false在底面的射影为false的重心
D.三个侧面false与底面所成二面角相等,则false在底面的射影为false的内心
11.已知等边false边长为false.点false在false边上,且false,false.下列结论中正确的是( )
A.false B.false C.false D.false
12.下列命题正确的是( )
A.若false,false,则false
B.若false,false,false,则false
C.若false,则false
D.若false,false,false,则false的最小值为3
三、填空题:本题共4小题,每小题5分,共20分.
13.已知函数false,false,给出下列四个结论:
①函数false的值域是false;②函数false为奇函数;③函数false的图象关于直线false对称;④若对任意false,都有false成立,则false的最小值为false.
其中正确结论的序号是___________.
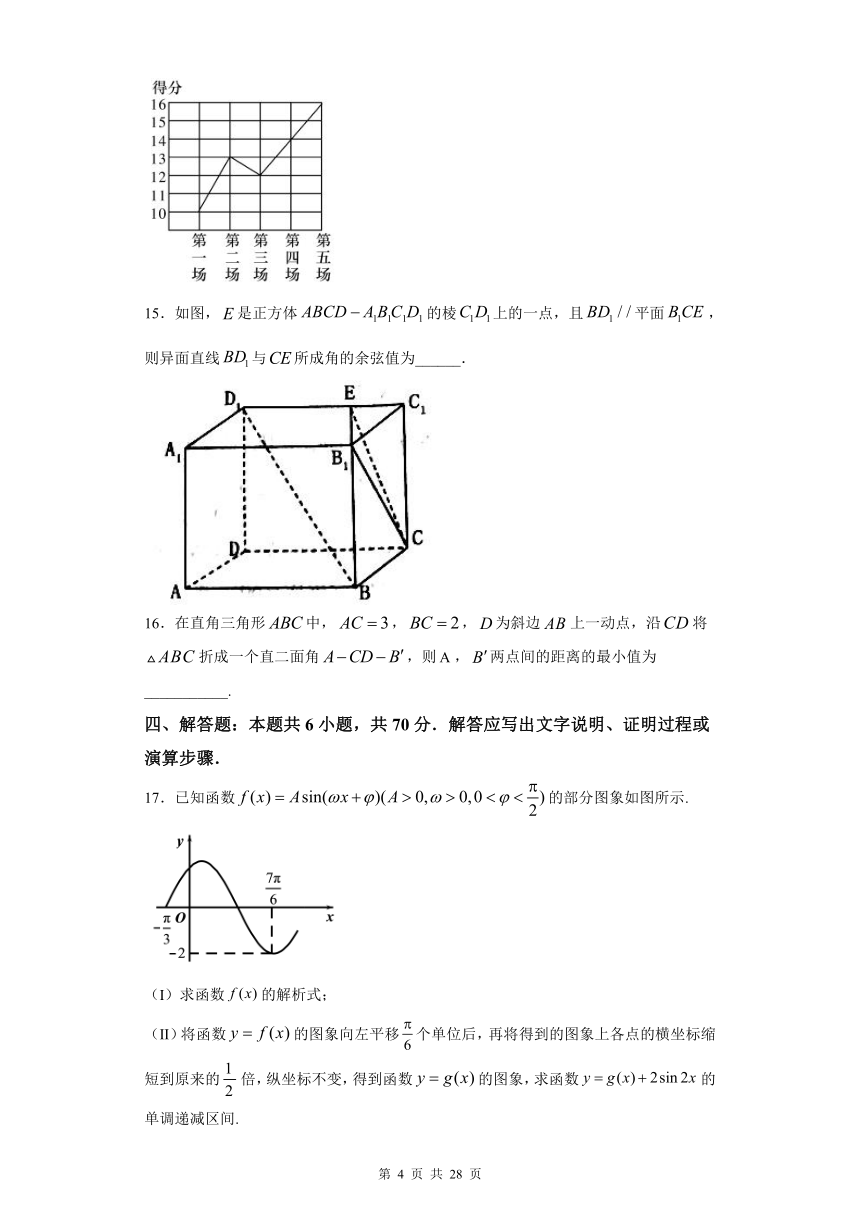
14.已知某篮球运动员在最近5场比赛中的得分的折线图如图所示,则该运动员得分的标准差为__________.
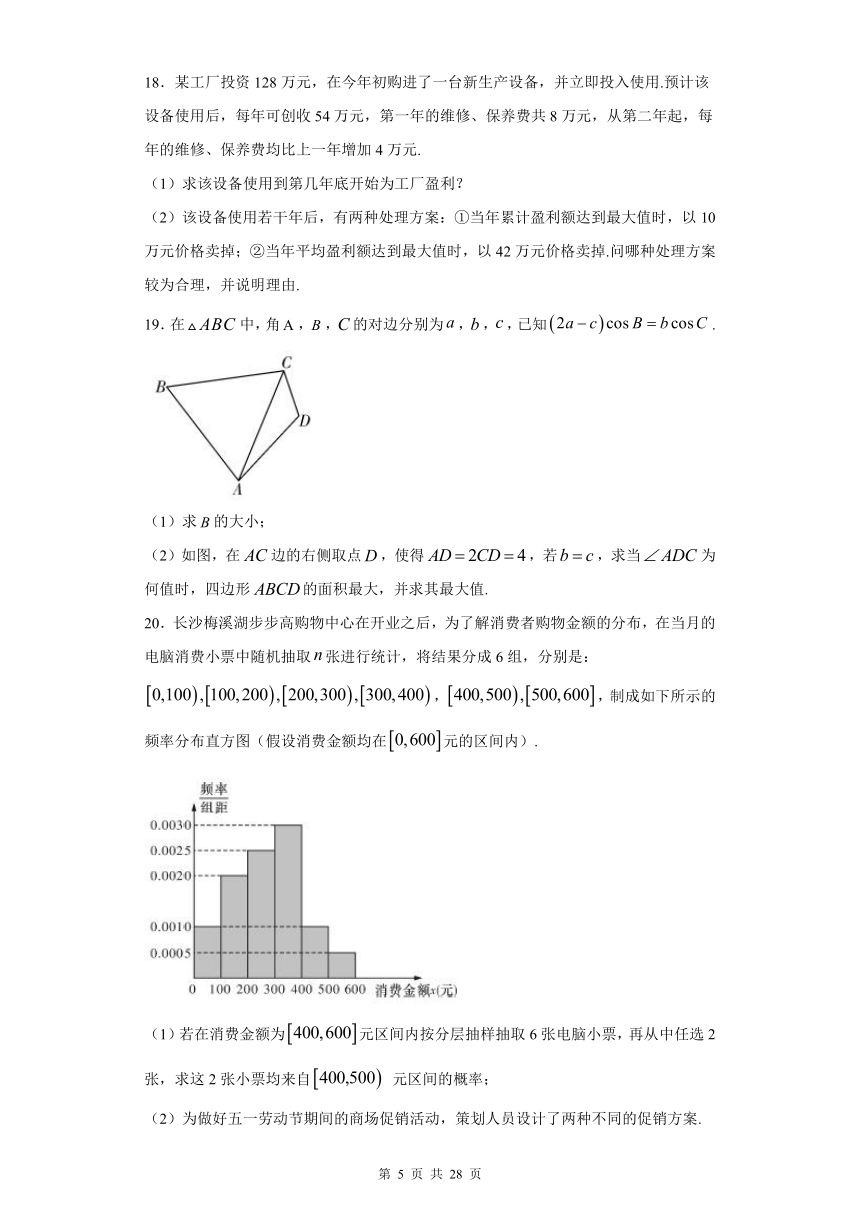
15.如图,false是正方体false的棱false上的一点,且false平面false,则异面直线false与false所成角的余弦值为______.
16.在直角三角形false中,false,false,false为斜边false上一动点,沿false将false折成一个直二面角false,则false,false两点间的距离的最小值为___________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知函数false的部分图象如图所示.
(Ⅰ)求函数false的解析式;
(Ⅱ)将函数false的图象向左平移false个单位后,再将得到的图象上各点的横坐标缩短到原来的false倍,纵坐标不变,得到函数false的图象,求函数false的单调递减区间.
18.某工厂投资128万元,在今年初购进了一台新生产设备,并立即投入使用.预计该设备使用后,每年可创收54万元,第一年的维修、保养费共8万元,从第二年起,每年的维修、保养费均比上一年增加4万元.
(1)求该设备使用到第几年底开始为工厂盈利?
(2)该设备使用若干年后,有两种处理方案:①当年累计盈利额达到最大值时,以10万元价格卖掉;②当年平均盈利额达到最大值时,以42万元价格卖掉.问哪种处理方案较为合理,并说明理由.
19.在false中,角false,false,false的对边分别为false,false,false,已知false.
(1)求false的大小;
(2)如图,在false边的右侧取点false,使得false,若false,求当false为何值时,四边形false的面积最大,并求其最大值.
20.长沙梅溪湖步步高购物中心在开业之后,为了解消费者购物金额的分布,在当月的电脑消费小票中随机抽取false张进行统计,将结果分成6组,分别是:false,false,制成如下所示的频率分布直方图(假设消费金额均在false元的区间内).
(1)若在消费金额为false元区间内按分层抽样抽取6张电脑小票,再从中任选2张,求这2张小票均来自false 元区间的概率;
(2)为做好五一劳动节期间的商场促销活动,策划人员设计了两种不同的促销方案.
方案一:全场商品打八折.
方案二:全场购物满100元减20元,满300元减80元,满500元减120元,以上减免只取最高优惠,不重复减免.利用直方图的信息分析:哪种方案优惠力度更大,并说明理由(直方图中每个小组取中间值作为该组数据的替代值).
21.已知函数false,false.
(1)当false时,求不等式false的解集;
(2)若存在false使关于false的方程false有四个不同的实根,求实数false的取值范围.
22.在三角形false中,false是线段false上一点,且false为线段false上一点.
(1)已知false,设false,求false;
(2)若E为线段false的中点,直线false与false相交于点F,求false.
泉山区2020-2021学年高一下学期期末测试
数学试题 解析版
考试时间:120分钟 试卷满分:150分
注意事项:
1.答卷前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.空间两点false,false之间的距离等于( )
A.false B.false C.false D.false
【答案】B
【分析】
利用空间中两点间距离公式即可求解.
【详解】
因为false,false,
所以false,
故选:B
2.在false中,已知false,false,false,则角false等于( )
A.30° B.120° C.60° D.150°
【答案】B
【分析】
利用余弦定理列出关系式,将false及false代入求出false的值,再利用余弦定理表示出false,将三边长代入求出false的值,即可确定出false的度数.
【详解】
false,
∴由余弦定理得: false,即false,
false,
∵false为三角形内角,
false.
故选:false.
【点睛】
本题考查余弦定理在解三角形中的应用,难度较易.
3.设α,β为不重合的平面,m,n为不重合的直线,则下列命题正确的是( )
A.若false,false,则false
B.若false,则false
C.若false,则false
D.若false,则false
【答案】D
【详解】
对于A,false,false时,若false ,则false,但题目中无条件false ,故A也不一定成立;
对于B,false,false.显然false不成立;
对于C,由面面平行的判定,一个面经过另一个面的垂线,仅有false 不能得到false 或false,故不正确.
对于D,false ,则false,又false,则false,结论成立;
故选D
4.已知圆false上有两个不同的点到直线false的距离等于false则false的取值范围是( )
A.false B.false
C.false D.false
【答案】C
【分析】
由圆false可得圆心和半径,画图,可得false,进而可得结果.
【详解】
由圆false
false过定点false
false,false上有两个不同点到false距离为false
即false,false
false的取值范围为false
故选:C.
【点睛】
关键点点睛:解决平面解析几何问题,画图分析,数形结合很关键.本题考查了运算求解能力和数形结合思想,属于一般题目.
5.对于非零向量false,下列命题正确的是( )
A.若false,则false
B.若false,则false
C.若false,则false
D.若false,则false的夹角为锐角
【答案】C
【分析】
选项A:两边不能同时除以false,应该移项,逆用向量数量积的运算律,得出结论;
选项B:根据公式false可以进行判断;
选项C:因为false是非零向量,所以false,可以依据这个进行判断;
选项D:两个数量积为负,可以得到两个向量的夹角为钝角或者是夹角,依此进行判断.
【详解】
解:A:若false,则false false,故A错误;
B:若false,则false,故B错误;
C:非零向量false,false,故C正确;
D:若false,则false的夹角为锐角或0,故D错误.
故选C.
【点睛】
本题考查了平面向量的线性运算以及数量积的运算问题,是基础题目.
6.某中学有300名教师,其中初级教师60名,中级教师150名,高级教师90名.考虑采用分层抽样或系统抽样方法,从全校教师中抽取10人参加一个网络教学座谈会.采用分层抽样时,将初级教师随机编号为1~60,中级教师随机编号为61~210,高级教师随机编号为211~300;采用系统抽样时,将全校教师统一随机编号为1,2,…,300,并将整个编号从小到大依次均分为10组.
给出下列两组样本号码:①7,34,61,88,115,142,169,223,250,288;②26,32,90,100,138,172,188,211,254,297.
则下列结论中错误的是( )
A.样本①可能为分层抽样
B.样本②可能为分层抽样
C.样本①可能为系统抽样
D.样本②可能为系统抽样
【答案】C
【分析】
利用分层抽样比求出初,中,高级教师抽取的人数,根据根据分层抽样、系统抽样的特征即可求解.
【详解】
若采用分层抽样,则抽样比例为false,
从而初,中,高级教师抽取的人数分别为2,5,3,
所以在编号1~60内抽取2个号码,在编号61~210内抽取5个号码,
在编号211~300内抽取3个号码,样本①,②都符合.
若采用系统抽样,则每30个编号抽取1个号码,
即在编号1~30,31~60,61~90,…,271~300内各抽取1个号码.
因为61,88都在编号61~90范围内,则样本①不符合,
但样本②符合,
故选:C.
7.已知false,且false,则false的值为( )
A.7 B.-7 C.false D.false
【答案】B
【分析】
根据正弦的二倍角公式可得false,再由同角三角函数的基本关系可得false,利用两角差的正切公式即可求解.
【详解】
因为false,则false.
又false,则false,
所以false,从而false,
所以false,
故选:B.
8.已知定义在false上的函数false满足false,且当false时,false.若对任意false,都有false成立,则false的取值范围是( )
A.false B.false C.false D.false
【答案】B
【分析】
利用基本不等式,结合false,分别求得false,false,false时函数的最小值分别为false, false,-1,得到m的最大值在区间false上,然后令 false,由false求解.
【详解】
当false时,false,
当且仅当false,即false时取等号.
当false时,false,则
falsefalse,
当且仅当false,即false时取等号,此时false成立.
当false时,false,则
falsefalse,
当且仅当false,即false时取等号.
令false,则false,false在false上单调递减,在false上单调递增.
令false,则false,解得false或false,即false或false,即false或false.
所以当false时,都有false成立,故false的取值范围是false,
故选:B.
【点睛】
关键点点睛:本题关键是求得false,false,false时函数的最小值,明确false时,m的最大值所在区间为false而得解.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下列判断正确的是( )
A.垂直于同一条直线的两条直线平行或异面;
B.与两条异面直线都相交的两条直线异面;
C.平行于两个相交平面的直线,平行于这两个平面的交线.
D.二面角的棱垂直于二面角平面角所在的平面
【答案】CD
【分析】
利用空间中直线与直线、直线与平面以及平面与平面之间的位置关系即可得出结果.
【详解】
A,垂直于同一条直线的两条直线平行或异面或相交,故A错误;
B,与两条异面直线都相交的两条直线异面或相交,故B错误;
C,由线面平行的性质可得,平行于两个相交平面的直线,
平行于这两个平面的交线,故C正确;
D,由二面角的平面角的定义可得,二面角的棱垂直于二面角平面角所在的平面,故D正确.
故选:CD
10.在三棱锥false中,下列说法正确的有( )
A.若false,则false在底面的射影为false外心
B.若false,则false在底面的射影为false的垂心
C.若false与底面所成的角相等,则false在底面的射影为false的重心
D.三个侧面false与底面所成二面角相等,则false在底面的射影为false的内心
【答案】ABD
【分析】
利用直角三角形全等,结合点的射影,外心定义可判定A正确,C错误;结合线面垂直的判定与性质及垂心定义可判定B;根据二面角的定义,线面垂直的判定与性质,内心的定义可以判定D正确.
【详解】
设S在底面所在平面内的射影为O,连接OA,OB,OC.
若SA=SB=SC,则RtSOA,SOB,SOC全等,所以OA=OB=OC,∴O为ABC的外心,故A正确;
若SA,SB,SC与底面所成的角相等,即∠SAO=∠SBO=∠SCO,则RtSOA,SOB,SOC全等,所以OA=OB=OC,∴O为ABC的外心,故C错误;
若SA⊥SB,SA⊥SC,SB⊥SC,则易知SA⊥平面SBC,故SA⊥BC,又∵SO⊥平面ABC,∴SO⊥BC,又∵SA∩SO=S,∴BC⊥平面SOA,∴BC⊥OA,同理AC⊥OB,BC⊥OA,∴O为ABC的垂心,故B正确;
三个侧面false与底面所成二面角相等,在底面内过O作BC,CA,AB的垂线,垂足分别为D,E,F,连接SD,SE,SF,
利用线面垂直的判定与性质易得SD⊥BC,SE⊥AC,SF⊥AB,故∠SDO,∠SEO,∠SFO为侧面与底面所成的二面角的平面角,故∠SDO=∠SEO=∠SFO,故SDO,SEO,SFO全等,故OE=OE=OF,又显然O在ABC外部时不合二面角相等的意义,故O为ABC的内心,故D正确.
故选:ABD.
【点睛】
本题考查三棱锥顶点在底面内的射影位置的判定,涉及线面角,二面角,线面垂直的判定与性质,三角形全等的判定与性质,属小综合题,难度一般.关键是熟练运用线面垂直的判定与性质,准确掌握线面角,二面角的概念.
11.已知等边false边长为false.点false在false边上,且false,false.下列结论中正确的是( )
A.false B.false C.false D.false
【答案】ABD
【分析】
作出图形,利用余弦定理计算出false,进而可求得false,并利用余弦定理求出false,false,可计算出false和false,进而可判断各选项的正误.
【详解】
如下图所示:
在false中,false,整理得false,
false,false,解得false,false,则false,
false,
由余弦定理得false,同理可得false,
所以,false,false,
因此,false,false.
故选:ABD.
【点睛】
本题考查解三角形,根据余弦定理解三角形是解答的关键,考查计算能力,属于中等题.
12.下列命题正确的是( )
A.若false,false,则false
B.若false,false,false,则false
C.若false,则false
D.若false,false,false,则false的最小值为3
【答案】ACD
【分析】
对选项A,利用不等式性质即可判断A正确;对选项B,利用特值法即可判断B错误;对选项C,利用基本不等式性质求解即可;对选项D,首先根据题意得到false,从而得到false,再展开利用基本不等式求解即可.
【详解】
对选项A,因为false,所以false,又因为false,所以false,故A正确;
对选项B,因为false,false,false,设false,false,false,
则false,false,false,故B错误;
对选项C,因为false,所以false
false,故C正确;
对选项D,因为false,所以false,
所以false,
当且仅当false,即false,false时,取等号.故D正确.
故选:ACD
三、填空题:本题共4小题,每小题5分,共20分.
13.已知函数false,false,给出下列四个结论:
①函数false的值域是false;②函数false为奇函数;③函数false的图象关于直线false对称;④若对任意false,都有false成立,则false的最小值为false.
其中正确结论的序号是___________.
【答案】①③④
【分析】
利用辅助角公式化简,结合正弦函数和余弦函数的性质,分别判断即可.
【详解】
false.①false的值域是false,结论正确;
②falsefalse为偶函数,结论错误;
③当false时,false,false取最大值,结论正确;
④因为false,false分别为false的最小值点和最大值点,则false,结论正确.
所以正确结论的序号是①③④.
故答案为:①③④
14.已知某篮球运动员在最近5场比赛中的得分的折线图如图所示,则该运动员得分的标准差为__________.
【答案】2
【分析】
由折线图写出每场比赛的分值并求false,由false求方差,进而可得标准差.
【详解】
由图知,该运动员5场比赛的得分分别为10,13,12,14,16,则平均数为false,
∴方差为false,所以标准差为2.
故答案为:2.
15.如图,false是正方体false的棱false上的一点,且false平面false,则异面直线false与false所成角的余弦值为______.
【答案】false
【详解】
不妨设正方体false的棱长为false,如图,当false为false中点时,false平面false,则false为直线false与false所成的角,在false中,
false,故答案为false.
【方法点晴】本题主要考查异面直线所成的角,属于难题.求异面直线所成的角主要方法有两种:一是向量法,根据几何体的特殊性质建立空间直角坐标系后,分别求出两直线的方向向量,再利用空间向量夹角的余弦公式求解;二是传统法,利用平行四边形、三角形中位线等方法找出两直线成的角,再利用平面几何性质求解.
16.在直角三角形false中,false,false,false为斜边false上一动点,沿false将false折成一个直二面角false,则false,false两点间的距离的最小值为___________.
【答案】false
【分析】
过点false作false于false,连结false,false,可证false,设false,利用余弦定理可求false,从而可求false,false两点间的距离的最小值.
【详解】
过点false作false于false,连结false,
由直二面角false可得平面false平面false,
而平面false平面false,false平面false,故false平面false,
而false平面false,故false.
设false,
则有false,false,false,
在false中,由余弦定理得
false,
在false中,由勾股定理得
false,
所以当false时,false取得最小值为false.
故答案为:false.
【点睛】
方法点睛:空间中最值的计算问题,往往转化为平面中几何对象的计算问题,注意利用余弦定理、正弦定理等来处理平面图形.
解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知函数false的部分图象如图所示.
(Ⅰ)求函数false的解析式;
(Ⅱ)将函数false的图象向左平移false个单位后,再将得到的图象上各点的横坐标缩短到原来的false倍,纵坐标不变,得到函数false的图象,求函数false的单调递减区间.
【答案】(Ⅰ)false(Ⅱ)false.
【分析】
(Ⅰ)直接利用函数的图象求出函数的关系式.(Ⅱ)利用(Ⅰ)的结论,进一步利用函数的图象的平移变化和伸缩变化的应用求出false,再利用正弦函数的单调性得单调区间即可
【详解】
(Ⅰ)由已知false图象得false
false,则false.
因为false,false
所以false.
因为false,false,
所以false.
所以false.
(Ⅱ)由题可得:false向左平移false得y=2cosx,横坐标再缩短到原来的false倍得false
故false
false
false.
因为false,false
所以false.
所以false的单调递减区间为false.
【点睛】
本题考查的知识要点:三角函数关系式的恒等变化,函数的图象的平移变化和伸缩变化的应用,函数单调性,主要考察学生的运算能力和转换能力,属于基础题型.
18.某工厂投资128万元,在今年初购进了一台新生产设备,并立即投入使用.预计该设备使用后,每年可创收54万元,第一年的维修、保养费共8万元,从第二年起,每年的维修、保养费均比上一年增加4万元.
(1)求该设备使用到第几年底开始为工厂盈利?
(2)该设备使用若干年后,有两种处理方案:①当年累计盈利额达到最大值时,以10万元价格卖掉;②当年平均盈利额达到最大值时,以42万元价格卖掉.问哪种处理方案较为合理,并说明理由.
【答案】(1)第4年;(2)选择方案②处理该设备较为合理,理由见解析.
【分析】
(1)设该设备第false年的维修,保养费为false万元,可得数列false是等差数列,利用等差数列的前false项和公式,结合一元二次不等式可得出该设备使用到开始为工厂盈利的年数;
(2)利用二次函数的性质可得方案①的总利润的最大值;利用基本不等式可得方案②总利润的最大值,进行比较可得答案.
【详解】
(1)设该设备第false年的维修,保养费为false万元,
据题意,数列false是首项为8,公差为4的等差数列,
所以前false年的维修、保养费之和false(万元).
设该设备使用false年后的累计盈利额为false万元,则false.
由false,得false,即false,解得false.
因为false,则false,所以该设备使用到第4年底开始为工厂盈利.
(2)①因为false,
则当false时,年累计盈利额达到最大值160万元.
所以按方案①处理,该设备的使用年限是12年,总利润为false(万元).
②因为falsefalse,则当false,
即false时,年平均盈利额达到最大值16万元.
所以按方案②处理,该设备的使用年限是8年,总利润为false(万元).
综上分析,两个方案的总利润相等,但方案①比方案②要多用4年时间才能获得170万元的总利润,
所以选择方案②处理该设备较为合理.
19.在false中,角false,false,false的对边分别为false,false,false,已知false.
(1)求false的大小;
(2)如图,在false边的右侧取点false,使得false,若false,求当false为何值时,四边形false的面积最大,并求其最大值.
【答案】(1)false;(2)当false时,四边形false的面积取得最大值false.
【分析】
(1)利用正弦定理把边转化为角,求出角B;
(2)设false,分别求出false的面积,利用三角函数求最值.
【详解】
(1)在false中,由正弦定理得false,
化简得false.
因为false,所以false.
又false,故false.
(2)由(1)知,false且false,所以false为等边三角形.
设false,则在false中,由余弦定理得false,
所以false,false,
四边形false的面积false.
因为false,所以false.当false,即false时,false.
所以当false时,四边形false的面积取得最大值false.
【点睛】
解三角形的基本策略:一是利用正弦定理实现“边化角”,二是利用余弦定理实现“角化边”;求最值也是一种常见类型,主要方法有两类,一是找到边之间的关系,利用基本不等式求最值,二是转化为关于某个角的函数,利用函数思想求最值.
20.长沙梅溪湖步步高购物中心在开业之后,为了解消费者购物金额的分布,在当月的电脑消费小票中随机抽取false张进行统计,将结果分成6组,分别是:false,false,制成如下所示的频率分布直方图(假设消费金额均在false元的区间内).
(1)若在消费金额为false元区间内按分层抽样抽取6张电脑小票,再从中任选2张,求这2张小票均来自false 元区间的概率;
(2)为做好五一劳动节期间的商场促销活动,策划人员设计了两种不同的促销方案.
方案一:全场商品打八折.
方案二:全场购物满100元减20元,满300元减80元,满500元减120元,以上减免只取最高优惠,不重复减免.利用直方图的信息分析:哪种方案优惠力度更大,并说明理由(直方图中每个小组取中间值作为该组数据的替代值).
【答案】(1)false(2)方案一的优惠力度更大.
【详解】
试题分析:(1)根据频率分布直方图,可知在false内抽6张,因此在false内抽4张,记为false,在false内抽2张,记为false,然后列举出从中任选2张所有的选法,在从中找到两张小票均来自false的的所有情况,即可求出概率.
(2)首先计算出各组频率,然后算出方案一购物的平均费用和方案二购物的平均费用,通过比较得到方案一的优惠力度更大.
试题解析:
(1)由直方图可知,按分层抽样在false内抽6张,
则false内抽4张,记为false,在false内抽2张,记为false,
设两张小票均来自false为事件false,
从中任选2张,有以下选法:false共15种.
其中,两张小票均来自false的有false,共6种,
∴false.
(2)解法一:由直方图可知,各组频率依次为0.1,0.2,0.25,0.3,0.1,0.05.
方案一购物的平均费用为:
false(元)
方案二购物的平均费用为:
false(元).
∴方案一的优惠力度更大.
(2)解法二:由直方图可知,各组频率依次为0.1,0.2,0.25,0.3,0.1,0.05,
方案一平均优惠金额为:
false(元).
方案二平均优惠金额为:false(元)
∴方案一的优惠力度更大.
21.已知函数false,false.
(1)当false时,求不等式false的解集;
(2)若存在false使关于false的方程false有四个不同的实根,求实数false的取值范围.
【答案】(1)答案见解析;(2)false.
【分析】
(1)先因式分解,对两根大小作讨论,求出解集;
(2)先令false,由false,则可得false,再将false有四个不同的实根,转化为false有两个不同正根,根据根与系数的关系,求出false的取值范围.
【详解】
(1)由题意,false,即false,
解方程false得false,false.
①当false时,即当false时,解不等式false,得false或false,
此时false的解集为false;
②当false时,即false时,解不等式false,得false,
此时false的解集为false;
③当false时,即当false时,解不等式false,得false或false,
此时false的解集为false;
综上,当false时,false的解集为false;
当false时,false的解集为false;
当false时,false的解集为false;
(2)当false时,令false,当且仅当false时,等号成立;
则关于false的方程false可化为false,
关于false的方程false有四个不等实根,
即false有两个不同正根,
则false,
由②③式可得false,
由①知:存在false使不等式false成立,
故false,
即false,解得false或false.
故实数false的取值范围是false.
【点睛】
已知函数有零点(方程有根)求参数值(取值范围)常用的方法:
(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解.
22.在三角形false中,false是线段false上一点,且false为线段false上一点.
(1)已知false,设false,求false;
(2)若E为线段false的中点,直线false与false相交于点F,求false.
【答案】(1)false;(2)false.
【分析】
(1)运用向量的线性运算得false,对比可求得false,可得答案;
(2)令false,由B、D、F三点共线,求得false,得出向量false的线性表示,再由向量数量积的运算可得答案.
【详解】
解:(1)false
false
false,
false
所以false;
(2)falsefalse,
令false,则false,
由B、D、F三点共线:false,
false,
falsefalse
false.
【点睛】
关键点点睛:解决向量的线性运算和数量积运算时,关键在于转化法的运用,将待求的向量转化为已知向量得以求解.
数学试题
考试时间:120分钟 试卷满分:150分
注意事项:
1.答卷前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.空间两点false,false之间的距离等于( )
A.false B.false C.false D.false
2.在false中,已知false,false,false,则角false等于( )
A.30° B.120° C.60° D.150°
3.设α,β为不重合的平面,m,n为不重合的直线,则下列命题正确的是( )
A.若false,false,则false
B.若false,则false
C.若false,则false
D.若false,则false
4.已知圆false上有两个不同的点到直线false的距离等于false则false的取值范围是( )
A.false B.false
C.false D.false
5.对于非零向量false,下列命题正确的是( )
A.若false,则false
B.若false,则false
C.若false,则false
D.若false,则false的夹角为锐角
6.某中学有300名教师,其中初级教师60名,中级教师150名,高级教师90名.考虑采用分层抽样或系统抽样方法,从全校教师中抽取10人参加一个网络教学座谈会.采用分层抽样时,将初级教师随机编号为1~60,中级教师随机编号为61~210,高级教师随机编号为211~300;采用系统抽样时,将全校教师统一随机编号为1,2,…,300,并将整个编号从小到大依次均分为10组.
给出下列两组样本号码:①7,34,61,88,115,142,169,223,250,288;②26,32,90,100,138,172,188,211,254,297.
则下列结论中错误的是( )
A.样本①可能为分层抽样
B.样本②可能为分层抽样
C.样本①可能为系统抽样
D.样本②可能为系统抽样
7.已知false,且false,则false的值为( )
A.7 B.-7 C.false D.false
8.已知定义在false上的函数false满足false,且当false时,false.若对任意false,都有false成立,则false的取值范围是( )
A.false B.false C.false D.false
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下列判断正确的是( )
A.垂直于同一条直线的两条直线平行或异面;
B.与两条异面直线都相交的两条直线异面;
C.平行于两个相交平面的直线,平行于这两个平面的交线.
D.二面角的棱垂直于二面角平面角所在的平面
10.在三棱锥false中,下列说法正确的有( )
A.若false,则false在底面的射影为false外心
B.若false,则false在底面的射影为false的垂心
C.若false与底面所成的角相等,则false在底面的射影为false的重心
D.三个侧面false与底面所成二面角相等,则false在底面的射影为false的内心
11.已知等边false边长为false.点false在false边上,且false,false.下列结论中正确的是( )
A.false B.false C.false D.false
12.下列命题正确的是( )
A.若false,false,则false
B.若false,false,false,则false
C.若false,则false
D.若false,false,false,则false的最小值为3
三、填空题:本题共4小题,每小题5分,共20分.
13.已知函数false,false,给出下列四个结论:
①函数false的值域是false;②函数false为奇函数;③函数false的图象关于直线false对称;④若对任意false,都有false成立,则false的最小值为false.
其中正确结论的序号是___________.
14.已知某篮球运动员在最近5场比赛中的得分的折线图如图所示,则该运动员得分的标准差为__________.
15.如图,false是正方体false的棱false上的一点,且false平面false,则异面直线false与false所成角的余弦值为______.
16.在直角三角形false中,false,false,false为斜边false上一动点,沿false将false折成一个直二面角false,则false,false两点间的距离的最小值为___________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知函数false的部分图象如图所示.
(Ⅰ)求函数false的解析式;
(Ⅱ)将函数false的图象向左平移false个单位后,再将得到的图象上各点的横坐标缩短到原来的false倍,纵坐标不变,得到函数false的图象,求函数false的单调递减区间.
18.某工厂投资128万元,在今年初购进了一台新生产设备,并立即投入使用.预计该设备使用后,每年可创收54万元,第一年的维修、保养费共8万元,从第二年起,每年的维修、保养费均比上一年增加4万元.
(1)求该设备使用到第几年底开始为工厂盈利?
(2)该设备使用若干年后,有两种处理方案:①当年累计盈利额达到最大值时,以10万元价格卖掉;②当年平均盈利额达到最大值时,以42万元价格卖掉.问哪种处理方案较为合理,并说明理由.
19.在false中,角false,false,false的对边分别为false,false,false,已知false.
(1)求false的大小;
(2)如图,在false边的右侧取点false,使得false,若false,求当false为何值时,四边形false的面积最大,并求其最大值.
20.长沙梅溪湖步步高购物中心在开业之后,为了解消费者购物金额的分布,在当月的电脑消费小票中随机抽取false张进行统计,将结果分成6组,分别是:false,false,制成如下所示的频率分布直方图(假设消费金额均在false元的区间内).
(1)若在消费金额为false元区间内按分层抽样抽取6张电脑小票,再从中任选2张,求这2张小票均来自false 元区间的概率;
(2)为做好五一劳动节期间的商场促销活动,策划人员设计了两种不同的促销方案.
方案一:全场商品打八折.
方案二:全场购物满100元减20元,满300元减80元,满500元减120元,以上减免只取最高优惠,不重复减免.利用直方图的信息分析:哪种方案优惠力度更大,并说明理由(直方图中每个小组取中间值作为该组数据的替代值).
21.已知函数false,false.
(1)当false时,求不等式false的解集;
(2)若存在false使关于false的方程false有四个不同的实根,求实数false的取值范围.
22.在三角形false中,false是线段false上一点,且false为线段false上一点.
(1)已知false,设false,求false;
(2)若E为线段false的中点,直线false与false相交于点F,求false.
泉山区2020-2021学年高一下学期期末测试
数学试题 解析版
考试时间:120分钟 试卷满分:150分
注意事项:
1.答卷前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.空间两点false,false之间的距离等于( )
A.false B.false C.false D.false
【答案】B
【分析】
利用空间中两点间距离公式即可求解.
【详解】
因为false,false,
所以false,
故选:B
2.在false中,已知false,false,false,则角false等于( )
A.30° B.120° C.60° D.150°
【答案】B
【分析】
利用余弦定理列出关系式,将false及false代入求出false的值,再利用余弦定理表示出false,将三边长代入求出false的值,即可确定出false的度数.
【详解】
false,
∴由余弦定理得: false,即false,
false,
∵false为三角形内角,
false.
故选:false.
【点睛】
本题考查余弦定理在解三角形中的应用,难度较易.
3.设α,β为不重合的平面,m,n为不重合的直线,则下列命题正确的是( )
A.若false,false,则false
B.若false,则false
C.若false,则false
D.若false,则false
【答案】D
【详解】
对于A,false,false时,若false ,则false,但题目中无条件false ,故A也不一定成立;
对于B,false,false.显然false不成立;
对于C,由面面平行的判定,一个面经过另一个面的垂线,仅有false 不能得到false 或false,故不正确.
对于D,false ,则false,又false,则false,结论成立;
故选D
4.已知圆false上有两个不同的点到直线false的距离等于false则false的取值范围是( )
A.false B.false
C.false D.false
【答案】C
【分析】
由圆false可得圆心和半径,画图,可得false,进而可得结果.
【详解】
由圆false
false过定点false
false,false上有两个不同点到false距离为false
即false,false
false的取值范围为false
故选:C.
【点睛】
关键点点睛:解决平面解析几何问题,画图分析,数形结合很关键.本题考查了运算求解能力和数形结合思想,属于一般题目.
5.对于非零向量false,下列命题正确的是( )
A.若false,则false
B.若false,则false
C.若false,则false
D.若false,则false的夹角为锐角
【答案】C
【分析】
选项A:两边不能同时除以false,应该移项,逆用向量数量积的运算律,得出结论;
选项B:根据公式false可以进行判断;
选项C:因为false是非零向量,所以false,可以依据这个进行判断;
选项D:两个数量积为负,可以得到两个向量的夹角为钝角或者是夹角,依此进行判断.
【详解】
解:A:若false,则false false,故A错误;
B:若false,则false,故B错误;
C:非零向量false,false,故C正确;
D:若false,则false的夹角为锐角或0,故D错误.
故选C.
【点睛】
本题考查了平面向量的线性运算以及数量积的运算问题,是基础题目.
6.某中学有300名教师,其中初级教师60名,中级教师150名,高级教师90名.考虑采用分层抽样或系统抽样方法,从全校教师中抽取10人参加一个网络教学座谈会.采用分层抽样时,将初级教师随机编号为1~60,中级教师随机编号为61~210,高级教师随机编号为211~300;采用系统抽样时,将全校教师统一随机编号为1,2,…,300,并将整个编号从小到大依次均分为10组.
给出下列两组样本号码:①7,34,61,88,115,142,169,223,250,288;②26,32,90,100,138,172,188,211,254,297.
则下列结论中错误的是( )
A.样本①可能为分层抽样
B.样本②可能为分层抽样
C.样本①可能为系统抽样
D.样本②可能为系统抽样
【答案】C
【分析】
利用分层抽样比求出初,中,高级教师抽取的人数,根据根据分层抽样、系统抽样的特征即可求解.
【详解】
若采用分层抽样,则抽样比例为false,
从而初,中,高级教师抽取的人数分别为2,5,3,
所以在编号1~60内抽取2个号码,在编号61~210内抽取5个号码,
在编号211~300内抽取3个号码,样本①,②都符合.
若采用系统抽样,则每30个编号抽取1个号码,
即在编号1~30,31~60,61~90,…,271~300内各抽取1个号码.
因为61,88都在编号61~90范围内,则样本①不符合,
但样本②符合,
故选:C.
7.已知false,且false,则false的值为( )
A.7 B.-7 C.false D.false
【答案】B
【分析】
根据正弦的二倍角公式可得false,再由同角三角函数的基本关系可得false,利用两角差的正切公式即可求解.
【详解】
因为false,则false.
又false,则false,
所以false,从而false,
所以false,
故选:B.
8.已知定义在false上的函数false满足false,且当false时,false.若对任意false,都有false成立,则false的取值范围是( )
A.false B.false C.false D.false
【答案】B
【分析】
利用基本不等式,结合false,分别求得false,false,false时函数的最小值分别为false, false,-1,得到m的最大值在区间false上,然后令 false,由false求解.
【详解】
当false时,false,
当且仅当false,即false时取等号.
当false时,false,则
falsefalse,
当且仅当false,即false时取等号,此时false成立.
当false时,false,则
falsefalse,
当且仅当false,即false时取等号.
令false,则false,false在false上单调递减,在false上单调递增.
令false,则false,解得false或false,即false或false,即false或false.
所以当false时,都有false成立,故false的取值范围是false,
故选:B.
【点睛】
关键点点睛:本题关键是求得false,false,false时函数的最小值,明确false时,m的最大值所在区间为false而得解.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下列判断正确的是( )
A.垂直于同一条直线的两条直线平行或异面;
B.与两条异面直线都相交的两条直线异面;
C.平行于两个相交平面的直线,平行于这两个平面的交线.
D.二面角的棱垂直于二面角平面角所在的平面
【答案】CD
【分析】
利用空间中直线与直线、直线与平面以及平面与平面之间的位置关系即可得出结果.
【详解】
A,垂直于同一条直线的两条直线平行或异面或相交,故A错误;
B,与两条异面直线都相交的两条直线异面或相交,故B错误;
C,由线面平行的性质可得,平行于两个相交平面的直线,
平行于这两个平面的交线,故C正确;
D,由二面角的平面角的定义可得,二面角的棱垂直于二面角平面角所在的平面,故D正确.
故选:CD
10.在三棱锥false中,下列说法正确的有( )
A.若false,则false在底面的射影为false外心
B.若false,则false在底面的射影为false的垂心
C.若false与底面所成的角相等,则false在底面的射影为false的重心
D.三个侧面false与底面所成二面角相等,则false在底面的射影为false的内心
【答案】ABD
【分析】
利用直角三角形全等,结合点的射影,外心定义可判定A正确,C错误;结合线面垂直的判定与性质及垂心定义可判定B;根据二面角的定义,线面垂直的判定与性质,内心的定义可以判定D正确.
【详解】
设S在底面所在平面内的射影为O,连接OA,OB,OC.
若SA=SB=SC,则RtSOA,SOB,SOC全等,所以OA=OB=OC,∴O为ABC的外心,故A正确;
若SA,SB,SC与底面所成的角相等,即∠SAO=∠SBO=∠SCO,则RtSOA,SOB,SOC全等,所以OA=OB=OC,∴O为ABC的外心,故C错误;
若SA⊥SB,SA⊥SC,SB⊥SC,则易知SA⊥平面SBC,故SA⊥BC,又∵SO⊥平面ABC,∴SO⊥BC,又∵SA∩SO=S,∴BC⊥平面SOA,∴BC⊥OA,同理AC⊥OB,BC⊥OA,∴O为ABC的垂心,故B正确;
三个侧面false与底面所成二面角相等,在底面内过O作BC,CA,AB的垂线,垂足分别为D,E,F,连接SD,SE,SF,
利用线面垂直的判定与性质易得SD⊥BC,SE⊥AC,SF⊥AB,故∠SDO,∠SEO,∠SFO为侧面与底面所成的二面角的平面角,故∠SDO=∠SEO=∠SFO,故SDO,SEO,SFO全等,故OE=OE=OF,又显然O在ABC外部时不合二面角相等的意义,故O为ABC的内心,故D正确.
故选:ABD.
【点睛】
本题考查三棱锥顶点在底面内的射影位置的判定,涉及线面角,二面角,线面垂直的判定与性质,三角形全等的判定与性质,属小综合题,难度一般.关键是熟练运用线面垂直的判定与性质,准确掌握线面角,二面角的概念.
11.已知等边false边长为false.点false在false边上,且false,false.下列结论中正确的是( )
A.false B.false C.false D.false
【答案】ABD
【分析】
作出图形,利用余弦定理计算出false,进而可求得false,并利用余弦定理求出false,false,可计算出false和false,进而可判断各选项的正误.
【详解】
如下图所示:
在false中,false,整理得false,
false,false,解得false,false,则false,
false,
由余弦定理得false,同理可得false,
所以,false,false,
因此,false,false.
故选:ABD.
【点睛】
本题考查解三角形,根据余弦定理解三角形是解答的关键,考查计算能力,属于中等题.
12.下列命题正确的是( )
A.若false,false,则false
B.若false,false,false,则false
C.若false,则false
D.若false,false,false,则false的最小值为3
【答案】ACD
【分析】
对选项A,利用不等式性质即可判断A正确;对选项B,利用特值法即可判断B错误;对选项C,利用基本不等式性质求解即可;对选项D,首先根据题意得到false,从而得到false,再展开利用基本不等式求解即可.
【详解】
对选项A,因为false,所以false,又因为false,所以false,故A正确;
对选项B,因为false,false,false,设false,false,false,
则false,false,false,故B错误;
对选项C,因为false,所以false
false,故C正确;
对选项D,因为false,所以false,
所以false,
当且仅当false,即false,false时,取等号.故D正确.
故选:ACD
三、填空题:本题共4小题,每小题5分,共20分.
13.已知函数false,false,给出下列四个结论:
①函数false的值域是false;②函数false为奇函数;③函数false的图象关于直线false对称;④若对任意false,都有false成立,则false的最小值为false.
其中正确结论的序号是___________.
【答案】①③④
【分析】
利用辅助角公式化简,结合正弦函数和余弦函数的性质,分别判断即可.
【详解】
false.①false的值域是false,结论正确;
②falsefalse为偶函数,结论错误;
③当false时,false,false取最大值,结论正确;
④因为false,false分别为false的最小值点和最大值点,则false,结论正确.
所以正确结论的序号是①③④.
故答案为:①③④
14.已知某篮球运动员在最近5场比赛中的得分的折线图如图所示,则该运动员得分的标准差为__________.
【答案】2
【分析】
由折线图写出每场比赛的分值并求false,由false求方差,进而可得标准差.
【详解】
由图知,该运动员5场比赛的得分分别为10,13,12,14,16,则平均数为false,
∴方差为false,所以标准差为2.
故答案为:2.
15.如图,false是正方体false的棱false上的一点,且false平面false,则异面直线false与false所成角的余弦值为______.
【答案】false
【详解】
不妨设正方体false的棱长为false,如图,当false为false中点时,false平面false,则false为直线false与false所成的角,在false中,
false,故答案为false.
【方法点晴】本题主要考查异面直线所成的角,属于难题.求异面直线所成的角主要方法有两种:一是向量法,根据几何体的特殊性质建立空间直角坐标系后,分别求出两直线的方向向量,再利用空间向量夹角的余弦公式求解;二是传统法,利用平行四边形、三角形中位线等方法找出两直线成的角,再利用平面几何性质求解.
16.在直角三角形false中,false,false,false为斜边false上一动点,沿false将false折成一个直二面角false,则false,false两点间的距离的最小值为___________.
【答案】false
【分析】
过点false作false于false,连结false,false,可证false,设false,利用余弦定理可求false,从而可求false,false两点间的距离的最小值.
【详解】
过点false作false于false,连结false,
由直二面角false可得平面false平面false,
而平面false平面false,false平面false,故false平面false,
而false平面false,故false.
设false,
则有false,false,false,
在false中,由余弦定理得
false,
在false中,由勾股定理得
false,
所以当false时,false取得最小值为false.
故答案为:false.
【点睛】
方法点睛:空间中最值的计算问题,往往转化为平面中几何对象的计算问题,注意利用余弦定理、正弦定理等来处理平面图形.
解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知函数false的部分图象如图所示.
(Ⅰ)求函数false的解析式;
(Ⅱ)将函数false的图象向左平移false个单位后,再将得到的图象上各点的横坐标缩短到原来的false倍,纵坐标不变,得到函数false的图象,求函数false的单调递减区间.
【答案】(Ⅰ)false(Ⅱ)false.
【分析】
(Ⅰ)直接利用函数的图象求出函数的关系式.(Ⅱ)利用(Ⅰ)的结论,进一步利用函数的图象的平移变化和伸缩变化的应用求出false,再利用正弦函数的单调性得单调区间即可
【详解】
(Ⅰ)由已知false图象得false
false,则false.
因为false,false
所以false.
因为false,false,
所以false.
所以false.
(Ⅱ)由题可得:false向左平移false得y=2cosx,横坐标再缩短到原来的false倍得false
故false
false
false.
因为false,false
所以false.
所以false的单调递减区间为false.
【点睛】
本题考查的知识要点:三角函数关系式的恒等变化,函数的图象的平移变化和伸缩变化的应用,函数单调性,主要考察学生的运算能力和转换能力,属于基础题型.
18.某工厂投资128万元,在今年初购进了一台新生产设备,并立即投入使用.预计该设备使用后,每年可创收54万元,第一年的维修、保养费共8万元,从第二年起,每年的维修、保养费均比上一年增加4万元.
(1)求该设备使用到第几年底开始为工厂盈利?
(2)该设备使用若干年后,有两种处理方案:①当年累计盈利额达到最大值时,以10万元价格卖掉;②当年平均盈利额达到最大值时,以42万元价格卖掉.问哪种处理方案较为合理,并说明理由.
【答案】(1)第4年;(2)选择方案②处理该设备较为合理,理由见解析.
【分析】
(1)设该设备第false年的维修,保养费为false万元,可得数列false是等差数列,利用等差数列的前false项和公式,结合一元二次不等式可得出该设备使用到开始为工厂盈利的年数;
(2)利用二次函数的性质可得方案①的总利润的最大值;利用基本不等式可得方案②总利润的最大值,进行比较可得答案.
【详解】
(1)设该设备第false年的维修,保养费为false万元,
据题意,数列false是首项为8,公差为4的等差数列,
所以前false年的维修、保养费之和false(万元).
设该设备使用false年后的累计盈利额为false万元,则false.
由false,得false,即false,解得false.
因为false,则false,所以该设备使用到第4年底开始为工厂盈利.
(2)①因为false,
则当false时,年累计盈利额达到最大值160万元.
所以按方案①处理,该设备的使用年限是12年,总利润为false(万元).
②因为falsefalse,则当false,
即false时,年平均盈利额达到最大值16万元.
所以按方案②处理,该设备的使用年限是8年,总利润为false(万元).
综上分析,两个方案的总利润相等,但方案①比方案②要多用4年时间才能获得170万元的总利润,
所以选择方案②处理该设备较为合理.
19.在false中,角false,false,false的对边分别为false,false,false,已知false.
(1)求false的大小;
(2)如图,在false边的右侧取点false,使得false,若false,求当false为何值时,四边形false的面积最大,并求其最大值.
【答案】(1)false;(2)当false时,四边形false的面积取得最大值false.
【分析】
(1)利用正弦定理把边转化为角,求出角B;
(2)设false,分别求出false的面积,利用三角函数求最值.
【详解】
(1)在false中,由正弦定理得false,
化简得false.
因为false,所以false.
又false,故false.
(2)由(1)知,false且false,所以false为等边三角形.
设false,则在false中,由余弦定理得false,
所以false,false,
四边形false的面积false.
因为false,所以false.当false,即false时,false.
所以当false时,四边形false的面积取得最大值false.
【点睛】
解三角形的基本策略:一是利用正弦定理实现“边化角”,二是利用余弦定理实现“角化边”;求最值也是一种常见类型,主要方法有两类,一是找到边之间的关系,利用基本不等式求最值,二是转化为关于某个角的函数,利用函数思想求最值.
20.长沙梅溪湖步步高购物中心在开业之后,为了解消费者购物金额的分布,在当月的电脑消费小票中随机抽取false张进行统计,将结果分成6组,分别是:false,false,制成如下所示的频率分布直方图(假设消费金额均在false元的区间内).
(1)若在消费金额为false元区间内按分层抽样抽取6张电脑小票,再从中任选2张,求这2张小票均来自false 元区间的概率;
(2)为做好五一劳动节期间的商场促销活动,策划人员设计了两种不同的促销方案.
方案一:全场商品打八折.
方案二:全场购物满100元减20元,满300元减80元,满500元减120元,以上减免只取最高优惠,不重复减免.利用直方图的信息分析:哪种方案优惠力度更大,并说明理由(直方图中每个小组取中间值作为该组数据的替代值).
【答案】(1)false(2)方案一的优惠力度更大.
【详解】
试题分析:(1)根据频率分布直方图,可知在false内抽6张,因此在false内抽4张,记为false,在false内抽2张,记为false,然后列举出从中任选2张所有的选法,在从中找到两张小票均来自false的的所有情况,即可求出概率.
(2)首先计算出各组频率,然后算出方案一购物的平均费用和方案二购物的平均费用,通过比较得到方案一的优惠力度更大.
试题解析:
(1)由直方图可知,按分层抽样在false内抽6张,
则false内抽4张,记为false,在false内抽2张,记为false,
设两张小票均来自false为事件false,
从中任选2张,有以下选法:false共15种.
其中,两张小票均来自false的有false,共6种,
∴false.
(2)解法一:由直方图可知,各组频率依次为0.1,0.2,0.25,0.3,0.1,0.05.
方案一购物的平均费用为:
false(元)
方案二购物的平均费用为:
false(元).
∴方案一的优惠力度更大.
(2)解法二:由直方图可知,各组频率依次为0.1,0.2,0.25,0.3,0.1,0.05,
方案一平均优惠金额为:
false(元).
方案二平均优惠金额为:false(元)
∴方案一的优惠力度更大.
21.已知函数false,false.
(1)当false时,求不等式false的解集;
(2)若存在false使关于false的方程false有四个不同的实根,求实数false的取值范围.
【答案】(1)答案见解析;(2)false.
【分析】
(1)先因式分解,对两根大小作讨论,求出解集;
(2)先令false,由false,则可得false,再将false有四个不同的实根,转化为false有两个不同正根,根据根与系数的关系,求出false的取值范围.
【详解】
(1)由题意,false,即false,
解方程false得false,false.
①当false时,即当false时,解不等式false,得false或false,
此时false的解集为false;
②当false时,即false时,解不等式false,得false,
此时false的解集为false;
③当false时,即当false时,解不等式false,得false或false,
此时false的解集为false;
综上,当false时,false的解集为false;
当false时,false的解集为false;
当false时,false的解集为false;
(2)当false时,令false,当且仅当false时,等号成立;
则关于false的方程false可化为false,
关于false的方程false有四个不等实根,
即false有两个不同正根,
则false,
由②③式可得false,
由①知:存在false使不等式false成立,
故false,
即false,解得false或false.
故实数false的取值范围是false.
【点睛】
已知函数有零点(方程有根)求参数值(取值范围)常用的方法:
(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解.
22.在三角形false中,false是线段false上一点,且false为线段false上一点.
(1)已知false,设false,求false;
(2)若E为线段false的中点,直线false与false相交于点F,求false.
【答案】(1)false;(2)false.
【分析】
(1)运用向量的线性运算得false,对比可求得false,可得答案;
(2)令false,由B、D、F三点共线,求得false,得出向量false的线性表示,再由向量数量积的运算可得答案.
【详解】
解:(1)false
false
false,
false
所以false;
(2)falsefalse,
令false,则false,
由B、D、F三点共线:false,
false,
falsefalse
false.
【点睛】
关键点点睛:解决向量的线性运算和数量积运算时,关键在于转化法的运用,将待求的向量转化为已知向量得以求解.
同课章节目录
