山东省济宁市曲阜市2020-2021学年八年级下学期期末复习数学试卷 (Word版含答案)
文档属性
| 名称 | 山东省济宁市曲阜市2020-2021学年八年级下学期期末复习数学试卷 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 147.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-21 09:16:07 | ||
图片预览



文档简介
2020-2021学年山济宁市曲阜市数学八(下)期末复习试卷
一.选择题(共12小题,满分36分,每小题3分)
1.(3分)式子中,x的取值范围是( )
A.x≤3 B.x≥3 C.x>3 D.x≥3且x≠4
2.(3分)下列式子为最简二次根式的是( )
A. B. C. D.
3.(3分)下列长度的三条线段能组成直角三角形的是( )
A.5,11,12 B.3,4,5 C.4,6,8 D.6,12,13
4.(3分)某中学为了让学生的跳远在中考体育测试中取得满意的成绩,在锻炼一个月后,学校对九年级一班的45名学生进行测试
跳远成绩(cm)
160
170
180
190
200
220
人数
3
9
6
9
15
3
这些运动员跳远成绩的中位数和众数分别是( )
A.190,200 B.9,9 C.15,9 D.185,200
5.(3分)下列命题中,正确的是( )
A.四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线相等的菱形是正方形
6.(3分)如图为正比例函数y=kx(k≠0)的图象,则一次函数y=x+k的大致图象是( )
A. B.
C. D.
7.(3分)下列方程一定是一元二次方程的是( )
A.3x2+﹣1=0 B.5x2﹣6y﹣3=0 C.ax2﹣x+2=0 D.3x2﹣2x﹣1=0
8.(3分)在四边形ABCD中,点E、F、G、H分别是AB、BC、CD、AD的中点,下列条件中能使四边形EFGH为矩形的是( )
A.AB⊥BC B.AB=BC C.AC⊥BD D.AC=BD
9.(3分)已知点A(a,)是两函数y=kx﹣2与图象的交点.则实数k等于( )
A. B. C. D.1
10.(3分)设x1,x2是一元二次方程x2﹣2x﹣3=0的两根,则x1+x2=( )
A.﹣2 B.2 C.3 D.﹣3
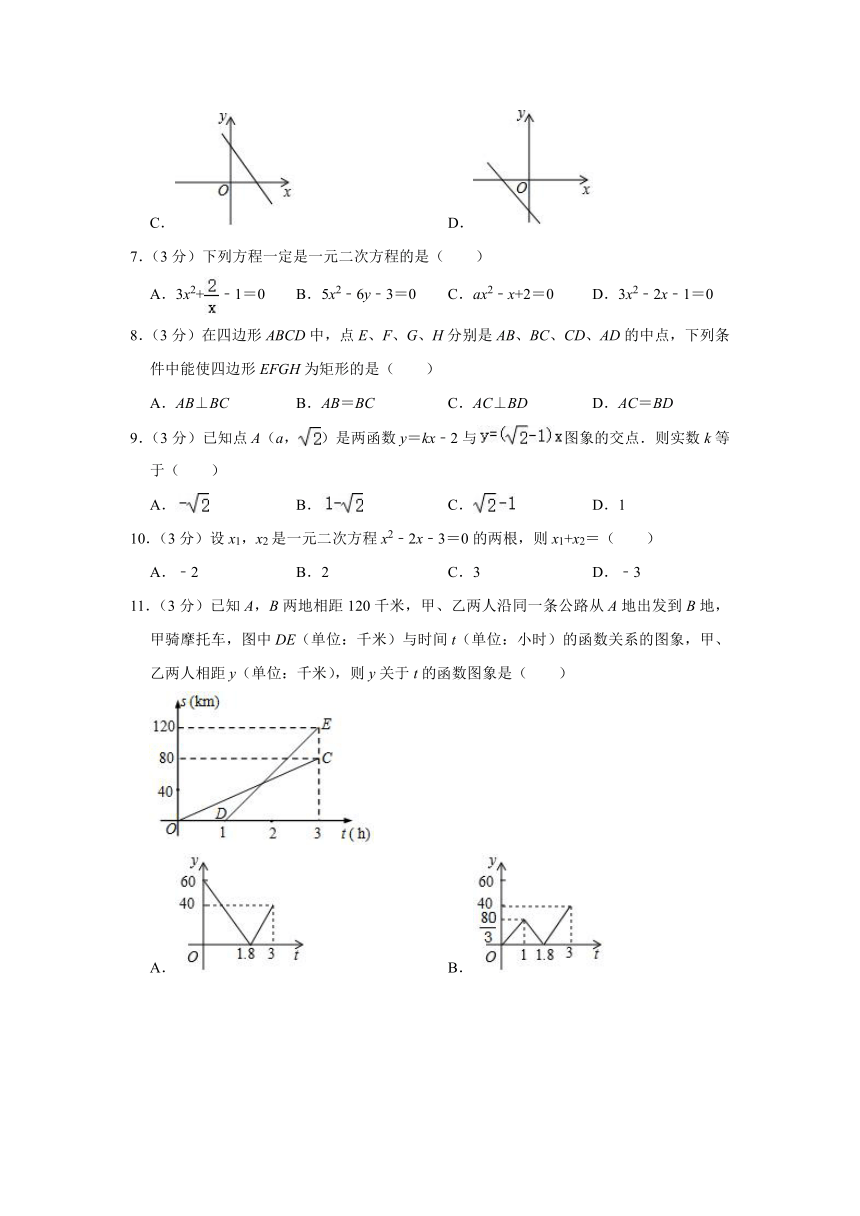
11.(3分)已知A,B两地相距120千米,甲、乙两人沿同一条公路从A地出发到B地,甲骑摩托车,图中DE(单位:千米)与时间t(单位:小时)的函数关系的图象,甲、乙两人相距y(单位:千米),则y关于t的函数图象是( )
A. B.
C. D.
12.(3分)如图,正方形ABCD中,AB=3,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G
①点G是BC的中点;
②FG=FC;
③AG∥CF;
④S△FGC=.
其中正确结论是( )
A.①② B.②④ C.①②③ D.①③④
二.填空题(共4小题,满分16分,每小题4分)
13.(4分)某校九年级甲、乙两个班的期末数学平均成绩都为89分,且甲班期末数学成绩的方差为S甲2=0.02(分2),乙班期末数学成绩的方差为S乙2=1.2(分2),则期末数学成绩 班更稳定.(填甲或乙)
14.(4分)一次函数y=(m﹣3)x﹣2的图象经过二、三、四象限,则m的取值范围是 .
15.(4分)已知:一元二次方程x2﹣6x+c=0有一个根为2,则另一根为 .
16.(4分)如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处cm,且tan∠EFC= .
三.解答题(共7小题,满分68分)
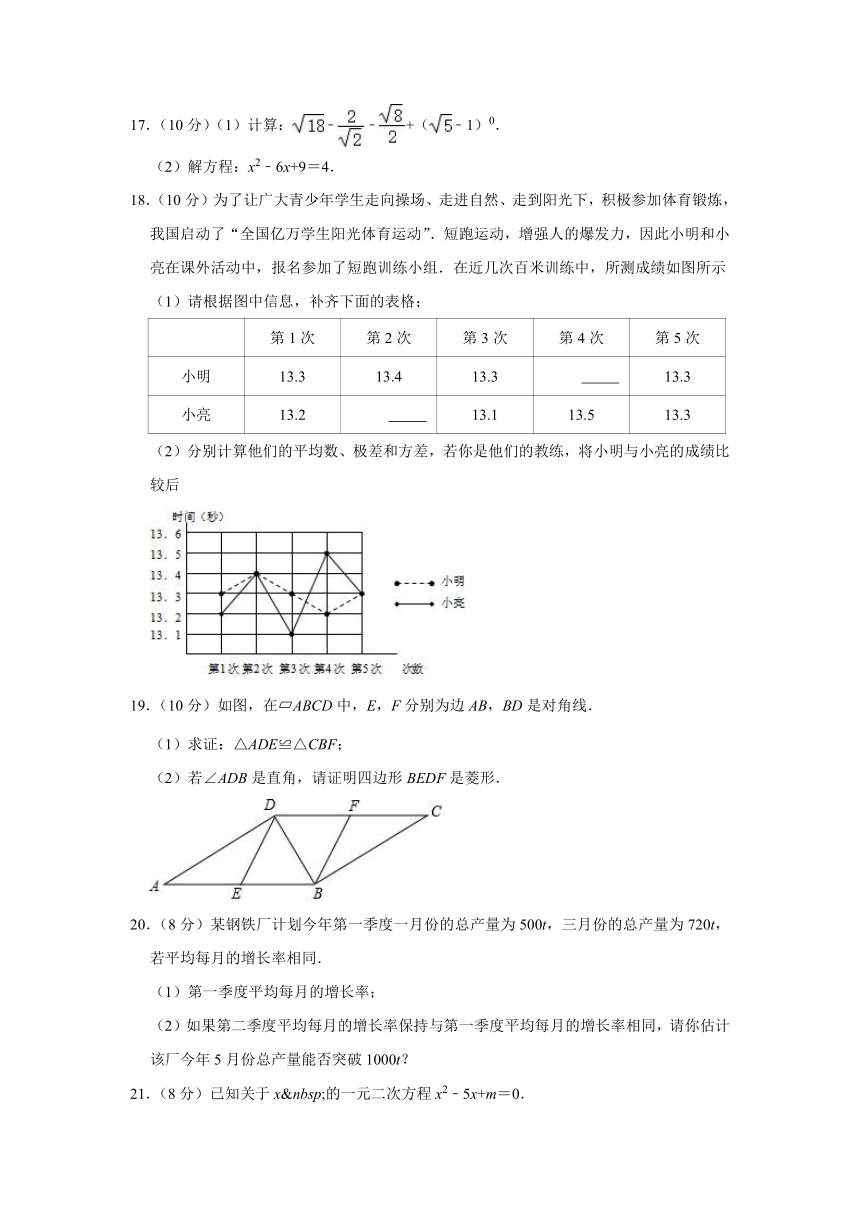
17.(10分)(1)计算:﹣﹣+(﹣1)0.
(2)解方程:x2﹣6x+9=4.
18.(10分)为了让广大青少年学生走向操场、走进自然、走到阳光下,积极参加体育锻炼,我国启动了“全国亿万学生阳光体育运动”.短跑运动,增强人的爆发力,因此小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示
(1)请根据图中信息,补齐下面的表格;
第1次
第2次
第3次
第4次
第5次
小明
13.3
13.4
13.3
13.3
小亮
13.2
13.1
13.5
13.3
(2)分别计算他们的平均数、极差和方差,若你是他们的教练,将小明与小亮的成绩比较后
19.(10分)如图,在?ABCD中,E,F分别为边AB,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,请证明四边形BEDF是菱形.
20.(8分)某钢铁厂计划今年第一季度一月份的总产量为500t,三月份的总产量为720t,若平均每月的增长率相同.
(1)第一季度平均每月的增长率;
(2)如果第二季度平均每月的增长率保持与第一季度平均每月的增长率相同,请你估计该厂今年5月份总产量能否突破1000t?
21.(8分)已知关于x 的一元二次方程x2﹣5x+m=0.
(1)若方程有实数根,求实数m 的取值范围;
(2)若方程两实数根为x1,x2,且满足3x1﹣2x2=5,求实数m 的值.
22.(10分)直线l经过(2,3)和(﹣2,﹣1)两点,它还与x轴交于A点,与经过原点的直线OB交于第三象限的B点,且∠ABO=30°.求:
(1)点A、C的坐标;
(2)点B的坐标.
23.(12分)某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)
x/元
…
15
20
25
…
y/件
…
25
20
15
…
已知日销售量y是销售价x的一次函数.
(1)求日销售量y(件)与每件产品的销售价x(元)之间的函数表达式;
(2)当每件产品的销售价定为35元时,此时每日的销售利润是多少元?
参考答案
一.选择题(共12小题,满分36分,每小题3分)
1.解:由题意得:,
解得:x≥3且x≠6.
故选:D.
2.解:A、=|a+b|,故本选项不符合题意;
B、=2,故本选项不符合题意;
C、是最简二次根式;
D、=,不是最简二次根式;
故选:C.
3.解:A、因为52+118≠122,所以三条线段不能组成直角三角形;
B、因为34+42=42,所以三条线段能组成直角三角形;
C、因为47+62≠42,所以三条线段不能组成直角三角形;
D、因为65+122≠132,所以三条线段不能组成直角三角形.
故选:B.
4.解:在这一组数据中200是出现次数最多的,
故众数是200cm;
在这45个数中,处于中间位置的第23个数是190.
所以这些学生跳远成绩的中位数和众数分别是190,200.
故选:A.
5.解:A,错误;
B,错误,但不是正方形;
C,错误;
D,正确;
故选:D.
6.解:因为正比例函数y=kx(k≠0)的图象经过第二、四象限,
所以k<0,
所以一次函数y=x+k的图象经过一、三、四象限,
故选:B.
7.解:A、是分式方程;
B、是二元二次方程;
C、a=0时,故C错误;
D、是一元二次方程;
故选:D.
8.证明:∵点E、F、G、H分别是边AB、CD,
∴EF=ACAC,
∴EF=GH,同理EH=FG
∴四边形EFGH是平行四边形;
当对角线AC、BD互相垂直时,
∴EF与FG垂直.
∴四边形EFGH是矩形.
故选:C.
9.解:∵A(a,)是两函数y=kx﹣2与,
∴A(a,)满足两函数的解析式y=kx﹣7与,
∴,
解得,.
故选:D.
10.解:根据根与系数的关系,
x1+x2=﹣=2.
故选:B.
11.解:由题意和图象可得,乙到达B地时甲距A地120km;
甲的速度是:120÷(3﹣1)=60km/h,乙的速度是:80÷4=;
设乙出发后被甲追上的时间为xh,则60(x﹣4)=x,即乙出发后被甲追上的时间为1.5h.
所以符合题意的函数图象只有选项B.
故选:B.
12.解:∵四边形ABCD是正方形,
∴AB=AD=DC=3,∠B=D=90°,
∵CD=3DE,
∴DE=8,
∵△ADE沿AE折叠得到△AFE,
∴DE=EF=1,AD=AF,
∴AF=AB,
在Rt△ABG和Rt△AFG中,
,
∴Rt△ABG≌Rt△AFG(HL),
∴BG=FG,∠AGB=∠AGF,
设BG=x,则CG=BC﹣BG=3﹣x,
在Rt△ECG中,由勾股定理得:CG2+CE2=EG2,
∵CG=3﹣x,CE=2,
∴(3﹣x)4+22=(x+4)2
解得:x=1.8,
∴BG=GF=CG=1.5,①正确;
∴∠CFG=∠FCG,
∵∠BGF=∠CFG+∠FCG,
又∵∠BGF=∠AGB+∠AGF,
∴∠CFG+∠FCG=∠AGB+∠AGF,
∵∠AGB=∠AGF,∠CFG=∠FCG,
∴∠AGB=∠FCG,
∴AG∥CF,③正确;
∵△CFG和△CEG中,分别把FG和GE看作底边,
则这两个三角形的高相同.
∴===,
∵S△GCE=×1.4×2=1.4,
∴S△CFG=×8.5=;
正确的结论是①③④,
故选:D.
二.填空题(共4小题,满分16分,每小题4分)
13.解:因为九年级甲、乙两个班的期末数学平均成绩都为89分甲2=0.02<S乙2=1.2,方差小的为甲,
所以期末数学成绩甲班更稳定.
故答案为:甲.
14.解:∵一次函数y=(m﹣3)x﹣2的图象经过二、三、四象限,
∴m﹣7<0,
∴m<3,
故答案为:m<3
15.解:设方程另一根为t,
根据题意得2+t=6,
解得t=5.
故答案为4.
16.解:设CE=3k,则CF=4k,
∴DC=AB=5k,
∵∠AFB+∠BAF=90°,∠AFB+∠EFC=90°,
∴∠BAF=∠EFC,
∴tan∠BAF=tan∠EFC=,
∴BF=7k,AF=BC=AD=10k,
在Rt△AFE中由勾股定理得AE===5,
解得:k=3,
故矩形ABCD的周长=2(AB+BC)=2(7k+10k)=36cm.
三.解答题(共7小题,满分68分)
17.解:(1)原式=3﹣﹣+1=;
(2)∵x2﹣6x+2=4,
∴(x﹣3)5=4,
则x﹣3=±5,
∴x1=5,x5=1.
18.解:(1)
第1次
第2次
第4次
第4次
第5次
小明
13.6
13.4
13.3
13.4
13.3
小亮
13.2
13.7
13.1
13.5
13.7
(2)小明:平均分为13.3,
极差为0.3,
方差为0.004,
小亮:平均分为13.3,
极差为8.4,
方差为0.02,
∵S7小明<S2小亮,
∴小明同学的成绩较为稳定,但是他的最高成绩没有小亮高,有待提高.
而小亮同学爆发力还行,但是成绩不稳定.
19.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,
∵E、F分别为边AB,
∴AE=ABCD,
∴AE=CF,
在△ADE和△CBF中,
∵,
∴△ADE≌△CBF(SAS).
(2)证明:∵E、F分别为边AB,
∴DF=DCAB,
又∵在?ABCD中,AB∥CD,
∴DF∥BE,DF=BE,
∴四边形DEBF为平行四边形,
∵DB⊥BC,
∴∠DBC=90°,
∴△DBC为直角三角形,
又∵F为边DC的中点,
∴BF=DC=DF,
又∵四边形DEBF为平行四边形,
∴四边形DEBF是菱形.
20.解:(1)设第一季度平均每月的增长率为x,
根据题意得:500(1+x)2=720,
解得:x5=0.2=20%,x5=﹣2.2(舍去).
答:第一季度平均每月的增长率为20%.
(2)720×(5+20%)2=1036.8(t),
∵1036.8>1000,
∴该厂今年5月份总产量能突破1000t.
21.解:(1)∵方程有实数根,
∴△=25﹣4m≥0,
解得,m≤;
(2)由一元二次方程根与系数的关系可知,x1+x2=2,x1?x2=m,
∵2x1﹣2x8=5,
∴3x5+3x2﹣3x2=5,
∴﹣5x2=﹣10,
解得,x2=8,
把x=2代入原方程得,m=6.
22.解:(1)设直线l的解析式为:y=kx+b,
则,
解得:,
∴直线l的解析式为:y=x+1,
则点A的坐标(﹣1,8),1).
(2)作OD⊥AC于D,BF⊥y轴于F,
∵OA=1,OC=2,
∴AC=,
则OD=AD=CD=,
在Rt△BOD中,∠ABO=30°,
BD=,则BC=,
|BF|=|CF|=?=,
|OF|=﹣1=,
∵B在第三象限,
∴点B的坐标为:(﹣,﹣).
23.解:(1)设日销售量y(件)与每件产品的销售价x(元)之间的函数表达式是y=kx+b,
,
解得,,
即日销售量y(件)与每件产品的销售价x(元)之间的函数表达式是y=﹣x+40;
(2)当每件产品的销售价定为35元时,此时每日的销售利润是:(35﹣10)(﹣35+40)=25×5=125(元),
即当每件产品的销售价定为35元时,此时每日的销售利润是125元
一.选择题(共12小题,满分36分,每小题3分)
1.(3分)式子中,x的取值范围是( )
A.x≤3 B.x≥3 C.x>3 D.x≥3且x≠4
2.(3分)下列式子为最简二次根式的是( )
A. B. C. D.
3.(3分)下列长度的三条线段能组成直角三角形的是( )
A.5,11,12 B.3,4,5 C.4,6,8 D.6,12,13
4.(3分)某中学为了让学生的跳远在中考体育测试中取得满意的成绩,在锻炼一个月后,学校对九年级一班的45名学生进行测试
跳远成绩(cm)
160
170
180
190
200
220
人数
3
9
6
9
15
3
这些运动员跳远成绩的中位数和众数分别是( )
A.190,200 B.9,9 C.15,9 D.185,200
5.(3分)下列命题中,正确的是( )
A.四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线相等的菱形是正方形
6.(3分)如图为正比例函数y=kx(k≠0)的图象,则一次函数y=x+k的大致图象是( )
A. B.
C. D.
7.(3分)下列方程一定是一元二次方程的是( )
A.3x2+﹣1=0 B.5x2﹣6y﹣3=0 C.ax2﹣x+2=0 D.3x2﹣2x﹣1=0
8.(3分)在四边形ABCD中,点E、F、G、H分别是AB、BC、CD、AD的中点,下列条件中能使四边形EFGH为矩形的是( )
A.AB⊥BC B.AB=BC C.AC⊥BD D.AC=BD
9.(3分)已知点A(a,)是两函数y=kx﹣2与图象的交点.则实数k等于( )
A. B. C. D.1
10.(3分)设x1,x2是一元二次方程x2﹣2x﹣3=0的两根,则x1+x2=( )
A.﹣2 B.2 C.3 D.﹣3
11.(3分)已知A,B两地相距120千米,甲、乙两人沿同一条公路从A地出发到B地,甲骑摩托车,图中DE(单位:千米)与时间t(单位:小时)的函数关系的图象,甲、乙两人相距y(单位:千米),则y关于t的函数图象是( )
A. B.
C. D.
12.(3分)如图,正方形ABCD中,AB=3,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G
①点G是BC的中点;
②FG=FC;
③AG∥CF;
④S△FGC=.
其中正确结论是( )
A.①② B.②④ C.①②③ D.①③④
二.填空题(共4小题,满分16分,每小题4分)
13.(4分)某校九年级甲、乙两个班的期末数学平均成绩都为89分,且甲班期末数学成绩的方差为S甲2=0.02(分2),乙班期末数学成绩的方差为S乙2=1.2(分2),则期末数学成绩 班更稳定.(填甲或乙)
14.(4分)一次函数y=(m﹣3)x﹣2的图象经过二、三、四象限,则m的取值范围是 .
15.(4分)已知:一元二次方程x2﹣6x+c=0有一个根为2,则另一根为 .
16.(4分)如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处cm,且tan∠EFC= .
三.解答题(共7小题,满分68分)
17.(10分)(1)计算:﹣﹣+(﹣1)0.
(2)解方程:x2﹣6x+9=4.
18.(10分)为了让广大青少年学生走向操场、走进自然、走到阳光下,积极参加体育锻炼,我国启动了“全国亿万学生阳光体育运动”.短跑运动,增强人的爆发力,因此小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示
(1)请根据图中信息,补齐下面的表格;
第1次
第2次
第3次
第4次
第5次
小明
13.3
13.4
13.3
13.3
小亮
13.2
13.1
13.5
13.3
(2)分别计算他们的平均数、极差和方差,若你是他们的教练,将小明与小亮的成绩比较后
19.(10分)如图,在?ABCD中,E,F分别为边AB,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,请证明四边形BEDF是菱形.
20.(8分)某钢铁厂计划今年第一季度一月份的总产量为500t,三月份的总产量为720t,若平均每月的增长率相同.
(1)第一季度平均每月的增长率;
(2)如果第二季度平均每月的增长率保持与第一季度平均每月的增长率相同,请你估计该厂今年5月份总产量能否突破1000t?
21.(8分)已知关于x 的一元二次方程x2﹣5x+m=0.
(1)若方程有实数根,求实数m 的取值范围;
(2)若方程两实数根为x1,x2,且满足3x1﹣2x2=5,求实数m 的值.
22.(10分)直线l经过(2,3)和(﹣2,﹣1)两点,它还与x轴交于A点,与经过原点的直线OB交于第三象限的B点,且∠ABO=30°.求:
(1)点A、C的坐标;
(2)点B的坐标.
23.(12分)某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)
x/元
…
15
20
25
…
y/件
…
25
20
15
…
已知日销售量y是销售价x的一次函数.
(1)求日销售量y(件)与每件产品的销售价x(元)之间的函数表达式;
(2)当每件产品的销售价定为35元时,此时每日的销售利润是多少元?
参考答案
一.选择题(共12小题,满分36分,每小题3分)
1.解:由题意得:,
解得:x≥3且x≠6.
故选:D.
2.解:A、=|a+b|,故本选项不符合题意;
B、=2,故本选项不符合题意;
C、是最简二次根式;
D、=,不是最简二次根式;
故选:C.
3.解:A、因为52+118≠122,所以三条线段不能组成直角三角形;
B、因为34+42=42,所以三条线段能组成直角三角形;
C、因为47+62≠42,所以三条线段不能组成直角三角形;
D、因为65+122≠132,所以三条线段不能组成直角三角形.
故选:B.
4.解:在这一组数据中200是出现次数最多的,
故众数是200cm;
在这45个数中,处于中间位置的第23个数是190.
所以这些学生跳远成绩的中位数和众数分别是190,200.
故选:A.
5.解:A,错误;
B,错误,但不是正方形;
C,错误;
D,正确;
故选:D.
6.解:因为正比例函数y=kx(k≠0)的图象经过第二、四象限,
所以k<0,
所以一次函数y=x+k的图象经过一、三、四象限,
故选:B.
7.解:A、是分式方程;
B、是二元二次方程;
C、a=0时,故C错误;
D、是一元二次方程;
故选:D.
8.证明:∵点E、F、G、H分别是边AB、CD,
∴EF=ACAC,
∴EF=GH,同理EH=FG
∴四边形EFGH是平行四边形;
当对角线AC、BD互相垂直时,
∴EF与FG垂直.
∴四边形EFGH是矩形.
故选:C.
9.解:∵A(a,)是两函数y=kx﹣2与,
∴A(a,)满足两函数的解析式y=kx﹣7与,
∴,
解得,.
故选:D.
10.解:根据根与系数的关系,
x1+x2=﹣=2.
故选:B.
11.解:由题意和图象可得,乙到达B地时甲距A地120km;
甲的速度是:120÷(3﹣1)=60km/h,乙的速度是:80÷4=;
设乙出发后被甲追上的时间为xh,则60(x﹣4)=x,即乙出发后被甲追上的时间为1.5h.
所以符合题意的函数图象只有选项B.
故选:B.
12.解:∵四边形ABCD是正方形,
∴AB=AD=DC=3,∠B=D=90°,
∵CD=3DE,
∴DE=8,
∵△ADE沿AE折叠得到△AFE,
∴DE=EF=1,AD=AF,
∴AF=AB,
在Rt△ABG和Rt△AFG中,
,
∴Rt△ABG≌Rt△AFG(HL),
∴BG=FG,∠AGB=∠AGF,
设BG=x,则CG=BC﹣BG=3﹣x,
在Rt△ECG中,由勾股定理得:CG2+CE2=EG2,
∵CG=3﹣x,CE=2,
∴(3﹣x)4+22=(x+4)2
解得:x=1.8,
∴BG=GF=CG=1.5,①正确;
∴∠CFG=∠FCG,
∵∠BGF=∠CFG+∠FCG,
又∵∠BGF=∠AGB+∠AGF,
∴∠CFG+∠FCG=∠AGB+∠AGF,
∵∠AGB=∠AGF,∠CFG=∠FCG,
∴∠AGB=∠FCG,
∴AG∥CF,③正确;
∵△CFG和△CEG中,分别把FG和GE看作底边,
则这两个三角形的高相同.
∴===,
∵S△GCE=×1.4×2=1.4,
∴S△CFG=×8.5=;
正确的结论是①③④,
故选:D.
二.填空题(共4小题,满分16分,每小题4分)
13.解:因为九年级甲、乙两个班的期末数学平均成绩都为89分甲2=0.02<S乙2=1.2,方差小的为甲,
所以期末数学成绩甲班更稳定.
故答案为:甲.
14.解:∵一次函数y=(m﹣3)x﹣2的图象经过二、三、四象限,
∴m﹣7<0,
∴m<3,
故答案为:m<3
15.解:设方程另一根为t,
根据题意得2+t=6,
解得t=5.
故答案为4.
16.解:设CE=3k,则CF=4k,
∴DC=AB=5k,
∵∠AFB+∠BAF=90°,∠AFB+∠EFC=90°,
∴∠BAF=∠EFC,
∴tan∠BAF=tan∠EFC=,
∴BF=7k,AF=BC=AD=10k,
在Rt△AFE中由勾股定理得AE===5,
解得:k=3,
故矩形ABCD的周长=2(AB+BC)=2(7k+10k)=36cm.
三.解答题(共7小题,满分68分)
17.解:(1)原式=3﹣﹣+1=;
(2)∵x2﹣6x+2=4,
∴(x﹣3)5=4,
则x﹣3=±5,
∴x1=5,x5=1.
18.解:(1)
第1次
第2次
第4次
第4次
第5次
小明
13.6
13.4
13.3
13.4
13.3
小亮
13.2
13.7
13.1
13.5
13.7
(2)小明:平均分为13.3,
极差为0.3,
方差为0.004,
小亮:平均分为13.3,
极差为8.4,
方差为0.02,
∵S7小明<S2小亮,
∴小明同学的成绩较为稳定,但是他的最高成绩没有小亮高,有待提高.
而小亮同学爆发力还行,但是成绩不稳定.
19.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,
∵E、F分别为边AB,
∴AE=ABCD,
∴AE=CF,
在△ADE和△CBF中,
∵,
∴△ADE≌△CBF(SAS).
(2)证明:∵E、F分别为边AB,
∴DF=DCAB,
又∵在?ABCD中,AB∥CD,
∴DF∥BE,DF=BE,
∴四边形DEBF为平行四边形,
∵DB⊥BC,
∴∠DBC=90°,
∴△DBC为直角三角形,
又∵F为边DC的中点,
∴BF=DC=DF,
又∵四边形DEBF为平行四边形,
∴四边形DEBF是菱形.
20.解:(1)设第一季度平均每月的增长率为x,
根据题意得:500(1+x)2=720,
解得:x5=0.2=20%,x5=﹣2.2(舍去).
答:第一季度平均每月的增长率为20%.
(2)720×(5+20%)2=1036.8(t),
∵1036.8>1000,
∴该厂今年5月份总产量能突破1000t.
21.解:(1)∵方程有实数根,
∴△=25﹣4m≥0,
解得,m≤;
(2)由一元二次方程根与系数的关系可知,x1+x2=2,x1?x2=m,
∵2x1﹣2x8=5,
∴3x5+3x2﹣3x2=5,
∴﹣5x2=﹣10,
解得,x2=8,
把x=2代入原方程得,m=6.
22.解:(1)设直线l的解析式为:y=kx+b,
则,
解得:,
∴直线l的解析式为:y=x+1,
则点A的坐标(﹣1,8),1).
(2)作OD⊥AC于D,BF⊥y轴于F,
∵OA=1,OC=2,
∴AC=,
则OD=AD=CD=,
在Rt△BOD中,∠ABO=30°,
BD=,则BC=,
|BF|=|CF|=?=,
|OF|=﹣1=,
∵B在第三象限,
∴点B的坐标为:(﹣,﹣).
23.解:(1)设日销售量y(件)与每件产品的销售价x(元)之间的函数表达式是y=kx+b,
,
解得,,
即日销售量y(件)与每件产品的销售价x(元)之间的函数表达式是y=﹣x+40;
(2)当每件产品的销售价定为35元时,此时每日的销售利润是:(35﹣10)(﹣35+40)=25×5=125(元),
即当每件产品的销售价定为35元时,此时每日的销售利润是125元
同课章节目录
