1.4.1 空间中点、直线和平面的向量表示课件-2020-2021学年高二数学人教A版(2019)选择性必修第一册(13张PPT)
文档属性
| 名称 | 1.4.1 空间中点、直线和平面的向量表示课件-2020-2021学年高二数学人教A版(2019)选择性必修第一册(13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 197.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-22 00:00:00 | ||
图片预览





文档简介
1.4.1
用空间向量研究直线、平面的位置关系
1.空间中点、直线和平面的向量表示
引入
我们已经把向量从平面推广到空间,并利用空间向量解决了一些有关空间位置关系和度量的问题,我们发现建立空间向量与几何要素的对应关系是利用空间向量解决立体几何问题的关键,本节我们进一步运用空间向量研究立体几何中有关直线、平面的位置关系和度量问题。
点、直线、平面是空间中的基本图形,为了用空间向量解决立体几何问题,首先要用向量表示空间中的点、直线、平面?
思考1
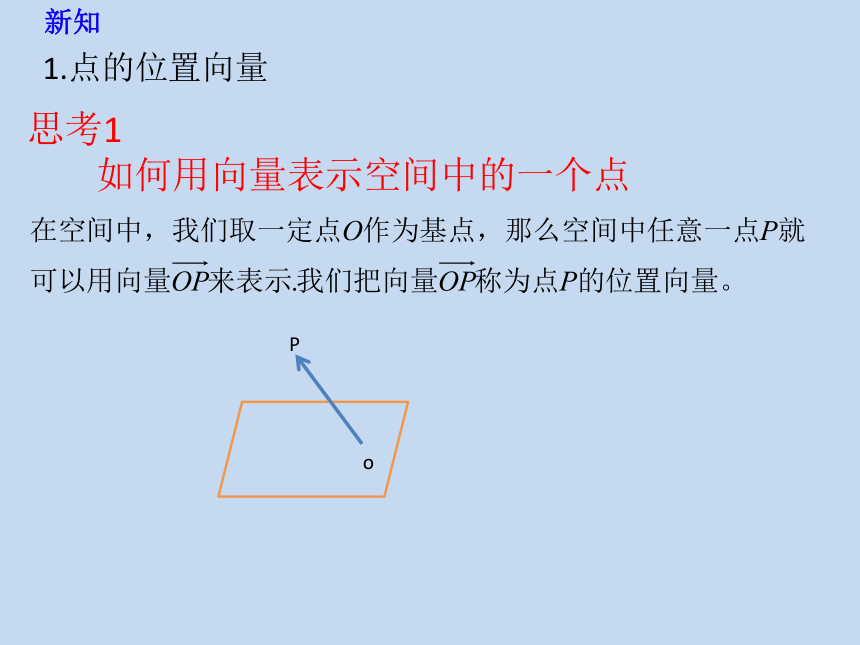
如何用向量表示空间中的一个点
P
o
1.点的位置向量
新知
思考2:我们知道,空间中给定一个点A和一个方向就能唯一确定一条直线l,如何向量表示直线 l?
2、空间直线的向量表示式
新知
3、空间平面的向量表达式
思考3:一个定点和两个定方向,能否确定一个平面?如果能确定,如何用向量表示这个平面?
新知
思考4:进一步地,一个定点和一个定方向,能否确定一个平面。如果能确定,如何用向量表示这个平面?
新知
4、平面的法向量
练习
1、判断下列命题是否正确
(1)零向量不能作为直线的方向向量和平面的法向量。
( )
(2)若v是直线l的方向向量,则λv(λ∈R)也是直线l的方向向量。 ( )
(3)在空间直角坐标系中,j=(0,0,1)是坐标平面Oxy的一个法向量。 ( )
2、若点A(-1,0,1),B(1,4,7)在直线l上,则直线l的一个方向向量的坐标可以是______________.
(2,4,6)
?
×
?
x
y
z
例1.已知长方体ABCD?A1B1C1D1中,AB=4,BC=3,CC1 =2,M为AB中点.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立如图所示空间直角坐标系,
(1)求平面BCC1B1的一个法向量.
(2)求平面MCA1的一个法向量.
A1
D1
C1
B1
A
C
B
O
M
例题
解:(1)因为y轴垂直于平面BCC1B1
所以n1=(0,1,0)是平面BCC1B1的一个法向量
x
y
z
例1.已知长方体ABCD?A1B1C1D1中,AB=4,BC=3,CC1 =2,M为AB中点.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立如图所示空间直角坐标系,
(1)求平面BCC1B1的一个法向量.
(2)求平面MCA1的一个法向量.
A1
D1
C1
B1
A
C
B
O
M
例题
归纳求平面法向量的步骤:
①设出平面的法向量为n=(x,y,z)
②找平面内的两个不共线的向量的坐标
③依据法向量的定义建立关于x,y,z的方程组
④解方程组,赋值,取其中的一个解,即得法向量,
归纳
练习
解:以D为原点,DA,DC,DD1所在直线为坐标轴建立空间直角坐标系(如图所示).
小结
1、空间中点、直线和平面的向量表示
点→点+位置向量
线→点+方向向量
平面→点+法向量
2、归纳求平面法向量的步骤:
①设出平面的法向量为n=(x,y,z)
②找平面内的两个不共线的向量的坐标
③依据法向量的定义建立关于x,y,z的方程组
④解方程组,赋值,取其中的一个解,即得法向量,
作业
课本P29 练习 3
用空间向量研究直线、平面的位置关系
1.空间中点、直线和平面的向量表示
引入
我们已经把向量从平面推广到空间,并利用空间向量解决了一些有关空间位置关系和度量的问题,我们发现建立空间向量与几何要素的对应关系是利用空间向量解决立体几何问题的关键,本节我们进一步运用空间向量研究立体几何中有关直线、平面的位置关系和度量问题。
点、直线、平面是空间中的基本图形,为了用空间向量解决立体几何问题,首先要用向量表示空间中的点、直线、平面?
思考1
如何用向量表示空间中的一个点
P
o
1.点的位置向量
新知
思考2:我们知道,空间中给定一个点A和一个方向就能唯一确定一条直线l,如何向量表示直线 l?
2、空间直线的向量表示式
新知
3、空间平面的向量表达式
思考3:一个定点和两个定方向,能否确定一个平面?如果能确定,如何用向量表示这个平面?
新知
思考4:进一步地,一个定点和一个定方向,能否确定一个平面。如果能确定,如何用向量表示这个平面?
新知
4、平面的法向量
练习
1、判断下列命题是否正确
(1)零向量不能作为直线的方向向量和平面的法向量。
( )
(2)若v是直线l的方向向量,则λv(λ∈R)也是直线l的方向向量。 ( )
(3)在空间直角坐标系中,j=(0,0,1)是坐标平面Oxy的一个法向量。 ( )
2、若点A(-1,0,1),B(1,4,7)在直线l上,则直线l的一个方向向量的坐标可以是______________.
(2,4,6)
?
×
?
x
y
z
例1.已知长方体ABCD?A1B1C1D1中,AB=4,BC=3,CC1 =2,M为AB中点.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立如图所示空间直角坐标系,
(1)求平面BCC1B1的一个法向量.
(2)求平面MCA1的一个法向量.
A1
D1
C1
B1
A
C
B
O
M
例题
解:(1)因为y轴垂直于平面BCC1B1
所以n1=(0,1,0)是平面BCC1B1的一个法向量
x
y
z
例1.已知长方体ABCD?A1B1C1D1中,AB=4,BC=3,CC1 =2,M为AB中点.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立如图所示空间直角坐标系,
(1)求平面BCC1B1的一个法向量.
(2)求平面MCA1的一个法向量.
A1
D1
C1
B1
A
C
B
O
M
例题
归纳求平面法向量的步骤:
①设出平面的法向量为n=(x,y,z)
②找平面内的两个不共线的向量的坐标
③依据法向量的定义建立关于x,y,z的方程组
④解方程组,赋值,取其中的一个解,即得法向量,
归纳
练习
解:以D为原点,DA,DC,DD1所在直线为坐标轴建立空间直角坐标系(如图所示).
小结
1、空间中点、直线和平面的向量表示
点→点+位置向量
线→点+方向向量
平面→点+法向量
2、归纳求平面法向量的步骤:
①设出平面的法向量为n=(x,y,z)
②找平面内的两个不共线的向量的坐标
③依据法向量的定义建立关于x,y,z的方程组
④解方程组,赋值,取其中的一个解,即得法向量,
作业
课本P29 练习 3
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
