1.4.1 (2)空间中直线、平面的平行课件-2020-2021学年高二数学上学期数学人教A版(2019)选择性必修第一册(17张PPT)
文档属性
| 名称 | 1.4.1 (2)空间中直线、平面的平行课件-2020-2021学年高二数学上学期数学人教A版(2019)选择性必修第一册(17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 371.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-22 23:44:30 | ||
图片预览




文档简介
1.4.1
用空间向量研究直线、平面的位置关系
2.空间中直线、平面的平行
空间中直线的方向向量、平面的法向量是确定空间中的直线、平面的关键量,能否用直线的方向向量、平面的法向量来刻画直线、平面的平行关系?
引入
思考
1:如何用直线的方向向量表示两条直线的平行?
新知
l1
l2
u1
u2
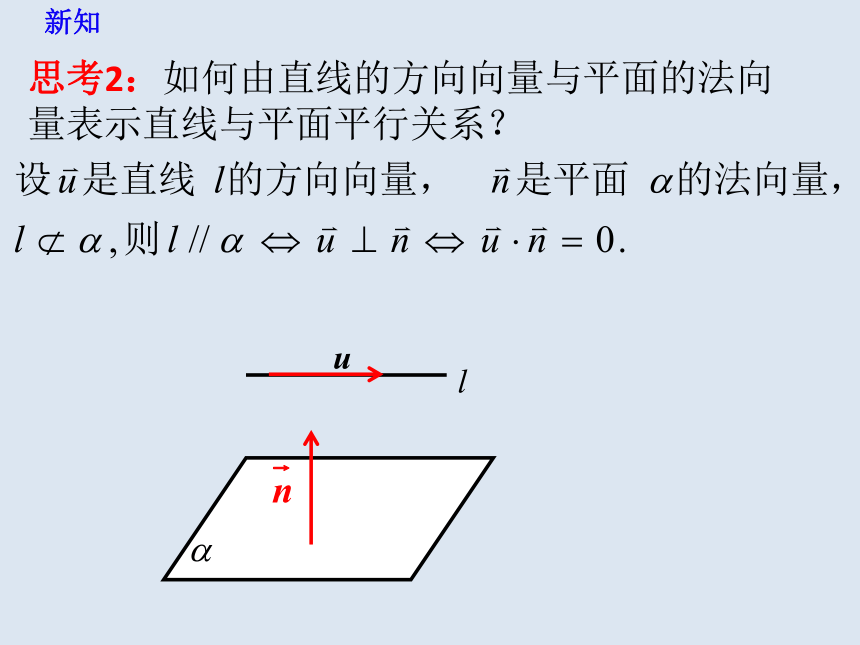
思考2:如何由直线的方向向量与平面的法向量表示直线与平面平行关系?
新知
l
u
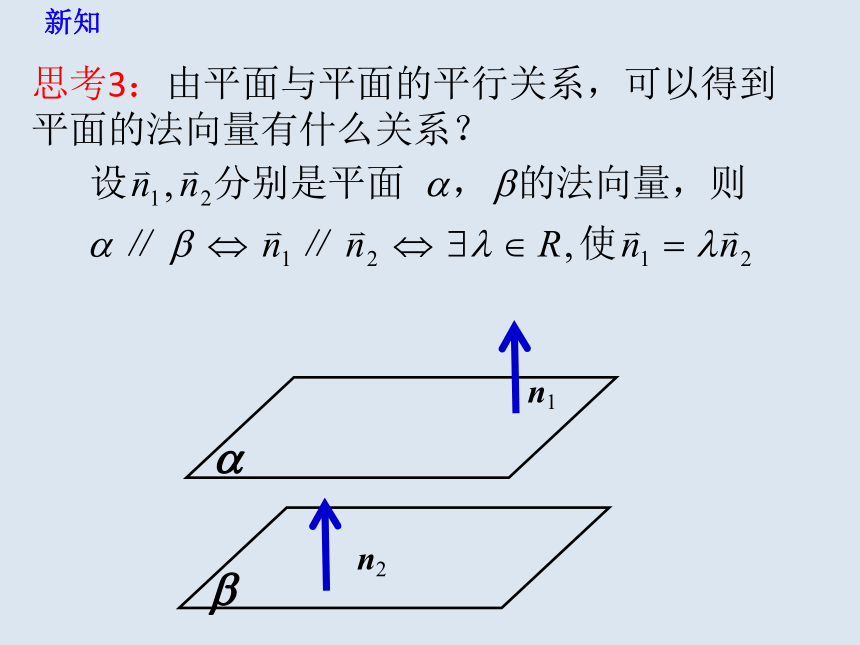
思考3:由平面与平面的平行关系,可以得到平面的法向量有什么关系?
新知
n1
n2
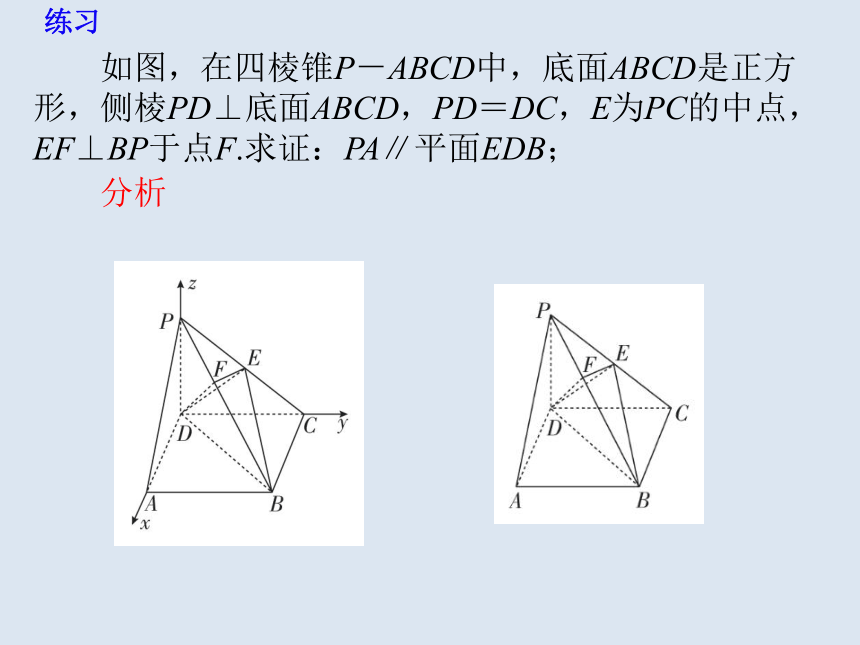
练行
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E为PC的中点,EF⊥BP于点F.求证:PA∥平面EDB;
练习
分析
练习
y
z
x
A1
D1
C1
B1
A
C
B
O
P
例题
y
z
x
A1
D1
C1
B1
A
C
B
O
P
例题
还有证明其他方法求P吗?
y
z
x
A1
D1
C1
B1
A
C
B
O
P
例题
y
z
x
A1
D1
C1
B1
A
C
B
O
P
例题
归纳:利用向量解决探索性问题的方法
对于探索性问题,一般先假设存在,利用空间坐标系,结合已知条件,转化为代数方程是否有解的问题.
若有解满足题意,则存在;若没有满足题意的解,则不存在.
如图,直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4.在AB上是否存在点D,使得AC1∥平面CDB1.
例题
a
b
P
例2 证明“平面与平面平行的判定定理”:若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
例题
小结
2、利用向量解决探索性问题的方法
对于探索性问题,一般先假设存在,利用空间坐标系,结合已知条件,转化为代数方程是否有解的问题.
若有解满足题意,则存在;若没有满足题意的解,则不存在.
作业
课本P31
练习
2、3
用空间向量研究直线、平面的位置关系
2.空间中直线、平面的平行
空间中直线的方向向量、平面的法向量是确定空间中的直线、平面的关键量,能否用直线的方向向量、平面的法向量来刻画直线、平面的平行关系?
引入
思考
1:如何用直线的方向向量表示两条直线的平行?
新知
l1
l2
u1
u2
思考2:如何由直线的方向向量与平面的法向量表示直线与平面平行关系?
新知
l
u
思考3:由平面与平面的平行关系,可以得到平面的法向量有什么关系?
新知
n1
n2
练行
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E为PC的中点,EF⊥BP于点F.求证:PA∥平面EDB;
练习
分析
练习
y
z
x
A1
D1
C1
B1
A
C
B
O
P
例题
y
z
x
A1
D1
C1
B1
A
C
B
O
P
例题
还有证明其他方法求P吗?
y
z
x
A1
D1
C1
B1
A
C
B
O
P
例题
y
z
x
A1
D1
C1
B1
A
C
B
O
P
例题
归纳:利用向量解决探索性问题的方法
对于探索性问题,一般先假设存在,利用空间坐标系,结合已知条件,转化为代数方程是否有解的问题.
若有解满足题意,则存在;若没有满足题意的解,则不存在.
如图,直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4.在AB上是否存在点D,使得AC1∥平面CDB1.
例题
a
b
P
例2 证明“平面与平面平行的判定定理”:若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
例题
小结
2、利用向量解决探索性问题的方法
对于探索性问题,一般先假设存在,利用空间坐标系,结合已知条件,转化为代数方程是否有解的问题.
若有解满足题意,则存在;若没有满足题意的解,则不存在.
作业
课本P31
练习
2、3
