六年级下册数学课件 二 比例尺 复习浙教版25张ppt
文档属性
| 名称 | 六年级下册数学课件 二 比例尺 复习浙教版25张ppt |

|
|
| 格式 | pptx | ||
| 文件大小 | 496.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-22 00:00:00 | ||
图片预览








文档简介
二 比例尺 复习课件
知识结构
认识比例尺
比例尺的应用
位置与方法
比例尺
一幅图的图上距离和实际距离的比,叫做这幅图的比例尺。
比例尺及其应用
1、比例尺的意义:
要点一
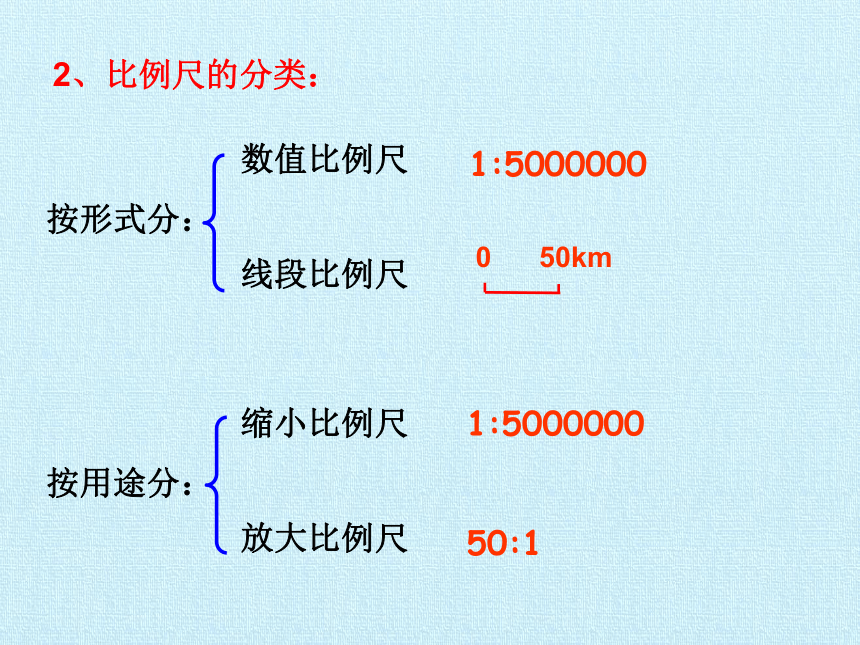
数值比例尺
线段比例尺
1:5000000
0 50km
按形式分:
缩小比例尺
放大比例尺
按用途分:
1:5000000
50:1
2、比例尺的分类:
1、图形的放大与缩小的特点是:
形状相同,大小不同。
2、图形的放大或缩小的方法:
一看,二算,三画。
图形的放大与缩小
(1)比例尺与一般的尺不同,它是一个比,不能带有计量单位;
(2)求比例尺时,前、后项的单位长度一定要统一成同级单位;
(3)比例尺的前项或后项,一般应化简成“1”。
强调
在应用比例尺解决问题时:
一般把未知数的单位设成厘米。
求实际距离时,要先计算再化单位。
求图上距离时,要先化单位再计算。
比例尺的应用
(1)无论是计算比例尺、计算实际距离,还是计算图上距离,都要统一成最小的长度单位。这样方便一些。
(2)计算实际距离和计算图上距离时,比例尺最好写成分数形式,这样可以把比例尺当作一个分数。
比例尺的应用
用、上、下、前、后、左、右确定位置。
可以用方向和距离确定位置。
用东西南北表示物体之间的位置关系。
还可以用数对来表示位置。
位置与方向
要点二
确定位置和方向
1.用“上、下、前、后、左、右”描述物体的相对位置。
2.用“东、南、西、北、东南、东北、西南、西北”表示位置。
基本方向:在地图或者平面图上,通常上北、下南、左西、右东,还有东南、东北、西南、西北。
东
西
北
南
45。
北偏西45。
东偏南45。
45。
45。
45。
东偏北45。
西偏南45。
根据物体的方向和距离确定物体的位置的三要素:观测点、方向、距离。
根据物体的方向和距离确定物体的位置。
具体确定物体位置的方法如下:
(1)以观测点为中心,画一个表示东西南北四个方向的“十字”,并分别标出东西南北四个方位。
(4)用方向和距离这两个条件合起来就能精确地确定平面内物体的位置。物体的位置关系是相对的。物体的位置和观测点有关,观测点不同,物体位置的表述也就不同。
(2)把观测点和观测目标连起来,这样就有一个角,然后测量出于正南或正北或正东或正西方向夹角的度数。
(3)测量出观测点到观测目标之间的长度。
(3)弄清图中从哪儿按什么方向走,走多远,走到哪儿。描述简单的路线图时,,先要明确行走的方向,确定角度,确定距离;再用“先向……再向……最后向……”描述出来。
路线图
(2)根据比例尺和测量的图上距离求出相应的实际距离;
(1)根据方向标弄清路线图的方向;
1.看懂并描述路线图。
(4)以某一地点为起点,根据方向和图上距离确定下一个地点的位置,再以下一个地点为起点继续画。
路线图
(3)求出图上距离;
(2)根据实际距离及图纸的大小确定比例尺;
(1)确定方向;
2.画路线图。
1、填空。
图上距离
实际距离
比例尺
( ) ( )=实际距离
( ) ( )=图上距离
比例尺
÷
×
图上距离
实际距离
基本练习
一栋楼房东西方向长40m,在图纸上的长度是50cm,这幅图纸的比例尺是多少?
基本练习一
巩固练习:
在一幅地图上,用2厘米表示实际距离12千米,这张地图的比例尺是多少?
兰州到乌鲁木齐的铁路线大约长1900km。地图上两地之间的长度是多少厘米?(比例尺1:400000)
基本练习二
巩固练习:
甲、乙两城的实际距离是500千米,如果画在比例尺是1:4000000的地图上,应该画多少厘米?
在比例尺是1︰5000000的云南地图上,量得大理到楚雄的距离是3.2厘米。计算一下,大理到楚雄的实际距离大约是多少千米?
基本练习三
巩固练习:
在比例尺是1:400000的地图上,量得A、B两地的距离是24厘米,A、B两地的实际距离是多少千米?
基本练习四
在一张1:500的设计图纸上,量得一正方形建筑的边长是20cm,这个建筑物的实际占地面积是多少平方米?
巩固练习:
在一个比例尺是1:10000的图纸上测量一个长方形,长7.5cm,宽2.5cm,这个长方形实际面积是多少平方米?
谢 谢
知识结构
认识比例尺
比例尺的应用
位置与方法
比例尺
一幅图的图上距离和实际距离的比,叫做这幅图的比例尺。
比例尺及其应用
1、比例尺的意义:
要点一
数值比例尺
线段比例尺
1:5000000
0 50km
按形式分:
缩小比例尺
放大比例尺
按用途分:
1:5000000
50:1
2、比例尺的分类:
1、图形的放大与缩小的特点是:
形状相同,大小不同。
2、图形的放大或缩小的方法:
一看,二算,三画。
图形的放大与缩小
(1)比例尺与一般的尺不同,它是一个比,不能带有计量单位;
(2)求比例尺时,前、后项的单位长度一定要统一成同级单位;
(3)比例尺的前项或后项,一般应化简成“1”。
强调
在应用比例尺解决问题时:
一般把未知数的单位设成厘米。
求实际距离时,要先计算再化单位。
求图上距离时,要先化单位再计算。
比例尺的应用
(1)无论是计算比例尺、计算实际距离,还是计算图上距离,都要统一成最小的长度单位。这样方便一些。
(2)计算实际距离和计算图上距离时,比例尺最好写成分数形式,这样可以把比例尺当作一个分数。
比例尺的应用
用、上、下、前、后、左、右确定位置。
可以用方向和距离确定位置。
用东西南北表示物体之间的位置关系。
还可以用数对来表示位置。
位置与方向
要点二
确定位置和方向
1.用“上、下、前、后、左、右”描述物体的相对位置。
2.用“东、南、西、北、东南、东北、西南、西北”表示位置。
基本方向:在地图或者平面图上,通常上北、下南、左西、右东,还有东南、东北、西南、西北。
东
西
北
南
45。
北偏西45。
东偏南45。
45。
45。
45。
东偏北45。
西偏南45。
根据物体的方向和距离确定物体的位置的三要素:观测点、方向、距离。
根据物体的方向和距离确定物体的位置。
具体确定物体位置的方法如下:
(1)以观测点为中心,画一个表示东西南北四个方向的“十字”,并分别标出东西南北四个方位。
(4)用方向和距离这两个条件合起来就能精确地确定平面内物体的位置。物体的位置关系是相对的。物体的位置和观测点有关,观测点不同,物体位置的表述也就不同。
(2)把观测点和观测目标连起来,这样就有一个角,然后测量出于正南或正北或正东或正西方向夹角的度数。
(3)测量出观测点到观测目标之间的长度。
(3)弄清图中从哪儿按什么方向走,走多远,走到哪儿。描述简单的路线图时,,先要明确行走的方向,确定角度,确定距离;再用“先向……再向……最后向……”描述出来。
路线图
(2)根据比例尺和测量的图上距离求出相应的实际距离;
(1)根据方向标弄清路线图的方向;
1.看懂并描述路线图。
(4)以某一地点为起点,根据方向和图上距离确定下一个地点的位置,再以下一个地点为起点继续画。
路线图
(3)求出图上距离;
(2)根据实际距离及图纸的大小确定比例尺;
(1)确定方向;
2.画路线图。
1、填空。
图上距离
实际距离
比例尺
( ) ( )=实际距离
( ) ( )=图上距离
比例尺
÷
×
图上距离
实际距离
基本练习
一栋楼房东西方向长40m,在图纸上的长度是50cm,这幅图纸的比例尺是多少?
基本练习一
巩固练习:
在一幅地图上,用2厘米表示实际距离12千米,这张地图的比例尺是多少?
兰州到乌鲁木齐的铁路线大约长1900km。地图上两地之间的长度是多少厘米?(比例尺1:400000)
基本练习二
巩固练习:
甲、乙两城的实际距离是500千米,如果画在比例尺是1:4000000的地图上,应该画多少厘米?
在比例尺是1︰5000000的云南地图上,量得大理到楚雄的距离是3.2厘米。计算一下,大理到楚雄的实际距离大约是多少千米?
基本练习三
巩固练习:
在比例尺是1:400000的地图上,量得A、B两地的距离是24厘米,A、B两地的实际距离是多少千米?
基本练习四
在一张1:500的设计图纸上,量得一正方形建筑的边长是20cm,这个建筑物的实际占地面积是多少平方米?
巩固练习:
在一个比例尺是1:10000的图纸上测量一个长方形,长7.5cm,宽2.5cm,这个长方形实际面积是多少平方米?
谢 谢
同课章节目录
- 一 比例
- 1、比例的意义与性质
- 2、正比例(一)
- 3、解比例
- 4、正比例(二)
- 5、正比例应用问题
- 6、反比例(一)
- 7、反比例(二)
- 8、反比例应用问题
- 二 比例尺
- 9、认识比例尺
- 10、比例尺的应用
- 11、方向与位置
- 四 圆柱与圆锥
- 16、圆柱与圆锥的认识
- 17、圆柱的表面积
- 18、圆柱的体积
- 19、圆锥的体积
- 五 整理与复习
- 20、整数与小数
- 21、数的整除
- 22、分数与百分数
- 23、加减运算
- 24、乘除运算
- 25、四则混合运算
- 26、代数式与方程
- 27、比与比例
- 28、应用问题
- 29、线与角
- 30、方向与位置
- 31、位置的确定
- 32、平面图形
- 33、图形的交换
- 34、立体图形
- 35、数据的整理
- 36、统计与可能性
- 总复习
