18.2.3 正方形-2020-2021学年人教版八年级数学下册课件(20张)
文档属性
| 名称 | 18.2.3 正方形-2020-2021学年人教版八年级数学下册课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 832.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-21 13:11:39 | ||
图片预览


文档简介
18.2.3
正方形
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在。
正方形的四条边相等,四个角都是直角
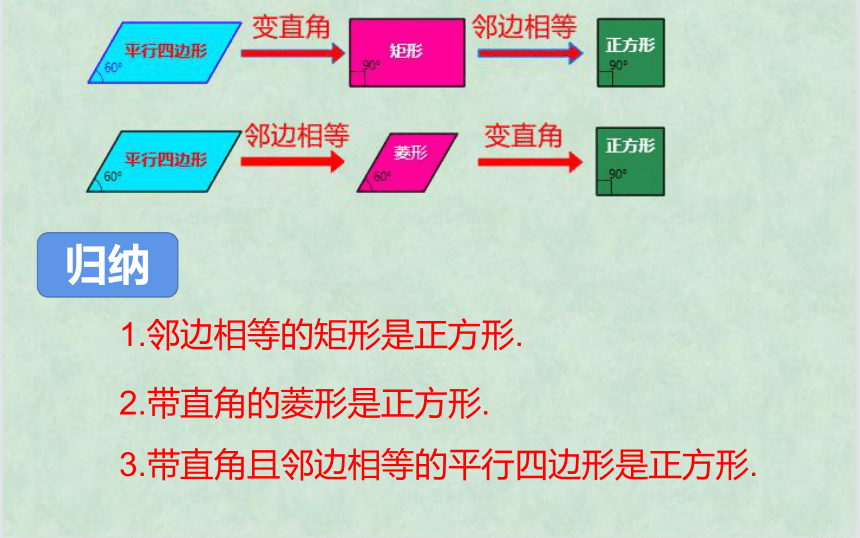
归纳
1.邻边相等的矩形是正方形.
2.带直角的菱形是正方形.
3.带直角且邻边相等的平行四边形是正方形.
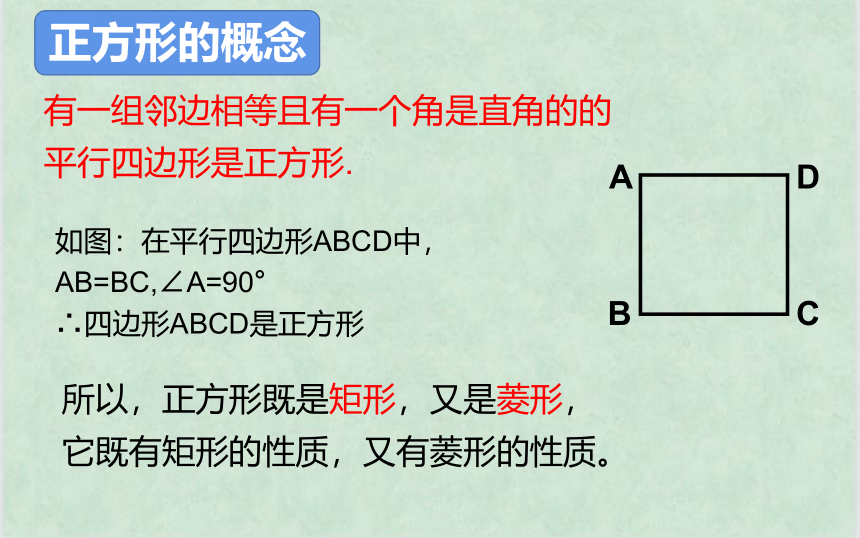
正方形的概念
有一组邻边相等且有一个角是直角的的平行四边形是正方形.
所以,正方形既是矩形,又是菱形,它既有矩形的性质,又有菱形的性质。
A
B
C
D
如图:在平行四边形ABCD中,
AB=BC,∠A=90°
∴四边形ABCD是正方形
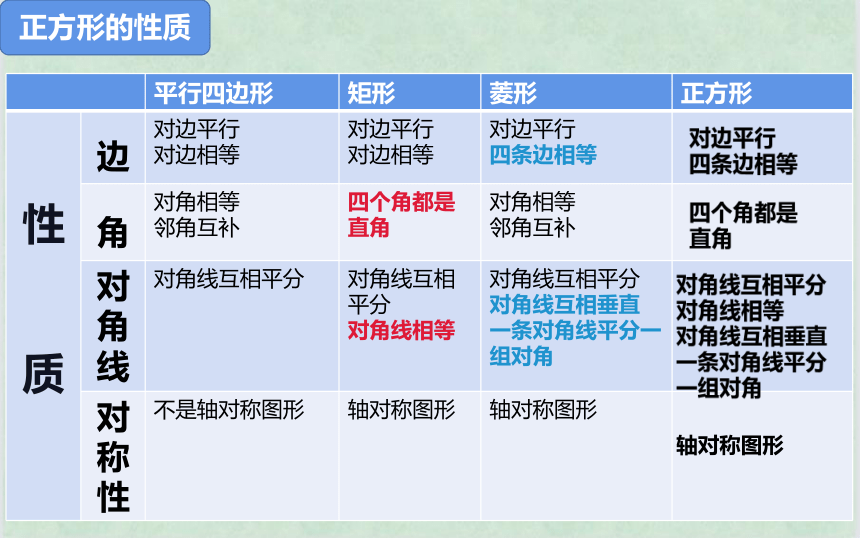
正方形的性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
平行四边形
矩形
菱形
正方形
性质
边
对边平行
对边相等
对边平行
对边相等
对边平行
四条边相等
角
对角相等
邻角互补
四个角都是直角
对角相等
邻角互补
对角线
对角线互相平分
对角线互相平分
对角线相等
对角线互相平分
对角线互相垂直
一条对角线平分一组对角
对称性
不是轴对称图形
轴对称图形
轴对称图形
对边平行
四条边相等
四个角都是直角
对角线互相平分
对角线相等
对角线互相垂直
一条对角线平分一组对角
轴对称图形
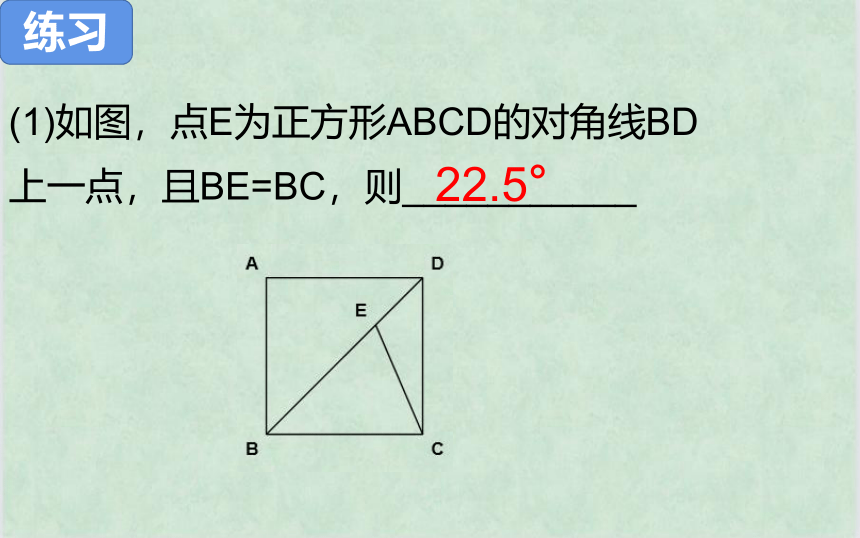
练习
(1)如图,点E为正方形ABCD的对角线BD上一点,且BE=BC,则___________
22.5°
练习
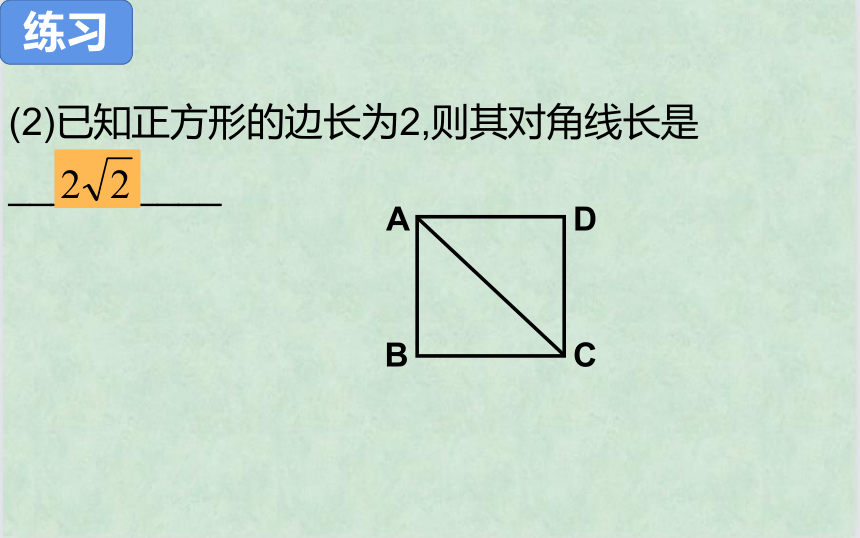
(2)已知正方形的边长为2,则其对角线长是__________
A
B
C
D
练习
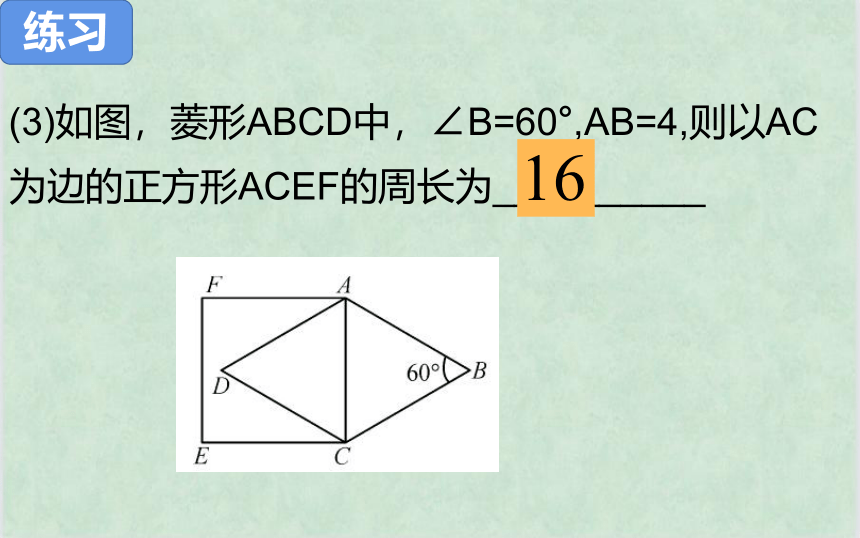
(3)如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边的正方形ACEF的周长为__________
练习
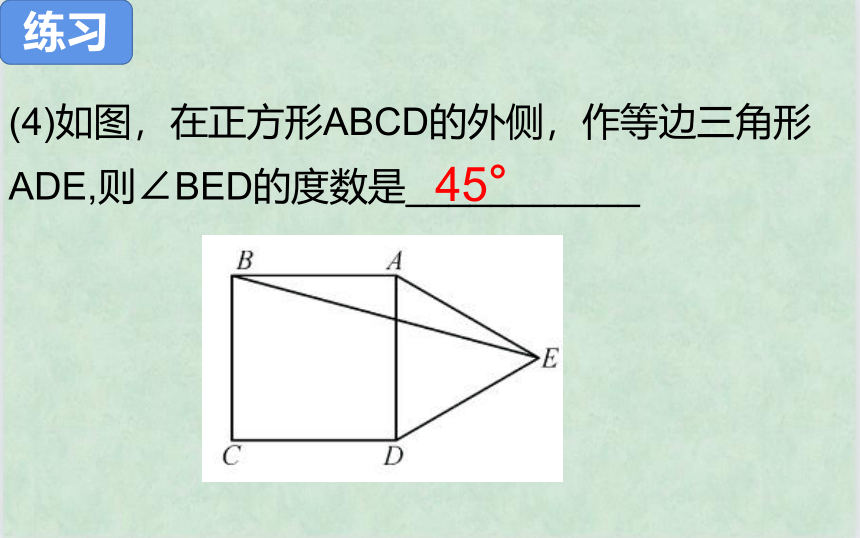
(4)如图,在正方形ABCD的外侧,作等边三角形ADE,则∠BED的度数是___________
45°
正方形的判定
定义法
判定一:有一组邻边相等,并且有一个角是直角的平行四边形是正方形.
正方形的判定
矩形菱形法
正方形既是矩形,又是菱形
一个四边形既是菱形又是矩形,那么它肯定是正方形
正方形的判定
矩形菱形法
判定二:有一组邻边相等的矩形是正方形.
判定三:对角线互相垂直的矩形是正方形.
练习
如图,在直角三角形中,∠C=90°,∠CAB、∠ABC的平分线交于D.DE⊥AC,DF⊥BC,DG⊥AB.求证:四边形CEDF为正方形.
正方形的判定
矩形菱形法
判定四:有一个角是直角的菱形是正方形.
判定五:对角线相等的菱形是正方形.
练习
在正方形ABCD中,点E、F、G、H分别在各边上,且AE=BF=CG=DH.四边形EFGH是正方形吗?为什么?
练习
已知AD是△ABC的角平分线,DE//AC交AB于E,DF//AB交AC于F,且AD=EF,求证:四边形AEDF是正方形。
正方形的判定
对角线法
判定六:对角线互相平分、垂直且相等的四边形是正方形.
练行四边形ABCD中,对角线AC与DB相交于点O.要使四边形ABCD是正方形,还需添加一组条件。下面给出了四组条件:
①AB⊥AD,且AB=AD;
②AB=BD且AB⊥BD;
③OB=OC,且OB⊥OC;
④AB=AD且AC=BD;
其中正确的是__________
①③④
正方形
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在。
正方形的四条边相等,四个角都是直角
归纳
1.邻边相等的矩形是正方形.
2.带直角的菱形是正方形.
3.带直角且邻边相等的平行四边形是正方形.
正方形的概念
有一组邻边相等且有一个角是直角的的平行四边形是正方形.
所以,正方形既是矩形,又是菱形,它既有矩形的性质,又有菱形的性质。
A
B
C
D
如图:在平行四边形ABCD中,
AB=BC,∠A=90°
∴四边形ABCD是正方形
正方形的性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
平行四边形
矩形
菱形
正方形
性质
边
对边平行
对边相等
对边平行
对边相等
对边平行
四条边相等
角
对角相等
邻角互补
四个角都是直角
对角相等
邻角互补
对角线
对角线互相平分
对角线互相平分
对角线相等
对角线互相平分
对角线互相垂直
一条对角线平分一组对角
对称性
不是轴对称图形
轴对称图形
轴对称图形
对边平行
四条边相等
四个角都是直角
对角线互相平分
对角线相等
对角线互相垂直
一条对角线平分一组对角
轴对称图形
练习
(1)如图,点E为正方形ABCD的对角线BD上一点,且BE=BC,则___________
22.5°
练习
(2)已知正方形的边长为2,则其对角线长是__________
A
B
C
D
练习
(3)如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边的正方形ACEF的周长为__________
练习
(4)如图,在正方形ABCD的外侧,作等边三角形ADE,则∠BED的度数是___________
45°
正方形的判定
定义法
判定一:有一组邻边相等,并且有一个角是直角的平行四边形是正方形.
正方形的判定
矩形菱形法
正方形既是矩形,又是菱形
一个四边形既是菱形又是矩形,那么它肯定是正方形
正方形的判定
矩形菱形法
判定二:有一组邻边相等的矩形是正方形.
判定三:对角线互相垂直的矩形是正方形.
练习
如图,在直角三角形中,∠C=90°,∠CAB、∠ABC的平分线交于D.DE⊥AC,DF⊥BC,DG⊥AB.求证:四边形CEDF为正方形.
正方形的判定
矩形菱形法
判定四:有一个角是直角的菱形是正方形.
判定五:对角线相等的菱形是正方形.
练习
在正方形ABCD中,点E、F、G、H分别在各边上,且AE=BF=CG=DH.四边形EFGH是正方形吗?为什么?
练习
已知AD是△ABC的角平分线,DE//AC交AB于E,DF//AB交AC于F,且AD=EF,求证:四边形AEDF是正方形。
正方形的判定
对角线法
判定六:对角线互相平分、垂直且相等的四边形是正方形.
练行四边形ABCD中,对角线AC与DB相交于点O.要使四边形ABCD是正方形,还需添加一组条件。下面给出了四组条件:
①AB⊥AD,且AB=AD;
②AB=BD且AB⊥BD;
③OB=OC,且OB⊥OC;
④AB=AD且AC=BD;
其中正确的是__________
①③④
