18.2.1 矩形的判定-2020-2021学年人教版八年级数学下册课件(17张)
文档属性
| 名称 | 18.2.1 矩形的判定-2020-2021学年人教版八年级数学下册课件(17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 320.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-21 13:12:07 | ||
图片预览


文档简介
18.2.1 矩形的判定
复习引入
问题1 矩形的定义是什么?
有一个角是直角的平行四边形叫做矩形.
问题2 矩形有哪些性质?
边:对边平行且相等
角:四个角都是直角
对角线:互相平分且相等
讲授新课
类比平行四边形的定义也是判定平行四边形的一种方法,那么矩形的定义也是判定矩形的一种方法.
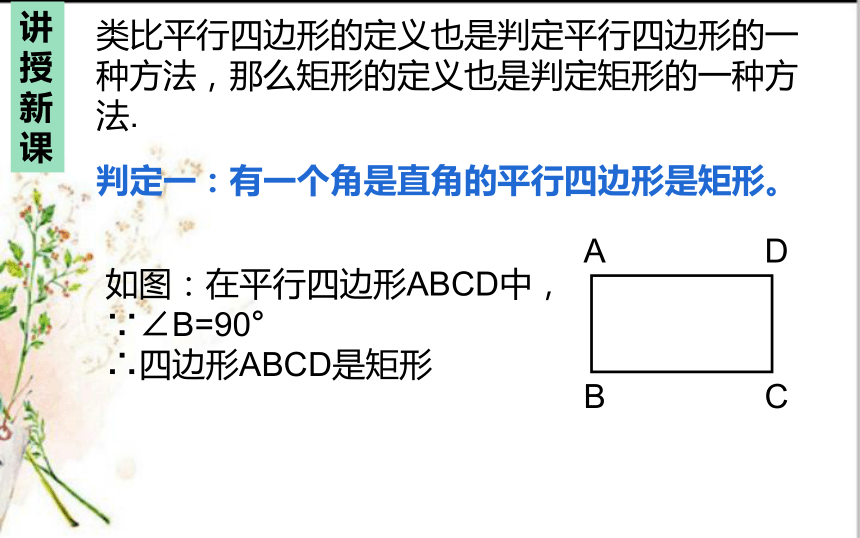
判定一:有一个角是直角的平行四边形是矩形。
A
B
C
D
如图:在平行四边形ABCD中,
∵∠B=90°
∴四边形ABCD是矩形
练习
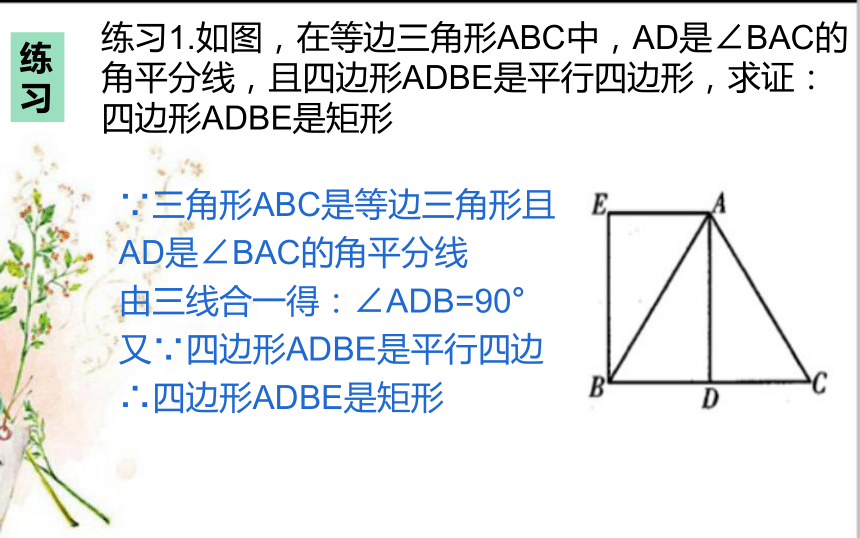
练习1.如图,在等边三角形ABC中,AD是∠BAC的角平分线,且四边形ADBE是平行四边形,求证:四边形ADBE是矩形
∵三角形ABC是等边三角形且
AD是∠BAC的角平分线
由三线合一得:∠ADB=90°
又∵四边形ADBE是平行四边
∴四边形ADBE是矩形
除了定义以外,判定矩形的方法还有没有呢?
类似地,研究矩形的性质的逆命题是否成立.
讲授新课
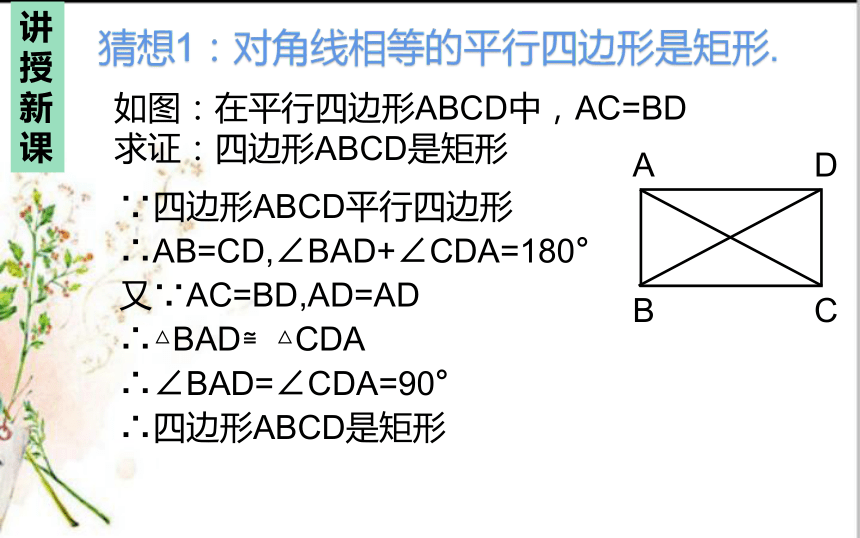
如图:在平行四边形ABCD中,AC=BD
求证:四边形ABCD是矩形
A
B
C
D
∵四边形ABCD平行四边形
∴AB=CD,∠BAD+∠CDA=180°
又∵AC=BD,AD=AD
∴△BAD≌△CDA
∴∠BAD=∠CDA=90°
∴四边形ABCD是矩形
猜想1:对角线相等的平行四边形是矩形.
讲授新课
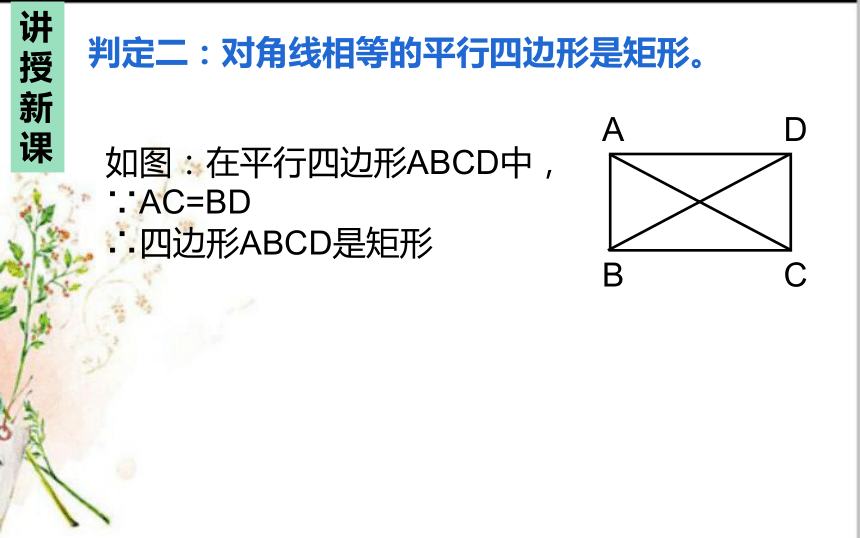
判定二:对角线相等的平行四边形是矩形。
如图:在平行四边形ABCD中,
∵AC=BD
∴四边形ABCD是矩形
A
B
C
D
讲授新课
判定三:对角线互相平分且相等的四边形是矩形。
如图:在四边形ABCD中,
∵AC=BD,AO=CO,BO=DO
∴四边形ABCD是矩形
A
B
C
D
O
练习2.如图所示,矩形AABCD的对角线相交于点O,E,F,G.H分别是AO,BO,CO,DO的中点,请问四边形EFGH是矩形吗?请说明理由.
解:四边形EFGH是矩形.
∵四边形ABCD是矩形,
∴AC=BD,AO=BO=CO=DO
∵E,F,G,H分别是AO,BO,CO,DO的中点,
∴EO=FO=GO=HO
∴OE= OG,OF=OH
∴四边形EFGH是平行四边形,
∵EO+GO=FO+ HO,即EG=FH,
∴四边形EFGH是矩形.
练习3.如图,在四边形ABCD中,AC,BD相交于点O,且AO=CO,AB//CD.
(1)求证:AB= CD;
(2)若∠OAB=∠OBA,求证:四边形ABCD是矩形.
A
B
C
D
O
练习3.如图,在四边形ABCD中,AC,BD相交于点O,且AO=CO,AB//CD.
(1)求证:AB= CD;
(2)若∠OAB=∠OBA,求证:四边形ABCD是矩形.
A
B
C
D
O
讲授新课
上节课我们研究了矩形的四个角,知道它们都是直角,它的逆命题是什么?成立吗?
逆命题:四个角是直角的四边形是矩形.
成立。
讲授新课
至少有几个角是直角的四边形是矩形?
判定四:有三个角是直角的四边形是矩形.
练习4.如图,在平行四边形ABCD中,AF,BH,CH,DF
分别是∠BAD,∠ABC,∠BCD,∠ADC的平分线。求证:四边形EFGH是矩形.
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
练习5.下列各句判定矩形的说法是否正确?
?
?
?
(4)有三个角都相等的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)对角线相等,且有一个角是直角的四边形是矩形;
练习5.下列各句判定矩形的说法是否正确?
?
?
?
复习引入
问题1 矩形的定义是什么?
有一个角是直角的平行四边形叫做矩形.
问题2 矩形有哪些性质?
边:对边平行且相等
角:四个角都是直角
对角线:互相平分且相等
讲授新课
类比平行四边形的定义也是判定平行四边形的一种方法,那么矩形的定义也是判定矩形的一种方法.
判定一:有一个角是直角的平行四边形是矩形。
A
B
C
D
如图:在平行四边形ABCD中,
∵∠B=90°
∴四边形ABCD是矩形
练习
练习1.如图,在等边三角形ABC中,AD是∠BAC的角平分线,且四边形ADBE是平行四边形,求证:四边形ADBE是矩形
∵三角形ABC是等边三角形且
AD是∠BAC的角平分线
由三线合一得:∠ADB=90°
又∵四边形ADBE是平行四边
∴四边形ADBE是矩形
除了定义以外,判定矩形的方法还有没有呢?
类似地,研究矩形的性质的逆命题是否成立.
讲授新课
如图:在平行四边形ABCD中,AC=BD
求证:四边形ABCD是矩形
A
B
C
D
∵四边形ABCD平行四边形
∴AB=CD,∠BAD+∠CDA=180°
又∵AC=BD,AD=AD
∴△BAD≌△CDA
∴∠BAD=∠CDA=90°
∴四边形ABCD是矩形
猜想1:对角线相等的平行四边形是矩形.
讲授新课
判定二:对角线相等的平行四边形是矩形。
如图:在平行四边形ABCD中,
∵AC=BD
∴四边形ABCD是矩形
A
B
C
D
讲授新课
判定三:对角线互相平分且相等的四边形是矩形。
如图:在四边形ABCD中,
∵AC=BD,AO=CO,BO=DO
∴四边形ABCD是矩形
A
B
C
D
O
练习2.如图所示,矩形AABCD的对角线相交于点O,E,F,G.H分别是AO,BO,CO,DO的中点,请问四边形EFGH是矩形吗?请说明理由.
解:四边形EFGH是矩形.
∵四边形ABCD是矩形,
∴AC=BD,AO=BO=CO=DO
∵E,F,G,H分别是AO,BO,CO,DO的中点,
∴EO=FO=GO=HO
∴OE= OG,OF=OH
∴四边形EFGH是平行四边形,
∵EO+GO=FO+ HO,即EG=FH,
∴四边形EFGH是矩形.
练习3.如图,在四边形ABCD中,AC,BD相交于点O,且AO=CO,AB//CD.
(1)求证:AB= CD;
(2)若∠OAB=∠OBA,求证:四边形ABCD是矩形.
A
B
C
D
O
练习3.如图,在四边形ABCD中,AC,BD相交于点O,且AO=CO,AB//CD.
(1)求证:AB= CD;
(2)若∠OAB=∠OBA,求证:四边形ABCD是矩形.
A
B
C
D
O
讲授新课
上节课我们研究了矩形的四个角,知道它们都是直角,它的逆命题是什么?成立吗?
逆命题:四个角是直角的四边形是矩形.
成立。
讲授新课
至少有几个角是直角的四边形是矩形?
判定四:有三个角是直角的四边形是矩形.
练习4.如图,在平行四边形ABCD中,AF,BH,CH,DF
分别是∠BAD,∠ABC,∠BCD,∠ADC的平分线。求证:四边形EFGH是矩形.
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
练习5.下列各句判定矩形的说法是否正确?
?
?
?
(4)有三个角都相等的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)对角线相等,且有一个角是直角的四边形是矩形;
练习5.下列各句判定矩形的说法是否正确?
?
?
?
