18.2.2 菱形的判定-2020-2021学年人教版八年级数学下册课件(16张)
文档属性
| 名称 | 18.2.2 菱形的判定-2020-2021学年人教版八年级数学下册课件(16张) |  | |
| 格式 | pptx | ||
| 文件大小 | 940.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-21 13:13:56 | ||
图片预览



文档简介
18.2.2 菱形的判定
菱形的性质:
1.菱形的四条边都相等,对边平行.
2.菱形的对角都相等.
3.菱形的两条对角线互相垂直平分,并且每一条对角线平分一组对角.
回顾旧识:菱形的定义是什么?性质有哪些?
菱形的定义:有一组邻边相等的平行四边形叫做菱形
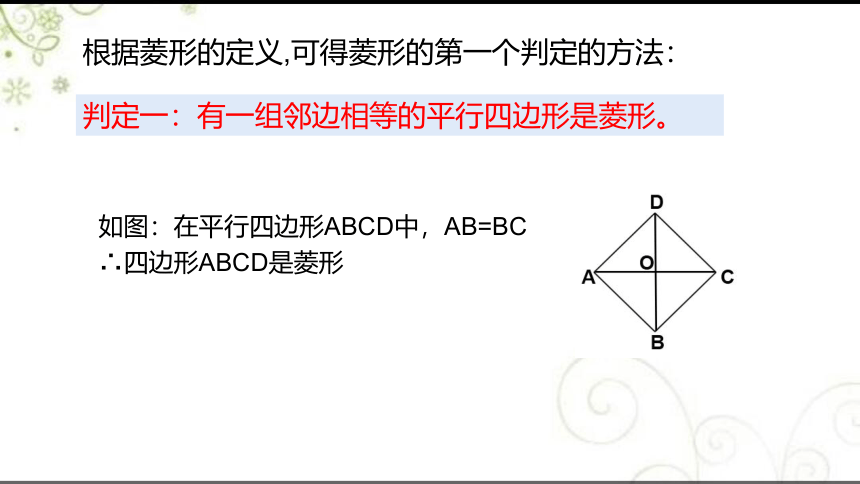
根据菱形的定义,可得菱形的第一个判定的方法:
判定一:有一组邻边相等的平行四边形是菱形。
如图:在平行四边形ABCD中,AB=BC
∴四边形ABCD是菱形
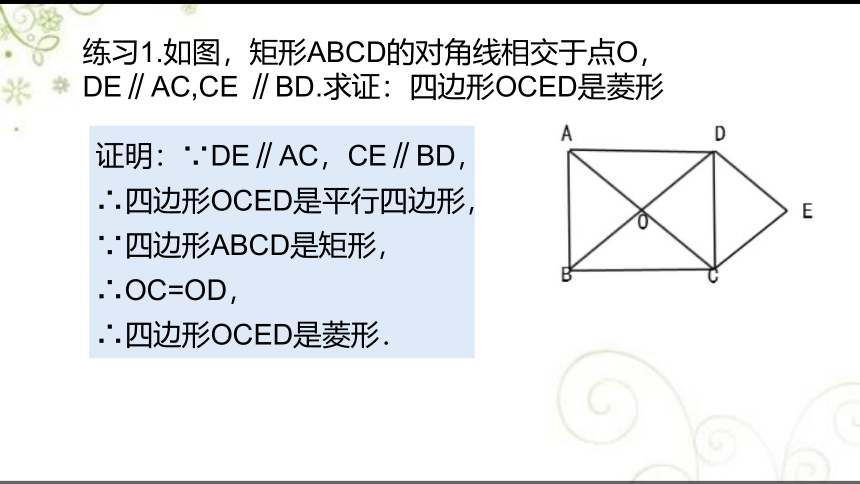
练习1.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE ∥BD.求证:四边形OCED是菱形
证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形, ∵四边形ABCD是矩形,
∴OC=OD,
∴四边形OCED是菱形.
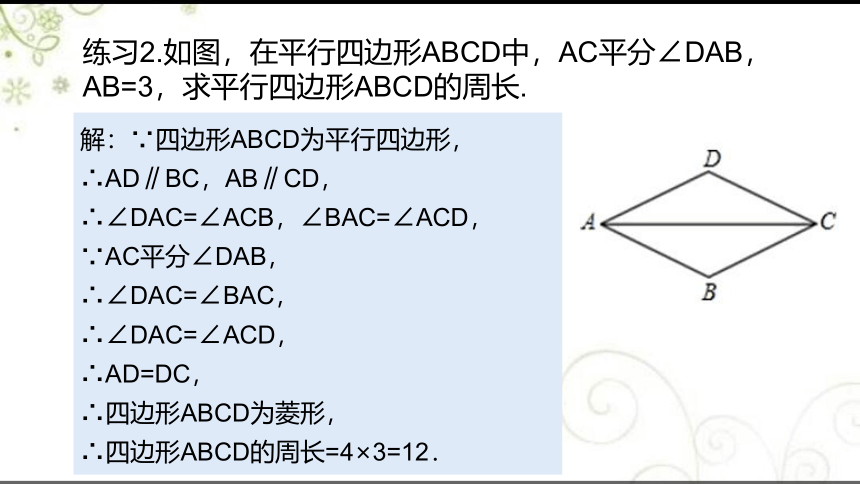
练习2.如图,在平行四边形ABCD中,AC平分∠DAB,AB=3,求平行四边形ABCD的周长.
解:∵四边形ABCD为平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAC=∠ACB,∠BAC=∠ACD,
∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠DAC=∠ACD,
∴AD=DC,
∴四边形ABCD为菱形,
∴四边形ABCD的周长=4×3=12.
我们用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个平行四边形.那么转动木条,这个平行四边形什么时候变成菱形?对此你有什么猜想?
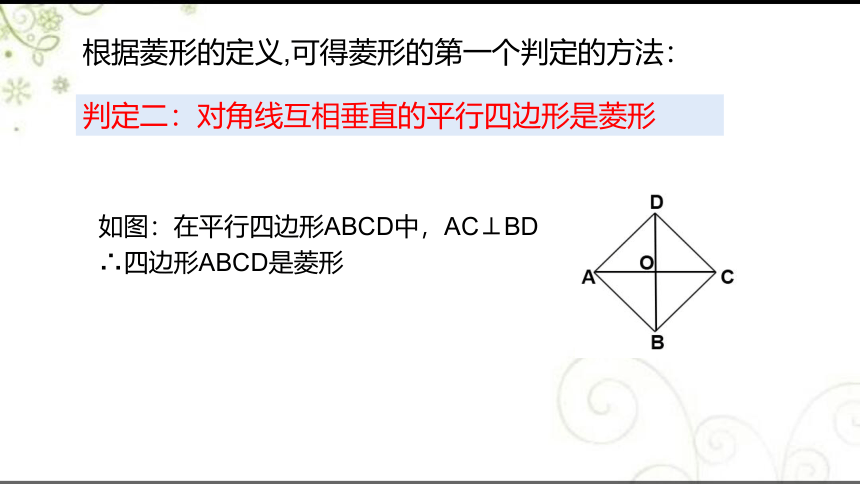
根据菱形的定义,可得菱形的第一个判定的方法:
判定二:对角线互相垂直的平行四边形是菱形
如图:在平行四边形ABCD中,AC⊥BD
∴四边形ABCD是菱形
练习3.如图,四边形ABCD的对角线AC, BD互相垂直,则下列条件能判定四边形ABCD为菱形的条件是( )
A. BA=BC
B. AC,BD互相平分
C. AC=BD
D. AB//CD
B
练习4.如图,在平行四边形ABCD中,点E, F分别是AD, BC上的点,且DE=BF, AC⊥EE求证:四边形AECF是菱形.
解:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
∵DE=BF,
∴AD-DE=BC-BF,
∴AE=FC,
∴AE//FC,
∴四边形AECF为平行四边形,
∵AC⊥EE
∴四边形AECF为菱形.
如图,先画两条等长的线段AB,AD,然后分别以B,D为圆心,AB长为半径画弧,两弧交点为C,连接BC,CD.得到的四边形ABCD是菱形吗?请说明理由.
根据菱形的定义,可得菱形的第一个判定的方法:
判定三:四条边相等的四边形是菱形
如图:在平行四边形ABCD中,AB=BC=CD=DA
∴四边形ABCD是菱形
练习5.如图,AC=8,分别以A, C为圆心,以5为半径作弧,两条弧分别相交于点B, D.依次连接A,B, C, D,连接] BD交AC于点O.判断四边形ABCD的形状,并说明理由;.
解:由题目可知:AB=AD=CB=CD=5
∴四边形ABCD为菱形.
练习6.下列命题:
①四边都相等的四边形是菱形;
②两组邻边分别相等的四边形是菱形;
③对角线互相垂直的平行四边形是菱形;
④对角线相等的四边形是菱形;
⑤一条对角线平分一组对角的平行四边形是菱形.其中正确的是_____________. (填序号)
①③⑤
练习7.下列命题中正确的是 ( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形
C
练习8.如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形ABCD为菱形的是( )
A.AC⊥BD
B. AB=AD
C. AC=BD
D.∠ABD=∠CBD
C
菱形的判定:
1.有一组邻边相等的平行四边形是菱形.
2.对角线互相垂直的平行四边形是菱形.
3.四条边相等的四边形是菱形.
总结
菱形的性质:
1.菱形的四条边都相等,对边平行.
2.菱形的对角都相等.
3.菱形的两条对角线互相垂直平分,并且每一条对角线平分一组对角.
回顾旧识:菱形的定义是什么?性质有哪些?
菱形的定义:有一组邻边相等的平行四边形叫做菱形
根据菱形的定义,可得菱形的第一个判定的方法:
判定一:有一组邻边相等的平行四边形是菱形。
如图:在平行四边形ABCD中,AB=BC
∴四边形ABCD是菱形
练习1.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE ∥BD.求证:四边形OCED是菱形
证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形, ∵四边形ABCD是矩形,
∴OC=OD,
∴四边形OCED是菱形.
练习2.如图,在平行四边形ABCD中,AC平分∠DAB,AB=3,求平行四边形ABCD的周长.
解:∵四边形ABCD为平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAC=∠ACB,∠BAC=∠ACD,
∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠DAC=∠ACD,
∴AD=DC,
∴四边形ABCD为菱形,
∴四边形ABCD的周长=4×3=12.
我们用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个平行四边形.那么转动木条,这个平行四边形什么时候变成菱形?对此你有什么猜想?
根据菱形的定义,可得菱形的第一个判定的方法:
判定二:对角线互相垂直的平行四边形是菱形
如图:在平行四边形ABCD中,AC⊥BD
∴四边形ABCD是菱形
练习3.如图,四边形ABCD的对角线AC, BD互相垂直,则下列条件能判定四边形ABCD为菱形的条件是( )
A. BA=BC
B. AC,BD互相平分
C. AC=BD
D. AB//CD
B
练习4.如图,在平行四边形ABCD中,点E, F分别是AD, BC上的点,且DE=BF, AC⊥EE求证:四边形AECF是菱形.
解:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
∵DE=BF,
∴AD-DE=BC-BF,
∴AE=FC,
∴AE//FC,
∴四边形AECF为平行四边形,
∵AC⊥EE
∴四边形AECF为菱形.
如图,先画两条等长的线段AB,AD,然后分别以B,D为圆心,AB长为半径画弧,两弧交点为C,连接BC,CD.得到的四边形ABCD是菱形吗?请说明理由.
根据菱形的定义,可得菱形的第一个判定的方法:
判定三:四条边相等的四边形是菱形
如图:在平行四边形ABCD中,AB=BC=CD=DA
∴四边形ABCD是菱形
练习5.如图,AC=8,分别以A, C为圆心,以5为半径作弧,两条弧分别相交于点B, D.依次连接A,B, C, D,连接] BD交AC于点O.判断四边形ABCD的形状,并说明理由;.
解:由题目可知:AB=AD=CB=CD=5
∴四边形ABCD为菱形.
练习6.下列命题:
①四边都相等的四边形是菱形;
②两组邻边分别相等的四边形是菱形;
③对角线互相垂直的平行四边形是菱形;
④对角线相等的四边形是菱形;
⑤一条对角线平分一组对角的平行四边形是菱形.其中正确的是_____________. (填序号)
①③⑤
练习7.下列命题中正确的是 ( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形
C
练习8.如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形ABCD为菱形的是( )
A.AC⊥BD
B. AB=AD
C. AC=BD
D.∠ABD=∠CBD
C
菱形的判定:
1.有一组邻边相等的平行四边形是菱形.
2.对角线互相垂直的平行四边形是菱形.
3.四条边相等的四边形是菱形.
总结
