2021年人教版七年级数学上册暑假预习练习(Word版含解答):2.2 整式的加减
文档属性
| 名称 | 2021年人教版七年级数学上册暑假预习练习(Word版含解答):2.2 整式的加减 |  | |
| 格式 | docx | ||
| 文件大小 | 48.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-21 13:29:27 | ||
图片预览




文档简介
2021年人教版七年级数学上册暑假预习练习(Word版含解答):2.2 整式的加减
一、选择题
1.把a﹣2(b﹣c)去括号,正确的一项是(? )
A.?a﹣2b﹣c?????????B.?a﹣2b+c???????????????C.?a﹣2b﹣2c????????????D.?a﹣2b+2c
2.已知 2x6y2 和 -13x3myn 是同类项,则 9m2-5mn-17 的值是(?? )
A.?-1??????????????????????B.?-2??????????????????C.?-3????????????????????D.?-4
3.若 3xm+5y2 与 23x8yn 的差是一个单项式,则代数式 -mn 的值为(? )
A.?-8??????????????????B.?9???????????????????????C.?-9??????????????????????????????D.?-6
4.下列计算正确的是(?? )
A.?3a-a=3???B.?-2m+3m=-5m??????????C.?3x2+2x2=5x4?????D.?2n-5n=-3n
5.已知小明的年龄是 m 岁,爸爸的年龄比小明年龄的 3 倍少 5 岁,妈妈的年龄比小明年龄的 2 倍多 8 岁,则小明爸爸和妈妈的年龄和是(?? )
A.?5m+3????????????????B.?4m-5???????????????C.?5m+7?????????????????D.?6m-3
6.若 (3x2-3x+2)-(-x2+3x-3)=Ax2-Bx+C ,则A,B,C的值分别为(?? )
A.?4,-6,5????????????????????????????B.?4,0,-1????????????????????????????C.?2,0,5????????????????????????????D.?4,6,5
7.如图,两个长方形的面积分别为20,6,两阴影部分的面积分别为a , b , 且 a>b ,则 (a-b) 等于(?? )
A.?6??????????????????B.?7?????????????????????C.?14??????????????????????????D.?16
8.已知:x-3y=4,那么代数式 x-3y-3(y-x)-2(x-3) 的值为(?? )
A.?12???????????????????????B.?13???????????????????????C.?14?????????????????????????D.?16
9.下列等式成立的是(?? )
A.?2÷(12-1)=2÷12-2÷1?????B.?4a4-2a2=2a2??????C.?3a+4b=7ab?????D.?a-b=-(b-a)
10.若代数式 x2+ax+9y-(bx2-x+9y+3) 的值与x的取值无关,则 -a+b 的值为(? )
A.?0????????????????????????B.?﹣1??????????????????????????C.?﹣2????????????????????????D.?2
二、填空题
11.合并同类项: -8x+8x= ________.
12.若长方形的周长为4m , 一边长为 (m-n) ,则其邻边长为________。
13.已知数a、b,c在数轴上的位置如图所示,化简│a+b│-│c-b│的结果是________;
14.若单项式 16x4y2 与 xnym+3 可合并为一项,那么 -n2-m 的值是________.
15.有三堆棋子,数目相等,每堆至少有 5 枚.从左堆中取出 2 枚放入中堆,从右堆中取 4 枚放入中堆,再从中堆中取出与左堆剩余棋子数相同的棋子数放入左堆,这时中堆的棋子数是________.
16.化简: 4(a-b)+(2a-3b)= ________.
17.现规定 |a?bc?d|=a-d+c-b ,则 |xy+2x22xy-x2-3x2-56-xy|= ________.
18.老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如 ﹣2x2﹣2x+1=﹣x2+5x﹣3:则所捂住的多项式是________.
三、解答题
19.化简:(1)xy2-35xy2 ; (2)-15(15a-25b)+12(2a-4b) ;
(3)-[7x-2(4x+2)+2x2]+5x2 .
20.先化简,再求值.
(1)(5a2-3b2)+3(a2-2b2)-2(5a2-2b2) ,其中 a=-1 , b=1 ;
(2)3x-y-[2x-y-3(2xy-x2y)+6xy] ,其中 x=-12 , y=2 .
21.已知实数m使得多项式 (2mx2-x2+3x+1)-(5x2-4y2+3x) 化简后不含 x2 项,求代数式 2m3-[2m3-(4m-5)+m] 的值.
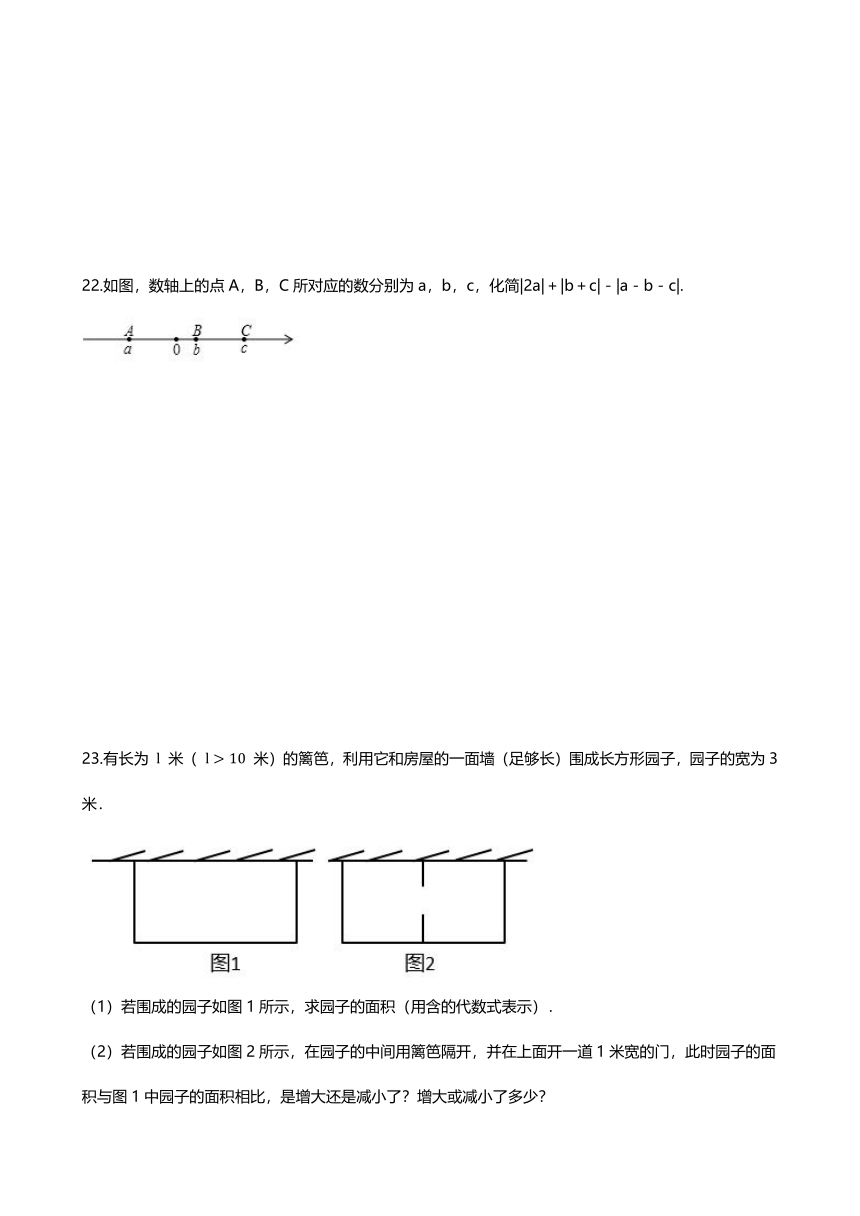
22.如图,数轴上的点A,B,C所对应的数分别为a,b,c,化简|2a|+|b+c|-|a-b-c|.
23.有长为 l 米( l>10 米)的篱笆,利用它和房屋的一面墙(足够长)围成长方形园子,园子的宽为3米.
(1)若围成的园子如图1所示,求园子的面积(用含的代数式表示).
(2)若围成的园子如图2所示,在园子的中间用篱笆隔开,并在上面开一道1米宽的门,此时园子的面积与图1中园子的面积相比,是增大还是减小了?增大或减小了多少?
24.探究活动:
(1)将图①中阴影部分裁剪下来,重新拼成图②一个长方形,则长表示为________,宽为________.
(2)则图②中阴影部分周长表示为________.
(3)知识应用:运用你得到的公式解决以下问题
计算:已知 a=5m-3n , b=3m+5n ,则阴影部分周长是多少?
答案
一、选择题
1.解:a﹣2(b﹣c)= a﹣2b+2c,
故答案为:D.
2.解:由同类项的定义得: {3m=6n=2 ,解得: {m=2n=2
将其代入得: 9m2-5mn-17=9×22-5×2×2-17 =36-20-17 =-1
故答案为:A.
3.解:由 3xm+5y2 与 23x8yn 的差是一个单项式,得
m+5=8,n=2.
解得m=3
∴ -mn=-32=-9
故答案为:C.
4.解:A. 3a-a=2a ,计算错误,不符合题意;
B. -2m+3m=m ,计算错误,不符合题意;
C. 3x2+2x2=5x2 ,计算错误,不符合题意;
D. 2n-5n=-3n ,计算正确,符合题意;
故答案为:D.
5.解:由题意可得,
小明爸爸和妈妈的年龄和是:
(3m-5)+(2m+8)
=3m-5+2m+8
=5m+3(岁),
故答案为:A.
6.解:
∵(3x2-3x+2)-(-x2+3x-3)=3x2-3x+2+x2-3x+3=4x2-6x+5=Ax2-Bx+C
∴A=4 , B=6 , C=5 .
故答案为:D.
7.解:设重叠部分面积为c,
a-b
=(a+c)-(b+c)
=20-6
=14,
故选:C.
8.解: x-3y-3(y-x)-2(x-3)?
=4-3y+3x-2x+6
=10+x-3y
=10+4
=14;
故答案为:C.
9.解:A、 有理数除法没有分配律,故A选项不正确;
B、 4a4-2a2=2a2 ,由 4a4,-2a2 不是同类项,不能合并,故B选项不正确;
C、 3a+4b=7ab ,由 3a,4b 不是同类项,不能合并,故C选项不正确;
D、利用添括号法则知a-b=-(b-a) ,故D选项正确.
故答案为:D.
10.解:由题意得: x2+ax+9y-(bx2-x+9y+3)
= x2+ax+9y-bx2+x-9y-3
= (1-b)x2+(a+1)x-3 ,
∵代数式的值与x的取值无关,
∴ a=-1,b=1 ,
∴ -a+b=2 ;
故答案为:D.
二、填空题
11.解:原式 =0 .
故答案为:0.
12.解: ∵ 长方形的周长为4m , 一边长为 m-n ,
∴ 另一边长为 12×4m-(m-n)=2m-m+n=m+n ,
故答案为:m+n.
13.解:由数轴上点的位置可得:c<b<0<a,且|b|<|a|,
∴a+b>0,c-b<0,
则|a+b|-|c-b|=a+b+c-b=a+c.
故答案为:a+c.
14.解:根据题意得单项式 16x4y2 与 xnym+3 是同类项, ∴n=4,m+3=2 ∴m=-1 ∴-n2-m=-42-(-1)=-16+1=-15
故答案为: -15 .
15.从左堆中取出 2 枚放入中堆,则左堆现在有 (x-2) 枚,中堆现在有 (x+2) 枚;
从右堆中取出 4 枚放入中堆,则右堆现在有 (x-4) 枚,中堆现在有 (x+6) 枚;
从中堆中取出与左堆剩余棋子数相同的棋子数放入左堆,这时中堆的棋子数是 (x+6)-(x-2)=x+6-x+2=8 枚,
故答案为:8.
16.解: 4(a-b)+(2a-3b) =4a-4b+2a-3b =6a-7b .
故答案为:6a-7b.
17.解:∵ |a?bc?d|=a-d+c-b
∴ 原式= xy+2x2-6+xy-3x2-5-2xy+x2
=(xy+xy-2xy)+(2x2-3x2+x2)-11 ?
=-11 ?
故答案为:-11.
18.解:所捂住的多项式是﹣x2+5x﹣3+2x2+2x﹣1=x2+7x﹣4,
故答案为:x2+7x﹣4.
三、解答题
19. (1)原式 =(1-35)xy2 ,
=25xy2 ;
(2)原式 =-15×(15a)+15×(25b)+12×(2a)-12×(4b) ,
=-3a+5b+a-2b ?,
=-2a+3b ;
(3)原式 =-(7x-8x-4+2x2)+5x2 ,
=-7x+8x+4-2x2+5x2 ,
=3x2+x+4 .
20. (1)解:原式 =5a2-3b2+3a2-6b2-10a2+4b2 ,
=-2a2-5b2 ,
将 a=-1 , b=1 代入得:原式 =-2×(-1)2-5×12=-2-5=-7 ;
(2)解:原式 =3x-y-(2x-y-6xy+3x2y+6xy) ,
=3x-y-(2x-y+3x2y) ,
=3x-y-2x+y-3x2y ,
=x-3x2y ,
将 x=-12 , y=2 代入得:原式 =-12-3×(-12)2×2=-12-32=-2 .
21. 解:(2mx2?x2+3x+1)?(5x2?4y2+3x)
=2mx2?x2+3x+1?5x2+4y2?3x
=(2m?6)x2+1+4y2
∵(2mx2?x2+3x+1)?(5x2?4y2+3x)化简后不含x2项,
∴2m?6=0,
解得m=3,
∵ 2m3-[2m3-(4m-5)+m]
= 2m3-(2m3-4m+5+m)
= 2m3-(2m3-3m+5)
= 2m3-2m3+3m-5
= 3m-5 ,
∴当m=3时,原式= 3×3-5=4
22.解:由数轴可知:a<0<b<c,
∴2a<0,b+c>0,a-b-c<0,
∴原式=-2a+(b+c)-(-a+b+c)
=-2a+b+c+a-b-c
=-a.
23. (1)解:由题意得:
图1中园子长为: l-3×2=l-6 (米),
∴图1中园子的面积: 3(l-6)=3l-18 (平方米),
∴园子的面积 (3l-18) 平方米.
(2)解:由题意得:
图2中园子长为: l+1-3×3=l-8 (米),
∴图2中园子的面积: 3(l-8)=3l-24 (平方米),
∴ (3l-18)-(3l-24)=6 (平方米),
∴此时园子的面积比图1中园子的面积减小了6平方米.
24. (1)(a+b);(a-b)
(2)2(a+b+a-b)=4a
(3)解:∵ a=5m-3n , b=3m+5n ,
∴阴影部分周长是4a=20m-12n.
解:(1)由题意可得:
图②长方形的长为:(a+b),宽为:(a-b);
(2)图②中阴影部分周长表示为:2(a+b+a-b)=4a;
一、选择题
1.把a﹣2(b﹣c)去括号,正确的一项是(? )
A.?a﹣2b﹣c?????????B.?a﹣2b+c???????????????C.?a﹣2b﹣2c????????????D.?a﹣2b+2c
2.已知 2x6y2 和 -13x3myn 是同类项,则 9m2-5mn-17 的值是(?? )
A.?-1??????????????????????B.?-2??????????????????C.?-3????????????????????D.?-4
3.若 3xm+5y2 与 23x8yn 的差是一个单项式,则代数式 -mn 的值为(? )
A.?-8??????????????????B.?9???????????????????????C.?-9??????????????????????????????D.?-6
4.下列计算正确的是(?? )
A.?3a-a=3???B.?-2m+3m=-5m??????????C.?3x2+2x2=5x4?????D.?2n-5n=-3n
5.已知小明的年龄是 m 岁,爸爸的年龄比小明年龄的 3 倍少 5 岁,妈妈的年龄比小明年龄的 2 倍多 8 岁,则小明爸爸和妈妈的年龄和是(?? )
A.?5m+3????????????????B.?4m-5???????????????C.?5m+7?????????????????D.?6m-3
6.若 (3x2-3x+2)-(-x2+3x-3)=Ax2-Bx+C ,则A,B,C的值分别为(?? )
A.?4,-6,5????????????????????????????B.?4,0,-1????????????????????????????C.?2,0,5????????????????????????????D.?4,6,5
7.如图,两个长方形的面积分别为20,6,两阴影部分的面积分别为a , b , 且 a>b ,则 (a-b) 等于(?? )
A.?6??????????????????B.?7?????????????????????C.?14??????????????????????????D.?16
8.已知:x-3y=4,那么代数式 x-3y-3(y-x)-2(x-3) 的值为(?? )
A.?12???????????????????????B.?13???????????????????????C.?14?????????????????????????D.?16
9.下列等式成立的是(?? )
A.?2÷(12-1)=2÷12-2÷1?????B.?4a4-2a2=2a2??????C.?3a+4b=7ab?????D.?a-b=-(b-a)
10.若代数式 x2+ax+9y-(bx2-x+9y+3) 的值与x的取值无关,则 -a+b 的值为(? )
A.?0????????????????????????B.?﹣1??????????????????????????C.?﹣2????????????????????????D.?2
二、填空题
11.合并同类项: -8x+8x= ________.
12.若长方形的周长为4m , 一边长为 (m-n) ,则其邻边长为________。
13.已知数a、b,c在数轴上的位置如图所示,化简│a+b│-│c-b│的结果是________;
14.若单项式 16x4y2 与 xnym+3 可合并为一项,那么 -n2-m 的值是________.
15.有三堆棋子,数目相等,每堆至少有 5 枚.从左堆中取出 2 枚放入中堆,从右堆中取 4 枚放入中堆,再从中堆中取出与左堆剩余棋子数相同的棋子数放入左堆,这时中堆的棋子数是________.
16.化简: 4(a-b)+(2a-3b)= ________.
17.现规定 |a?bc?d|=a-d+c-b ,则 |xy+2x22xy-x2-3x2-56-xy|= ________.
18.老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如 ﹣2x2﹣2x+1=﹣x2+5x﹣3:则所捂住的多项式是________.
三、解答题
19.化简:(1)xy2-35xy2 ; (2)-15(15a-25b)+12(2a-4b) ;
(3)-[7x-2(4x+2)+2x2]+5x2 .
20.先化简,再求值.
(1)(5a2-3b2)+3(a2-2b2)-2(5a2-2b2) ,其中 a=-1 , b=1 ;
(2)3x-y-[2x-y-3(2xy-x2y)+6xy] ,其中 x=-12 , y=2 .
21.已知实数m使得多项式 (2mx2-x2+3x+1)-(5x2-4y2+3x) 化简后不含 x2 项,求代数式 2m3-[2m3-(4m-5)+m] 的值.
22.如图,数轴上的点A,B,C所对应的数分别为a,b,c,化简|2a|+|b+c|-|a-b-c|.
23.有长为 l 米( l>10 米)的篱笆,利用它和房屋的一面墙(足够长)围成长方形园子,园子的宽为3米.
(1)若围成的园子如图1所示,求园子的面积(用含的代数式表示).
(2)若围成的园子如图2所示,在园子的中间用篱笆隔开,并在上面开一道1米宽的门,此时园子的面积与图1中园子的面积相比,是增大还是减小了?增大或减小了多少?
24.探究活动:
(1)将图①中阴影部分裁剪下来,重新拼成图②一个长方形,则长表示为________,宽为________.
(2)则图②中阴影部分周长表示为________.
(3)知识应用:运用你得到的公式解决以下问题
计算:已知 a=5m-3n , b=3m+5n ,则阴影部分周长是多少?
答案
一、选择题
1.解:a﹣2(b﹣c)= a﹣2b+2c,
故答案为:D.
2.解:由同类项的定义得: {3m=6n=2 ,解得: {m=2n=2
将其代入得: 9m2-5mn-17=9×22-5×2×2-17 =36-20-17 =-1
故答案为:A.
3.解:由 3xm+5y2 与 23x8yn 的差是一个单项式,得
m+5=8,n=2.
解得m=3
∴ -mn=-32=-9
故答案为:C.
4.解:A. 3a-a=2a ,计算错误,不符合题意;
B. -2m+3m=m ,计算错误,不符合题意;
C. 3x2+2x2=5x2 ,计算错误,不符合题意;
D. 2n-5n=-3n ,计算正确,符合题意;
故答案为:D.
5.解:由题意可得,
小明爸爸和妈妈的年龄和是:
(3m-5)+(2m+8)
=3m-5+2m+8
=5m+3(岁),
故答案为:A.
6.解:
∵(3x2-3x+2)-(-x2+3x-3)=3x2-3x+2+x2-3x+3=4x2-6x+5=Ax2-Bx+C
∴A=4 , B=6 , C=5 .
故答案为:D.
7.解:设重叠部分面积为c,
a-b
=(a+c)-(b+c)
=20-6
=14,
故选:C.
8.解: x-3y-3(y-x)-2(x-3)?
=4-3y+3x-2x+6
=10+x-3y
=10+4
=14;
故答案为:C.
9.解:A、 有理数除法没有分配律,故A选项不正确;
B、 4a4-2a2=2a2 ,由 4a4,-2a2 不是同类项,不能合并,故B选项不正确;
C、 3a+4b=7ab ,由 3a,4b 不是同类项,不能合并,故C选项不正确;
D、利用添括号法则知a-b=-(b-a) ,故D选项正确.
故答案为:D.
10.解:由题意得: x2+ax+9y-(bx2-x+9y+3)
= x2+ax+9y-bx2+x-9y-3
= (1-b)x2+(a+1)x-3 ,
∵代数式的值与x的取值无关,
∴ a=-1,b=1 ,
∴ -a+b=2 ;
故答案为:D.
二、填空题
11.解:原式 =0 .
故答案为:0.
12.解: ∵ 长方形的周长为4m , 一边长为 m-n ,
∴ 另一边长为 12×4m-(m-n)=2m-m+n=m+n ,
故答案为:m+n.
13.解:由数轴上点的位置可得:c<b<0<a,且|b|<|a|,
∴a+b>0,c-b<0,
则|a+b|-|c-b|=a+b+c-b=a+c.
故答案为:a+c.
14.解:根据题意得单项式 16x4y2 与 xnym+3 是同类项, ∴n=4,m+3=2 ∴m=-1 ∴-n2-m=-42-(-1)=-16+1=-15
故答案为: -15 .
15.从左堆中取出 2 枚放入中堆,则左堆现在有 (x-2) 枚,中堆现在有 (x+2) 枚;
从右堆中取出 4 枚放入中堆,则右堆现在有 (x-4) 枚,中堆现在有 (x+6) 枚;
从中堆中取出与左堆剩余棋子数相同的棋子数放入左堆,这时中堆的棋子数是 (x+6)-(x-2)=x+6-x+2=8 枚,
故答案为:8.
16.解: 4(a-b)+(2a-3b) =4a-4b+2a-3b =6a-7b .
故答案为:6a-7b.
17.解:∵ |a?bc?d|=a-d+c-b
∴ 原式= xy+2x2-6+xy-3x2-5-2xy+x2
=(xy+xy-2xy)+(2x2-3x2+x2)-11 ?
=-11 ?
故答案为:-11.
18.解:所捂住的多项式是﹣x2+5x﹣3+2x2+2x﹣1=x2+7x﹣4,
故答案为:x2+7x﹣4.
三、解答题
19. (1)原式 =(1-35)xy2 ,
=25xy2 ;
(2)原式 =-15×(15a)+15×(25b)+12×(2a)-12×(4b) ,
=-3a+5b+a-2b ?,
=-2a+3b ;
(3)原式 =-(7x-8x-4+2x2)+5x2 ,
=-7x+8x+4-2x2+5x2 ,
=3x2+x+4 .
20. (1)解:原式 =5a2-3b2+3a2-6b2-10a2+4b2 ,
=-2a2-5b2 ,
将 a=-1 , b=1 代入得:原式 =-2×(-1)2-5×12=-2-5=-7 ;
(2)解:原式 =3x-y-(2x-y-6xy+3x2y+6xy) ,
=3x-y-(2x-y+3x2y) ,
=3x-y-2x+y-3x2y ,
=x-3x2y ,
将 x=-12 , y=2 代入得:原式 =-12-3×(-12)2×2=-12-32=-2 .
21. 解:(2mx2?x2+3x+1)?(5x2?4y2+3x)
=2mx2?x2+3x+1?5x2+4y2?3x
=(2m?6)x2+1+4y2
∵(2mx2?x2+3x+1)?(5x2?4y2+3x)化简后不含x2项,
∴2m?6=0,
解得m=3,
∵ 2m3-[2m3-(4m-5)+m]
= 2m3-(2m3-4m+5+m)
= 2m3-(2m3-3m+5)
= 2m3-2m3+3m-5
= 3m-5 ,
∴当m=3时,原式= 3×3-5=4
22.解:由数轴可知:a<0<b<c,
∴2a<0,b+c>0,a-b-c<0,
∴原式=-2a+(b+c)-(-a+b+c)
=-2a+b+c+a-b-c
=-a.
23. (1)解:由题意得:
图1中园子长为: l-3×2=l-6 (米),
∴图1中园子的面积: 3(l-6)=3l-18 (平方米),
∴园子的面积 (3l-18) 平方米.
(2)解:由题意得:
图2中园子长为: l+1-3×3=l-8 (米),
∴图2中园子的面积: 3(l-8)=3l-24 (平方米),
∴ (3l-18)-(3l-24)=6 (平方米),
∴此时园子的面积比图1中园子的面积减小了6平方米.
24. (1)(a+b);(a-b)
(2)2(a+b+a-b)=4a
(3)解:∵ a=5m-3n , b=3m+5n ,
∴阴影部分周长是4a=20m-12n.
解:(1)由题意可得:
图②长方形的长为:(a+b),宽为:(a-b);
(2)图②中阴影部分周长表示为:2(a+b+a-b)=4a;
