苏教版五年级数学下册试题 一课一练《解决问题的策略》习题(含答案)
文档属性
| 名称 | 苏教版五年级数学下册试题 一课一练《解决问题的策略》习题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 394.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-22 09:06:57 | ||
图片预览

文档简介
《解决问题的策略》习题
一、选择题
1.下列现象,属于平移的是
A.电风扇的转动
B.分针的转动
C.电梯上下运动
2.如图,阴影部分面积占整个图形面积的
A.
B.
C.
D.
3.圆的半径扩大到原来的3倍,面积扩大到原来的
A.3倍
B.6倍
C.9倍
D.12倍
4.用同样长的铁丝围成一个正方形和一个圆, 的面积大.
A.圆
B.正方形
C.一样大
D.无法判断
5.要剪一个面积是12.56平方厘米的圆形纸片,至少需要面积是 平方厘米的正方形纸片取.
A.12.56
B.14
C.16
D.20
二、填空题
1.如图,阴影部分的面积是
平方分米.
2.一张光盘的刻录面为环形,内圆的直径是4厘米,外圆直径是12厘米,这张光盘刻录面的面积是
平方厘米.
3.图
中的阴影部分面积可用来计算.
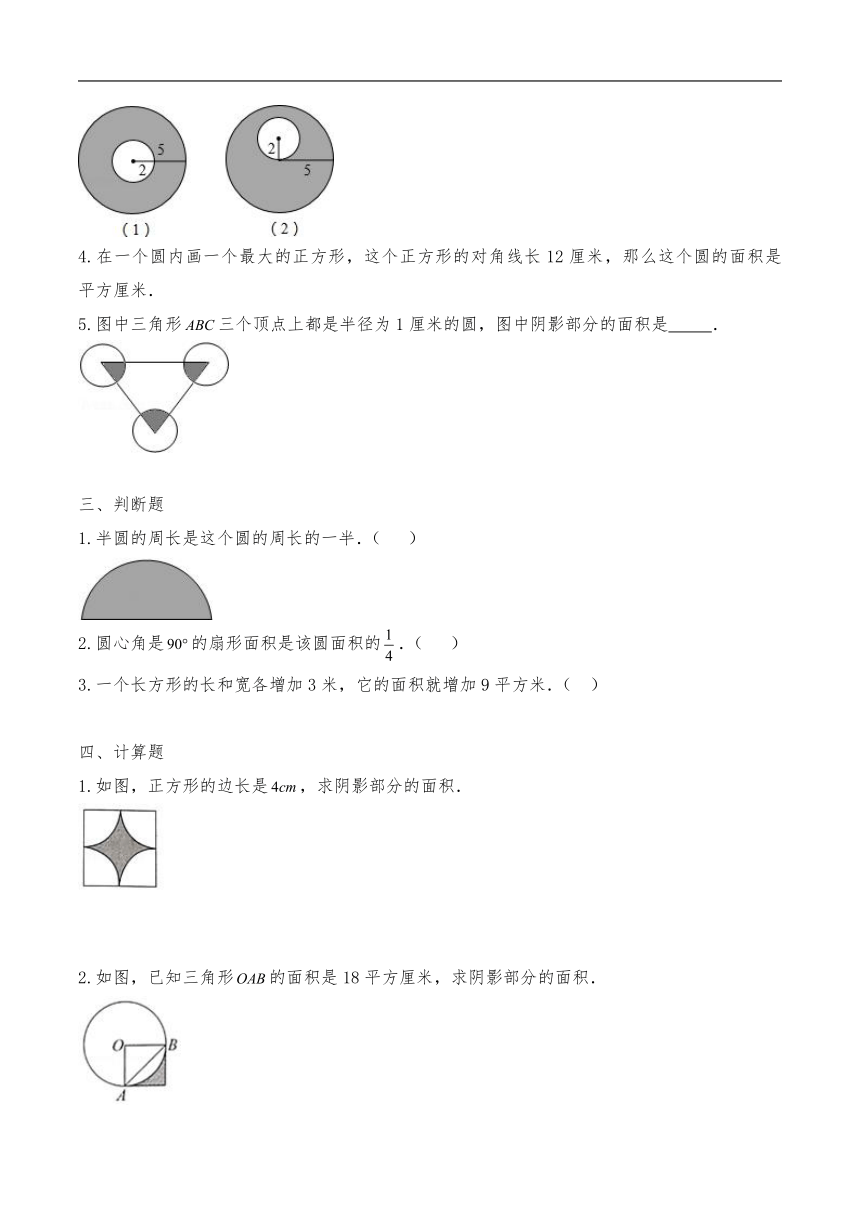
4.在一个圆内画一个最大的正方形,这个正方形的对角线长12厘米,那么这个圆的面积是 平方厘米.
5.图中三角形三个顶点上都是半径为1厘米的圆,图中阴影部分的面积是
.
三、判断题
1.半圆的周长是这个圆的周长的一半.(
)
2.圆心角是的扇形面积是该圆面积的.(
)
3.一个长方形的长和宽各增加3米,它的面积就增加9平方米.(
)
四、计算题
1.如图,正方形的边长是,求阴影部分的面积.
2.如图,已知三角形的面积是18平方厘米,求阴影部分的面积.
3.求如图阴影部分的面积.(单位:
4.如图,计算阴影部分的面积.(单位:厘米)
5.①计算图1阴影部分的周长.
②两个正方形相拼,求图2阴影部分的面积.
6.计算阴影部分的面积.
五、解决问题
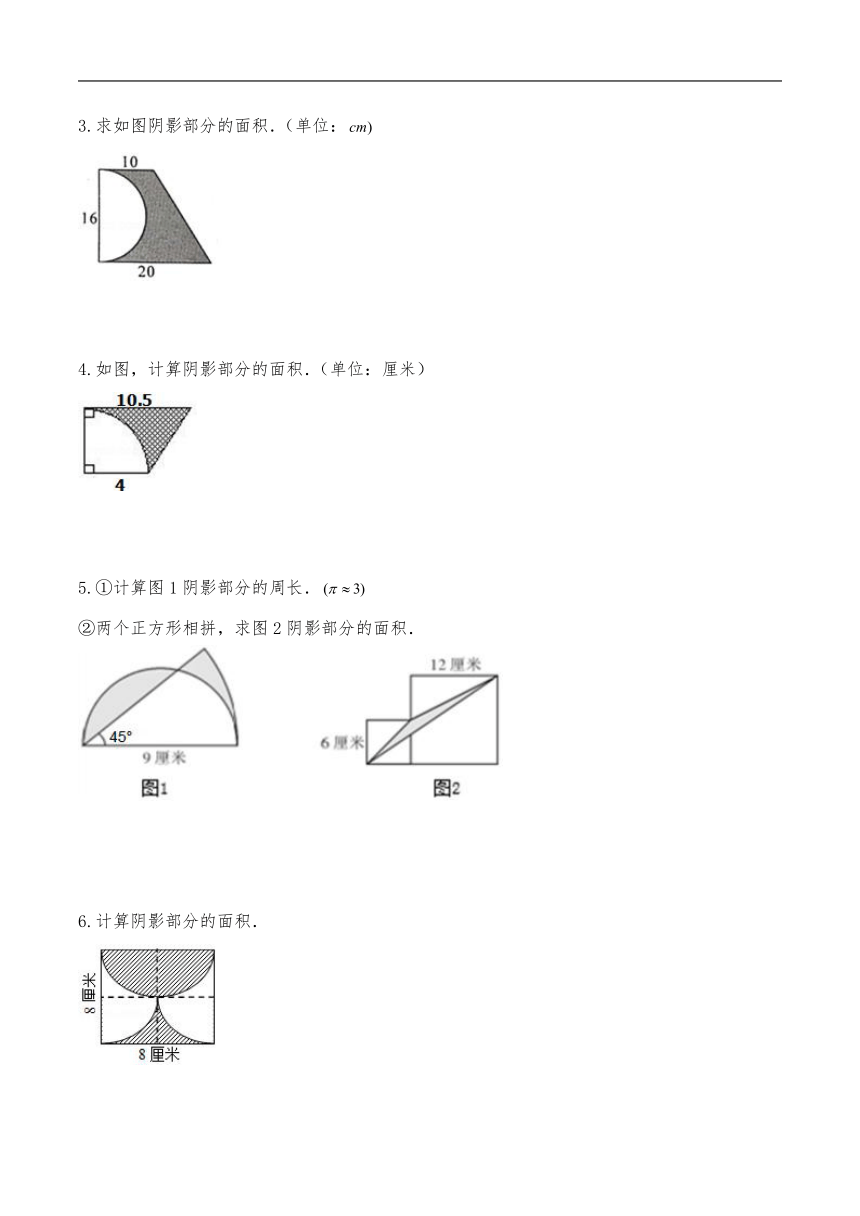
1.如图,王大爷靠墙围了一个半径为的半圆形养鸡场,并在它的外围铺了一条宽的小路,这条小路的面积是多少平方米?取
2.在长方形广场的中间有宽2米的十字形路,其余的地方是草坪,草坪的面积是多少?
3.如图1所示,大小两个正方形并排放在一起,请在图2中用阴影画出一个几何图形(不一定是三角形,可以是任意的多边形),使它的面积等于图1中的阴影面积.
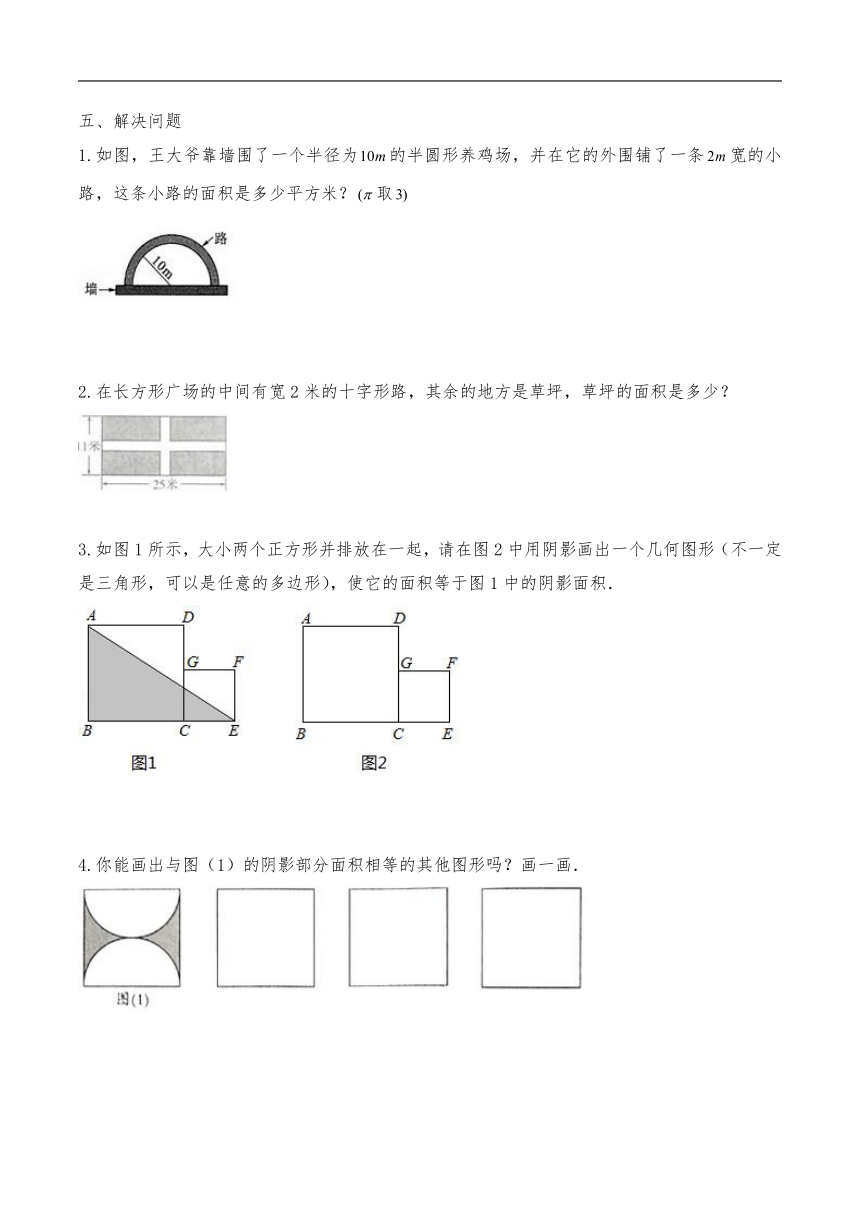
4.你能画出与图(1)的阴影部分面积相等的其他图形吗?画一画.
5.在括号里填上合适的数.
6.看图求出阴影部分的面积?
7.计算图阴影部分的面积(单位:分米)
8.求出图形中阴影部分的面积.(单位:分米,
9.图中,是边长为8厘米的正方形.
(1)三角形的面积是多少?
(2)三角形的面积比三角形的面积大6平方厘米,求阴影部分的面积.
10.计算如图阴影部分的面积:(单位:厘米)
答案
一、选择题
1..2..3..4..5..
二、填空题
1.12.56.
2.100.48.
3.(2).
4.113.04.
5.1.57平方厘米.
三、判断题
1..2..3..
四、计算题
1.解:
(平方厘米)
答:阴影部分的面积是3.44平方厘米.
2.解:设圆的半径是厘米,那么三角形的底、高,正方形的边长都是厘米;
(平方厘米)
(平方厘米)
答:阴影部分的面积是7.74平方厘米.
3.解:
(平方厘米)
答:阴影部分的面积是139.52平方厘米.
4.解:
(平方厘米)
答:阴影部分的面积是16.44平方厘米.
5.解:(1)
(厘米)
答:阴影部分的面积为29.25厘米.
(2)
(平方厘米)
答:阴影部分面积为18平方厘米.
6.解:
(平方厘米)
答:阴影部分的面积是32平方厘米.
五、解决问题
1.解:(米
(平方米)
答:这条小路的面积是66平方米.
2.解:
(平方米)
答:草坪的面积是207平方米.
3.解:如图1所示,大小两个正方形并排放在一起,请在图2中用阴影画出一个几何图形(不一定是三角形,可以是任意的多边形),使它的面积等于图1中的阴影面积(绿色阴影部分).
4.解:如图所示:
5.解:
故答案为:4;4;8;8;12;12;12(答案不唯一).
6.解:,
,
(平方厘米);
答:阴影部分的面积是12.5平方厘米.
7.解:,
,
,
(平方分米),
答:阴影部分的面积是3.86平方分米.
8.解:
(平方分米)
答:阴影部分的面积是77.04平方分米.
9.解:(1)
(平方厘米)
答:三角形的面积是32平方厘米.
(2)设为厘米,得:
(平方厘米)
答:阴影部分的面积是38平方厘米.
10.解:(厘米)
(平方厘米)
答:阴影部分的面积为11.44平方厘米.
一、选择题
1.下列现象,属于平移的是
A.电风扇的转动
B.分针的转动
C.电梯上下运动
2.如图,阴影部分面积占整个图形面积的
A.
B.
C.
D.
3.圆的半径扩大到原来的3倍,面积扩大到原来的
A.3倍
B.6倍
C.9倍
D.12倍
4.用同样长的铁丝围成一个正方形和一个圆, 的面积大.
A.圆
B.正方形
C.一样大
D.无法判断
5.要剪一个面积是12.56平方厘米的圆形纸片,至少需要面积是 平方厘米的正方形纸片取.
A.12.56
B.14
C.16
D.20
二、填空题
1.如图,阴影部分的面积是
平方分米.
2.一张光盘的刻录面为环形,内圆的直径是4厘米,外圆直径是12厘米,这张光盘刻录面的面积是
平方厘米.
3.图
中的阴影部分面积可用来计算.
4.在一个圆内画一个最大的正方形,这个正方形的对角线长12厘米,那么这个圆的面积是 平方厘米.
5.图中三角形三个顶点上都是半径为1厘米的圆,图中阴影部分的面积是
.
三、判断题
1.半圆的周长是这个圆的周长的一半.(
)
2.圆心角是的扇形面积是该圆面积的.(
)
3.一个长方形的长和宽各增加3米,它的面积就增加9平方米.(
)
四、计算题
1.如图,正方形的边长是,求阴影部分的面积.
2.如图,已知三角形的面积是18平方厘米,求阴影部分的面积.
3.求如图阴影部分的面积.(单位:
4.如图,计算阴影部分的面积.(单位:厘米)
5.①计算图1阴影部分的周长.
②两个正方形相拼,求图2阴影部分的面积.
6.计算阴影部分的面积.
五、解决问题
1.如图,王大爷靠墙围了一个半径为的半圆形养鸡场,并在它的外围铺了一条宽的小路,这条小路的面积是多少平方米?取
2.在长方形广场的中间有宽2米的十字形路,其余的地方是草坪,草坪的面积是多少?
3.如图1所示,大小两个正方形并排放在一起,请在图2中用阴影画出一个几何图形(不一定是三角形,可以是任意的多边形),使它的面积等于图1中的阴影面积.
4.你能画出与图(1)的阴影部分面积相等的其他图形吗?画一画.
5.在括号里填上合适的数.
6.看图求出阴影部分的面积?
7.计算图阴影部分的面积(单位:分米)
8.求出图形中阴影部分的面积.(单位:分米,
9.图中,是边长为8厘米的正方形.
(1)三角形的面积是多少?
(2)三角形的面积比三角形的面积大6平方厘米,求阴影部分的面积.
10.计算如图阴影部分的面积:(单位:厘米)
答案
一、选择题
1..2..3..4..5..
二、填空题
1.12.56.
2.100.48.
3.(2).
4.113.04.
5.1.57平方厘米.
三、判断题
1..2..3..
四、计算题
1.解:
(平方厘米)
答:阴影部分的面积是3.44平方厘米.
2.解:设圆的半径是厘米,那么三角形的底、高,正方形的边长都是厘米;
(平方厘米)
(平方厘米)
答:阴影部分的面积是7.74平方厘米.
3.解:
(平方厘米)
答:阴影部分的面积是139.52平方厘米.
4.解:
(平方厘米)
答:阴影部分的面积是16.44平方厘米.
5.解:(1)
(厘米)
答:阴影部分的面积为29.25厘米.
(2)
(平方厘米)
答:阴影部分面积为18平方厘米.
6.解:
(平方厘米)
答:阴影部分的面积是32平方厘米.
五、解决问题
1.解:(米
(平方米)
答:这条小路的面积是66平方米.
2.解:
(平方米)
答:草坪的面积是207平方米.
3.解:如图1所示,大小两个正方形并排放在一起,请在图2中用阴影画出一个几何图形(不一定是三角形,可以是任意的多边形),使它的面积等于图1中的阴影面积(绿色阴影部分).
4.解:如图所示:
5.解:
故答案为:4;4;8;8;12;12;12(答案不唯一).
6.解:,
,
(平方厘米);
答:阴影部分的面积是12.5平方厘米.
7.解:,
,
,
(平方分米),
答:阴影部分的面积是3.86平方分米.
8.解:
(平方分米)
答:阴影部分的面积是77.04平方分米.
9.解:(1)
(平方厘米)
答:三角形的面积是32平方厘米.
(2)设为厘米,得:
(平方厘米)
答:阴影部分的面积是38平方厘米.
10.解:(厘米)
(平方厘米)
答:阴影部分的面积为11.44平方厘米.
