1.5有理数的加法课件- 冀教版数学七年级上册(24张)
文档属性
| 名称 | 1.5有理数的加法课件- 冀教版数学七年级上册(24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 762.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-21 16:40:05 | ||
图片预览






文档简介
(共24张PPT)
1.5
有理数的加法
第1课时
有理数的加法法则
学习目标
1.了解有理数加法的意义;
2.初步掌握有理数的加法法则;(重点)
3.能准确地进行有理数加法运算,并能运用其解决简单的实际问题.(难点)
我是火炬手
演示1
+1
-1
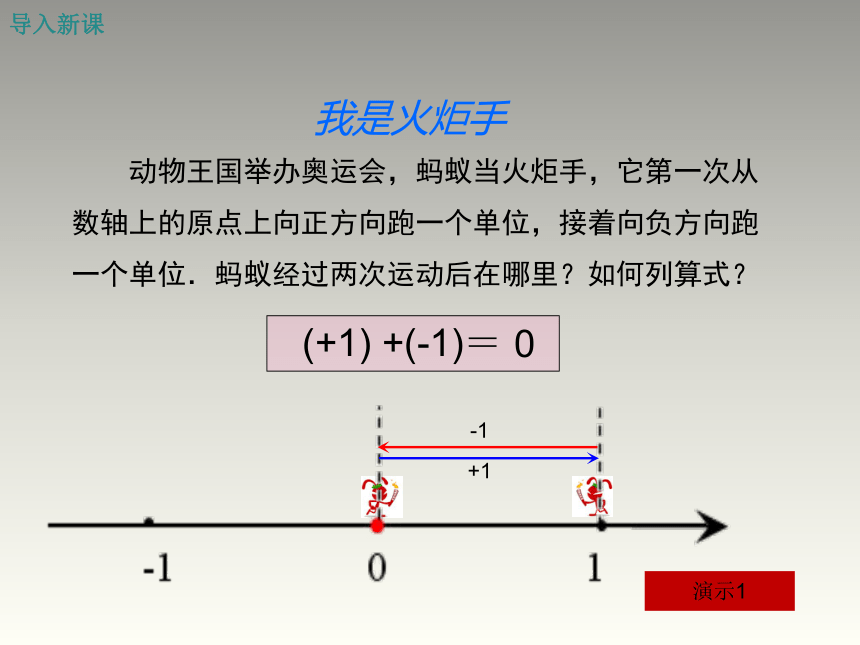
(+1)
+(-1)=
0
动物王国举办奥运会,蚂蚁当火炬手,它第一次从数轴上的原点上向正方向跑一个单位,接着向负方向跑一个单位.蚂蚁经过两次运动后在哪里?如何列算式?
导入新课
讲授新课
有理数的加法法则
一
一只可爱的小狗,在一条东西走向的笔直公路上行走,现规定向东为正,向西为负.
0
1
2
3
4
-1
-2
-3
东
如果小狗先向东行走2米,再继续向东行走1米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
-3
东
解:小狗一共向东行走了(2+1)米,写成算是为:
(+2)+(+1)=
+(2+1)(米)
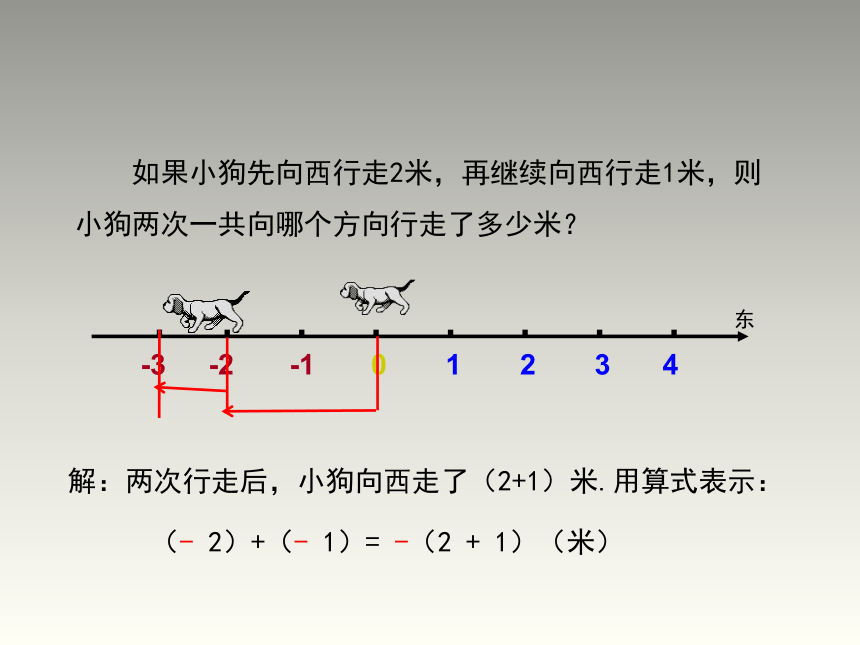
如果小狗先向西行走2米,再继续向西行走1米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
-3
东
解:两次行走后,小狗向西走了(2+1)米.用算式表示:
(-
2)+(-
1)=
-(2
+
1)(米)
(+2)+(+1)=
+(2+1)=+3
(-2)+(-1)=
-(2+1)=-3
加数
加数
和
你从上面两个式子中发现了什么?
同号两数相加,取相同的符号,并把绝对值相加.
有理数加法法则一:
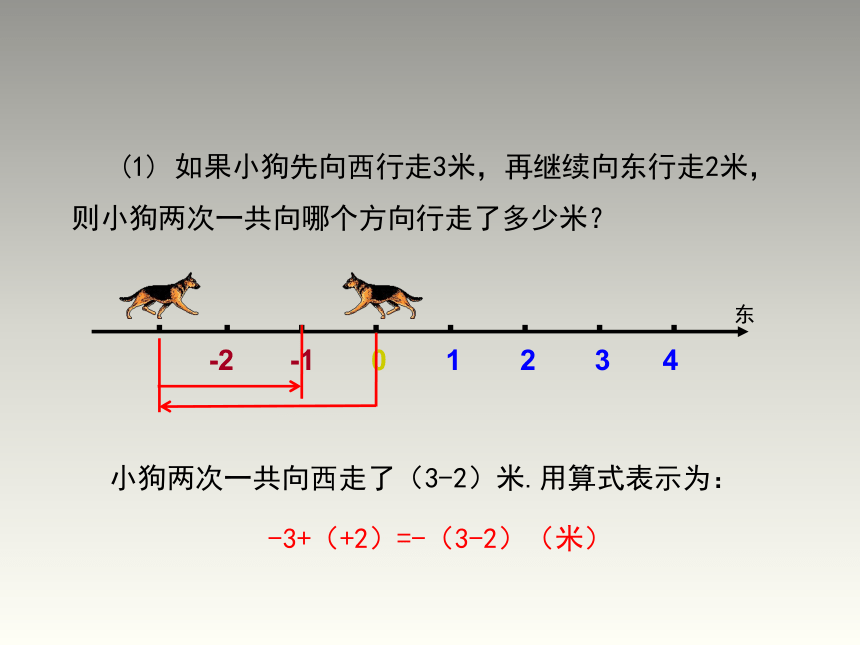
(1)
如果小狗先向西行走3米,再继续向东行走2米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
东
小狗两次一共向西走了(3-2)米.用算式表示为:
-3+(+2)=-(3-2)(米)
(2)
如果小狗先向西行走2米,再继续向东行走3米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
东
小狗两次一共向东走了(3-2)米.用算式表示为:
-2+(+3)=+(3-2)(米)
(3)
如果小狗先向西行走2米,再继续向东行走2米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
东
解:小狗一共行走了0米.写成算式为:
(-2)+(+2)=
0(米)
-2
+
(+3)
=
+(3-2)
-3
+
(+2)=
-(3-2)
-2
+
(+2)=
(2-2)
加数
加数
和
加数异号
加数的绝对值不相等
加数绝对值相等
你从上面三个式子中发现了什么?
有理数加法法则二:
异号两数相加,绝对值相等时和为0;绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
如果小狗先向西行走3米,然后在原地休息,则小狗向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
东
小狗向西行走了3米.写成算式为:
(-3)+0=
-3(米)
有理数加法法则三:
一个数同0相加,仍得这个数.
例1
计算:
(1)(+8)+(+5);(2)(+2.5)+(-2.5);
(3)
+(
);
(4)
(
)+(
)
.
(1)(+8)+(+5)
=+(8+5)
=+13.
同号两数相加,取相同的符号,并把绝对值相加.
异号两数相加,绝对值相等时和为0.
解:
(2)(+2.5)+(-2.5)
=0.
异号两数相加,绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
同号两数相加,取相同的符号,并把绝对值相加.
(3)
(4)
(1)对于有理数的加法法则,关键是抓住“符号”与求“绝对值的和(差)”.
“符号”——同号相加取“相同的符号”,异号相加取“绝对值较大的加数的符号”.
“绝对值的和(差)”——同号做加法,异号做减法,即大数减去小数(较大的绝对值减去较小的绝对值).
(2)一个有理数由符号和绝对值两部分组成,在进行加法运算时,首先要确定和的符号,然后再求绝对值.
例2
海平面的高度为0m.一艘潜艇从海平面先下潜40m,再上升15m.求现在这艘潜艇相对于海平面的位置.(上升为正,下潜为负)
有理数加法的实际应用
二
-50m
-40m
-30m
-20m
-10m
0m
海平面
解:潜水艇下潜40m,记作-40m;上升15m,记作+15m.根据题意,得
(-40)+(+15)
=-(40-25)=-25(m)
答:现在这艘潜艇位于海平面下25米处.
在解与有理数加法有关的实际应用问题时,先利用正负数表示实际问题中的量,再列式计算.
红队
黄队
蓝队
净胜球
红队
4:1
0:1
2
黄队
1:4
1:0
-2
蓝队
1:0
0:1
0
足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
分析:
解:每个队的进球总数记为正数,失球总数记为负数,
这两数的和为这队的净胜球数.
三场比赛中,红队共进4球,失2球,净胜球数为
(+4)+(-2)=+(4-2)=2.
黄队共进2球,失4球,净胜球为
(+2)+(-4)=-(4-2)=-2.
篮球共进1球,失1球,净胜球数为
(+1)+(-1)=0.
.
(1)(-0.6)+(-2.7);
?
(2)3.7+(-8.4);?
(3)(-0.6)+3;
(4)3.22+1.78;
(5)7+(-3.3);??
(6)(-1.9)+(-0.11);
(7)(-9.18)+6.18;
(8)4.2+(-6.7).
当堂练习
1.计算
答案:(1)-3.3;
(2)-4.7;
(3)2.4;
(4)5;
(5)3.7;
(6)-2.01;
(7)-3;
(8)-2.5.
2.用“>”或“<”号填空:
(1)如果a>0,b>0,那么a+b
0;
(2)如果a<0,b<0,那么a+b
0;
(3)如果a>0,b<0,|a|>|b|,那么a+b
0;
(4)如果a<0,b>0,|a|>|b|,那么a+b
0.
3.分别根据下列条件,利用|a|与|b|表示a与b的和:
(1)a>0,b>0;??????
(2)
a<0,b<0;
(3)a>0,b<0,|a|>|b|;????
(4)a>0,b<0,|a|<|b|.
>
>
>
>
4.
一只小虫从某点O出发在一条直线上爬行,规定向右爬行为正,向左爬行为负.小虫共爬行5次,小虫爬行的路程依次记为(单位:厘米):-5,-3,+10,-4,+8.
(1)小虫最后的位置在哪里?
(2)若小虫的爬行速度保持不变,共用了6分钟,则小虫的爬行速度是多少?
解:(1)(-5)+(-3)+(+10)+(-4)+(+8)
=-8+(+10)+(-4)+(+8)
=+2+(-4)+(+8)
=-2+(+8)
=6(厘米).
(2)|-5|+|-3|+|+10|+|-4|+|+8|
=5+3+10+4+8
=30(厘米),
30÷6=5(厘米/分).
答:小虫最后在离出发点右侧6厘米处.小虫的爬行速度
为5厘米/分.
课堂小结
确定类型
定符号
绝对值
同号
异号(绝对值不相等)
异号(绝对值相等)
与0相加
相同符号
取绝对值较大的加数的符号
相加
相减
结果是0
仍是这个数
有理数的加法法则:
1.5
有理数的加法
第1课时
有理数的加法法则
学习目标
1.了解有理数加法的意义;
2.初步掌握有理数的加法法则;(重点)
3.能准确地进行有理数加法运算,并能运用其解决简单的实际问题.(难点)
我是火炬手
演示1
+1
-1
(+1)
+(-1)=
0
动物王国举办奥运会,蚂蚁当火炬手,它第一次从数轴上的原点上向正方向跑一个单位,接着向负方向跑一个单位.蚂蚁经过两次运动后在哪里?如何列算式?
导入新课
讲授新课
有理数的加法法则
一
一只可爱的小狗,在一条东西走向的笔直公路上行走,现规定向东为正,向西为负.
0
1
2
3
4
-1
-2
-3
东
如果小狗先向东行走2米,再继续向东行走1米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
-3
东
解:小狗一共向东行走了(2+1)米,写成算是为:
(+2)+(+1)=
+(2+1)(米)
如果小狗先向西行走2米,再继续向西行走1米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
-3
东
解:两次行走后,小狗向西走了(2+1)米.用算式表示:
(-
2)+(-
1)=
-(2
+
1)(米)
(+2)+(+1)=
+(2+1)=+3
(-2)+(-1)=
-(2+1)=-3
加数
加数
和
你从上面两个式子中发现了什么?
同号两数相加,取相同的符号,并把绝对值相加.
有理数加法法则一:
(1)
如果小狗先向西行走3米,再继续向东行走2米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
东
小狗两次一共向西走了(3-2)米.用算式表示为:
-3+(+2)=-(3-2)(米)
(2)
如果小狗先向西行走2米,再继续向东行走3米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
东
小狗两次一共向东走了(3-2)米.用算式表示为:
-2+(+3)=+(3-2)(米)
(3)
如果小狗先向西行走2米,再继续向东行走2米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
东
解:小狗一共行走了0米.写成算式为:
(-2)+(+2)=
0(米)
-2
+
(+3)
=
+(3-2)
-3
+
(+2)=
-(3-2)
-2
+
(+2)=
(2-2)
加数
加数
和
加数异号
加数的绝对值不相等
加数绝对值相等
你从上面三个式子中发现了什么?
有理数加法法则二:
异号两数相加,绝对值相等时和为0;绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
如果小狗先向西行走3米,然后在原地休息,则小狗向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
东
小狗向西行走了3米.写成算式为:
(-3)+0=
-3(米)
有理数加法法则三:
一个数同0相加,仍得这个数.
例1
计算:
(1)(+8)+(+5);(2)(+2.5)+(-2.5);
(3)
+(
);
(4)
(
)+(
)
.
(1)(+8)+(+5)
=+(8+5)
=+13.
同号两数相加,取相同的符号,并把绝对值相加.
异号两数相加,绝对值相等时和为0.
解:
(2)(+2.5)+(-2.5)
=0.
异号两数相加,绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
同号两数相加,取相同的符号,并把绝对值相加.
(3)
(4)
(1)对于有理数的加法法则,关键是抓住“符号”与求“绝对值的和(差)”.
“符号”——同号相加取“相同的符号”,异号相加取“绝对值较大的加数的符号”.
“绝对值的和(差)”——同号做加法,异号做减法,即大数减去小数(较大的绝对值减去较小的绝对值).
(2)一个有理数由符号和绝对值两部分组成,在进行加法运算时,首先要确定和的符号,然后再求绝对值.
例2
海平面的高度为0m.一艘潜艇从海平面先下潜40m,再上升15m.求现在这艘潜艇相对于海平面的位置.(上升为正,下潜为负)
有理数加法的实际应用
二
-50m
-40m
-30m
-20m
-10m
0m
海平面
解:潜水艇下潜40m,记作-40m;上升15m,记作+15m.根据题意,得
(-40)+(+15)
=-(40-25)=-25(m)
答:现在这艘潜艇位于海平面下25米处.
在解与有理数加法有关的实际应用问题时,先利用正负数表示实际问题中的量,再列式计算.
红队
黄队
蓝队
净胜球
红队
4:1
0:1
2
黄队
1:4
1:0
-2
蓝队
1:0
0:1
0
足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
分析:
解:每个队的进球总数记为正数,失球总数记为负数,
这两数的和为这队的净胜球数.
三场比赛中,红队共进4球,失2球,净胜球数为
(+4)+(-2)=+(4-2)=2.
黄队共进2球,失4球,净胜球为
(+2)+(-4)=-(4-2)=-2.
篮球共进1球,失1球,净胜球数为
(+1)+(-1)=0.
.
(1)(-0.6)+(-2.7);
?
(2)3.7+(-8.4);?
(3)(-0.6)+3;
(4)3.22+1.78;
(5)7+(-3.3);??
(6)(-1.9)+(-0.11);
(7)(-9.18)+6.18;
(8)4.2+(-6.7).
当堂练习
1.计算
答案:(1)-3.3;
(2)-4.7;
(3)2.4;
(4)5;
(5)3.7;
(6)-2.01;
(7)-3;
(8)-2.5.
2.用“>”或“<”号填空:
(1)如果a>0,b>0,那么a+b
0;
(2)如果a<0,b<0,那么a+b
0;
(3)如果a>0,b<0,|a|>|b|,那么a+b
0;
(4)如果a<0,b>0,|a|>|b|,那么a+b
0.
3.分别根据下列条件,利用|a|与|b|表示a与b的和:
(1)a>0,b>0;??????
(2)
a<0,b<0;
(3)a>0,b<0,|a|>|b|;????
(4)a>0,b<0,|a|<|b|.
>
>
>
>
4.
一只小虫从某点O出发在一条直线上爬行,规定向右爬行为正,向左爬行为负.小虫共爬行5次,小虫爬行的路程依次记为(单位:厘米):-5,-3,+10,-4,+8.
(1)小虫最后的位置在哪里?
(2)若小虫的爬行速度保持不变,共用了6分钟,则小虫的爬行速度是多少?
解:(1)(-5)+(-3)+(+10)+(-4)+(+8)
=-8+(+10)+(-4)+(+8)
=+2+(-4)+(+8)
=-2+(+8)
=6(厘米).
(2)|-5|+|-3|+|+10|+|-4|+|+8|
=5+3+10+4+8
=30(厘米),
30÷6=5(厘米/分).
答:小虫最后在离出发点右侧6厘米处.小虫的爬行速度
为5厘米/分.
课堂小结
确定类型
定符号
绝对值
同号
异号(绝对值不相等)
异号(绝对值相等)
与0相加
相同符号
取绝对值较大的加数的符号
相加
相减
结果是0
仍是这个数
有理数的加法法则:
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
