1.9有理数的除法说课课件- 冀教版数学七年级上册(28张)
文档属性
| 名称 | 1.9有理数的除法说课课件- 冀教版数学七年级上册(28张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-21 16:37:46 | ||
图片预览






文档简介
(共28张PPT)
1.9有理数的除法
教材分析
一
学情分析
二
教法选择与学法指导
三
教学过程
四
板书设计
五
说课内容
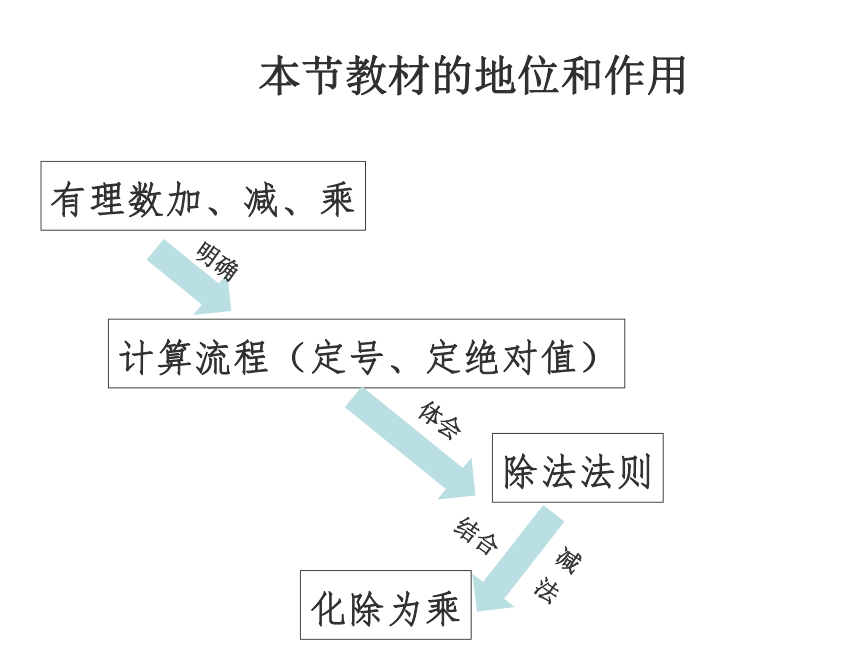
有理数加、减、乘
计算流程(定号、定绝对值)
除法法则
明确
化除为乘
本节教材的地位和作用
体会
结合
减法
学习目标
1、经历有理数除法法则的形成过程的推导;
2、掌握并运用有理数除法法则进行有理数的除法计算.
教学重点和难点
重点:1.探究有理数的除法法则;
2.掌握有理数除法法则并进行计算.
难点:有理数法则的形成过程.
学情分析
1.熟知乘法与除法互为逆运算,而且也熟悉“除一个数等于乘以它的倒数的运算”的法则;
2.对负数参与运算有了一定认识;
3.能够初步开展小组活动
4.学生善于表现,能够积极参与课堂
教法选择与学法指导
教学模式:数学交流
实际
问题
思考
交流
总结
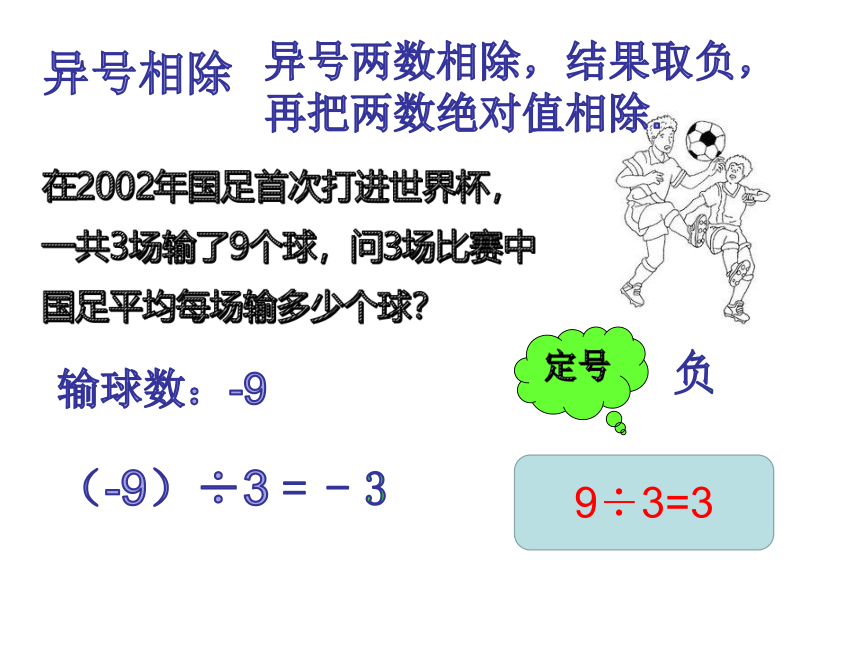
9÷3=3
计算:
(1)
(-18)
÷6
(2)
63÷(-7)
(3)
1
÷(-9)
(4)(-12)÷2
这一周经营情况如何?
别提了,一周就赔了700元.
8÷2=4
12÷3=4
两个负数相除
两个负数相乘
负负得正
计算:
(1)
(-12)
÷(-6)
(2)
(-63)÷(-7)
(3)
(-100)÷(-10)
(4)
(-12)÷(-2)
(5)
(+24)÷(+4)
(6)
(-2)÷2
两个有理数相除,
同号得____,
异号得_____,并把绝对值_______.
正
负
相除
0不能作为除数
0除以任何一个
不等于0
的数都得_____.
0
两种运算定号方式一样哟!
﹣
﹣
+
+
练一练
计算:
(-14)÷7=___
-2
8÷
(-4)=___
-2
-2
-2
合作探究
-6÷(-3)=
除法
乘法
转化
互为倒数
相同的结果
-3
-6×(-
)=
1
3
1
3
-
+2
+2
这样,有理数的除法都能转化为乘法!
注意:零不能作除数
除以一个数等于乘上这个数的倒数.
对比记忆
有理数的减法法则
减去一个数,等于加这个数的相反数.
a
-
b
=
a
+
(-b)
减数变为相反数作加数
减号变加号
有理数的除法法则
除以一个不等于0的数,等于乘这个数的倒数.
a
÷
b
=
a
·
(b≠0)
除号变乘号
除数变为倒数作因数
(1)(-18)÷(-6)
=3
解法二:
解:原式=+(
)
=3
=-3
=
-
3
解:原式=(-18)×(
)
(2)(
)÷(+
)
(3)
÷(
)
解:原式=
×(
)
=
解:原式=(
)×(+5)
解:原式=-(
)
=
-
(
×5
)
解:原式=
-
(
÷
)
=
-(
×
)
=
18÷6
÷
一般地:当除数为整数时一般用除法法则一,当除数为分数时一般化除为乘.
化除为乘
直接定号、定绝对值
运算中遇到小数和分数时,处理的方法与小学一样,小数化成分数,带分数化成假分数,然后相除.
你发现什么了?
解:
解:
乘除混合运算要选
“化乘为除”!
方法一
除以一个数(不等于0)等于乘这个数的倒数
异号相除
同号相除
并把绝对值相除
方法二
化除
为乘
特别提醒:0除以任何不等于0的数都得0.
课后探索乐园
设a,b,c为非零有理数,求下列式子的值.
有理数的除法
1.9有理数的除法
教材分析
一
学情分析
二
教法选择与学法指导
三
教学过程
四
板书设计
五
说课内容
有理数加、减、乘
计算流程(定号、定绝对值)
除法法则
明确
化除为乘
本节教材的地位和作用
体会
结合
减法
学习目标
1、经历有理数除法法则的形成过程的推导;
2、掌握并运用有理数除法法则进行有理数的除法计算.
教学重点和难点
重点:1.探究有理数的除法法则;
2.掌握有理数除法法则并进行计算.
难点:有理数法则的形成过程.
学情分析
1.熟知乘法与除法互为逆运算,而且也熟悉“除一个数等于乘以它的倒数的运算”的法则;
2.对负数参与运算有了一定认识;
3.能够初步开展小组活动
4.学生善于表现,能够积极参与课堂
教法选择与学法指导
教学模式:数学交流
实际
问题
思考
交流
总结
9÷3=3
计算:
(1)
(-18)
÷6
(2)
63÷(-7)
(3)
1
÷(-9)
(4)(-12)÷2
这一周经营情况如何?
别提了,一周就赔了700元.
8÷2=4
12÷3=4
两个负数相除
两个负数相乘
负负得正
计算:
(1)
(-12)
÷(-6)
(2)
(-63)÷(-7)
(3)
(-100)÷(-10)
(4)
(-12)÷(-2)
(5)
(+24)÷(+4)
(6)
(-2)÷2
两个有理数相除,
同号得____,
异号得_____,并把绝对值_______.
正
负
相除
0不能作为除数
0除以任何一个
不等于0
的数都得_____.
0
两种运算定号方式一样哟!
﹣
﹣
+
+
练一练
计算:
(-14)÷7=___
-2
8÷
(-4)=___
-2
-2
-2
合作探究
-6÷(-3)=
除法
乘法
转化
互为倒数
相同的结果
-3
-6×(-
)=
1
3
1
3
-
+2
+2
这样,有理数的除法都能转化为乘法!
注意:零不能作除数
除以一个数等于乘上这个数的倒数.
对比记忆
有理数的减法法则
减去一个数,等于加这个数的相反数.
a
-
b
=
a
+
(-b)
减数变为相反数作加数
减号变加号
有理数的除法法则
除以一个不等于0的数,等于乘这个数的倒数.
a
÷
b
=
a
·
(b≠0)
除号变乘号
除数变为倒数作因数
(1)(-18)÷(-6)
=3
解法二:
解:原式=+(
)
=3
=-3
=
-
3
解:原式=(-18)×(
)
(2)(
)÷(+
)
(3)
÷(
)
解:原式=
×(
)
=
解:原式=(
)×(+5)
解:原式=-(
)
=
-
(
×5
)
解:原式=
-
(
÷
)
=
-(
×
)
=
18÷6
÷
一般地:当除数为整数时一般用除法法则一,当除数为分数时一般化除为乘.
化除为乘
直接定号、定绝对值
运算中遇到小数和分数时,处理的方法与小学一样,小数化成分数,带分数化成假分数,然后相除.
你发现什么了?
解:
解:
乘除混合运算要选
“化乘为除”!
方法一
除以一个数(不等于0)等于乘这个数的倒数
异号相除
同号相除
并把绝对值相除
方法二
化除
为乘
特别提醒:0除以任何不等于0的数都得0.
课后探索乐园
设a,b,c为非零有理数,求下列式子的值.
有理数的除法
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
