2021年湘教版数学九年级下第1章二次函数能力提升训练(word版含答案)
文档属性
| 名称 | 2021年湘教版数学九年级下第1章二次函数能力提升训练(word版含答案) | 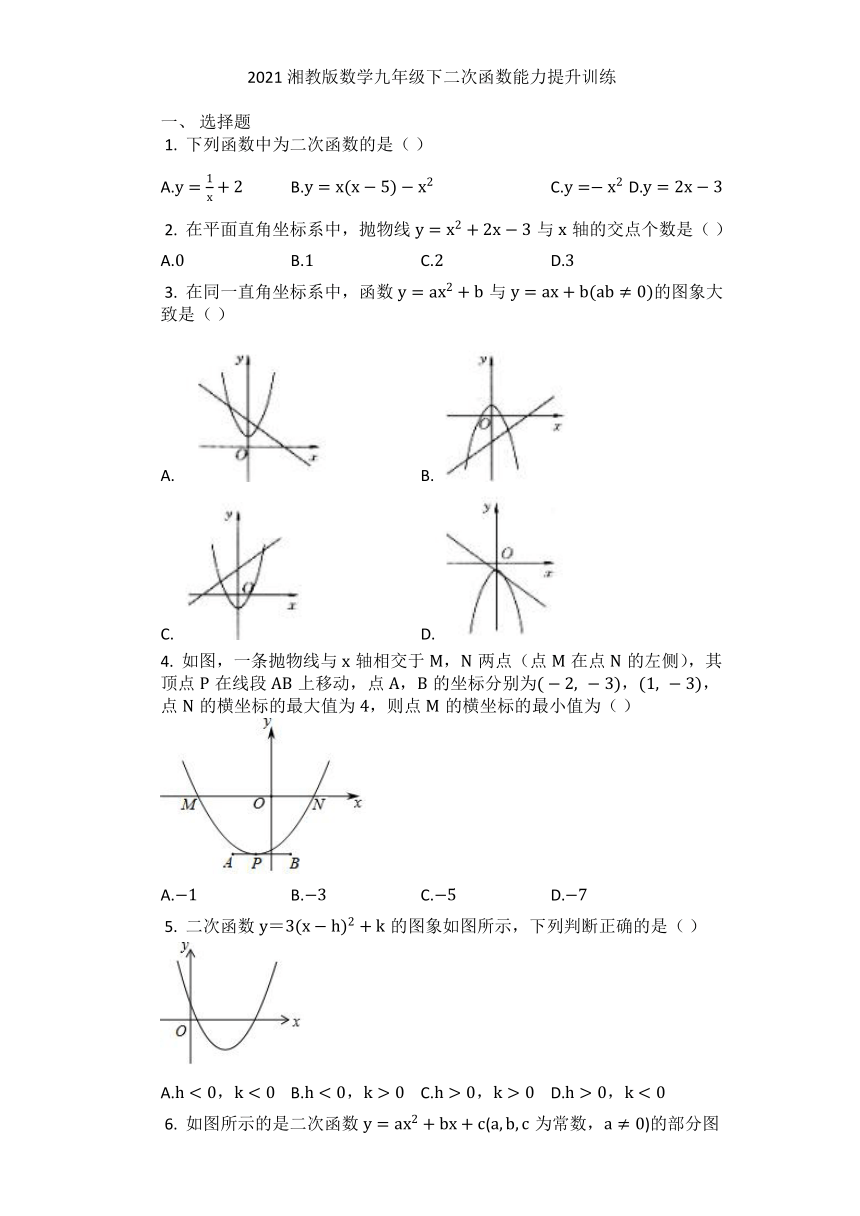 | |
| 格式 | zip | ||
| 文件大小 | 167.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-21 23:24:33 | ||
图片预览




文档简介
2021湘教版数学九年级下二次函数能力提升训练
一、
选择题
?1.
下列函数中为二次函数的是(
)
A.
B.
C.
D.
?2.
在平面直角坐标系中,抛物线与轴的交点个数是(
)
A.
B.
C.
D.
?3.
在同一直角坐标系中,函数与的图象大致是(
)
A.
B.
C.
D.
4.
如图,一条抛物线与轴相交于,两点(点在点的左侧),其顶点在线段上移动,点,的坐标分别为,,点的横坐标的最大值为,则点的横坐标的最小值为(
)
A.
B.
C.
D.
?5.
二次函数=的图象如图所示,下列判断正确的是(
)
A.,
B.,
C.,
D.,
?6.
如图所示的是二次函数(为常数,)的部分图象,由图象可知不等式的解集是(?
?
?
?
)
A.
B.
C.或
D.
?7.
已知抛物线的部分图象如图所示,若,则的取值范围是(
)
A.
B.
C.或
D.或
?8.
如图,一边靠学校院墙,其它三边用米长的篱笆围成一个矩形花圃,设矩形的边米,面积为平方米,则下面关系式正确的是(
)
A.
B.
C.
D.
?9.
已知二次函数的图象上有,,三个点,则,,的大小关系是(?
?
?
?
)
A.
B.
C.
D.
?10.
如图,已知抛物线与轴交于、两点,顶点的纵坐标为,现将抛物线向右平移个单位,得到抛物线,则下列结论:
①;
②;
③阴影部分的面积为;
④若,则.
正确的是(?
?
?
?
)
A.①③
B.②③
C.②④
D.③④
?
11.
在平面直角坐标系中,将抛物线=向右平移个单位长度,平移后的抛物线与轴的交点为,则平移后的抛物线的对称轴为(
)
A.=
B.=
C.=
D.=
?12.
二次函数=,时,当时,随的增大而减小;当时,随的增大而增大,则的值为(
)
A.
B.
C.
D.
?13.
已知函数=,=,当时,,则当时,的最大值是(
)
A.
B.
C.
D.
?14.
二次函数的图象如图所示,直线是该二次函数图象的对称轴,且它的图象开口向下,若点,是它图象上的两点,则与的大小关系是?
?
?
?
?
A.
B.
C.
D.不能确定
?15.
已知抛物线的图像与轴交于、两点(点在点的右侧),与轴交于点给出下列结论:①当的条件下,无论取何值,点是一个定点;②当的条件下,无论取何值,抛物线的对称轴一定位于轴的左侧;③的最小值不大于;④若,则其中正确的结论有(
)个.
A.个
B.个
C.个
D.个
二、
填空题
?
16.
与抛物线关于轴对称的抛物线解析式是________.
17.
二次函数的图像与轴的交点坐标是________.
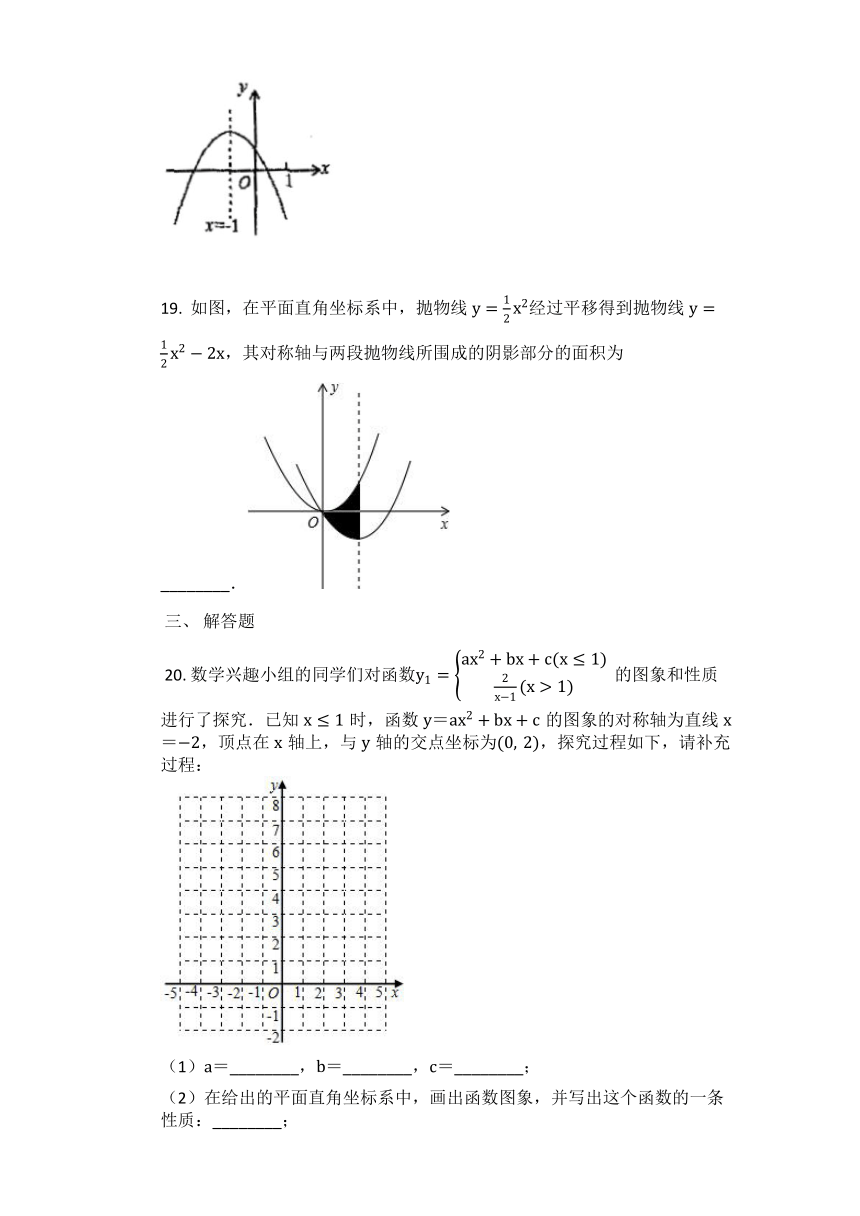
18.
二次函数的图象如图所示,下列结论:①;②;③;④为实数;⑤一元二次方程有两个不等的实数根.上述结论中正确的有________.(填上所有正确结论的序号)
?
19.
如图,在平面直角坐标系中,抛物线经过平移得到抛物线,其对称轴与两段抛物线所围成的阴影部分的面积为________.
三、
解答题
?
?20.
数学兴趣小组的同学们对函数的图象和性质进行了探究.已知时,函数=的图象的对称轴为直线=,顶点在轴上,与轴的交点坐标为,探究过程如下,请补充过程:
(1)=________,=________,=________;
(2)在给出的平面直角坐标系中,画出函数图象,并写出这个函数的一条性质:________;
(3)进一步探究函数图象并解决问题:
①若=有三个实数解,则的取值范围为:________;
②若函数=的图象与该函数有三个交点,则的取值范围为:________.
.
?21.
已知二次函数=的图象经过点
(1)求二次函数的解析式;
(2)当取,时函数值相等,求取时的函数值;
(3)若反比例函数=的图象与中的二次函数的图象在第一象限内的交点为,点的横坐标满足,试求实数的取值范围.
?
22.
已知二次函数.
(1)用配方法将化成的形式;并写出对称轴和顶点坐标.
(2)当时,求的取值范围;
(3)求函数图象与两坐标轴交点所围成的三角形的面积.
?
23阿.
旅游公司在景区内配置了辆观光车供游客租赁使用,假定每辆观光车一天内最多能出租一次,且每辆车的日租金是元,发现每天的营运规律如下:当不超过元时,观光车能全部租出;当超过元时,每辆车的日租金每增加元,租出去的观光车就会减少辆,已知所有观光车每天的管理费是元
若某日的净收入为元,且使游客得到实惠,则当天的观光车的日租金是多少元?(注:净收入租车收入管理费)
设每日净收入为元,请写出与之间的函数关系式;并求出日租金为多少时,每日净收入最大?
参考答案与试题解析
一、
选择题
1.
【答案】
C
【解答】
解:、该函数是由反比例函数平移得到的,不是二次函数,故本选项错误;
、由已知函数解析式得到:,属于正比例函数,故本选项错误;
、该函数符合二次函数的定义,故本选项正确;
、该函数属于一次函数,故本选项错误;
故选:.
2.
【答案】
C
【解答】
解:令得:,
∵
,
∴
抛物线与轴有两个交点.
故选:.
3.
【答案】
D
【解答】
解:、由抛物线可知,,由直线可知,,故本选项错误;
、由抛物线可知,由直线可知,故本选项错误;
、由抛物线可知,,,由直线可知,,,故本选项错误;
、由抛物线可知,,,由直线可知,,,且抛物线顶点在直线上,故本选项正确.
故选.
4.
【答案】
C
【解答】
当图象顶点在点时,点的横坐标的最大值为,
则此时抛物线的表达式为:=,
把点的坐标代入得:=,
解得:,
当顶点在点时,点的横坐标为最小,
此时抛物线的表达式为:,
令=,则=或,
即点的横坐标的最小值为,
5.
【答案】
D
【解答】
观察函数图象可知:顶点在第四象限,
∴
,.
6.
【答案】
C
【解答】
解:由图象得:对称轴是,
与轴的一个交点的坐标为,
∴
图象与轴的另一个交点坐标为.
利用图象可知:
的解集即是的解集,
∴
或.
故选.
7.
【答案】
C
【解答】
解:因为抛物线与轴的交点,对称轴是,
根据抛物线的对称性可得,抛物线与轴的另一个交点;
因为,图象开口向下,
所以,当或时,.
故选.
8.
【答案】
B
【解答】
解:∵
米,
∴
米,
∴
.
故选.
9.
【答案】
A
【解答】
解:由题意知,
二次函数的对称轴为,
在图象上的三点,,三个点,
由于,
故,,的大小关系为.
故选.
10.
【答案】
D
【解答】
解:∵
抛物线开口向上,
∴
,
又∵
对称轴为,
∴
,
∴
结论①不正确;
∵
时,,
∴
,
∴
结论②不正确;
∵
抛物线向右平移了个单位,
∴
平行四边形的底是,
∵
函数的最小值是,
∴
平行四边形的高是,
∴
阴影部分的面积是:,
∴
结论③正确;
∵
,,
∴
,
∴
结论④正确.
综上,结论正确的是:③④.
故选.
11.
【答案】
D
【解答】
∵
抛物线==,
∴
顶点为,
将抛物线=向右平移个单位长度,平移后的顶点为,
∴
平移后的抛物线为=,
∵
移后的抛物线与轴的交点为,
∴
=,
解得=,
∴
=,
∴
平移后的抛物线的对称轴为直线=,
12.
【答案】
B
【解答】
∵
二次函数=,时,当时,随的增大而减小;当时,随的增大而增大,
∴
,
解得,=,
13.
【答案】
D
【解答】
由题意得:当时,函数在对称轴=时取得最小值,即==①,
函数在=时,取得最大值,即==②,
联立①②并解得:,
故==,
当时,在对称轴处取得最大值,
∴
当=时,=,
故最大值是,
14.
【答案】
B
【解答】
解:∵
,,且对称轴,
∴
,两点关于对称,
∴
,两点的纵坐标相等.
∴
.
∴
正确.
故选.
15.
【答案】
C
【解答】
①?.则该抛物线恒过点?.故①符合题意;②.的图象与轴有个交点,
:该抛物线的对称轴为:?,无法判定的正负.
故②不一定符合题意;
③根据抛物线与轴交于可知,的最小值不大于,故③符合题意;
④.?
∴
当时,
解得,故④符合题意.
综上所述,正确的结论有个.
故答案为:.
二、
填空题
16.
【答案】
【解答】
:
∴
顶点()
∴
顶点关于,轴,对称点为且开口向下,
故答案为:
17.
【答案】
【解答】
把弋入?,得
∴
图像与轴的交点坐标是
故答案为:
18.
【答案】
①②⑤
【解答】
解:①因为二次函数图象与轴有两个交点,所以,所以,故①正确;
②由图象可得当时,,故②正确;
③因为二次函数对称轴为,由图可得左交点的横坐标一定小于,所以,即,故③不正确;
④∵
抛物线的对称轴是直线,
∴
的值最大,当时,,故④不正确;
⑤由图可知:二次函数向上平移个单位后与轴同样有个交点,
∴
一元二次方程有两个不等的实数根,故⑤正确.
正确的结论为①②⑤.
故答案为:①②⑤.
19.
【答案】
【解答】
解:如图,∵
,
∴
平移后抛物线的顶点坐标为,对称轴为直线,
当时,,
∴
平移后阴影部分的面积等于如图三角形的面积,
.
故答案为:.
三、
解答题
20.
【答案】
,,
当=时,函数有最小值
,
【解答】
∵
函数=的图象的对称轴为直线=,过,,
则:,
解得:;
由(1)知,,
图象如图所示:
根据图象,可知当=时,函数有最小值;
①由图可知,当时,=有三个实数解,
即若=有三个实数解,则的取值范围为:;
②由图可知,当=与相切时,两个函数图象恰好有两个交点,
把=代入,得=,
∴
=,
∴
==,
解得.
当=过点时,两个函数图象恰好有三个交点,
∴
,解得,
所以满足条件的的取值范围是.
故答案为:,,;当=时,函数有最小值;;.
21.
【答案】
解:将点代入=,解得=
∴
抛物线解析式为
解:由抛物线=可知抛物线与轴的交点为,,
∴
对称轴为直线==,
∵
当取,时函数值相等,
∴
=,
∴
=
∴
==,
取时的函数值为
解:当时,函数=,随着增大而增大,对=,随着的增大而减小.
∵
为二次函数图象与反比例函数图象的交点,
∴
当=时,由反比例函数图象在二次函数上方得,
即,解得
当=时,二次函数数图象在反比例上方得,
即,解得
所以的取值范围为
【解答】
此题暂无解答
22.
【答案】
解:,
∴
抛物线的对称轴为,顶点坐标为
解:当时,有最小值,最小值为,
∵
,
∴
的最大值为.
∴
的取值范围是
解:当时,,
当时,,解得:或,
∴
函数图象与两坐标轴交点所围成的三角形的面积
【解答】
此题暂无解答
23.
【答案】
解:当时,
则有,
解得(舍);
当时,
则,
解得,.
要使游客得到实惠,则当天观光车的日租金是元.
由题意可得
即当时,,
当时,,
则当日租金不超过元时,每日净收入最大为,
当日租金超过元时,每日净收入最大为.
【解答】
解:当时,
则有,
解得(舍);
当时,
则,
解得,.
要使游客得到实惠,则当天观光车的日租金是元.
由题意可得
即当时,,
当时,,
则当日租金不超过元时,每日净收入最大为,
当日租金超过元时,每日净收入最大为.
一、
选择题
?1.
下列函数中为二次函数的是(
)
A.
B.
C.
D.
?2.
在平面直角坐标系中,抛物线与轴的交点个数是(
)
A.
B.
C.
D.
?3.
在同一直角坐标系中,函数与的图象大致是(
)
A.
B.
C.
D.
4.
如图,一条抛物线与轴相交于,两点(点在点的左侧),其顶点在线段上移动,点,的坐标分别为,,点的横坐标的最大值为,则点的横坐标的最小值为(
)
A.
B.
C.
D.
?5.
二次函数=的图象如图所示,下列判断正确的是(
)
A.,
B.,
C.,
D.,
?6.
如图所示的是二次函数(为常数,)的部分图象,由图象可知不等式的解集是(?
?
?
?
)
A.
B.
C.或
D.
?7.
已知抛物线的部分图象如图所示,若,则的取值范围是(
)
A.
B.
C.或
D.或
?8.
如图,一边靠学校院墙,其它三边用米长的篱笆围成一个矩形花圃,设矩形的边米,面积为平方米,则下面关系式正确的是(
)
A.
B.
C.
D.
?9.
已知二次函数的图象上有,,三个点,则,,的大小关系是(?
?
?
?
)
A.
B.
C.
D.
?10.
如图,已知抛物线与轴交于、两点,顶点的纵坐标为,现将抛物线向右平移个单位,得到抛物线,则下列结论:
①;
②;
③阴影部分的面积为;
④若,则.
正确的是(?
?
?
?
)
A.①③
B.②③
C.②④
D.③④
?
11.
在平面直角坐标系中,将抛物线=向右平移个单位长度,平移后的抛物线与轴的交点为,则平移后的抛物线的对称轴为(
)
A.=
B.=
C.=
D.=
?12.
二次函数=,时,当时,随的增大而减小;当时,随的增大而增大,则的值为(
)
A.
B.
C.
D.
?13.
已知函数=,=,当时,,则当时,的最大值是(
)
A.
B.
C.
D.
?14.
二次函数的图象如图所示,直线是该二次函数图象的对称轴,且它的图象开口向下,若点,是它图象上的两点,则与的大小关系是?
?
?
?
?
A.
B.
C.
D.不能确定
?15.
已知抛物线的图像与轴交于、两点(点在点的右侧),与轴交于点给出下列结论:①当的条件下,无论取何值,点是一个定点;②当的条件下,无论取何值,抛物线的对称轴一定位于轴的左侧;③的最小值不大于;④若,则其中正确的结论有(
)个.
A.个
B.个
C.个
D.个
二、
填空题
?
16.
与抛物线关于轴对称的抛物线解析式是________.
17.
二次函数的图像与轴的交点坐标是________.
18.
二次函数的图象如图所示,下列结论:①;②;③;④为实数;⑤一元二次方程有两个不等的实数根.上述结论中正确的有________.(填上所有正确结论的序号)
?
19.
如图,在平面直角坐标系中,抛物线经过平移得到抛物线,其对称轴与两段抛物线所围成的阴影部分的面积为________.
三、
解答题
?
?20.
数学兴趣小组的同学们对函数的图象和性质进行了探究.已知时,函数=的图象的对称轴为直线=,顶点在轴上,与轴的交点坐标为,探究过程如下,请补充过程:
(1)=________,=________,=________;
(2)在给出的平面直角坐标系中,画出函数图象,并写出这个函数的一条性质:________;
(3)进一步探究函数图象并解决问题:
①若=有三个实数解,则的取值范围为:________;
②若函数=的图象与该函数有三个交点,则的取值范围为:________.
.
?21.
已知二次函数=的图象经过点
(1)求二次函数的解析式;
(2)当取,时函数值相等,求取时的函数值;
(3)若反比例函数=的图象与中的二次函数的图象在第一象限内的交点为,点的横坐标满足,试求实数的取值范围.
?
22.
已知二次函数.
(1)用配方法将化成的形式;并写出对称轴和顶点坐标.
(2)当时,求的取值范围;
(3)求函数图象与两坐标轴交点所围成的三角形的面积.
?
23阿.
旅游公司在景区内配置了辆观光车供游客租赁使用,假定每辆观光车一天内最多能出租一次,且每辆车的日租金是元,发现每天的营运规律如下:当不超过元时,观光车能全部租出;当超过元时,每辆车的日租金每增加元,租出去的观光车就会减少辆,已知所有观光车每天的管理费是元
若某日的净收入为元,且使游客得到实惠,则当天的观光车的日租金是多少元?(注:净收入租车收入管理费)
设每日净收入为元,请写出与之间的函数关系式;并求出日租金为多少时,每日净收入最大?
参考答案与试题解析
一、
选择题
1.
【答案】
C
【解答】
解:、该函数是由反比例函数平移得到的,不是二次函数,故本选项错误;
、由已知函数解析式得到:,属于正比例函数,故本选项错误;
、该函数符合二次函数的定义,故本选项正确;
、该函数属于一次函数,故本选项错误;
故选:.
2.
【答案】
C
【解答】
解:令得:,
∵
,
∴
抛物线与轴有两个交点.
故选:.
3.
【答案】
D
【解答】
解:、由抛物线可知,,由直线可知,,故本选项错误;
、由抛物线可知,由直线可知,故本选项错误;
、由抛物线可知,,,由直线可知,,,故本选项错误;
、由抛物线可知,,,由直线可知,,,且抛物线顶点在直线上,故本选项正确.
故选.
4.
【答案】
C
【解答】
当图象顶点在点时,点的横坐标的最大值为,
则此时抛物线的表达式为:=,
把点的坐标代入得:=,
解得:,
当顶点在点时,点的横坐标为最小,
此时抛物线的表达式为:,
令=,则=或,
即点的横坐标的最小值为,
5.
【答案】
D
【解答】
观察函数图象可知:顶点在第四象限,
∴
,.
6.
【答案】
C
【解答】
解:由图象得:对称轴是,
与轴的一个交点的坐标为,
∴
图象与轴的另一个交点坐标为.
利用图象可知:
的解集即是的解集,
∴
或.
故选.
7.
【答案】
C
【解答】
解:因为抛物线与轴的交点,对称轴是,
根据抛物线的对称性可得,抛物线与轴的另一个交点;
因为,图象开口向下,
所以,当或时,.
故选.
8.
【答案】
B
【解答】
解:∵
米,
∴
米,
∴
.
故选.
9.
【答案】
A
【解答】
解:由题意知,
二次函数的对称轴为,
在图象上的三点,,三个点,
由于,
故,,的大小关系为.
故选.
10.
【答案】
D
【解答】
解:∵
抛物线开口向上,
∴
,
又∵
对称轴为,
∴
,
∴
结论①不正确;
∵
时,,
∴
,
∴
结论②不正确;
∵
抛物线向右平移了个单位,
∴
平行四边形的底是,
∵
函数的最小值是,
∴
平行四边形的高是,
∴
阴影部分的面积是:,
∴
结论③正确;
∵
,,
∴
,
∴
结论④正确.
综上,结论正确的是:③④.
故选.
11.
【答案】
D
【解答】
∵
抛物线==,
∴
顶点为,
将抛物线=向右平移个单位长度,平移后的顶点为,
∴
平移后的抛物线为=,
∵
移后的抛物线与轴的交点为,
∴
=,
解得=,
∴
=,
∴
平移后的抛物线的对称轴为直线=,
12.
【答案】
B
【解答】
∵
二次函数=,时,当时,随的增大而减小;当时,随的增大而增大,
∴
,
解得,=,
13.
【答案】
D
【解答】
由题意得:当时,函数在对称轴=时取得最小值,即==①,
函数在=时,取得最大值,即==②,
联立①②并解得:,
故==,
当时,在对称轴处取得最大值,
∴
当=时,=,
故最大值是,
14.
【答案】
B
【解答】
解:∵
,,且对称轴,
∴
,两点关于对称,
∴
,两点的纵坐标相等.
∴
.
∴
正确.
故选.
15.
【答案】
C
【解答】
①?.则该抛物线恒过点?.故①符合题意;②.的图象与轴有个交点,
:该抛物线的对称轴为:?,无法判定的正负.
故②不一定符合题意;
③根据抛物线与轴交于可知,的最小值不大于,故③符合题意;
④.?
∴
当时,
解得,故④符合题意.
综上所述,正确的结论有个.
故答案为:.
二、
填空题
16.
【答案】
【解答】
:
∴
顶点()
∴
顶点关于,轴,对称点为且开口向下,
故答案为:
17.
【答案】
【解答】
把弋入?,得
∴
图像与轴的交点坐标是
故答案为:
18.
【答案】
①②⑤
【解答】
解:①因为二次函数图象与轴有两个交点,所以,所以,故①正确;
②由图象可得当时,,故②正确;
③因为二次函数对称轴为,由图可得左交点的横坐标一定小于,所以,即,故③不正确;
④∵
抛物线的对称轴是直线,
∴
的值最大,当时,,故④不正确;
⑤由图可知:二次函数向上平移个单位后与轴同样有个交点,
∴
一元二次方程有两个不等的实数根,故⑤正确.
正确的结论为①②⑤.
故答案为:①②⑤.
19.
【答案】
【解答】
解:如图,∵
,
∴
平移后抛物线的顶点坐标为,对称轴为直线,
当时,,
∴
平移后阴影部分的面积等于如图三角形的面积,
.
故答案为:.
三、
解答题
20.
【答案】
,,
当=时,函数有最小值
,
【解答】
∵
函数=的图象的对称轴为直线=,过,,
则:,
解得:;
由(1)知,,
图象如图所示:
根据图象,可知当=时,函数有最小值;
①由图可知,当时,=有三个实数解,
即若=有三个实数解,则的取值范围为:;
②由图可知,当=与相切时,两个函数图象恰好有两个交点,
把=代入,得=,
∴
=,
∴
==,
解得.
当=过点时,两个函数图象恰好有三个交点,
∴
,解得,
所以满足条件的的取值范围是.
故答案为:,,;当=时,函数有最小值;;.
21.
【答案】
解:将点代入=,解得=
∴
抛物线解析式为
解:由抛物线=可知抛物线与轴的交点为,,
∴
对称轴为直线==,
∵
当取,时函数值相等,
∴
=,
∴
=
∴
==,
取时的函数值为
解:当时,函数=,随着增大而增大,对=,随着的增大而减小.
∵
为二次函数图象与反比例函数图象的交点,
∴
当=时,由反比例函数图象在二次函数上方得,
即,解得
当=时,二次函数数图象在反比例上方得,
即,解得
所以的取值范围为
【解答】
此题暂无解答
22.
【答案】
解:,
∴
抛物线的对称轴为,顶点坐标为
解:当时,有最小值,最小值为,
∵
,
∴
的最大值为.
∴
的取值范围是
解:当时,,
当时,,解得:或,
∴
函数图象与两坐标轴交点所围成的三角形的面积
【解答】
此题暂无解答
23.
【答案】
解:当时,
则有,
解得(舍);
当时,
则,
解得,.
要使游客得到实惠,则当天观光车的日租金是元.
由题意可得
即当时,,
当时,,
则当日租金不超过元时,每日净收入最大为,
当日租金超过元时,每日净收入最大为.
【解答】
解:当时,
则有,
解得(舍);
当时,
则,
解得,.
要使游客得到实惠,则当天观光车的日租金是元.
由题意可得
即当时,,
当时,,
则当日租金不超过元时,每日净收入最大为,
当日租金超过元时,每日净收入最大为.
