山东省新泰市2020-2021学年六年级下学期期末数学模拟试题(word版 含答案)
文档属性
| 名称 | 山东省新泰市2020-2021学年六年级下学期期末数学模拟试题(word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 534.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-22 05:41:34 | ||
图片预览


文档简介
2020--2021第二学期期末六年级数学模拟试题
一、选择题(每题4分,共48分)
1.年月日,北斗三号最后一颗全球组网卫星在西昌卫星发射中心点火升空.北斗卫星导航系统可提供高精度的授时服务,授时精度可达纳秒(秒=纳秒)用科学记数法表示纳秒为( )
A.秒 B.秒 C.秒 D.秒
2.下列运算正确的是( )
A.(﹣2a3)2=4a6 B.a2?a3=a6 C.3a+a2=3a3 D.(a﹣b)2=a2﹣b2
3.在下列多项式的乘法中,可以用平方差公式计算的是( )
A. B. C. D.
4.以下调查中,最适合采用全面调查的是( )
A.检测长征运载火箭的零部件质量情况 B.了解全国中小学生课外阅读情况
C.调查某批次汽车的抗撞击能力 D.检测某城市的空气质量
5.如图所示,下列说法正确的是( )
A.与是内错角 B.与是同位角
C.与∠B是同旁内角 D.与是内错角
第5题图 第7题图 第8题图
6.如图所示,下列条件能判断a∥b的有( )
A.∠1+∠2=180° B.∠2=∠4 C.∠2+∠3=180° D.∠1=∠3
7.点C是线段AB中点,点D是线段AC三等分点.若线段,则线段BD的长为( )
A.10cm B.8cm C.8cm或10cm D.2cm或4cm
8.如图,若点A、O、B在一条直线上,平分,,当时,则( )
A. B. C. D.
9.若计算所得的结果中不含的一次项,则常数的值为( )
A. B. C.0 D.2
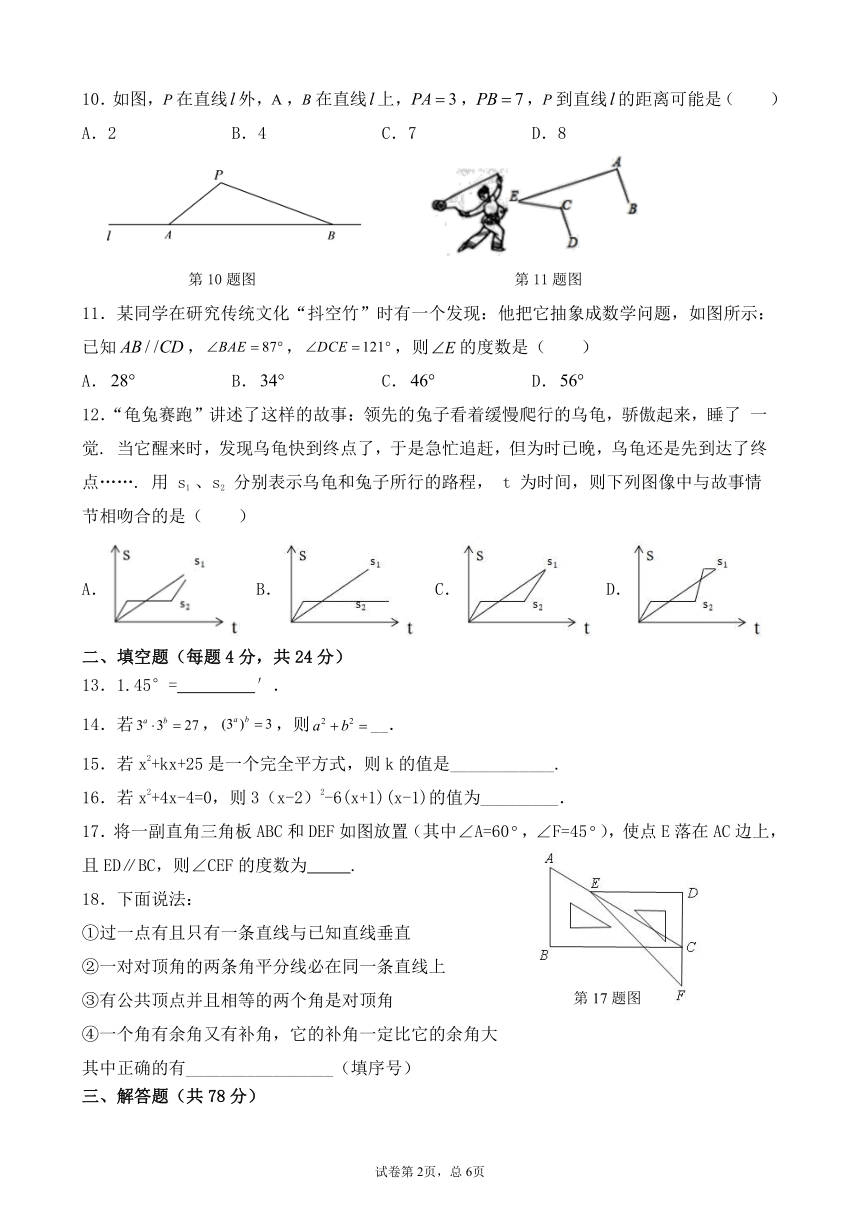
10.如图,在直线外,,在直线上,,,到直线的距离可能是( )
A.2 B.4 C.7 D.8
第10题图 第11题图
11.某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示:已知,,,则的度数是( )
A. B. C. D.
12.“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了 一觉. 当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终 点……. 用 s1 、s2 分别表示乌龟和兔子所行的路程, t 为时间,则下列图像中与故事情节相吻合的是( )
A. B. C. D.
二、填空题(每题4分,共24分)
13.1.45°= ′.
14.若,,则__.
15.若x2+kx+25是一个完全平方式,则k的值是____________.
16.若x2+4x-4=0,则3(x-2)2-6(x+1)(x-1)的值为_________.
17.将一副直角三角板ABC和DEF如图放置(其中∠A=60,∠F=45),使点E落在AC边上,且ED∥BC,则∠CEF的度数为 .
18.下面说法:
①过一点有且只有一条直线与已知直线垂直
②一对对顶角的两条角平分线必在同一条直线上
③有公共顶点并且相等的两个角是对顶角
④一个角有余角又有补角,它的补角一定比它的余角大
其中正确的有_________________(填序号)
三、解答题(共78分)
19.(每题4分,共16分)计算:
(1)﹣14+(﹣2)3+(π﹣3.14)0+(﹣)﹣2; (2)(﹣a)3?a5+(﹣4a4)2;
(3)(3ab3﹣a2b+ab)÷(﹣ab); (4)简便运算:2021×2019-20202
20.(每题8分,共16分)先化简,再求值:
(1)(2a﹣b)2+(a+1﹣b)(a+1+b)﹣(a+1)2,其中a=,b=﹣2.
(2)2b2+(a+b)(a-b)-(a-b)2,其中a=-3,b=.
21.(8分)如图,直线分别与直线,交于点,.平分,平分,且∥.求证:∥.
22.(8分)如图所示,点P,Q在线段AB上中点C的同一侧,点P分AB为2:3,点Q分AB为3:4,若PQ=2 cm,则AB的长为多少?
23.(9分)小南一家到某度假村度假.小南和妈妈坐公交车先出发,爸爸自驾车沿着相同的道路后出发.爸爸到达度假村后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往度假村(取东西的时间忽略不计).如下图是他们离家的距离s(km)与小南离家的时间t(h)的关系图.请根据图回答下列问题:
(1)图中的自变量是_________,因变量是_________,小南家到该度假村的距离是_____km.
(2)小南出发___________小时后爸爸驾车出发,爸爸驾车的平均速度为___________km/h,图中点A表示 .
(3)小南从家到度假村的路途中,当他与爸爸相遇时,离家的距离约是___________km.
24.(10分)如图,某市有一块长为米,宽为米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,左右两边修两条宽为a米的道路.().
(1)试用含a,b的代数式表示绿化的面积是多少平方米?
(2)若,请求出绿化面积.
25.(11分)由于疫情的影响,学生不能返校上课,某校在直播授课的同时还为学生提供了四种辅助学习方式:A网上自测,B网上阅读,C网上答疑,D网上讨论.为了解学生对四种学习方式的喜欢情况,该校随机抽取部分学生进行问卷调查,规定被调查学生从四种方式中选择自己最喜欢的一种,根据调查结果绘制成如下两幅不完整的统计图:
根据统计图提供的信息,解答下列问题:
(1)本次共调查了____________名学生;
(2)在扇形统计图中,m的值是___________,D对应的扇形圆心角的度数是________________;
(3)请补全条形统计图;
(4)若该校共有2000名学生,根据抽样调查的结果,请你估计该校最喜欢方式D的学生人数.
数学试题答案
一、选择题
AACAC BCCDA BA
填空题
13.87′. 14.7 15.±10. 16.6 17.15 18.②④
三、解答题
19.(1)1;(2)15a8;(3)-6 b2+2a-1;(4)-1
20.(1)4a2﹣4ab ,5 (2),-3
21.证明:平分,平分
……………………2分
………………………………………………4分
,即…………………6分
.……………………………………………………8分
解:∵点P分AB为2:3,点Q分AB为3:4,
∴AP=AB,AQ=AB,…………………………………………2分
∵PQ=2cm,
∴PQ=AQ-AP=AB-AB=AB=2,…………………………6分
解得AB=70;…………………………………………………………8分
(也可用方程)
(每小题3分,共9分)
(1)时间或t,距离或s,60;
(2)1,60,小亮出发2.5小时后,离度假村的距离为10km(描述有2.5和10,合理即可);
(3)30或45.
24.解:(1)由题意可得:
(3a+b)(2a+b)-(a+b)2-a(3a+b-a-b)
=6a2+5ab+b2-a2-2ab-b2-2a2
=(3a2+3ab)平方米;
答:绿化的面积是(3a2+3ab)平方米;……………………………………6分
(2)当a=30,b=20,
绿化面积是3a2+3ab=3×900+3×30×20=4500平方米.
答:绿化面积是4500平方米。…………………………………………10分
25.(1)50;……………………………………………………2分
(2)30,;………………………………………………6分
(3)
………………………………8分
(4)(人).
答:该校最喜欢方式D的学生约有400人.…………………………………11分
试卷第1 11页,总3 33页
试卷第1 11页,总3 33页
一、选择题(每题4分,共48分)
1.年月日,北斗三号最后一颗全球组网卫星在西昌卫星发射中心点火升空.北斗卫星导航系统可提供高精度的授时服务,授时精度可达纳秒(秒=纳秒)用科学记数法表示纳秒为( )
A.秒 B.秒 C.秒 D.秒
2.下列运算正确的是( )
A.(﹣2a3)2=4a6 B.a2?a3=a6 C.3a+a2=3a3 D.(a﹣b)2=a2﹣b2
3.在下列多项式的乘法中,可以用平方差公式计算的是( )
A. B. C. D.
4.以下调查中,最适合采用全面调查的是( )
A.检测长征运载火箭的零部件质量情况 B.了解全国中小学生课外阅读情况
C.调查某批次汽车的抗撞击能力 D.检测某城市的空气质量
5.如图所示,下列说法正确的是( )
A.与是内错角 B.与是同位角
C.与∠B是同旁内角 D.与是内错角
第5题图 第7题图 第8题图
6.如图所示,下列条件能判断a∥b的有( )
A.∠1+∠2=180° B.∠2=∠4 C.∠2+∠3=180° D.∠1=∠3
7.点C是线段AB中点,点D是线段AC三等分点.若线段,则线段BD的长为( )
A.10cm B.8cm C.8cm或10cm D.2cm或4cm
8.如图,若点A、O、B在一条直线上,平分,,当时,则( )
A. B. C. D.
9.若计算所得的结果中不含的一次项,则常数的值为( )
A. B. C.0 D.2
10.如图,在直线外,,在直线上,,,到直线的距离可能是( )
A.2 B.4 C.7 D.8
第10题图 第11题图
11.某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示:已知,,,则的度数是( )
A. B. C. D.
12.“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了 一觉. 当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终 点……. 用 s1 、s2 分别表示乌龟和兔子所行的路程, t 为时间,则下列图像中与故事情节相吻合的是( )
A. B. C. D.
二、填空题(每题4分,共24分)
13.1.45°= ′.
14.若,,则__.
15.若x2+kx+25是一个完全平方式,则k的值是____________.
16.若x2+4x-4=0,则3(x-2)2-6(x+1)(x-1)的值为_________.
17.将一副直角三角板ABC和DEF如图放置(其中∠A=60,∠F=45),使点E落在AC边上,且ED∥BC,则∠CEF的度数为 .
18.下面说法:
①过一点有且只有一条直线与已知直线垂直
②一对对顶角的两条角平分线必在同一条直线上
③有公共顶点并且相等的两个角是对顶角
④一个角有余角又有补角,它的补角一定比它的余角大
其中正确的有_________________(填序号)
三、解答题(共78分)
19.(每题4分,共16分)计算:
(1)﹣14+(﹣2)3+(π﹣3.14)0+(﹣)﹣2; (2)(﹣a)3?a5+(﹣4a4)2;
(3)(3ab3﹣a2b+ab)÷(﹣ab); (4)简便运算:2021×2019-20202
20.(每题8分,共16分)先化简,再求值:
(1)(2a﹣b)2+(a+1﹣b)(a+1+b)﹣(a+1)2,其中a=,b=﹣2.
(2)2b2+(a+b)(a-b)-(a-b)2,其中a=-3,b=.
21.(8分)如图,直线分别与直线,交于点,.平分,平分,且∥.求证:∥.
22.(8分)如图所示,点P,Q在线段AB上中点C的同一侧,点P分AB为2:3,点Q分AB为3:4,若PQ=2 cm,则AB的长为多少?
23.(9分)小南一家到某度假村度假.小南和妈妈坐公交车先出发,爸爸自驾车沿着相同的道路后出发.爸爸到达度假村后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往度假村(取东西的时间忽略不计).如下图是他们离家的距离s(km)与小南离家的时间t(h)的关系图.请根据图回答下列问题:
(1)图中的自变量是_________,因变量是_________,小南家到该度假村的距离是_____km.
(2)小南出发___________小时后爸爸驾车出发,爸爸驾车的平均速度为___________km/h,图中点A表示 .
(3)小南从家到度假村的路途中,当他与爸爸相遇时,离家的距离约是___________km.
24.(10分)如图,某市有一块长为米,宽为米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,左右两边修两条宽为a米的道路.().
(1)试用含a,b的代数式表示绿化的面积是多少平方米?
(2)若,请求出绿化面积.
25.(11分)由于疫情的影响,学生不能返校上课,某校在直播授课的同时还为学生提供了四种辅助学习方式:A网上自测,B网上阅读,C网上答疑,D网上讨论.为了解学生对四种学习方式的喜欢情况,该校随机抽取部分学生进行问卷调查,规定被调查学生从四种方式中选择自己最喜欢的一种,根据调查结果绘制成如下两幅不完整的统计图:
根据统计图提供的信息,解答下列问题:
(1)本次共调查了____________名学生;
(2)在扇形统计图中,m的值是___________,D对应的扇形圆心角的度数是________________;
(3)请补全条形统计图;
(4)若该校共有2000名学生,根据抽样调查的结果,请你估计该校最喜欢方式D的学生人数.
数学试题答案
一、选择题
AACAC BCCDA BA
填空题
13.87′. 14.7 15.±10. 16.6 17.15 18.②④
三、解答题
19.(1)1;(2)15a8;(3)-6 b2+2a-1;(4)-1
20.(1)4a2﹣4ab ,5 (2),-3
21.证明:平分,平分
……………………2分
………………………………………………4分
,即…………………6分
.……………………………………………………8分
解:∵点P分AB为2:3,点Q分AB为3:4,
∴AP=AB,AQ=AB,…………………………………………2分
∵PQ=2cm,
∴PQ=AQ-AP=AB-AB=AB=2,…………………………6分
解得AB=70;…………………………………………………………8分
(也可用方程)
(每小题3分,共9分)
(1)时间或t,距离或s,60;
(2)1,60,小亮出发2.5小时后,离度假村的距离为10km(描述有2.5和10,合理即可);
(3)30或45.
24.解:(1)由题意可得:
(3a+b)(2a+b)-(a+b)2-a(3a+b-a-b)
=6a2+5ab+b2-a2-2ab-b2-2a2
=(3a2+3ab)平方米;
答:绿化的面积是(3a2+3ab)平方米;……………………………………6分
(2)当a=30,b=20,
绿化面积是3a2+3ab=3×900+3×30×20=4500平方米.
答:绿化面积是4500平方米。…………………………………………10分
25.(1)50;……………………………………………………2分
(2)30,;………………………………………………6分
(3)
………………………………8分
(4)(人).
答:该校最喜欢方式D的学生约有400人.…………………………………11分
试卷第1 11页,总3 33页
试卷第1 11页,总3 33页
同课章节目录
