《第9章变量之间的关系》期末复习培优提升训练 2020-2021学年鲁教版数学六年级下册(Word版 附答案)
文档属性
| 名称 | 《第9章变量之间的关系》期末复习培优提升训练 2020-2021学年鲁教版数学六年级下册(Word版 附答案) |  | |
| 格式 | doc | ||
| 文件大小 | 190.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-22 11:00:37 | ||
图片预览



文档简介
2021年鲁教版六年级数学下册《第9章变量之间的关系》期末复习培优提升训练(附答案)
1.已知食用油的沸点一般都在200℃以上,下表所示的是小林加热食用油的过程中,几次测量食用油温度的情况:
时间t/s 0 10 20 30 40
油温y/℃ 10 30 50 70 90
则下列说法不正确的是( )
A.没有加热时,油的温度是10℃
B.继续加热到50s,预计油的温度是110℃
C.每加热10s,油的温度升高30℃
D.在这个问题中,自变量为时间t
2.以下四种情境分别描述了两个变量之间的关系:甲:小明投篮时,投出去的篮球的高度与时间的关系;乙:小明去水果店购买同单价的水果,支付费用与水果重量的关系;丙:小明使用的是一种有月租且只包含流量的套餐,则他每月所付话费与通话时间的关系;丁:小明去外婆家吃饭,饭后,按原速度原路返回,小明离家的距离与时间的关系,如图,用图象法刻画上述情境,排序正确的图象顺序是( )
A.①②③④ B.①③④② C.①③②④ D.①④②③
3.如图,反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,热后回家,其中x表示时间,y表示小明离家的距离,小明家、食堂,图书馆在同一直线上,根据图中提供的信息,有下列说法,其中不正确的是( )
A.食堂离小明家0.4km B.小明从食堂到图书馆用了3min
C.图书馆在小明家和食堂之间 D.小明从图书馆回家的平均速度是0.04km/min
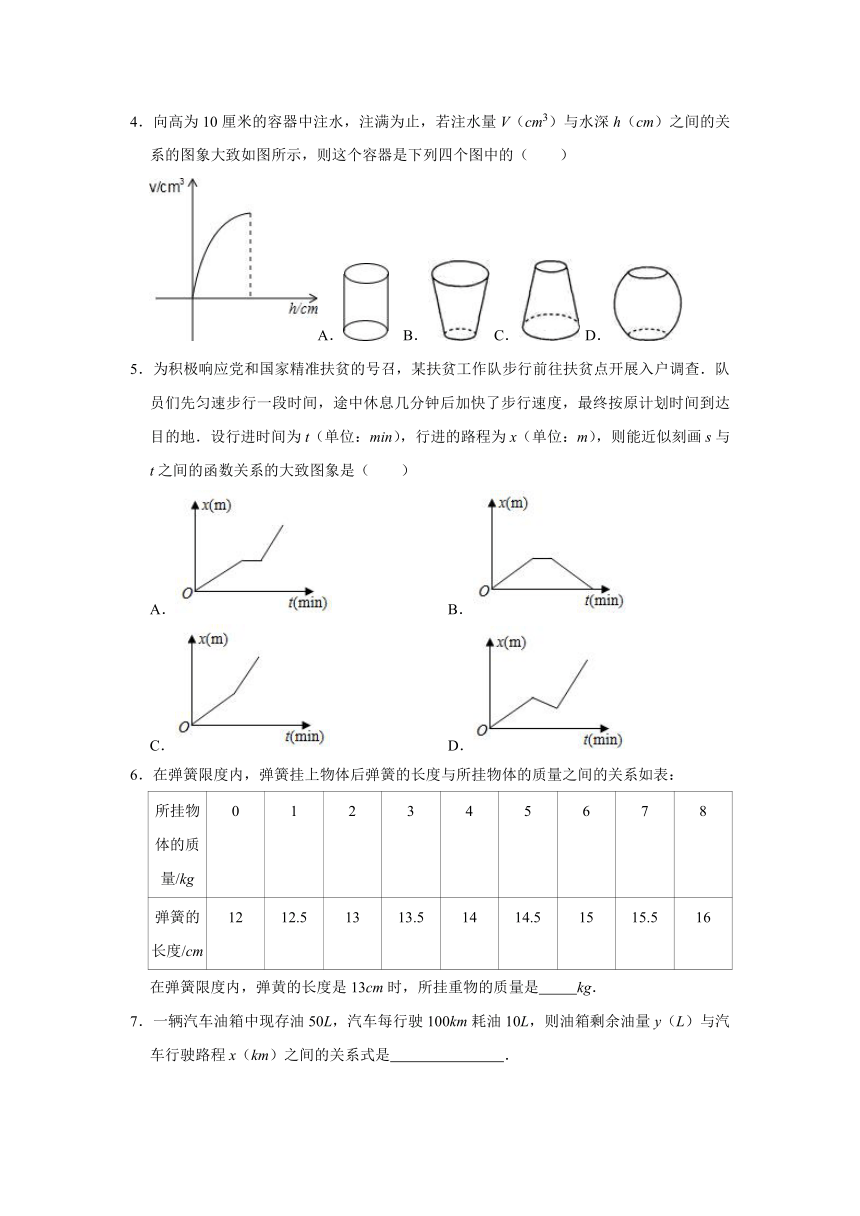
4.向高为10厘米的容器中注水,注满为止,若注水量V(cm3)与水深h(cm)之间的关系的图象大致如图所示,则这个容器是下列四个图中的( )
A. B. C. D.
5.为积极响应党和国家精准扶贫的号召,某扶贫工作队步行前往扶贫点开展入户调查.队员们先匀速步行一段时间,途中休息几分钟后加快了步行速度,最终按原计划时间到达目的地.设行进时间为t(单位:min),行进的路程为x(单位:m),则能近似刻画s与t之间的函数关系的大致图象是( )
A. B.
C. D.
6.在弹簧限度内,弹簧挂上物体后弹簧的长度与所挂物体的质量之间的关系如表:
所挂物体的质量/kg 0 1 2 3 4 5 6 7 8
弹簧的长度/cm 12 12.5 13 13.5 14 14.5 15 15.5 16
在弹簧限度内,弹黄的长度是13cm时,所挂重物的质量是 kg.
7.一辆汽车油箱中现存油50L,汽车每行驶100km耗油10L,则油箱剩余油量y(L)与汽车行驶路程x(km)之间的关系式是 .
8.如图所示的折线ABC为某地向香港地区打电话需付的通话费y(元)与通话时间t(min)之间的函数关系,则通话8min应付通话费 元.
9.为鼓励节约用水,某市规定:每月每户用水不超过10m3,按每立方米1.5元收取水费;若每月每户用水超过10m3,则超过部分每立方米另加收0.5元.设每月每户的用水量为x(m3),应交水费为y(元),试写出当用水量超过10m3时,水费y(元)与用水量x(m3)之间的函数表达式: .若某户某月交水费25元,则该用户当月用水 m3.
10.为了解某品牌轿车的耗油情况,将油箱加满后进行了耗油试验,得到如表数据:
轿车行驶的路程s(km) 0 10 20 30 40 …
油箱剩余油量w(L) 50 49.2 48.4 47.6 46.8 …
(1)在这个变化过程中,自变量是 ,因变量是 ;
(2)该轿车油箱的容量为 L,行驶50km时,油箱剩余油量为 L.
(3)根据如表的数据,写出油箱剩余油量w(L)与轿车行驶的路程s(km)之间的表达式 .
11.如图表示的是汽车在行驶的过程中,速度随时间变化而变化的情况.
(1)汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?
(2)汽车在哪些时间段保持匀速行驶?时速分别是多少?
(3)出发后8分到10分之间可能发生了什么情况?
(4)求汽车从出发后第18分钟到第22分钟行驶的路程.
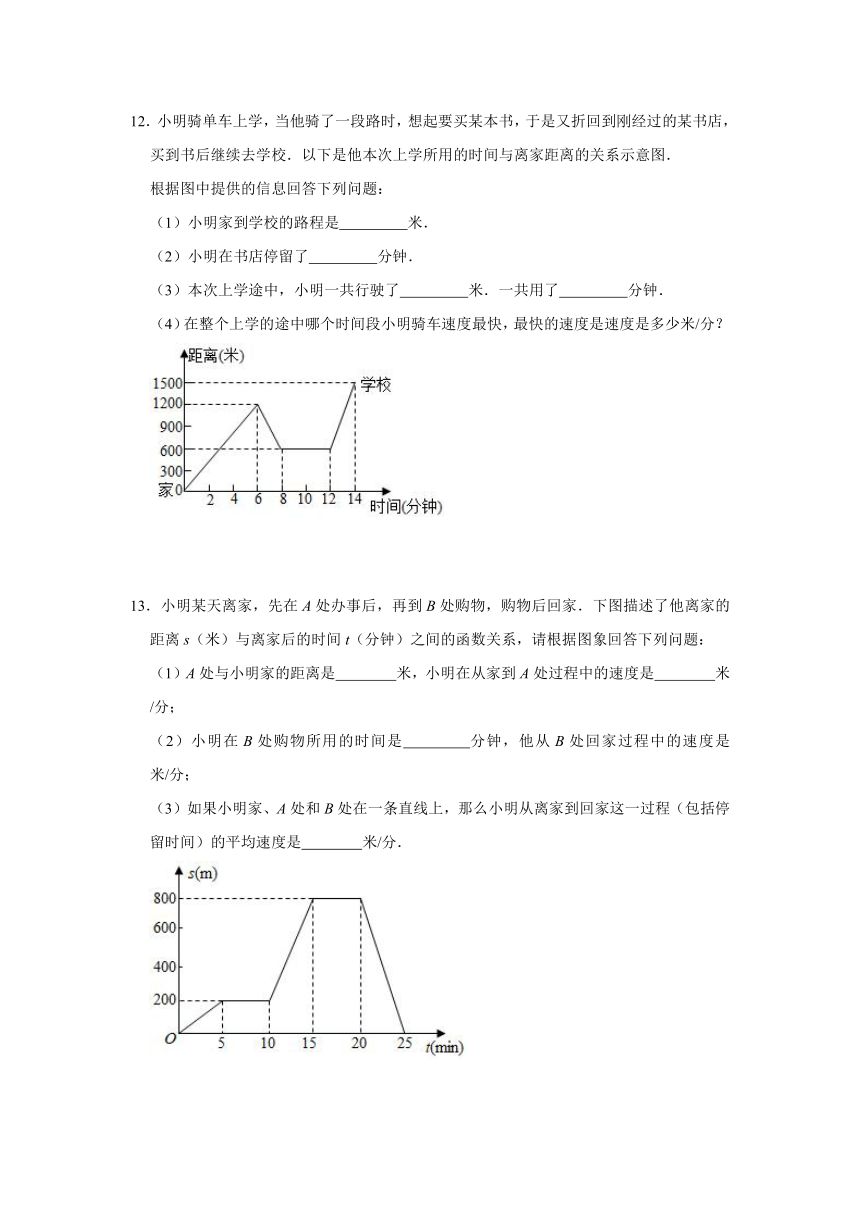
12.小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与离家距离的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是 米.
(2)小明在书店停留了 分钟.
(3)本次上学途中,小明一共行驶了 米.一共用了 分钟.
(4)在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是速度是多少米/分?
13.小明某天离家,先在A处办事后,再到B处购物,购物后回家.下图描述了他离家的距离s(米)与离家后的时间t(分钟)之间的函数关系,请根据图象回答下列问题:
(1)A处与小明家的距离是 米,小明在从家到A处过程中的速度是 米/分;
(2)小明在B处购物所用的时间是 分钟,他从B处回家过程中的速度是 米/分;
(3)如果小明家、A处和B处在一条直线上,那么小明从离家到回家这一过程(包括停留时间)的平均速度是 米/分.
14.小明家所在地的供电公司实行“峰谷电价”,峰时(8:00~21:00)电价为0.5元/度,谷时(21:00~8:00)电价为0.3元/度.为了解空调制暖的耗能情况,小明记录了家里某天0时~24时内空调制暖的用电量,其用电量y(度)与时间x(h)的函数关系如图所示.
(1)小明家白天不开空调的时间共 h;
(2)求小明家该天空调制暖所用的电费;
(3)设空调制暖所用电费为w元,请画出该天0时~24时内w与x的函数图象.(标注必要数据)
15.父亲告诉小明:“距离地面越高,温度越低”,并给小明出示了下面的表格:
距离地面高度(千米)h 0 1 2 3 4 5
温度(℃)t 20 14 8 2 ﹣4 ﹣10
根据表中,父亲还给小明出了下面几个问题,你和小明一起回答.
(1)表中自变量是 ;因变量是 ;当地面上(即h=0时)时,温度是 ℃.
(2)如果用h表示距离地面的高度,用t表示温度,请写出满足h与t关系的式子.
(3)计算出距离地面6千米的高空温度是多少?
16.在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下表是测得的弹簧的长度y与所挂物体的质量x的几组对应值.
所挂物体质量x/kg 0 1 2 3 4 5
弹簧长度y/cm 18 20 22 24 26 28
(1)上述表格反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)写出弹簧长度y(cm)与所挂物体质量x(kg)的关系式.
(3)当所挂重物为3kg时,弹簧有多长?不挂重物呢?
(4)若弹簧的长度为30cm时,此时所挂重物的质量是多少?(在弹簧的允许范围内).
17.某城市为了加强公民的节气和用气意识,按以下规定收取每月煤气费:所用煤气如果不超过50立方米,按每立方米0.8元收费;如果超过50立方米,超过部分按每立方米1.2元收费.设小丽家每月用气量为x立方米,应交煤气费为y元.
(1)若小丽家某月用煤气量为80立方米,则小丽家该月应交煤气费多少元?
(2)试写出y与x之间的表达式;
(3)若小丽家4月份的煤气费为88元,那么她家4月份所用煤气为多少立方米?
(4)已知小丽家6月份的煤气费平均每立方米0.95元,那么6月份小丽家用了多少立方米的煤气?
18.小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米/分?
(3)小明在书店停留了多少分钟?
(4)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
19.一列快车、一列慢车同时从相距300km的两地出发,相向而行.如图,l1和l2分别表示两车到甲地的距离s(km)与行驶时间t(h)的关系.
(1)快车的速度为 km/h,慢车的速度为 km/h;
(2)经过多久两车第一次相遇?
(3)当快车到达目的地时,慢车距离目的地多远?
20.“十一”期间,小明和父母一起开车到距家200km的景点旅游,出发前,汽车油箱内储油45L,当行驶150km时,发现油箱余油量为30L.(假设行驶过程中汽车的耗油量是均匀的)
(1)求该车平均每千米的耗油量,并写出行驶路程x(km)与剩余油量Q(L)的关系式;
(2)当x=280时,求剩余油量Q.
参考答案
1.解:从表格可知:t=0时,y=10,即没有加热时,油的温度为10℃;
每增加10秒,温度上升20℃,则50秒时,油温度110℃;
110秒时,温度230℃;
在这个问题中,自变量为时间t.
故选:C.
2.解:①篮球运动员投篮时,抛出去的篮的高度变大后逐渐变小至0;
②小明去水果店购买同单价的水果,所付费用与水果重量成正比例关系;
③小明使用的是一种有月租且只包含流量的套餐,他每月所付话费与通话时间的关系是一次函数关系;
④小明去外婆家吃饭,小亮离家的距离从0开始变大,到达外婆家吃饭的时候与家的距离不变,返回时与家的距离变小直至为0.
故顺序为①④②③.
故选:D.
3.解:由纵坐标看出:家到食堂的距离是0.6km,故A不正确,符合题意;
由横坐标看出:小明从食堂到图书馆用了28﹣25=3(min),故B正确,不符合题意;
∵家到食堂的距离是0.6km,家到图书馆的距离是0.4km,0.6cm>0.4cm,
∴图书馆在小明家和食堂之间,
故C正确,不符合题意;
小明从图书馆回家所用的时间为:68﹣58=10(min),
∴小明从图书馆回家的平均速度是:0.4÷10=0.04(km/min),
故D正确,不符合题意;
故选:A.
4.解:根据函数图象可知,注水量V(cm3)与水深h(cm)之间的关系是注水量V(cm3)随着h的增大而增加的速度逐渐减慢,可以得出开始容器由大逐渐变小,即开口越来越小,从图形容器可以看出C符合,
故选:C.
5.解:根据题意得:扶贫工作队行刚开始步行的过程,路程缓慢增加;
途中休息几分钟的过程,路程不变;
加快了步行速度的过程,路程快速增加;
综上可得A选项的函数图象符合.
故选:A.
二.填空题(共4小题)
6.解:从表格中找到当弹簧的长度是13cm时,所挂物体的质量为2kg.
故答案为:2.
7.解:∵汽车每行驶100km耗油10L,
∴汽车行驶路程xkm耗油0.1xL,
∵汽车油箱中现存油50L,
∴油箱剩余油量y(L)与汽车行驶路程x(km)之间的关系式是y=﹣0.1x+50.
故答案是:y=﹣0.1x+50.
8.解:由图象可得,点B(3,2.4),C(5,4.4),
设射线BC的解析式为y=kt+b(t≥3),
则,
解得:,
所以,射线BC的解析式为y=t﹣0.6(t≥3),
当t=8时,y=8﹣0.6=7.4(元),
故答案为:7.4.
9.解:y=1.5×10+(1.5+0.5)(x﹣10)
=2x﹣5,
∵25>1.5×10,
∴用水量超过10m3,
当y=25时,即25=2x﹣5,
解得x=15,
故答案为:y=2x﹣5,15.
三.解答题(共5小题)
10.解;(1)由题意可得,自变量为s,因变量为w;
故答案为:s,w;
(2)根据题意,∵当s=0时,邮箱剩余油量为50L,
∴该轿车邮箱的容量为50L,
∵10公里耗油为0.8L,
∴50公里耗油为4L,
∴行驶50km时,油箱剩余油量为46L;
故答案为:50,46;
(3)设油箱剩余油量w(L)与轿车行驶的路程s(km)之间的表达式为w=ks+b,
把把(0,50)和(10,49.2)代入上式,
得,
解得,
∴油箱剩余油量w(L)与轿车行驶的路程s(km)之间的表达式为w=﹣.
故答案为:w=﹣.
11.解:(1)汽车从出发到最后停止共经过了24min,它的最高时速是75km/h;
(2)汽车在2min到6min,18min到22min保持匀速行驶,时速分别是25km/h和75km/h;
(3)汽车出发8min到10min之间处于静止状态,可能是遇到红灯等情况;
(4)汽车从出发后第18分钟到第22分钟行驶的路程=75×=5(km).
12.解:根据小明本次上学所用的时间与离家距离的关系示意图可知:
(1)小明家到学校的路程是1500米;
故答案为:1500.
(2)小明在书店停留了12﹣8=4(分钟);
故答案为:4.
(3)本次上学途中,小明一共行驶了1200+600+(1500﹣600)=2700(米),一共用了14分钟;
故答案为:2700;14.
(4)在整个上学的途中12分钟至14分钟小明骑车速度最快,最快的速度为:(米/分);
∴在整个上学的途中12分钟至14分钟小明骑车速度最快,最快的速度为:450米/分.
13.解:(1)由图可知,x=5时小明到达A处,A处离家距离为200米;
200÷5=40(米/分).
(2)10﹣5=5(分);
800÷(25﹣20)=160(米/分).
(3)小明往返所走路程为800×2=1600(米),往返所用时间为25分.
∴1600÷25=64(米/分).
故答案为:(1)200,40;
(2)5,160;
(3)64.
14.解:(1)小明家白天不开空调的时间为:18﹣8=10(h),
故答案为:10;
(2)峰时所用电费为:3×3×0.5=4.5(元),
谷时所用电费为:11×3×0.3=9.9(元),
所以小明家该天空调制暖所用的电费为:4.5+9.9=14.4(元);
(3)根据题意,可得该天0时~24时内w与x的函数图象如下:
15.解:(1)由图可知,
表中自变量是h,因变量是t,
当h=0时,t=20,
故答案为:h,t,20;
(2)设h=kt+b,
,得
即h与t关系是:h=;
(3)当h=6时,6=,
解得,t=﹣16,
即距离地面6千米的高空温度是﹣16℃.
16.解:(1)上述表格反映了弹簧的长度ycm与所挂物体的质量xkg这两个变量之间的关系.其中所挂物体的质量xkg是自变量,弹簧的长度ycm是因变量.
(2)设弹簧长度y(cm)与所挂物体质量x(kg)的关系式为y=kx+b,
将x=0,y=18;x=1,y=20代入得:
k=2,b=18,
∴y=2x+18.
(3)当x=3时,y=24;当x=0时,y=18.
所以,当所挂重物为3kg时,弹簧有24cm长;不挂重物时,弹簧有18cm长.
(4)把y=30代入y=2x+18,
得出:x=6,
所以,弹簧的长度为主30cm时,此时所挂重物的质量是6kg.
17.解:(1)根据题意得:小丽家该月应交煤气费为0.8×50+1.2×(80﹣50)=76(元);
(2)当x≤50时,y=0.8x;
当x>50时,y=0.8×50+1.2(x﹣50)=1.2x﹣20;
(3)设小丽家4月份用煤气x立方米,
∵0.8×50=40(元),而88元>40元,
根据题意得:1.2x﹣20=88,
解得:x=90,
答:小丽家4月份用煤气90立方米;
(4)设6月份小丽家用了a立方米的煤气,
根据题意得:1.2a﹣20=0.95a,
解得:a=80,
答:6月份小丽家用了80立方米的煤气.
18.解:(1)根据图象,学校的纵坐标为1500,小明家的纵坐标为0,
故小明家到学校的路程是1500米;
(2)根据图象,12≤x≤14时,直线最陡,
故小明在12﹣14分钟最快,速度为=450米/分.
(3)根据题意,小明在书店停留的时间为从8分到12分,
故小明在书店停留了4分钟.
(4)读图可得:小明共行驶了1200+600+900=2700米,共用了14分钟.
19.解:(1)快车的速度为300÷=45km/h,慢车的速度为300÷10=30km/h,
故答案为:45,30;
(2)=4h
答:经过4h两车第一次相遇;
(3)(10﹣)×30=100km,
答:当快车到达目的地时,慢车距离目的地100km.
20.解:(1)该车平均每千米的耗油量为(45﹣30)÷150=0.1(L/km),
行驶路程x(km)与剩余油量Q(L)的关系式为Q=45﹣0.1x.
(2)当x=280时,Q=45﹣0.1×280=17.
故当x=280时,剩余油量Q为17L.
故答案为:(1)Q=45﹣0.1x.(2)当x=280时,剩余油量Q为17L
1.已知食用油的沸点一般都在200℃以上,下表所示的是小林加热食用油的过程中,几次测量食用油温度的情况:
时间t/s 0 10 20 30 40
油温y/℃ 10 30 50 70 90
则下列说法不正确的是( )
A.没有加热时,油的温度是10℃
B.继续加热到50s,预计油的温度是110℃
C.每加热10s,油的温度升高30℃
D.在这个问题中,自变量为时间t
2.以下四种情境分别描述了两个变量之间的关系:甲:小明投篮时,投出去的篮球的高度与时间的关系;乙:小明去水果店购买同单价的水果,支付费用与水果重量的关系;丙:小明使用的是一种有月租且只包含流量的套餐,则他每月所付话费与通话时间的关系;丁:小明去外婆家吃饭,饭后,按原速度原路返回,小明离家的距离与时间的关系,如图,用图象法刻画上述情境,排序正确的图象顺序是( )
A.①②③④ B.①③④② C.①③②④ D.①④②③
3.如图,反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,热后回家,其中x表示时间,y表示小明离家的距离,小明家、食堂,图书馆在同一直线上,根据图中提供的信息,有下列说法,其中不正确的是( )
A.食堂离小明家0.4km B.小明从食堂到图书馆用了3min
C.图书馆在小明家和食堂之间 D.小明从图书馆回家的平均速度是0.04km/min
4.向高为10厘米的容器中注水,注满为止,若注水量V(cm3)与水深h(cm)之间的关系的图象大致如图所示,则这个容器是下列四个图中的( )
A. B. C. D.
5.为积极响应党和国家精准扶贫的号召,某扶贫工作队步行前往扶贫点开展入户调查.队员们先匀速步行一段时间,途中休息几分钟后加快了步行速度,最终按原计划时间到达目的地.设行进时间为t(单位:min),行进的路程为x(单位:m),则能近似刻画s与t之间的函数关系的大致图象是( )
A. B.
C. D.
6.在弹簧限度内,弹簧挂上物体后弹簧的长度与所挂物体的质量之间的关系如表:
所挂物体的质量/kg 0 1 2 3 4 5 6 7 8
弹簧的长度/cm 12 12.5 13 13.5 14 14.5 15 15.5 16
在弹簧限度内,弹黄的长度是13cm时,所挂重物的质量是 kg.
7.一辆汽车油箱中现存油50L,汽车每行驶100km耗油10L,则油箱剩余油量y(L)与汽车行驶路程x(km)之间的关系式是 .
8.如图所示的折线ABC为某地向香港地区打电话需付的通话费y(元)与通话时间t(min)之间的函数关系,则通话8min应付通话费 元.
9.为鼓励节约用水,某市规定:每月每户用水不超过10m3,按每立方米1.5元收取水费;若每月每户用水超过10m3,则超过部分每立方米另加收0.5元.设每月每户的用水量为x(m3),应交水费为y(元),试写出当用水量超过10m3时,水费y(元)与用水量x(m3)之间的函数表达式: .若某户某月交水费25元,则该用户当月用水 m3.
10.为了解某品牌轿车的耗油情况,将油箱加满后进行了耗油试验,得到如表数据:
轿车行驶的路程s(km) 0 10 20 30 40 …
油箱剩余油量w(L) 50 49.2 48.4 47.6 46.8 …
(1)在这个变化过程中,自变量是 ,因变量是 ;
(2)该轿车油箱的容量为 L,行驶50km时,油箱剩余油量为 L.
(3)根据如表的数据,写出油箱剩余油量w(L)与轿车行驶的路程s(km)之间的表达式 .
11.如图表示的是汽车在行驶的过程中,速度随时间变化而变化的情况.
(1)汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?
(2)汽车在哪些时间段保持匀速行驶?时速分别是多少?
(3)出发后8分到10分之间可能发生了什么情况?
(4)求汽车从出发后第18分钟到第22分钟行驶的路程.
12.小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与离家距离的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是 米.
(2)小明在书店停留了 分钟.
(3)本次上学途中,小明一共行驶了 米.一共用了 分钟.
(4)在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是速度是多少米/分?
13.小明某天离家,先在A处办事后,再到B处购物,购物后回家.下图描述了他离家的距离s(米)与离家后的时间t(分钟)之间的函数关系,请根据图象回答下列问题:
(1)A处与小明家的距离是 米,小明在从家到A处过程中的速度是 米/分;
(2)小明在B处购物所用的时间是 分钟,他从B处回家过程中的速度是 米/分;
(3)如果小明家、A处和B处在一条直线上,那么小明从离家到回家这一过程(包括停留时间)的平均速度是 米/分.
14.小明家所在地的供电公司实行“峰谷电价”,峰时(8:00~21:00)电价为0.5元/度,谷时(21:00~8:00)电价为0.3元/度.为了解空调制暖的耗能情况,小明记录了家里某天0时~24时内空调制暖的用电量,其用电量y(度)与时间x(h)的函数关系如图所示.
(1)小明家白天不开空调的时间共 h;
(2)求小明家该天空调制暖所用的电费;
(3)设空调制暖所用电费为w元,请画出该天0时~24时内w与x的函数图象.(标注必要数据)
15.父亲告诉小明:“距离地面越高,温度越低”,并给小明出示了下面的表格:
距离地面高度(千米)h 0 1 2 3 4 5
温度(℃)t 20 14 8 2 ﹣4 ﹣10
根据表中,父亲还给小明出了下面几个问题,你和小明一起回答.
(1)表中自变量是 ;因变量是 ;当地面上(即h=0时)时,温度是 ℃.
(2)如果用h表示距离地面的高度,用t表示温度,请写出满足h与t关系的式子.
(3)计算出距离地面6千米的高空温度是多少?
16.在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下表是测得的弹簧的长度y与所挂物体的质量x的几组对应值.
所挂物体质量x/kg 0 1 2 3 4 5
弹簧长度y/cm 18 20 22 24 26 28
(1)上述表格反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)写出弹簧长度y(cm)与所挂物体质量x(kg)的关系式.
(3)当所挂重物为3kg时,弹簧有多长?不挂重物呢?
(4)若弹簧的长度为30cm时,此时所挂重物的质量是多少?(在弹簧的允许范围内).
17.某城市为了加强公民的节气和用气意识,按以下规定收取每月煤气费:所用煤气如果不超过50立方米,按每立方米0.8元收费;如果超过50立方米,超过部分按每立方米1.2元收费.设小丽家每月用气量为x立方米,应交煤气费为y元.
(1)若小丽家某月用煤气量为80立方米,则小丽家该月应交煤气费多少元?
(2)试写出y与x之间的表达式;
(3)若小丽家4月份的煤气费为88元,那么她家4月份所用煤气为多少立方米?
(4)已知小丽家6月份的煤气费平均每立方米0.95元,那么6月份小丽家用了多少立方米的煤气?
18.小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米/分?
(3)小明在书店停留了多少分钟?
(4)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
19.一列快车、一列慢车同时从相距300km的两地出发,相向而行.如图,l1和l2分别表示两车到甲地的距离s(km)与行驶时间t(h)的关系.
(1)快车的速度为 km/h,慢车的速度为 km/h;
(2)经过多久两车第一次相遇?
(3)当快车到达目的地时,慢车距离目的地多远?
20.“十一”期间,小明和父母一起开车到距家200km的景点旅游,出发前,汽车油箱内储油45L,当行驶150km时,发现油箱余油量为30L.(假设行驶过程中汽车的耗油量是均匀的)
(1)求该车平均每千米的耗油量,并写出行驶路程x(km)与剩余油量Q(L)的关系式;
(2)当x=280时,求剩余油量Q.
参考答案
1.解:从表格可知:t=0时,y=10,即没有加热时,油的温度为10℃;
每增加10秒,温度上升20℃,则50秒时,油温度110℃;
110秒时,温度230℃;
在这个问题中,自变量为时间t.
故选:C.
2.解:①篮球运动员投篮时,抛出去的篮的高度变大后逐渐变小至0;
②小明去水果店购买同单价的水果,所付费用与水果重量成正比例关系;
③小明使用的是一种有月租且只包含流量的套餐,他每月所付话费与通话时间的关系是一次函数关系;
④小明去外婆家吃饭,小亮离家的距离从0开始变大,到达外婆家吃饭的时候与家的距离不变,返回时与家的距离变小直至为0.
故顺序为①④②③.
故选:D.
3.解:由纵坐标看出:家到食堂的距离是0.6km,故A不正确,符合题意;
由横坐标看出:小明从食堂到图书馆用了28﹣25=3(min),故B正确,不符合题意;
∵家到食堂的距离是0.6km,家到图书馆的距离是0.4km,0.6cm>0.4cm,
∴图书馆在小明家和食堂之间,
故C正确,不符合题意;
小明从图书馆回家所用的时间为:68﹣58=10(min),
∴小明从图书馆回家的平均速度是:0.4÷10=0.04(km/min),
故D正确,不符合题意;
故选:A.
4.解:根据函数图象可知,注水量V(cm3)与水深h(cm)之间的关系是注水量V(cm3)随着h的增大而增加的速度逐渐减慢,可以得出开始容器由大逐渐变小,即开口越来越小,从图形容器可以看出C符合,
故选:C.
5.解:根据题意得:扶贫工作队行刚开始步行的过程,路程缓慢增加;
途中休息几分钟的过程,路程不变;
加快了步行速度的过程,路程快速增加;
综上可得A选项的函数图象符合.
故选:A.
二.填空题(共4小题)
6.解:从表格中找到当弹簧的长度是13cm时,所挂物体的质量为2kg.
故答案为:2.
7.解:∵汽车每行驶100km耗油10L,
∴汽车行驶路程xkm耗油0.1xL,
∵汽车油箱中现存油50L,
∴油箱剩余油量y(L)与汽车行驶路程x(km)之间的关系式是y=﹣0.1x+50.
故答案是:y=﹣0.1x+50.
8.解:由图象可得,点B(3,2.4),C(5,4.4),
设射线BC的解析式为y=kt+b(t≥3),
则,
解得:,
所以,射线BC的解析式为y=t﹣0.6(t≥3),
当t=8时,y=8﹣0.6=7.4(元),
故答案为:7.4.
9.解:y=1.5×10+(1.5+0.5)(x﹣10)
=2x﹣5,
∵25>1.5×10,
∴用水量超过10m3,
当y=25时,即25=2x﹣5,
解得x=15,
故答案为:y=2x﹣5,15.
三.解答题(共5小题)
10.解;(1)由题意可得,自变量为s,因变量为w;
故答案为:s,w;
(2)根据题意,∵当s=0时,邮箱剩余油量为50L,
∴该轿车邮箱的容量为50L,
∵10公里耗油为0.8L,
∴50公里耗油为4L,
∴行驶50km时,油箱剩余油量为46L;
故答案为:50,46;
(3)设油箱剩余油量w(L)与轿车行驶的路程s(km)之间的表达式为w=ks+b,
把把(0,50)和(10,49.2)代入上式,
得,
解得,
∴油箱剩余油量w(L)与轿车行驶的路程s(km)之间的表达式为w=﹣.
故答案为:w=﹣.
11.解:(1)汽车从出发到最后停止共经过了24min,它的最高时速是75km/h;
(2)汽车在2min到6min,18min到22min保持匀速行驶,时速分别是25km/h和75km/h;
(3)汽车出发8min到10min之间处于静止状态,可能是遇到红灯等情况;
(4)汽车从出发后第18分钟到第22分钟行驶的路程=75×=5(km).
12.解:根据小明本次上学所用的时间与离家距离的关系示意图可知:
(1)小明家到学校的路程是1500米;
故答案为:1500.
(2)小明在书店停留了12﹣8=4(分钟);
故答案为:4.
(3)本次上学途中,小明一共行驶了1200+600+(1500﹣600)=2700(米),一共用了14分钟;
故答案为:2700;14.
(4)在整个上学的途中12分钟至14分钟小明骑车速度最快,最快的速度为:(米/分);
∴在整个上学的途中12分钟至14分钟小明骑车速度最快,最快的速度为:450米/分.
13.解:(1)由图可知,x=5时小明到达A处,A处离家距离为200米;
200÷5=40(米/分).
(2)10﹣5=5(分);
800÷(25﹣20)=160(米/分).
(3)小明往返所走路程为800×2=1600(米),往返所用时间为25分.
∴1600÷25=64(米/分).
故答案为:(1)200,40;
(2)5,160;
(3)64.
14.解:(1)小明家白天不开空调的时间为:18﹣8=10(h),
故答案为:10;
(2)峰时所用电费为:3×3×0.5=4.5(元),
谷时所用电费为:11×3×0.3=9.9(元),
所以小明家该天空调制暖所用的电费为:4.5+9.9=14.4(元);
(3)根据题意,可得该天0时~24时内w与x的函数图象如下:
15.解:(1)由图可知,
表中自变量是h,因变量是t,
当h=0时,t=20,
故答案为:h,t,20;
(2)设h=kt+b,
,得
即h与t关系是:h=;
(3)当h=6时,6=,
解得,t=﹣16,
即距离地面6千米的高空温度是﹣16℃.
16.解:(1)上述表格反映了弹簧的长度ycm与所挂物体的质量xkg这两个变量之间的关系.其中所挂物体的质量xkg是自变量,弹簧的长度ycm是因变量.
(2)设弹簧长度y(cm)与所挂物体质量x(kg)的关系式为y=kx+b,
将x=0,y=18;x=1,y=20代入得:
k=2,b=18,
∴y=2x+18.
(3)当x=3时,y=24;当x=0时,y=18.
所以,当所挂重物为3kg时,弹簧有24cm长;不挂重物时,弹簧有18cm长.
(4)把y=30代入y=2x+18,
得出:x=6,
所以,弹簧的长度为主30cm时,此时所挂重物的质量是6kg.
17.解:(1)根据题意得:小丽家该月应交煤气费为0.8×50+1.2×(80﹣50)=76(元);
(2)当x≤50时,y=0.8x;
当x>50时,y=0.8×50+1.2(x﹣50)=1.2x﹣20;
(3)设小丽家4月份用煤气x立方米,
∵0.8×50=40(元),而88元>40元,
根据题意得:1.2x﹣20=88,
解得:x=90,
答:小丽家4月份用煤气90立方米;
(4)设6月份小丽家用了a立方米的煤气,
根据题意得:1.2a﹣20=0.95a,
解得:a=80,
答:6月份小丽家用了80立方米的煤气.
18.解:(1)根据图象,学校的纵坐标为1500,小明家的纵坐标为0,
故小明家到学校的路程是1500米;
(2)根据图象,12≤x≤14时,直线最陡,
故小明在12﹣14分钟最快,速度为=450米/分.
(3)根据题意,小明在书店停留的时间为从8分到12分,
故小明在书店停留了4分钟.
(4)读图可得:小明共行驶了1200+600+900=2700米,共用了14分钟.
19.解:(1)快车的速度为300÷=45km/h,慢车的速度为300÷10=30km/h,
故答案为:45,30;
(2)=4h
答:经过4h两车第一次相遇;
(3)(10﹣)×30=100km,
答:当快车到达目的地时,慢车距离目的地100km.
20.解:(1)该车平均每千米的耗油量为(45﹣30)÷150=0.1(L/km),
行驶路程x(km)与剩余油量Q(L)的关系式为Q=45﹣0.1x.
(2)当x=280时,Q=45﹣0.1×280=17.
故当x=280时,剩余油量Q为17L.
故答案为:(1)Q=45﹣0.1x.(2)当x=280时,剩余油量Q为17L
同课章节目录
