期末试卷-2020-2021学年高一数学下学期期末专项复习(人教A版必修3+必修4)(含解析)
文档属性
| 名称 | 期末试卷-2020-2021学年高一数学下学期期末专项复习(人教A版必修3+必修4)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-22 23:12:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2020-2021学年高一数学下学期期末复习综合自测
(时间120分钟,满分150分)
选择题(每小题5分,共计60分)
1.已知点在第三象限,则角的终边位置在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.甲、乙两人下棋,甲获胜的概率为,甲不输的概率为,则甲、乙两人下成和棋的概率为( )
A. B. C. D.
3. 在上,满足的的取值范围是( )
A. B.
C. D.
4.已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为( )
A. B. C. D.
5.在△ABC中,N是AC边上一点,且=,P是BN上的一点,若=m+,则实数m的值为( )21·世纪*教育网
A. B. C.1 D.3
6.随机调查某校50个学生的午餐费,结果如下表,这50个学生午餐费的平均值和方差分别是( )
餐费元 3 4 5
人数 10 20 20
A.4, B.4, C., D.,
7. 若,均为锐角,,,则(????)
A. B. C.或 D.
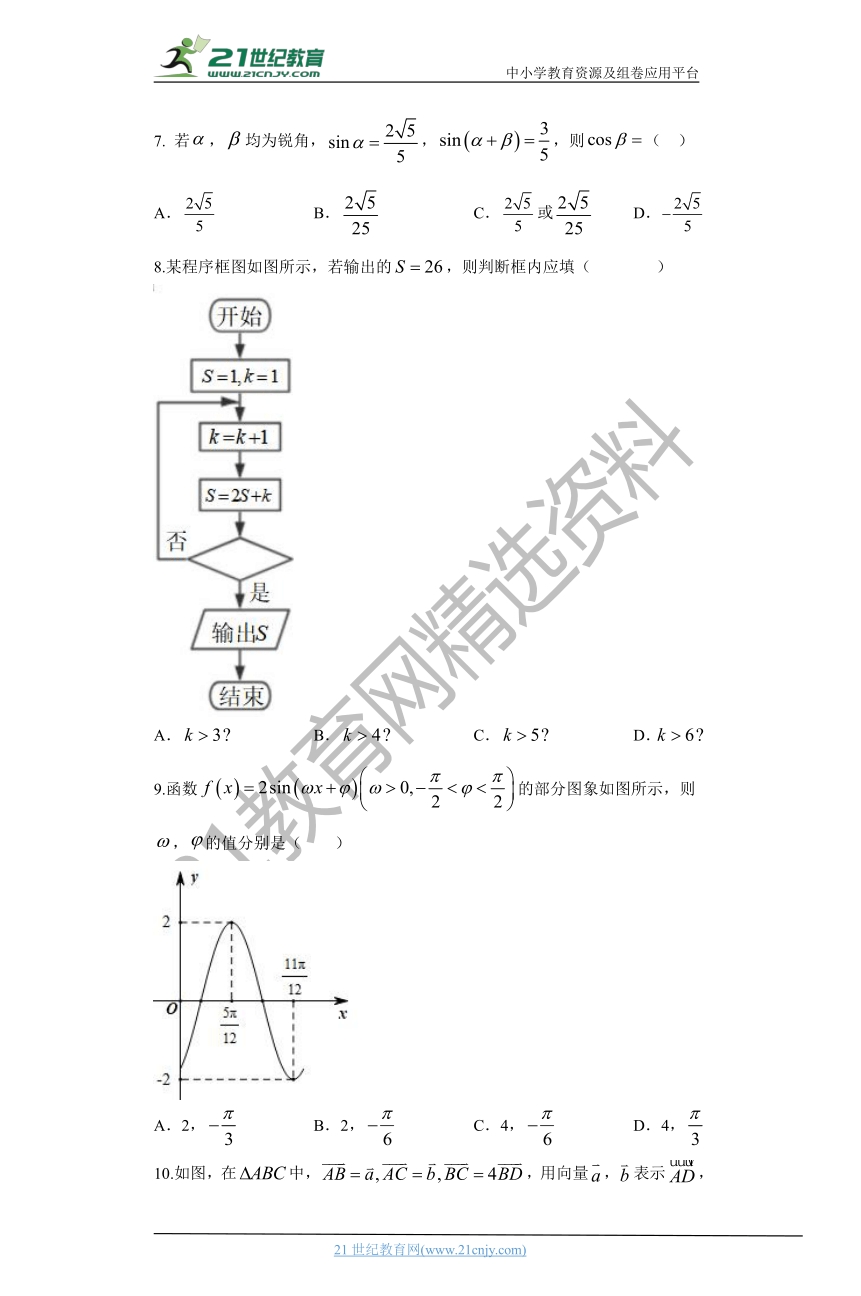
8.某程序框图如图所示,若输出的,则判断框内应填( )
A. B. C. D.
9.函数的部分图象如图所示,则,的值分别是( )
A.2, B.2, C.4, D.4,
10.如图,在中,,用向量,表示,正确的是( )
A. B.
C. D.
11.将函数的图像向右平移个单位长度,所得图像对应的函数恰为偶函数,则的最小值为( )
A. B. C. D.
12.已知平面区域,直线和曲线有两个不的交点,它们围成的平面区域为,向区域?上随机投一点 ,点落在区域内的概率为.若,则的取值范围为( )21cnjy.com
A. B. C. D.
二、填空题(每小题5分,共计20分)
13.若数据的平均数为,则____________.
14. 执行如图所示的程序框图,则输出的k值是________.
15.化简为_____
16.已知,与的夹角为,那么=___________ .
三、解答题(共计70分)
17. (8分)已知函数.
(Ⅰ)化简;
(Ⅱ)若,求的值.
18. (8分)已知向量.
(1)若,求的值;
(2)当时,求与夹角的余弦值.
19. (12分)已知向量,,其中,且.
(1)求和的值;
(2)若,且,求角.
20. (12分)某校从参加高二年级期末考试的学生中抽出60名学生,并统计了他们的化学成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段,,…,后画出如图部分频率分布直方图.观察图形的信息,回答下列问题:【来源:21·世纪·教育·网】
(1)求出这60名学生中化学成绩低于50分的人数;
(2)估计高二年级这次考试化学学科及格率(60分以上为及格);
(3)从化学成绩不及格的学生中随机调查1人,求他的成绩低于50分的概率.
21. (15分)已知向量a=(cos2ωx-sin2ωx,sinωx),b=(,2cosωx),设函数f(x)=a·b(x∈R)的图象关于直线x=对称,其中ω为常数,且ω∈(0,1).
(1)求函数f(x)的最小正周期和单调递增区间;
(2)若将y=f(x)图象上各点的横坐标变为原来的,再将所得图象向右平移个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在上有且只有一个实数解,求实数k的取值范围.www-2-1-cnjy-com
22.(15分)某地随着经济的发展,居民收入逐年增长,如表是该地一建设银行连续五年的储蓄存款(年底余额),如表121世纪教育网版权所有
年份x 2011 2012 2013 2014 2015
储蓄存款y(千亿元) 5 6 7 8 10
为了研究计算的方便,工作人员将上表的数据进行了处理,得到表2:
时间代号t 1 2 3 4 5
z 0 1 2 3 5
(1)求z关于t的线性回归方程;
(2)通过(1)中的方程,求出y关于x的回归方程;
(3)用所求回归方程预测到2010年年底,该地储蓄存款额可达多少?
附:对于线性回归方程,
其中, .
参考答案
1.【答案】B
【分析】判断出的符号,由此判断角的终边位置在象限.
【详解】由于点在第三象限,所以,
所以在第二象限.故选:B
2.【答案】D
【分析】利用互斥事件概率加法公式直接求解.
【详解】甲、乙两人下棋,甲获胜的概率为,甲不输的概率为,
则甲、乙下成平局的概率为:.故选:D.
【点睛】本题考查概率的求法,考查互斥事件概率加法公式等基础知识,属于基础题.
3. 【答案】B
【分析】根据的函数图象结合特殊角的三角函数值,即可容易求得结果.
【详解】根据的图象可知:当时,或,
数形结合可知:当,得.故选:.
【点睛】本题考查利用三角函数的图象解不等式,属简单题.
4. 【答案】C
【分析】设回归直线方程为,根据回归直线必过样本中心,求.
【详解】由回归直线的斜率的估计值为1.23,设回归直线方程为,
代入 , ,解得: ,回归直线方程是.
故选:C
【点睛】本题考查回归直线方程,意在考查基本公式和计算,属于简单题型.
5. 【答案】 B
【分析】根据向量的线性表示逐步代换掉不需要的向量求解.
【详解】设 ,
所以 所以 故选B.
【点睛】本题考查向量的线性运算,属于基础题.
6. 【答案】C
【分析】根据题目中的数据,求出它们的平均数和方差即可.
【详解】根据题意,得这50个学生午餐费的平均值是:
,
方差是:,故选C.
【点睛】该题考查的是有关求一组数据的平均数和方差的问题,涉及到的知识点有平均数和方差的公式,属于简单题目.21教育网
7. 【答案】B
【分析】首先判断的范围,再表示为,利用两角差的余弦公式求解.
【详解】因为,均为锐角,若是锐角,那么,则,这与已知矛盾,所以是钝角,则
,
.故选:B
【点睛】本题考查已知三角函数求值,重点考查角的转化,属于基础题型,本题的易错点是忽略判断的范围,而造成增根情况.21·cn·jy·com
8. 【答案】A
【分析】根据程序框图的结构及输出结果,逆向推断即可得判断框中的内容.
【详解】由程序框图可知,,则
所以此时输出的值,因而时退出循环.因而判断框的内容为故选:A
【点睛】本题考查了根据程序框图的输出值,确定判断框的内容,属于基础题.
9. 【答案】A
【分析】利用正弦函数的周期性可得,进而求得,再利用时取得最大值可求得值.
【详解】∵在同一周期内,函数在时取得最大值,时取得最小值,
∴函数的周期满足,由此可得,解得,
函数表达式为.又∵当时取得最大值2,
∴,可得,∵,
∴取,得.故选:A.
【点睛】本题考查由的部分图象确定函数解析式,考查正弦函数的周期性和最值,属于基础题.
10. 【答案】C
【分析】由得,再由向量的加法得,最后把代入,求得答案.
【详解】因为,故选C.
【点睛】本题考查向量的加法和数乘运算的几何意义,考查平面向量基本定理在图形中的应用.
11. 【答案】D
【分析】本题首先可根据诱导公式以及二倍角公式将函数转化为,然后根据三角函数平移的相关性质得出平移后的函数为,最后根据函数为偶函数即可得出结果.
【详解】令,
则
,
设向右平移个单位长度后得到的函数为,
则,
因为函数为偶函数,所以,解得,
因为,所以的最小值为,故选:D.
【点睛】本题考查诱导公式、二倍角公式、三角函数图像的平移以及三角函数的奇偶性,考查的公式有、,考查计算能力,考查化归与转化思想,是中档题.www.21-cn-jy.com
12. 【答案】D
【分析】判断平面区域,利用特殊值法排除选项,然后利用特殊法,即可求解相应概率的范围,得到答案.
【详解】由题意知,平面区域,表示的图形是半圆是半圆以及内部点的集合,如图所示,又由直线过半圆上一点,2-1-c-n-j-y
当时直线与轴重合,此时,故可排除,
若,如图所示,可求得,所以的取值范围为.
【点睛】本题主要考查了集合概型的_?????¨?????????è§?_答中判断平面区域,利用特殊值法排除选项,然后利用特殊法,求解相应概率的范围是解答的关键,着重考查了分析问题和解答问题的能力,属于中档试题.21*cnjy*com
13. 【答案】
【分析】根据求平均数的公式,得到关于的方程,求得.
【详解】由题意得:,解得:,故填:.
【点睛】本题考查求一组数据的平均数,考查基本数据处理能力.
14. 【答案】3
【解析】试题分析:由程序框图知,输出.
考点:程序框图.
15. 【答案】1
【分析】根据同角三角函数的基本关系式对所求表达式进行化简,由此求得表达式的值.
【详解】
依题意.
【点睛】本小题主要考查同角三角函数的基本关系式,考查化归与转化的数学思想方法,属于基础题.
16. 【答案】
【分析】由,与的夹角为,求出与的数量积,然后直接利用向量的模的求法,求出的值即可.
【详解】与的夹角为,
,
,
,故答案为.
【点睛】本题主要考查向量的模及平面向量数量积公式,属于中档题.平面向量数量积公式有两种形式,一是,二是,主要应用以下几个方面:(1)求向量的夹角, (此时往往用坐标形式求解);(2)求投影, 在 上的投影是;(3)向量垂直则;(4)求向量 的模(平方后需求).【来源:21cnj*y.co*m】
17. 【答案】 (1);(2)
【分析】
(1)根据诱导公式化简分子、分母,即可得,进而可得最简形式;(2)根据两角和的正切公式有,结合已知求得,即可求函数值2·1·c·n·j·y
【详解】
(1),
∴
∴
(2)由,知:,即
又,所以
【点睛】本题考查了利用诱导公式化简函数式,并由已知函数值,结合两角和的正切公式求函数值,属于简单题
18. 【答案】(1)-3;(2)-.
【分析】
(1)根据向量平行的坐标关系求得
(2)根据向量的数量积运算求得夹角.
【详解】 (1)由题意,得.因为,
所以,解得.
(2)当时,.
设与的夹角为θ,则
.
所以与夹角的余弦值为-.
【点睛】本题考查向量的平行关系和向量数量积运算,属于基础题.
19. 【答案】 (1),;(2).
【详解】
(1)∵,∴,即.
代入,得,
又,则,.
则.
.
(2)∵,,∴.
又,∴.
∴==.
由,得.
20. 【答案】(1)6人;(2)75%;(3).
【解析】
试题分析:(1)由频率分布直方图可得化学成绩低于50分的频率为0.1,然后可求得人数为人;(2)根据频率分布直方图求分数在第三、四、五、六组的频率之和即可;(3)结合图形可得“成绩低于50分”的人数是6人,成绩在这组的人数是,由古典概型概率公式可得所求概率为.
试题解析:
(1)因为各组的频率和等于1,由频率分布直方图可得低于50分的频率为:
,
所以低于分的人数为(人).
(2)依题意可得成绩60及以上的分数所在的第三、四、五、六组(低于50分的为第一组),其频率之和为,
故抽样学生成绩的及格率是,
于是,可以估计这次考试化学学科及格率约为75%.
(3)由(1)知,“成绩低于50分”的人数是6人,
成绩在这组的人数是(人),
所以从成绩不及格的学生中随机调查1人,有15种选法,成绩低于50分有6种选法,
故所求概率为.
21. 【答案】(1)T=6π;单调递增区间为,k∈Z.(2){k|或k=-2}.
【分析】
(1)先利用平面向量的数量积定义和二倍角公式、辅助角公式得到,再利用对称性求出值,再利用三角函数的性质进行求解;(2)先利用三角函数图象变换得到,再令,利用三角函数的图象和数形结合思想进行求解.【出处:21教育名师】
【详解】
(1)f(x)=a·b=(cos2ωx-sin2ωx)+2sinωxcosωx
=cos2ωx+sin2ωx=2sin.
∵直线x=是y=f(x)的图象的一条对称轴,
∴(k∈Z),即ω=k+(k∈Z).
又ω∈(0,1),∴ω=,f(x)=2sin,
∴T=6π.
令,k∈Z,得,k∈Z,
即函数f(x)的单调递增区间为,k∈Z.
(2)由(1)得f(x)=2sin,将y=f(x)图象上各点的横坐标变为原来的,再将所得图象向右平移个单位,纵坐标不变,得到y=2sin的图象,∴h(x)=2sin.【版权所有:21教育】
令=t,∵0≤x≤,∴-≤t≤,
方程h(x)+k=0在上有且只有一个实数解,
即方程2sint+k=0在上有且只有一个实数解,
亦即y=2sint,t∈的图象与直线y=-k有且只有一个交点,
画出图象分析可知-≤-k<或-k=2,即或k=-2.
故实数k的取值范围是{k|或k=-2}.
【点睛】本题主要考查三角恒等变换、三角函数的图象和性质、三角函数的图象变换,意在考查学生的逻辑思维能力和综合分析解决问题的能力,属于中档题.解决本题的易错点在于三角函数的图象变换,学生往往得到错误的结果“”,在处理图象平移时,要注意平移的单位仅对于“自变量”而言,如本题中.21教育名师原创作品
22.【答案】(1);(2);(3)3.6千亿.
【解析】
【分析】
(1)利用最小二乘法求出z关于t的线性回归方程;
(2)通过,把z关于t的线性回归方程化成y关于x的回归方程;
(3)利用回归方程代入求值.
【详解】
解:(1)由表中数据,计算(1+2+3+4+5)=3,
(0+1+2+3+5)=2.2,
tizi=1×0+2×1+3×2+4×3+5×5=45,
12+22+32+42+52=55,
所以1.2,
b2.2﹣1.2×3=﹣1.4,
所以z关于t的线性回归方程为z=1.2t﹣1.4;
(2)把t=x﹣2010,z=y﹣5代入z=1.2t﹣1.4中,得到:
y﹣5=1.2(x﹣2010)﹣1.4,
即y关于x的回归方程是y=1.2x﹣2408.4;
(3)由(2)知,计算x=2010时,y=1.2×2010﹣2408.4=3.6,
即预测到2010年年底,该地储蓄存款额可达3.6千亿.
【点睛】本题主要考查了非线性回归模型问题,采用适当的变量替换,把问题转化成线性回归问题,是求解非线性回归问题的主要手段.
_21?????????è?????(www.21cnjy.com)_
2020-2021学年高一数学下学期期末复习综合自测
(时间120分钟,满分150分)
选择题(每小题5分,共计60分)
1.已知点在第三象限,则角的终边位置在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.甲、乙两人下棋,甲获胜的概率为,甲不输的概率为,则甲、乙两人下成和棋的概率为( )
A. B. C. D.
3. 在上,满足的的取值范围是( )
A. B.
C. D.
4.已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为( )
A. B. C. D.
5.在△ABC中,N是AC边上一点,且=,P是BN上的一点,若=m+,则实数m的值为( )21·世纪*教育网
A. B. C.1 D.3
6.随机调查某校50个学生的午餐费,结果如下表,这50个学生午餐费的平均值和方差分别是( )
餐费元 3 4 5
人数 10 20 20
A.4, B.4, C., D.,
7. 若,均为锐角,,,则(????)
A. B. C.或 D.
8.某程序框图如图所示,若输出的,则判断框内应填( )
A. B. C. D.
9.函数的部分图象如图所示,则,的值分别是( )
A.2, B.2, C.4, D.4,
10.如图,在中,,用向量,表示,正确的是( )
A. B.
C. D.
11.将函数的图像向右平移个单位长度,所得图像对应的函数恰为偶函数,则的最小值为( )
A. B. C. D.
12.已知平面区域,直线和曲线有两个不的交点,它们围成的平面区域为,向区域?上随机投一点 ,点落在区域内的概率为.若,则的取值范围为( )21cnjy.com
A. B. C. D.
二、填空题(每小题5分,共计20分)
13.若数据的平均数为,则____________.
14. 执行如图所示的程序框图,则输出的k值是________.
15.化简为_____
16.已知,与的夹角为,那么=___________ .
三、解答题(共计70分)
17. (8分)已知函数.
(Ⅰ)化简;
(Ⅱ)若,求的值.
18. (8分)已知向量.
(1)若,求的值;
(2)当时,求与夹角的余弦值.
19. (12分)已知向量,,其中,且.
(1)求和的值;
(2)若,且,求角.
20. (12分)某校从参加高二年级期末考试的学生中抽出60名学生,并统计了他们的化学成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段,,…,后画出如图部分频率分布直方图.观察图形的信息,回答下列问题:【来源:21·世纪·教育·网】
(1)求出这60名学生中化学成绩低于50分的人数;
(2)估计高二年级这次考试化学学科及格率(60分以上为及格);
(3)从化学成绩不及格的学生中随机调查1人,求他的成绩低于50分的概率.
21. (15分)已知向量a=(cos2ωx-sin2ωx,sinωx),b=(,2cosωx),设函数f(x)=a·b(x∈R)的图象关于直线x=对称,其中ω为常数,且ω∈(0,1).
(1)求函数f(x)的最小正周期和单调递增区间;
(2)若将y=f(x)图象上各点的横坐标变为原来的,再将所得图象向右平移个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在上有且只有一个实数解,求实数k的取值范围.www-2-1-cnjy-com
22.(15分)某地随着经济的发展,居民收入逐年增长,如表是该地一建设银行连续五年的储蓄存款(年底余额),如表121世纪教育网版权所有
年份x 2011 2012 2013 2014 2015
储蓄存款y(千亿元) 5 6 7 8 10
为了研究计算的方便,工作人员将上表的数据进行了处理,得到表2:
时间代号t 1 2 3 4 5
z 0 1 2 3 5
(1)求z关于t的线性回归方程;
(2)通过(1)中的方程,求出y关于x的回归方程;
(3)用所求回归方程预测到2010年年底,该地储蓄存款额可达多少?
附:对于线性回归方程,
其中, .
参考答案
1.【答案】B
【分析】判断出的符号,由此判断角的终边位置在象限.
【详解】由于点在第三象限,所以,
所以在第二象限.故选:B
2.【答案】D
【分析】利用互斥事件概率加法公式直接求解.
【详解】甲、乙两人下棋,甲获胜的概率为,甲不输的概率为,
则甲、乙下成平局的概率为:.故选:D.
【点睛】本题考查概率的求法,考查互斥事件概率加法公式等基础知识,属于基础题.
3. 【答案】B
【分析】根据的函数图象结合特殊角的三角函数值,即可容易求得结果.
【详解】根据的图象可知:当时,或,
数形结合可知:当,得.故选:.
【点睛】本题考查利用三角函数的图象解不等式,属简单题.
4. 【答案】C
【分析】设回归直线方程为,根据回归直线必过样本中心,求.
【详解】由回归直线的斜率的估计值为1.23,设回归直线方程为,
代入 , ,解得: ,回归直线方程是.
故选:C
【点睛】本题考查回归直线方程,意在考查基本公式和计算,属于简单题型.
5. 【答案】 B
【分析】根据向量的线性表示逐步代换掉不需要的向量求解.
【详解】设 ,
所以 所以 故选B.
【点睛】本题考查向量的线性运算,属于基础题.
6. 【答案】C
【分析】根据题目中的数据,求出它们的平均数和方差即可.
【详解】根据题意,得这50个学生午餐费的平均值是:
,
方差是:,故选C.
【点睛】该题考查的是有关求一组数据的平均数和方差的问题,涉及到的知识点有平均数和方差的公式,属于简单题目.21教育网
7. 【答案】B
【分析】首先判断的范围,再表示为,利用两角差的余弦公式求解.
【详解】因为,均为锐角,若是锐角,那么,则,这与已知矛盾,所以是钝角,则
,
.故选:B
【点睛】本题考查已知三角函数求值,重点考查角的转化,属于基础题型,本题的易错点是忽略判断的范围,而造成增根情况.21·cn·jy·com
8. 【答案】A
【分析】根据程序框图的结构及输出结果,逆向推断即可得判断框中的内容.
【详解】由程序框图可知,,则
所以此时输出的值,因而时退出循环.因而判断框的内容为故选:A
【点睛】本题考查了根据程序框图的输出值,确定判断框的内容,属于基础题.
9. 【答案】A
【分析】利用正弦函数的周期性可得,进而求得,再利用时取得最大值可求得值.
【详解】∵在同一周期内,函数在时取得最大值,时取得最小值,
∴函数的周期满足,由此可得,解得,
函数表达式为.又∵当时取得最大值2,
∴,可得,∵,
∴取,得.故选:A.
【点睛】本题考查由的部分图象确定函数解析式,考查正弦函数的周期性和最值,属于基础题.
10. 【答案】C
【分析】由得,再由向量的加法得,最后把代入,求得答案.
【详解】因为,故选C.
【点睛】本题考查向量的加法和数乘运算的几何意义,考查平面向量基本定理在图形中的应用.
11. 【答案】D
【分析】本题首先可根据诱导公式以及二倍角公式将函数转化为,然后根据三角函数平移的相关性质得出平移后的函数为,最后根据函数为偶函数即可得出结果.
【详解】令,
则
,
设向右平移个单位长度后得到的函数为,
则,
因为函数为偶函数,所以,解得,
因为,所以的最小值为,故选:D.
【点睛】本题考查诱导公式、二倍角公式、三角函数图像的平移以及三角函数的奇偶性,考查的公式有、,考查计算能力,考查化归与转化思想,是中档题.www.21-cn-jy.com
12. 【答案】D
【分析】判断平面区域,利用特殊值法排除选项,然后利用特殊法,即可求解相应概率的范围,得到答案.
【详解】由题意知,平面区域,表示的图形是半圆是半圆以及内部点的集合,如图所示,又由直线过半圆上一点,2-1-c-n-j-y
当时直线与轴重合,此时,故可排除,
若,如图所示,可求得,所以的取值范围为.
【点睛】本题主要考查了集合概型的_?????¨?????????è§?_答中判断平面区域,利用特殊值法排除选项,然后利用特殊法,求解相应概率的范围是解答的关键,着重考查了分析问题和解答问题的能力,属于中档试题.21*cnjy*com
13. 【答案】
【分析】根据求平均数的公式,得到关于的方程,求得.
【详解】由题意得:,解得:,故填:.
【点睛】本题考查求一组数据的平均数,考查基本数据处理能力.
14. 【答案】3
【解析】试题分析:由程序框图知,输出.
考点:程序框图.
15. 【答案】1
【分析】根据同角三角函数的基本关系式对所求表达式进行化简,由此求得表达式的值.
【详解】
依题意.
【点睛】本小题主要考查同角三角函数的基本关系式,考查化归与转化的数学思想方法,属于基础题.
16. 【答案】
【分析】由,与的夹角为,求出与的数量积,然后直接利用向量的模的求法,求出的值即可.
【详解】与的夹角为,
,
,
,故答案为.
【点睛】本题主要考查向量的模及平面向量数量积公式,属于中档题.平面向量数量积公式有两种形式,一是,二是,主要应用以下几个方面:(1)求向量的夹角, (此时往往用坐标形式求解);(2)求投影, 在 上的投影是;(3)向量垂直则;(4)求向量 的模(平方后需求).【来源:21cnj*y.co*m】
17. 【答案】 (1);(2)
【分析】
(1)根据诱导公式化简分子、分母,即可得,进而可得最简形式;(2)根据两角和的正切公式有,结合已知求得,即可求函数值2·1·c·n·j·y
【详解】
(1),
∴
∴
(2)由,知:,即
又,所以
【点睛】本题考查了利用诱导公式化简函数式,并由已知函数值,结合两角和的正切公式求函数值,属于简单题
18. 【答案】(1)-3;(2)-.
【分析】
(1)根据向量平行的坐标关系求得
(2)根据向量的数量积运算求得夹角.
【详解】 (1)由题意,得.因为,
所以,解得.
(2)当时,.
设与的夹角为θ,则
.
所以与夹角的余弦值为-.
【点睛】本题考查向量的平行关系和向量数量积运算,属于基础题.
19. 【答案】 (1),;(2).
【详解】
(1)∵,∴,即.
代入,得,
又,则,.
则.
.
(2)∵,,∴.
又,∴.
∴==.
由,得.
20. 【答案】(1)6人;(2)75%;(3).
【解析】
试题分析:(1)由频率分布直方图可得化学成绩低于50分的频率为0.1,然后可求得人数为人;(2)根据频率分布直方图求分数在第三、四、五、六组的频率之和即可;(3)结合图形可得“成绩低于50分”的人数是6人,成绩在这组的人数是,由古典概型概率公式可得所求概率为.
试题解析:
(1)因为各组的频率和等于1,由频率分布直方图可得低于50分的频率为:
,
所以低于分的人数为(人).
(2)依题意可得成绩60及以上的分数所在的第三、四、五、六组(低于50分的为第一组),其频率之和为,
故抽样学生成绩的及格率是,
于是,可以估计这次考试化学学科及格率约为75%.
(3)由(1)知,“成绩低于50分”的人数是6人,
成绩在这组的人数是(人),
所以从成绩不及格的学生中随机调查1人,有15种选法,成绩低于50分有6种选法,
故所求概率为.
21. 【答案】(1)T=6π;单调递增区间为,k∈Z.(2){k|或k=-2}.
【分析】
(1)先利用平面向量的数量积定义和二倍角公式、辅助角公式得到,再利用对称性求出值,再利用三角函数的性质进行求解;(2)先利用三角函数图象变换得到,再令,利用三角函数的图象和数形结合思想进行求解.【出处:21教育名师】
【详解】
(1)f(x)=a·b=(cos2ωx-sin2ωx)+2sinωxcosωx
=cos2ωx+sin2ωx=2sin.
∵直线x=是y=f(x)的图象的一条对称轴,
∴(k∈Z),即ω=k+(k∈Z).
又ω∈(0,1),∴ω=,f(x)=2sin,
∴T=6π.
令,k∈Z,得,k∈Z,
即函数f(x)的单调递增区间为,k∈Z.
(2)由(1)得f(x)=2sin,将y=f(x)图象上各点的横坐标变为原来的,再将所得图象向右平移个单位,纵坐标不变,得到y=2sin的图象,∴h(x)=2sin.【版权所有:21教育】
令=t,∵0≤x≤,∴-≤t≤,
方程h(x)+k=0在上有且只有一个实数解,
即方程2sint+k=0在上有且只有一个实数解,
亦即y=2sint,t∈的图象与直线y=-k有且只有一个交点,
画出图象分析可知-≤-k<或-k=2,即或k=-2.
故实数k的取值范围是{k|或k=-2}.
【点睛】本题主要考查三角恒等变换、三角函数的图象和性质、三角函数的图象变换,意在考查学生的逻辑思维能力和综合分析解决问题的能力,属于中档题.解决本题的易错点在于三角函数的图象变换,学生往往得到错误的结果“”,在处理图象平移时,要注意平移的单位仅对于“自变量”而言,如本题中.21教育名师原创作品
22.【答案】(1);(2);(3)3.6千亿.
【解析】
【分析】
(1)利用最小二乘法求出z关于t的线性回归方程;
(2)通过,把z关于t的线性回归方程化成y关于x的回归方程;
(3)利用回归方程代入求值.
【详解】
解:(1)由表中数据,计算(1+2+3+4+5)=3,
(0+1+2+3+5)=2.2,
tizi=1×0+2×1+3×2+4×3+5×5=45,
12+22+32+42+52=55,
所以1.2,
b2.2﹣1.2×3=﹣1.4,
所以z关于t的线性回归方程为z=1.2t﹣1.4;
(2)把t=x﹣2010,z=y﹣5代入z=1.2t﹣1.4中,得到:
y﹣5=1.2(x﹣2010)﹣1.4,
即y关于x的回归方程是y=1.2x﹣2408.4;
(3)由(2)知,计算x=2010时,y=1.2×2010﹣2408.4=3.6,
即预测到2010年年底,该地储蓄存款额可达3.6千亿.
【点睛】本题主要考查了非线性回归模型问题,采用适当的变量替换,把问题转化成线性回归问题,是求解非线性回归问题的主要手段.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
