人教A必修3综合测试-2020-2021学年高一数学下学期期末专项复习(人教A版必修3)(含解析)
文档属性
| 名称 | 人教A必修3综合测试-2020-2021学年高一数学下学期期末专项复习(人教A版必修3)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-22 23:15:20 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2020-2021学年高一数学下学期期末复习自测(必修三)
(时间120分钟,满分150分)
选择题(每小题5分,共计60分)
1.半径为的圆的面积公式为,当时,则计算面积的流程图为( )
A.
B.
C.
D.
2.已知一组数据1,2,3,4,5,那么这组数据的方差为( )
A. B.2 C. D.3
3.某地区的高一新生中,来自_???é?¨????????°???_的学生有2400人,中部丘陵地区的学生有1600人,西部山区的学生有1000人.计划从中选取100人调查学生的视力情况,现已了解到来自东部、中部、西部三个地区学生的视力情况有较大差异,而这三个地区男女生视力情况差异不大,在下面的抽样方法中,最合理的抽样方法是( )2·1·c·n·j·y
A.简单随机抽样 B.按性别分层抽样
C.系统抽样 D.按地区分层抽样
4.用秦九韶算法求多项式f(x)=0.5x5+4x4-3x2+x-1当x=3的值时,先算的是( )
A.3×3=9 B.0.5×35=121.5
C.0.5×3+4=5.5 D.(0.5×3+4)×3=16.5
5.为了保障广大人民群众的身体健康,在新冠肺炎疫情防控期间,有关部门对辖区内家药店所销售的、两种型号的口罩进行了抽检,每家药店抽检包口罩(每包只),家药店中抽检的、型号口罩不合格数(Ⅰ、Ⅱ)的茎叶图如图所示,则下列描述不正确的是( )
A.估计型号口罩的合格率小于型号口罩的合格率
B.Ⅰ组数据的众数大于Ⅱ组数据的众数
C.Ⅰ组数据的中位数大于Ⅱ组数据的中位数
D.Ⅰ组数据的方差大于Ⅱ组数据的方差
6.某单位共有名职工,其中不到岁的有人,岁的有人,岁及以上的有人,现用分层抽样的方法,从中抽出名职工了解他们的健康情况.如果已知岁的职工抽取了人,则岁及以上的职工抽取的人数为( )【来源:21cnj*y.co*m】
A. B. C. D.
7.某省在新的高考改革方案中规定:每位考生的高考成绩是按照3(语文、数学、英语)(物理、历史)选(化学、生物、地理、政治)选2的模式设置的,则某考生选择全理科的概率是( )
A. B. C. D.
8.小王因上班繁忙,来不及做午_é?????????????????_外卖.假设小王和外卖小哥都在12:00~12:10之间随机到达小王所居住的楼下,则小王在楼下等候外卖小哥的时间不超过5分钟的概率是( )
A. B. C. D.
9.凤鸣山中学的高中女生体重 (单位:kg)与身高(单位:cm)具有线性相关关系,根据一组样本数据(),用最小二乘法近似得到回归直线方程为,则下列结论中不正确的是( )
A.与具有正线性相关关系
B.回归直线过样本的中心点
C.若该中学某高中女生身高增加1cm,则其体重约增加0.85kg
D.若该中学某高中女生身高为160cm,则可断定其体重必为50.29kg.
10.为了更好地支持“中小型企_?????????????±????_某市决定对部分企业的税收进行适当的减免,某机构调查了当地的中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,下面三个结论:
①样本数据落在区间的频率为0.45;
②如果规定年收入在500万元以内的企业才能享受减免税政策,估计有55%的当地中小型企业能享受到减免税政策;
③样本的中位数为480万元.
其中正确结论的个数为
A.0 B.1 C.2 D.3
11.自然界中具有两种稳定状态的组件普遍存在,如开关的开和关、电路的通和断等,非常适合表示计算机中的数,所以现在使用的计算机设计为二进制.二进制以为基数,只用和两个数表示数,逢进,二进制数与十进制数遵循一样的运算规则,它们可以相互转化,如.我国数学史上,清代汪莱的《参两算经》是较早系统论述非十进制数的文献,总结出了八进制乘法口决:,,,则八进制下等于
A. B. C. D.
12.方程有实根的概率为( )
A. B. C. D.
二、填空题(每小题5分,共计20分)
13.阅读如图所示的程序框图,运行相应的程序,则输出的值为__________.
14.请把6进制数化成8进制数: .
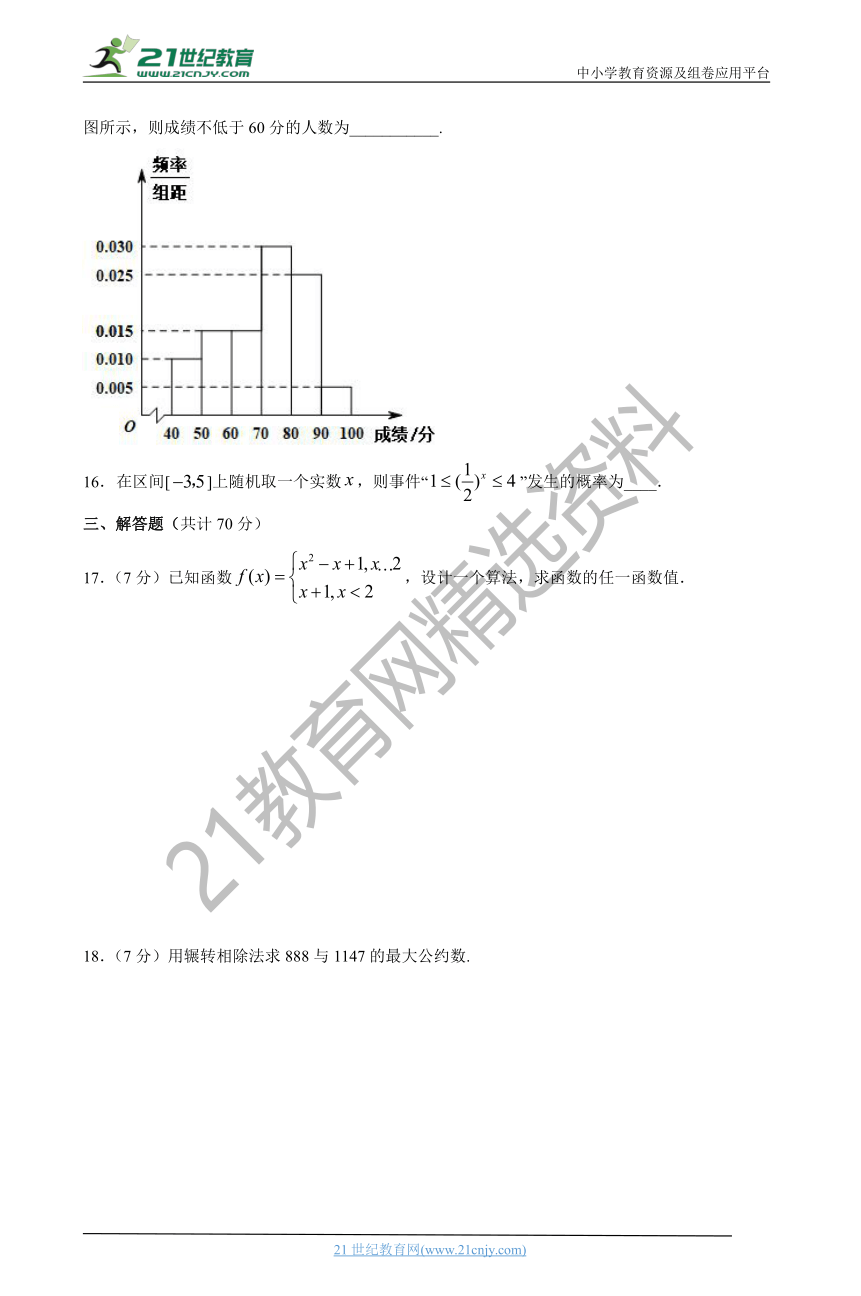
15.某班48名学生参加建国70周年知识竞赛,成绩都在区间,上,其频率分布直方图如图所示,则成绩不低于60分的人数为___________.21*cnjy*com
在区间[]上随机取一个实数,则事件“”发生的概率为____.
三、解答题(共计70分)
17.(7分)已知函数,设计一个算法,求函数的任一函数值.
18.(7分)用辗转相除法求888与1147的最大公约数.
19.(12分) 抛掷两颗骰子,计算:
(1)事件“两颗骰子点数相同”的概率;
(2)事件“点数之和小于7”的概率;
(3)事件“点数之和等于或大于11”的概率.
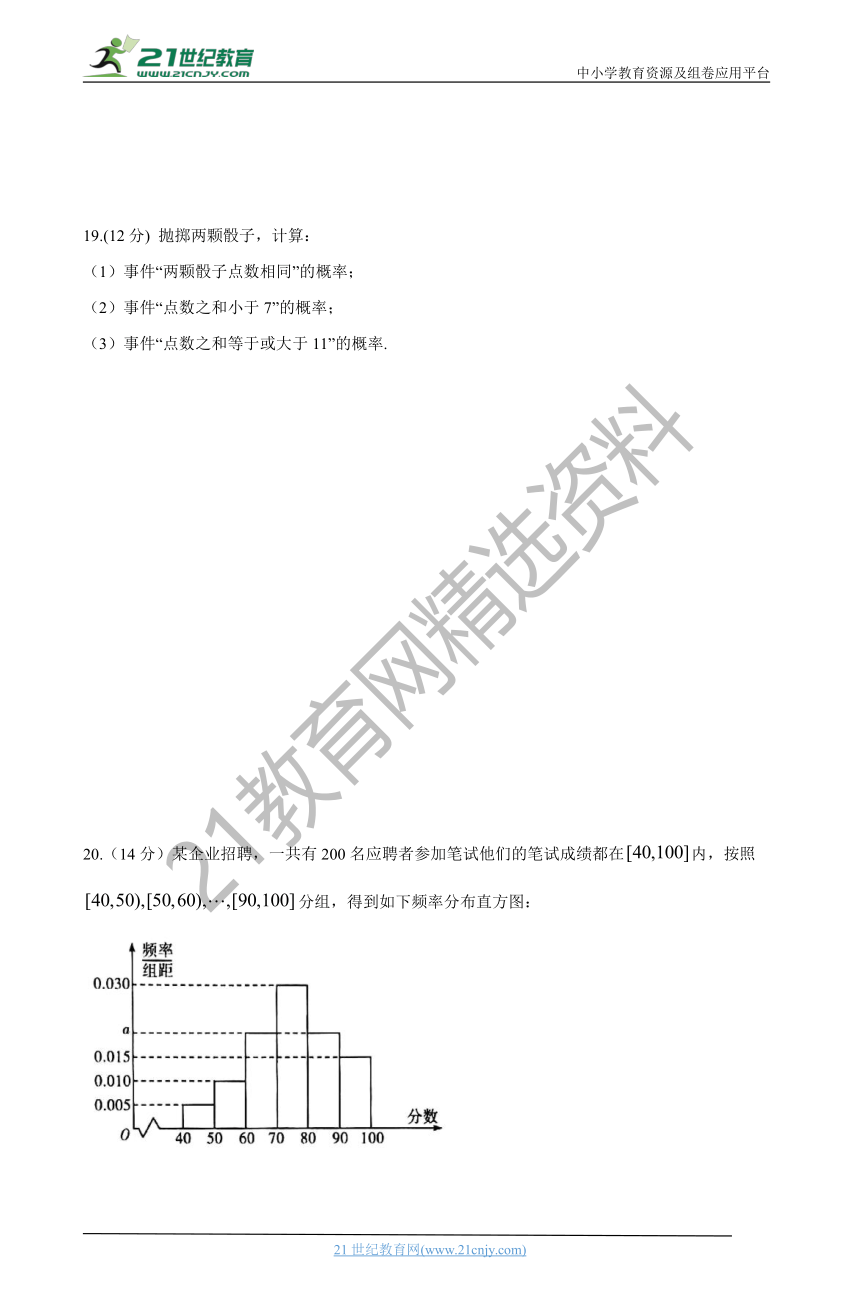
20.(14分)某企业招聘,一共有200名应聘者参加笔试他们的笔试成绩都在内,按照分组,得到如下频率分布直方图:21·世纪*教育网
(Ⅰ)求图中的值;
(Ⅱ)求全体应聘者笔试成绩的平均数;(每组数据以区间中点值为代表)
(Ⅲ)该企业根据笔试成绩从高到低进行录取,若计划录取150人,估计应该把录取的分数线定为多少.
21.(15分)某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段,,,,,,后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:21世纪教育网版权所有
(1)求分数在,内的频率,并补全这个频率分布直方图;
(2)估计本次考试的平均分及中位数;
(3)用分层抽样的方法在分数段为,的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段,内的概率.21教育网
22.(15分_?????°???è????????_情期间,为确保“停课不停学”,各校精心组织了线上教学活动.开学后,某校采用分层抽样的方法从三个年级的学生中抽取一个容量为150的样本进行关于线上教学实施情况的问卷调查.已知该校高一年级共有学生660人,抽取的样本中高二年级有50人,高三年级有45人.下表是根据抽样调查情况得到的高二学生日睡眠时间(单位:h)的频率分布表.
分组 频数 频率
5 0.10
8 0.16
x 0.14
12 y
10 0.20
z
合计 50 1
(1)求该校学生总数;
(2)求频率分布表中实数x,y,z的值;
(3)已知日睡眠时间在区间[_6???6.5)_的5名高二学生中,有2名女生,3名男生,若从中任选2人进行面谈,则选中的2人恰好为一男一女的概率.21·cn·jy·com
参考答案
1.【答案】B
【分析】因为处理输入和输出框是平行四边形,据此即可选出答案.
【详解】输入和输出框是平行四边形,故计算面积的流程图为B.故选:B.
2.【答案】B
【分析】先由平均数的计算公式计算出平均数,再根据方差的公式计算即可.
【详解】由题可得;
所以这组数据的方差 故选:B.
【点睛】本题考查方差的定义:一般地设个数据:的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动越大,方差越小,波动越小.2-1-c-n-j-y
3.【答案】D
【分析】根据抽样方法的特征,即可得出结论.
【详解】由于该地区东部、中部、西部三个地区学生的视力情况有较大差异,故按地区分层抽样.
【点睛】本题主要考查抽样方法,熟记每种抽样方法的特征即可,属于基础题型.
4.【答案】C
【详解】f(x)=((((_0.5x+4_)x+0)x-3)x+1)x-1,按递推方法,从里到外先算0.5x+4的值,将x=3代入求得0.5×3+4=5.5.故选C.【来源:21·世纪·教育·网】
5.【答案】D
【分析】根据茎叶图中的_??°???è??????????¤_种型号口罩的合格率,可判断A选项的正误;求出两组数据的众数,可判断B选项的正误;求出两组数据的中位数,可判断C选项的正误;利用排除法可判断D选项的正误.【出处:21教育名师】
【详解】对于A选项,由茎叶图可知,型号口罩的不合格数为,
型口罩的不合格数为,
型号口罩的合格率为,型口罩的合格率为,
所以,型口罩的合格率小于型口罩的合格率,A选项正确;
对于B选项,Ⅰ组数据的众数为,Ⅱ组数据的众数,B选项正确;
对于C选项,Ⅰ组数据的中位数为,Ⅱ组数据的,C选项正确;
由排除法可知D选项不正确.故选:D.
【点睛】本题考查茎叶图的应用,考查众数、中位数、以及方差的大小比较,考查数据分析能力,属于基础题.
6.【答案】A
【分析】计算抽样比例,求出不到35岁的应抽取人数,再求50岁及以上的应抽取人数.
【详解】计算抽样比例为,所以不到35岁的应抽取(人,所以50岁及以上的应抽取(人.故选:.【版权所有:21教育】
7.【答案】D
【分析】列举法求得选物理和历史的所有种数,再利用古典概型求解
【详解】在2(物理,历史)选(化学、生物、地理、政治)选2中,选物理的有6种,分别为:
物化生、物化地、物化政、物生地、物生政、物地政,同时,选历史的也有6种,共计12种,
其中选择全理科的有1种,某考生选择全理科的概率是.故选:D
8.【答案】C
【分析】设出两人到达小王的时间,根据题意列出不等式组,利用几何概型计算公式进行求解即可.
【详解】设小王和外卖小哥到达小王所居住的楼下的时间分别为,以12:00点为开始算起,则有,在平面直角坐标系内,如图所示:图中阴影部分表示该不等式组的所表示的平面区域,21教育名师原创作品
所以小王在楼下等候外卖小哥的时间不超过5分钟的概率为:.
故选:C
【点睛】本题考查了几何概型中的面积型公式,考查了不等式组表示的平面区域,考查了数学运算能力.
9.【答案】D
【分析】根据回归直线方程可以判断与具有正线性相关关系,回归直线过样本的中心点,该中学某高中女生身高增加1cm,则其体重约增加0.85kg,该中学某高中女生身高为160cm,只能估计其体重,不能得出体重一定是多少.www-2-1-cnjy-com
【详解】根据回归直线方程,但看函数图象是单调递增,可以判断与具有正线性相关关系,所以A选项说法正确;回归直线过样本的中心点,所以B选项说法正确;
根据斜率得该中学某高中女生身高增加1cm,则其体重约增加0.85kg,所以C选项说法正确;
该中学某高中女生身高为160cm,根据回归直线方程只能估计其体重,D选项说“可断定其体重必为50.29kg”,这种说法错误.故选:D
【点睛】此题考查线性回归直线相关概念辨析,考查基础知识的掌握情况.
10. 【答案】D
【分析】根据直方图求出,求出的频率,可判断①;求出的频率,可判断②;根据中位数是从左到右频率为的分界点,先确定在哪个区间,再求出占该区间的比例,求出中位数,判断③.
【详解】由,,
的频率为,①正确;
的频率为,②正确;
的频率为,的频率为,中位数在且占该组的,
故中位数为,③正确.故选:D.
【点睛】本题考查补全直方图,由直方图求频率和平均数,属于基础题
11. 【答案】A
【分析】由二进制的转化为十进制的方法,只要一次累加个位数字上的数该数为的权重,即可得到转化,求得答案.
【详解】由题意知,,,根据十进制与八进制的转化可得,所以,故选A.
【点睛】本题主要考查了算法的概念及其应用,其中解答中熟记十进制与八进制的转化方法是解答的关键,着重考查了推理与运算能力,属于基础题.
12. 【答案】A
【分析】利用求出的范围,再利用几何概型即可求解.
【详解】方程有实根,则,即,解得,
所以方程有实根的概率为.故选:A
【点睛】本题考查了几何概型-长度型,考查了基本运算求解能力,属于基础题.
13.【答案】4
【分析】模拟程序运行,观察变量值,判断循环条件可得.
【详解】第一次循环:;第二次循环:,;第三次循环:;第四次循环:,退出循环,此时输出的值为4.故答案为:4
【点睛】本题考查程序框_??????è???????????_结构,模拟程序运行是解决问题的常用方法,如果循环次数较多,可以通过模拟程序运行确定程序功能,运用其他数学知识求解.
14.【答案】10565
【分析】先将6进制数化为十进制数,再用除取余法将十进制数化为8进制数即可得解.
【详解】,
又:,
,
,
,
把余数从下往上排序:10565.
即:.
故答案为:10565
【点睛】关键点点睛:考查进位制的转换,关键是熟练掌握除取余法及其进位制的数转化为十进制数的方法,属于中档题.
15.【答案】36
【分析】由频率分布直方图求出成绩不低于60分的频率,由此能求出成绩不低于60分的人数.
【详解】解:某班48名学生参加建国70周年知识竞赛,成绩都在区间,上,
由频率分布直方图知:成绩不低于60分的频率为:,
则成绩不低于60分的人数为.故答案为:36.
16.【答案】
【详解】由,得﹣2≤x≤0,由此利用几何概型概率计算公式能求出事件“”发生的概率.∵,∴﹣2≤x≤0,∵在区间[﹣3,5]上随机取一个实数x,∴由几何概型概率计算公式得:
事件“”发生的概率为p==.故答案为.
【点睛】本题考查了几何概型概率的_?±?????????¨?????¨_几何概型的概率公式来求其概率时,几何“测度”可以是长度、面积、体积、角度等,其中对于几何度量为长度,面积、体积时的等可能性主要体现在点落在区域Ω上任置都是等可能的,而对于角度而言,则是过角的顶点的一条射线落在Ω的区域(事实也是角)任一位置是等可能的.
17.答案见解析.
【分析】因为函数是分段函数,可设计一个选择语句,求出函数的任一函数值.
【详解】
算法如下:
输入;
若,则执行,若,则执行;
输出;
输出.
18.【解析】因为1147=888×1+259,
888=259×3+111,259=111×2+37,111=37×3,所以888与1 147的最大公约数是37.
【一题多解】此题也可以利用更相减损术来求:
1147-88_8=259???_888-259=629,629-259=370,370-259=111,259-111=148,148-111=37,
111-37=7474-37=37.
所以888与1147的最大公约数为37.
19. 【答案】(1);(2);(3)
【详解】
试题分析:(1)根据所有的基本事件的个数为,而所得点数相同的情况有种,从而求得事件“两颗骰子点数相同”的概率;(2)根据所有的基本事件的个数,求所求的“点数之和小于”的基本事件的个数,最后利用概率计算公式求解即可;(3)根据所有的基本事件的个数,求所求的“点数之和等于或大于”的基本事件的个数,最后利用概率计算公式求解即可.
试题解析:抛掷两颗骰子,总的事件有个.
(1)记“两颗骰子点数相同”为事件,则事件有6个基本事件,
∴
(2)记“点数之和小于7”为事件,则事件有15个基本事件,
∴
(3)记“点数之和等于或大于11”为事件,则事件有3个基本事件,
∴.
考点:古典概型.
20. 【答案】(Ⅰ);(Ⅱ)74.5;(Ⅲ)65分.
【分析】
(1)根据频率和为1,即小矩形面积和为1,求;(Ⅱ)利用每组数据中点值乘以本组的频率和,计算平均数;(Ⅲ)首先计算录取比例,根据录取比例求分数线.21cnjy.com
【详解】
(Ⅰ)由题意,
解得.
(Ⅱ)这些应聘者笔试成绩的平均数为.
(Ⅲ)根据题意,录取的比例为0.75,
设分数线定为,根据频率分布直方图可知,且,
解得.故估计应该把录取的分数线定为65分.
21.【答案】(1)0.3,直方图见解析;(2)121,;(3).
【分析】
(1)利用频率和为1求解;(2)利用小矩形中点乘以各组频率求和得平均数,利用左右面积平分求中位数;(3)利用古典概型结合间接法求解.21*cnjy*com
【详解】
(1)由频率分布直方图,得:
分数在,内的频率为:.
,补全后的直方图如图所示.
(2)由频率分布直方图得:
平均分为:
,的频率为,
,的频率为:,
中位数为:.
(3)用分层抽样的方法在分数段为,的学生中抽取一个容量为6的样本,
则分数段为,中抽取的学生数为:人,
分数段为,中抽取的学生数为:人,
将该样本看成一个总体,从中任取2个,基本事件总数,
至多有1人在分数段,内包含的基本事件为:,
至多有1人在分数段,内的概率(A).
22.【答案】(1)1800人;(2)7,0.24,8;(3).
【分析】
(1)根据高_????????§?????????_样比列出方程求解;(2)根据频率、频数与总数的关系计算;(3)列举出5名高二学生中任选2人的所有可能结果,再确定2人中恰好为一男一女的可能,利用古典概型概率公式进行求解.
【详解】
(1)设该校学生总数为n,
由题意,解得n=1800,
所以该校学生总数为1800人.
(2)由题意,?解得x=7,,
.
(3)记“选中的2人恰好为一男一女”为事件?A,
记5名高二学生中女生为F1,F2,男生为M1,M2,M3,
从中任选2人有以下情况:(F1,F2),(F1,M1),(F1,M2),(F1,M3),(F2,M1),(F2,M2),(F2,M3),www.21-cn-jy.com
(M1,M2),(M1,M3),(M2,M3),
基本事件共有10个,它们是等可能的,
事件A包含的基本事件有6个,故P(A)==,
所以选中的2人恰好为一男一女的概率为.
【点睛】本题考查分层抽样、频率分布表、古典概型的概率计算,属于基础题.
_21?????????è?????(www.21cnjy.com)_
2020-2021学年高一数学下学期期末复习自测(必修三)
(时间120分钟,满分150分)
选择题(每小题5分,共计60分)
1.半径为的圆的面积公式为,当时,则计算面积的流程图为( )
A.
B.
C.
D.
2.已知一组数据1,2,3,4,5,那么这组数据的方差为( )
A. B.2 C. D.3
3.某地区的高一新生中,来自_???é?¨????????°???_的学生有2400人,中部丘陵地区的学生有1600人,西部山区的学生有1000人.计划从中选取100人调查学生的视力情况,现已了解到来自东部、中部、西部三个地区学生的视力情况有较大差异,而这三个地区男女生视力情况差异不大,在下面的抽样方法中,最合理的抽样方法是( )2·1·c·n·j·y
A.简单随机抽样 B.按性别分层抽样
C.系统抽样 D.按地区分层抽样
4.用秦九韶算法求多项式f(x)=0.5x5+4x4-3x2+x-1当x=3的值时,先算的是( )
A.3×3=9 B.0.5×35=121.5
C.0.5×3+4=5.5 D.(0.5×3+4)×3=16.5
5.为了保障广大人民群众的身体健康,在新冠肺炎疫情防控期间,有关部门对辖区内家药店所销售的、两种型号的口罩进行了抽检,每家药店抽检包口罩(每包只),家药店中抽检的、型号口罩不合格数(Ⅰ、Ⅱ)的茎叶图如图所示,则下列描述不正确的是( )
A.估计型号口罩的合格率小于型号口罩的合格率
B.Ⅰ组数据的众数大于Ⅱ组数据的众数
C.Ⅰ组数据的中位数大于Ⅱ组数据的中位数
D.Ⅰ组数据的方差大于Ⅱ组数据的方差
6.某单位共有名职工,其中不到岁的有人,岁的有人,岁及以上的有人,现用分层抽样的方法,从中抽出名职工了解他们的健康情况.如果已知岁的职工抽取了人,则岁及以上的职工抽取的人数为( )【来源:21cnj*y.co*m】
A. B. C. D.
7.某省在新的高考改革方案中规定:每位考生的高考成绩是按照3(语文、数学、英语)(物理、历史)选(化学、生物、地理、政治)选2的模式设置的,则某考生选择全理科的概率是( )
A. B. C. D.
8.小王因上班繁忙,来不及做午_é?????????????????_外卖.假设小王和外卖小哥都在12:00~12:10之间随机到达小王所居住的楼下,则小王在楼下等候外卖小哥的时间不超过5分钟的概率是( )
A. B. C. D.
9.凤鸣山中学的高中女生体重 (单位:kg)与身高(单位:cm)具有线性相关关系,根据一组样本数据(),用最小二乘法近似得到回归直线方程为,则下列结论中不正确的是( )
A.与具有正线性相关关系
B.回归直线过样本的中心点
C.若该中学某高中女生身高增加1cm,则其体重约增加0.85kg
D.若该中学某高中女生身高为160cm,则可断定其体重必为50.29kg.
10.为了更好地支持“中小型企_?????????????±????_某市决定对部分企业的税收进行适当的减免,某机构调查了当地的中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,下面三个结论:
①样本数据落在区间的频率为0.45;
②如果规定年收入在500万元以内的企业才能享受减免税政策,估计有55%的当地中小型企业能享受到减免税政策;
③样本的中位数为480万元.
其中正确结论的个数为
A.0 B.1 C.2 D.3
11.自然界中具有两种稳定状态的组件普遍存在,如开关的开和关、电路的通和断等,非常适合表示计算机中的数,所以现在使用的计算机设计为二进制.二进制以为基数,只用和两个数表示数,逢进,二进制数与十进制数遵循一样的运算规则,它们可以相互转化,如.我国数学史上,清代汪莱的《参两算经》是较早系统论述非十进制数的文献,总结出了八进制乘法口决:,,,则八进制下等于
A. B. C. D.
12.方程有实根的概率为( )
A. B. C. D.
二、填空题(每小题5分,共计20分)
13.阅读如图所示的程序框图,运行相应的程序,则输出的值为__________.
14.请把6进制数化成8进制数: .
15.某班48名学生参加建国70周年知识竞赛,成绩都在区间,上,其频率分布直方图如图所示,则成绩不低于60分的人数为___________.21*cnjy*com
在区间[]上随机取一个实数,则事件“”发生的概率为____.
三、解答题(共计70分)
17.(7分)已知函数,设计一个算法,求函数的任一函数值.
18.(7分)用辗转相除法求888与1147的最大公约数.
19.(12分) 抛掷两颗骰子,计算:
(1)事件“两颗骰子点数相同”的概率;
(2)事件“点数之和小于7”的概率;
(3)事件“点数之和等于或大于11”的概率.
20.(14分)某企业招聘,一共有200名应聘者参加笔试他们的笔试成绩都在内,按照分组,得到如下频率分布直方图:21·世纪*教育网
(Ⅰ)求图中的值;
(Ⅱ)求全体应聘者笔试成绩的平均数;(每组数据以区间中点值为代表)
(Ⅲ)该企业根据笔试成绩从高到低进行录取,若计划录取150人,估计应该把录取的分数线定为多少.
21.(15分)某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段,,,,,,后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:21世纪教育网版权所有
(1)求分数在,内的频率,并补全这个频率分布直方图;
(2)估计本次考试的平均分及中位数;
(3)用分层抽样的方法在分数段为,的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段,内的概率.21教育网
22.(15分_?????°???è????????_情期间,为确保“停课不停学”,各校精心组织了线上教学活动.开学后,某校采用分层抽样的方法从三个年级的学生中抽取一个容量为150的样本进行关于线上教学实施情况的问卷调查.已知该校高一年级共有学生660人,抽取的样本中高二年级有50人,高三年级有45人.下表是根据抽样调查情况得到的高二学生日睡眠时间(单位:h)的频率分布表.
分组 频数 频率
5 0.10
8 0.16
x 0.14
12 y
10 0.20
z
合计 50 1
(1)求该校学生总数;
(2)求频率分布表中实数x,y,z的值;
(3)已知日睡眠时间在区间[_6???6.5)_的5名高二学生中,有2名女生,3名男生,若从中任选2人进行面谈,则选中的2人恰好为一男一女的概率.21·cn·jy·com
参考答案
1.【答案】B
【分析】因为处理输入和输出框是平行四边形,据此即可选出答案.
【详解】输入和输出框是平行四边形,故计算面积的流程图为B.故选:B.
2.【答案】B
【分析】先由平均数的计算公式计算出平均数,再根据方差的公式计算即可.
【详解】由题可得;
所以这组数据的方差 故选:B.
【点睛】本题考查方差的定义:一般地设个数据:的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动越大,方差越小,波动越小.2-1-c-n-j-y
3.【答案】D
【分析】根据抽样方法的特征,即可得出结论.
【详解】由于该地区东部、中部、西部三个地区学生的视力情况有较大差异,故按地区分层抽样.
【点睛】本题主要考查抽样方法,熟记每种抽样方法的特征即可,属于基础题型.
4.【答案】C
【详解】f(x)=((((_0.5x+4_)x+0)x-3)x+1)x-1,按递推方法,从里到外先算0.5x+4的值,将x=3代入求得0.5×3+4=5.5.故选C.【来源:21·世纪·教育·网】
5.【答案】D
【分析】根据茎叶图中的_??°???è??????????¤_种型号口罩的合格率,可判断A选项的正误;求出两组数据的众数,可判断B选项的正误;求出两组数据的中位数,可判断C选项的正误;利用排除法可判断D选项的正误.【出处:21教育名师】
【详解】对于A选项,由茎叶图可知,型号口罩的不合格数为,
型口罩的不合格数为,
型号口罩的合格率为,型口罩的合格率为,
所以,型口罩的合格率小于型口罩的合格率,A选项正确;
对于B选项,Ⅰ组数据的众数为,Ⅱ组数据的众数,B选项正确;
对于C选项,Ⅰ组数据的中位数为,Ⅱ组数据的,C选项正确;
由排除法可知D选项不正确.故选:D.
【点睛】本题考查茎叶图的应用,考查众数、中位数、以及方差的大小比较,考查数据分析能力,属于基础题.
6.【答案】A
【分析】计算抽样比例,求出不到35岁的应抽取人数,再求50岁及以上的应抽取人数.
【详解】计算抽样比例为,所以不到35岁的应抽取(人,所以50岁及以上的应抽取(人.故选:.【版权所有:21教育】
7.【答案】D
【分析】列举法求得选物理和历史的所有种数,再利用古典概型求解
【详解】在2(物理,历史)选(化学、生物、地理、政治)选2中,选物理的有6种,分别为:
物化生、物化地、物化政、物生地、物生政、物地政,同时,选历史的也有6种,共计12种,
其中选择全理科的有1种,某考生选择全理科的概率是.故选:D
8.【答案】C
【分析】设出两人到达小王的时间,根据题意列出不等式组,利用几何概型计算公式进行求解即可.
【详解】设小王和外卖小哥到达小王所居住的楼下的时间分别为,以12:00点为开始算起,则有,在平面直角坐标系内,如图所示:图中阴影部分表示该不等式组的所表示的平面区域,21教育名师原创作品
所以小王在楼下等候外卖小哥的时间不超过5分钟的概率为:.
故选:C
【点睛】本题考查了几何概型中的面积型公式,考查了不等式组表示的平面区域,考查了数学运算能力.
9.【答案】D
【分析】根据回归直线方程可以判断与具有正线性相关关系,回归直线过样本的中心点,该中学某高中女生身高增加1cm,则其体重约增加0.85kg,该中学某高中女生身高为160cm,只能估计其体重,不能得出体重一定是多少.www-2-1-cnjy-com
【详解】根据回归直线方程,但看函数图象是单调递增,可以判断与具有正线性相关关系,所以A选项说法正确;回归直线过样本的中心点,所以B选项说法正确;
根据斜率得该中学某高中女生身高增加1cm,则其体重约增加0.85kg,所以C选项说法正确;
该中学某高中女生身高为160cm,根据回归直线方程只能估计其体重,D选项说“可断定其体重必为50.29kg”,这种说法错误.故选:D
【点睛】此题考查线性回归直线相关概念辨析,考查基础知识的掌握情况.
10. 【答案】D
【分析】根据直方图求出,求出的频率,可判断①;求出的频率,可判断②;根据中位数是从左到右频率为的分界点,先确定在哪个区间,再求出占该区间的比例,求出中位数,判断③.
【详解】由,,
的频率为,①正确;
的频率为,②正确;
的频率为,的频率为,中位数在且占该组的,
故中位数为,③正确.故选:D.
【点睛】本题考查补全直方图,由直方图求频率和平均数,属于基础题
11. 【答案】A
【分析】由二进制的转化为十进制的方法,只要一次累加个位数字上的数该数为的权重,即可得到转化,求得答案.
【详解】由题意知,,,根据十进制与八进制的转化可得,所以,故选A.
【点睛】本题主要考查了算法的概念及其应用,其中解答中熟记十进制与八进制的转化方法是解答的关键,着重考查了推理与运算能力,属于基础题.
12. 【答案】A
【分析】利用求出的范围,再利用几何概型即可求解.
【详解】方程有实根,则,即,解得,
所以方程有实根的概率为.故选:A
【点睛】本题考查了几何概型-长度型,考查了基本运算求解能力,属于基础题.
13.【答案】4
【分析】模拟程序运行,观察变量值,判断循环条件可得.
【详解】第一次循环:;第二次循环:,;第三次循环:;第四次循环:,退出循环,此时输出的值为4.故答案为:4
【点睛】本题考查程序框_??????è???????????_结构,模拟程序运行是解决问题的常用方法,如果循环次数较多,可以通过模拟程序运行确定程序功能,运用其他数学知识求解.
14.【答案】10565
【分析】先将6进制数化为十进制数,再用除取余法将十进制数化为8进制数即可得解.
【详解】,
又:,
,
,
,
把余数从下往上排序:10565.
即:.
故答案为:10565
【点睛】关键点点睛:考查进位制的转换,关键是熟练掌握除取余法及其进位制的数转化为十进制数的方法,属于中档题.
15.【答案】36
【分析】由频率分布直方图求出成绩不低于60分的频率,由此能求出成绩不低于60分的人数.
【详解】解:某班48名学生参加建国70周年知识竞赛,成绩都在区间,上,
由频率分布直方图知:成绩不低于60分的频率为:,
则成绩不低于60分的人数为.故答案为:36.
16.【答案】
【详解】由,得﹣2≤x≤0,由此利用几何概型概率计算公式能求出事件“”发生的概率.∵,∴﹣2≤x≤0,∵在区间[﹣3,5]上随机取一个实数x,∴由几何概型概率计算公式得:
事件“”发生的概率为p==.故答案为.
【点睛】本题考查了几何概型概率的_?±?????????¨?????¨_几何概型的概率公式来求其概率时,几何“测度”可以是长度、面积、体积、角度等,其中对于几何度量为长度,面积、体积时的等可能性主要体现在点落在区域Ω上任置都是等可能的,而对于角度而言,则是过角的顶点的一条射线落在Ω的区域(事实也是角)任一位置是等可能的.
17.答案见解析.
【分析】因为函数是分段函数,可设计一个选择语句,求出函数的任一函数值.
【详解】
算法如下:
输入;
若,则执行,若,则执行;
输出;
输出.
18.【解析】因为1147=888×1+259,
888=259×3+111,259=111×2+37,111=37×3,所以888与1 147的最大公约数是37.
【一题多解】此题也可以利用更相减损术来求:
1147-88_8=259???_888-259=629,629-259=370,370-259=111,259-111=148,148-111=37,
111-37=7474-37=37.
所以888与1147的最大公约数为37.
19. 【答案】(1);(2);(3)
【详解】
试题分析:(1)根据所有的基本事件的个数为,而所得点数相同的情况有种,从而求得事件“两颗骰子点数相同”的概率;(2)根据所有的基本事件的个数,求所求的“点数之和小于”的基本事件的个数,最后利用概率计算公式求解即可;(3)根据所有的基本事件的个数,求所求的“点数之和等于或大于”的基本事件的个数,最后利用概率计算公式求解即可.
试题解析:抛掷两颗骰子,总的事件有个.
(1)记“两颗骰子点数相同”为事件,则事件有6个基本事件,
∴
(2)记“点数之和小于7”为事件,则事件有15个基本事件,
∴
(3)记“点数之和等于或大于11”为事件,则事件有3个基本事件,
∴.
考点:古典概型.
20. 【答案】(Ⅰ);(Ⅱ)74.5;(Ⅲ)65分.
【分析】
(1)根据频率和为1,即小矩形面积和为1,求;(Ⅱ)利用每组数据中点值乘以本组的频率和,计算平均数;(Ⅲ)首先计算录取比例,根据录取比例求分数线.21cnjy.com
【详解】
(Ⅰ)由题意,
解得.
(Ⅱ)这些应聘者笔试成绩的平均数为.
(Ⅲ)根据题意,录取的比例为0.75,
设分数线定为,根据频率分布直方图可知,且,
解得.故估计应该把录取的分数线定为65分.
21.【答案】(1)0.3,直方图见解析;(2)121,;(3).
【分析】
(1)利用频率和为1求解;(2)利用小矩形中点乘以各组频率求和得平均数,利用左右面积平分求中位数;(3)利用古典概型结合间接法求解.21*cnjy*com
【详解】
(1)由频率分布直方图,得:
分数在,内的频率为:.
,补全后的直方图如图所示.
(2)由频率分布直方图得:
平均分为:
,的频率为,
,的频率为:,
中位数为:.
(3)用分层抽样的方法在分数段为,的学生中抽取一个容量为6的样本,
则分数段为,中抽取的学生数为:人,
分数段为,中抽取的学生数为:人,
将该样本看成一个总体,从中任取2个,基本事件总数,
至多有1人在分数段,内包含的基本事件为:,
至多有1人在分数段,内的概率(A).
22.【答案】(1)1800人;(2)7,0.24,8;(3).
【分析】
(1)根据高_????????§?????????_样比列出方程求解;(2)根据频率、频数与总数的关系计算;(3)列举出5名高二学生中任选2人的所有可能结果,再确定2人中恰好为一男一女的可能,利用古典概型概率公式进行求解.
【详解】
(1)设该校学生总数为n,
由题意,解得n=1800,
所以该校学生总数为1800人.
(2)由题意,?解得x=7,,
.
(3)记“选中的2人恰好为一男一女”为事件?A,
记5名高二学生中女生为F1,F2,男生为M1,M2,M3,
从中任选2人有以下情况:(F1,F2),(F1,M1),(F1,M2),(F1,M3),(F2,M1),(F2,M2),(F2,M3),www.21-cn-jy.com
(M1,M2),(M1,M3),(M2,M3),
基本事件共有10个,它们是等可能的,
事件A包含的基本事件有6个,故P(A)==,
所以选中的2人恰好为一男一女的概率为.
【点睛】本题考查分层抽样、频率分布表、古典概型的概率计算,属于基础题.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
