人教A必修4综合测试-2020-2021学年高一数学下学期期末专项复习(人教A版必修4)(含解析)
文档属性
| 名称 | 人教A必修4综合测试-2020-2021学年高一数学下学期期末专项复习(人教A版必修4)(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-22 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2020-2021学年高一数学下学期期末复习自测(必修四)
(时间120分钟,满分150分)
选择题(每小题5分,共计60分)
1.( ).
A. B. C. D.
2.函数的定义域是( )
A. B.
C. D.
3.函数的单调递增区间为( )
A. B.
C. D.
4.如果函数y=3cos(2x+φ)的图象关于点(,0)中心对称,那么|φ|的最小值为( )
A. B. C. D.
5.已知,且,则( )
A.1 B.3 C. D.5
6.已知向量,,若,则实数的值为( )
A. B. C. D.
7.已知,与的夹角为,则在上的投影为( )
A.2 B.1 C. D.
8.在中,,是上一点,若,则实数的值为( ).
A. B. C. D.
9.已知,则的值为( )
A. B. C. D.
10. ( )
A. B. C. D.
11.函数在区间上的值域为( )
A. B. C. D.
12.不等式的解集为
A. B. C. D.
二、填空题(每小题5分,共计20分)
13.将函数的图像向左平移个单位后所得函数图像关于原点中心对称,则_________.
14.化简为_____
15.在直角坐标系中,为原点,O、A、B不共线,,则________
16.若(tanα-1)(tanβ-1)=2,则α+β=_____.
三、解答题(共计70分)
17.(8分)已知,向量,.
(1)若向量与平行,求k的值;
(2)若向量与的夹角为钝角,求k的取值范围.
18.(10分)已知,,,.
(1)求的值;
(2)求的值.
19.(10分)已知A、B、C是的三内角,且,是判断此三角形的形状.
20.(12分)若函数,的图象经过点,且相邻的两个零点差的绝对值为6.
(1)求函数的解析式;
(2)若将函数的图象向右平移3个单位后得到函数的图象,当时,求的值域.
21.(15分)如图为一个_???è???¤??????????_该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面距离是h.
(1)求h与θ间的函数关系式;
(2)设从OA开始转动,经过t秒后到达OB,求h与t之间的函数关系式,并求缆车到达最高点时用的最少时间是多少?21教育网
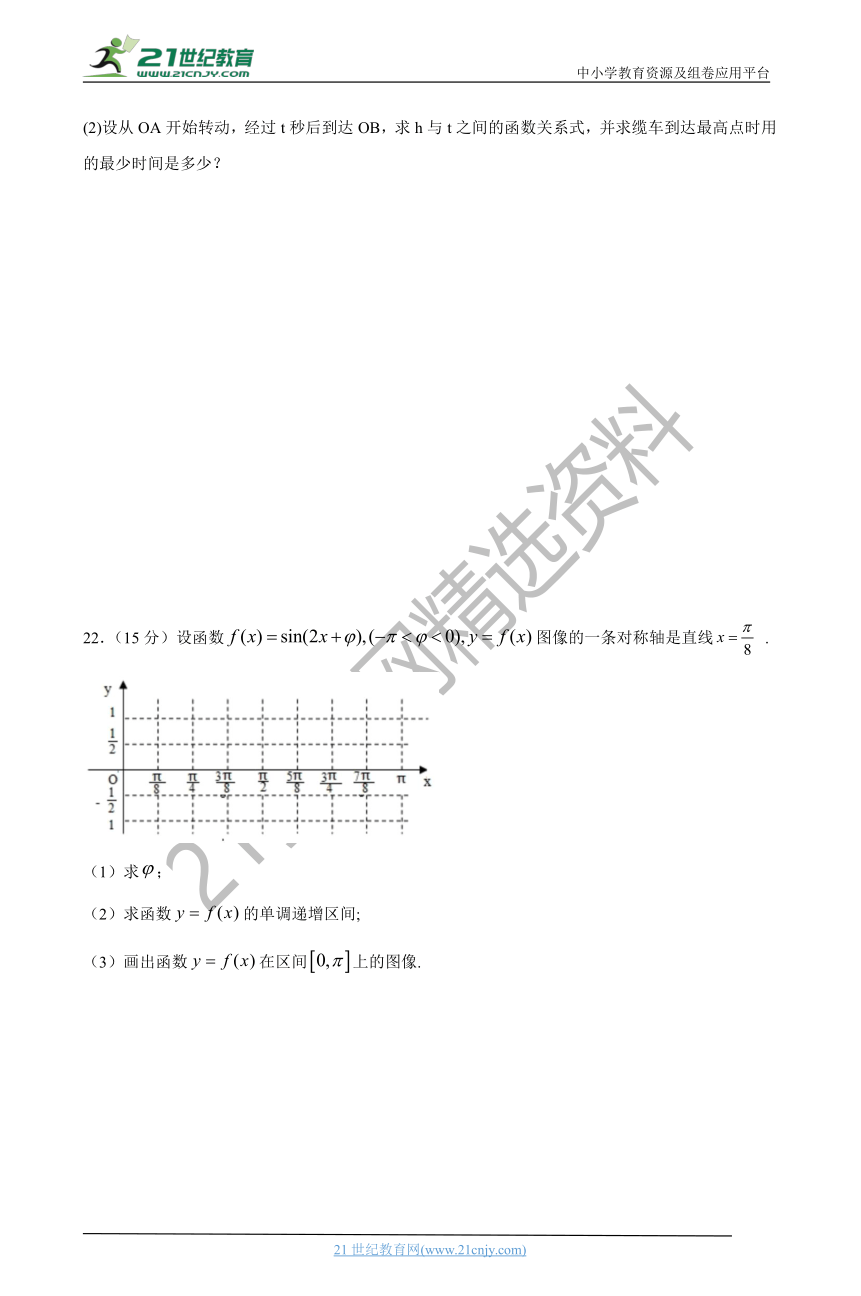
22.(15分)设函数图像的一条对称轴是直线 .
(1)求;
(2)求函数的单调递增区间;
(3)画出函数在区间上的图像.
参考答案
1.【答案】C
【分析】直接利用诱导公式计算可得;
【详解】.故选:C
【点睛】本题考查正弦函数求值,诱导公式的应用,属于基础题.
2.【答案】D
【分析】利用负数不能开偶次方根,再由三角不等式的解法求解.
【详解】由,得,
解得.
所以函数的定义域是.故选:D.
3.【答案】A
【分析】根据题意得到,,再解不等式即可得到答案.
【详解】当,时,函数单调递增,
即当,时,函数单调递增.故选:A
【点睛】本题主要考查正弦型函数的单调区间,属于简单题.
4.【答案】A
【分析】先根据函数y=3cos(2x+φ)的图象关于点中心对称,令x代入函数使其等于0,求出φ的值,进而可得|φ|的最小值.21cnjy.com
【详解】∵函数y=3cos(2x+φ)的图象关于点中心对称.
∴∴
当时,有.故选:A.
【点睛】本题主要考查三角函数的简单性质,考查学生对这些知识的理解掌握水平和分析推理计算能力,属基础题.www.21-cn-jy.com
5.【答案】D
【分析】利用向量的垂直,求出,然后求解向量的模.
【详解】,,且,可得,解得,
所以,则.故选:.
6.【答案】A
【分析】由题意,求得,,根据,列出方程,即可求解.
【详解】由题意,向量,,
可得,,
因为,所以,解得.故选:A.
7.【答案】A
【分析】向量在上的正射影的数量为|,又,从而根据条件分别求()?和即可.
【详解】∵,与的夹角为,∴,
由此可得,∴.
设与的夹角为,∵()?,∴,
可得向量在上的正射影的数量为|.故选A.
【点睛】(1)本题主要考查向量的投影和向量的数量积计算,意在考查学生对这些知识的掌握水平和分析推理计算能力.(2) 在上的“投影”的概念:叫做向量在上的“投影”, 向量在向量上的投影,它表示向量在向量上的投影对应的有向线段的数量.它是一个实数,可以是正数,可以是负数,也可以是零.【来源:21·世纪·教育·网】
8.【答案】D
【分析】根据向量共线转化为,利用三点共线求实数的取值.
【详解】,又因为,所以,即,
所以,
因为点三点共线,所以,解得:.故选:D
【点睛】本题考查向量共线,平面向量基本定理,重点考查转化思想,计算能力,属于基础题型.
9.【答案】D
【分析】利用两角和与差的正弦公式,诱导公式化简已知等式可得,进而利用诱导公式,二倍角公式化简所求即可求解.21·cn·jy·com
【详解】
因为
,
所以,故选:D
10.【答案】C
【分析】利用两角和的正切公式,特殊角的三角函数值化简已知即可求解.
【详解】
.故选:.
11.【答案】B
【分析】先将函数转化为,再根据,利用余弦函数的性质求解.
【详解】函数
因为,所以,
,所以函数的值域为,故选:B
12.【答案】B
【分析】将不等式化为,然后根据的范围得到的范围,结合正弦函数的图象解不等式即可.
【详解】∵,∴.
∵,∴,∴,
∴.∴原不等式的解集为.故选B.
【点睛】解答本题的关键是将原不等式化为的形式,然后将作为一个整体,并结合正弦函数的图象求解,其中整体代换和数形结合是解决类似问题的常用思路.
13.【答案】
【分析】先根据函数平移变换得平移后的解析式为,再根据其图象关于原点中心对称得,进而计算得.
【详解】根据题意得函数的图像向左平移个单位后得到的函数解析式为:,
由函数图象关于原点中心对称,故,即
所以.故答案为:
【点睛】三角函数的图象变换,提倡“先平移,后伸缩”,但“先伸缩,后平移”也常出现在题目中,所以也必须熟练掌握.无论是哪种变形,切记每一个变换总是对字母而言. 2·1·c·n·j·y
函数是奇函数 ;
函数是偶函数;
函数是奇函数;
函数是偶函数.
14.【答案】1
【分析】根据同角三角函数的基本关系式对所求表达式进行化简,由此求得表达式的值.
【详解】
依题意.
【点睛】本小题主要考查同角三角函数的基本关系式,考查化归与转化的数学思想方法,属于基础题.
15.【答案】0
【分析】
根据向量的线性运算求出,根据对应关系求出的值即可.
【详解】,,,
,,.故答案为:0.
16.【答案】kπ-,k∈Z
【解析】
【分析】由已知化简可得tanα+tanβ=tanαtanβ-1代入两角和的正切公式,可以求出的正切值,在求得的值.www-2-1-cnjy-com
【详解】
(tanα-1)(tanβ-1)=2?tanαtanβ-tanα-tanβ+1=2?tanα+tanβ=tanαtanβ-1
?=-1.
即tan(α+β)=-1,∴α+β=kπ-,k∈Z.故答案为:
【点睛】本题目考查了正切函数的和差角公式,属于基础题.
17.【答案】(1)或;(2).
【分析】
(1)利用向量平行的坐标表示列式计算即得结果;
(2)利用,且不共线,列式计算即得结果.
【详解】
(1)依题意,,,
又,得,即
解得或;
(2)与的夹角为钝角,则,即,
即,解得或.
由(1)知,当时,与平行,舍去,
所以.
【点睛】思路点睛:两向量夹角为锐角(或钝角)的等价条件:
(1)两向量夹角为锐角,等价于,且不共线;
(2)两向量夹角为钝角,等价于,且不共线.
18.【答案】(1);(2).
【分析】
(1)由已知利用同角三角函数基本关系式可求,的值,进而根据,利用两角差的余弦函数公式即可求解.21·世纪*教育网
(2)利用二倍角公式可求,的值,进而即可代入求解.
【详解】
(1)因为,
所以
又因为,
所以
所以
(2)因为,
所以
所以
【点睛】本题主要考查了同角三角函数基本关系式,两角差的余弦函数公式,二倍角公式在三角函数化简求值中的应用,考查了计算能力和转化思想.2-1-c-n-j-y
19.【答案】见解析.
【分析】根据并结合进行化简,最后得到,于是得,进而得到三角形的形状.
【详解】由题意可得,∴,
,
又,
,
,
,
又B、C是三角形内角,
∴,
,
∴三角形为等腰三角形.
【点睛】判断三角形形状的常用方法
(1)“角化边”:利用正弦、余弦定理把已知条件转化为只含边的关系,通过因式分解、配方等得出边的相应关系,从而得到三角形的形状.21*cnjy*com
(2)“边化角”:利用正弦、余_?????????????·????_条件转化为只含内角的三角函数间的关系,通过三角函数恒等变形,得出内角的关系,从而得到三角形的形状,此时要注意应用A+B+C=π这个结论.
20.【答案】(1);(2).
【分析】
(1)求出函数的周期,求解,利用函数经过的点,求解,然后得到函数的解析;
(2)利用函数的图象的平移变换推出函数的解析式,求解相位的范围,然后求解函数的最值,即可得的值域.【来源:21cnj*y.co*m】
【详解】
(1)因为相邻的两个零点差的绝对值为6,
记的周期为,则,
所以,所以,
所以;
因为的图象经过点,所以,
所以,又,所以 ,
所以函数的解析式为.
(2)由(1)知,
因为将函数的图象向右平移3个单位后得到函数的图象,
所以函数的解析式为,
当时,,所以,
综上,当时,的值域为.
【点睛】
关键点点睛:由函数的部分图象确定解析式关键在于确定参数,的值.
(1)一般可由图象上的最大值、最小值来确定.
(2)因为,所以往往通过求周期来确定,可通过已知曲线与轴的交点从而确定,即相邻的最高点与最低点之间的距离为;相邻的两个最高点(或最低点)之间的距离为;相邻的两个零点之间的距离为.【出处:21教育名师】
21.【答案】(1) ;(2) ,缆车到达最高点时,用的时间最少为30 s.
【分析】
(1)建立平面直角坐标系,结合条件求出点的坐标后可得h与θ间的函数关系式.(2)由t s转过的弧度数为可得θ与t的关系,代入(1)中的关系式可得h与t之间的函数解析式,然后通过最值可得所求的最小时间.【版权所有:21教育】
【详解】
(1)以圆心原点,建立如图所示的坐标系,如下图所示,
则以为始边,为终边的角为,
故点B坐标为.
∴.
(2)点A在圆上转动的角速度是,故t s转过的弧度数为,
∴,
∴.
令,
得,
∴,
∴.
令,得t=30 s.
∴缆车到达最高点时,用的时间最少为30 s.
【点睛】用三角函_??°?¨????è§???????_际问题主要有两种:一种是用已知的模型去分析解决实际问题,另一种是需要建立精确的或者数据拟合的模型去解决问题,尤其是利用数据建立拟合函数解决实际问题,体现了新课标中“数学建模”的本质.21世纪教育网版权所有
22. 【答案】(1);(2);(3)答案见解析.
【分析】
(1)由正弦函数的对数轴求出;
(2)根据正弦函数性质求得增区间;
(3)列表描点连线可得图象.注意五点法中的特殊点和区间的端点.
【详解】
(1)是函数的一条对称轴,
,即
,
(2)由(1)知
由题意得
所以函数的单调递增区间为
(3)由可知
故函数在区间上的图像为:
【点睛】本题考查三角函数的对称性,单调性,考查用列表描点法作正弦型函数的图象.属于基础题.
_21?????????è?????(www.21cnjy.com)_
2020-2021学年高一数学下学期期末复习自测(必修四)
(时间120分钟,满分150分)
选择题(每小题5分,共计60分)
1.( ).
A. B. C. D.
2.函数的定义域是( )
A. B.
C. D.
3.函数的单调递增区间为( )
A. B.
C. D.
4.如果函数y=3cos(2x+φ)的图象关于点(,0)中心对称,那么|φ|的最小值为( )
A. B. C. D.
5.已知,且,则( )
A.1 B.3 C. D.5
6.已知向量,,若,则实数的值为( )
A. B. C. D.
7.已知,与的夹角为,则在上的投影为( )
A.2 B.1 C. D.
8.在中,,是上一点,若,则实数的值为( ).
A. B. C. D.
9.已知,则的值为( )
A. B. C. D.
10. ( )
A. B. C. D.
11.函数在区间上的值域为( )
A. B. C. D.
12.不等式的解集为
A. B. C. D.
二、填空题(每小题5分,共计20分)
13.将函数的图像向左平移个单位后所得函数图像关于原点中心对称,则_________.
14.化简为_____
15.在直角坐标系中,为原点,O、A、B不共线,,则________
16.若(tanα-1)(tanβ-1)=2,则α+β=_____.
三、解答题(共计70分)
17.(8分)已知,向量,.
(1)若向量与平行,求k的值;
(2)若向量与的夹角为钝角,求k的取值范围.
18.(10分)已知,,,.
(1)求的值;
(2)求的值.
19.(10分)已知A、B、C是的三内角,且,是判断此三角形的形状.
20.(12分)若函数,的图象经过点,且相邻的两个零点差的绝对值为6.
(1)求函数的解析式;
(2)若将函数的图象向右平移3个单位后得到函数的图象,当时,求的值域.
21.(15分)如图为一个_???è???¤??????????_该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面距离是h.
(1)求h与θ间的函数关系式;
(2)设从OA开始转动,经过t秒后到达OB,求h与t之间的函数关系式,并求缆车到达最高点时用的最少时间是多少?21教育网
22.(15分)设函数图像的一条对称轴是直线 .
(1)求;
(2)求函数的单调递增区间;
(3)画出函数在区间上的图像.
参考答案
1.【答案】C
【分析】直接利用诱导公式计算可得;
【详解】.故选:C
【点睛】本题考查正弦函数求值,诱导公式的应用,属于基础题.
2.【答案】D
【分析】利用负数不能开偶次方根,再由三角不等式的解法求解.
【详解】由,得,
解得.
所以函数的定义域是.故选:D.
3.【答案】A
【分析】根据题意得到,,再解不等式即可得到答案.
【详解】当,时,函数单调递增,
即当,时,函数单调递增.故选:A
【点睛】本题主要考查正弦型函数的单调区间,属于简单题.
4.【答案】A
【分析】先根据函数y=3cos(2x+φ)的图象关于点中心对称,令x代入函数使其等于0,求出φ的值,进而可得|φ|的最小值.21cnjy.com
【详解】∵函数y=3cos(2x+φ)的图象关于点中心对称.
∴∴
当时,有.故选:A.
【点睛】本题主要考查三角函数的简单性质,考查学生对这些知识的理解掌握水平和分析推理计算能力,属基础题.www.21-cn-jy.com
5.【答案】D
【分析】利用向量的垂直,求出,然后求解向量的模.
【详解】,,且,可得,解得,
所以,则.故选:.
6.【答案】A
【分析】由题意,求得,,根据,列出方程,即可求解.
【详解】由题意,向量,,
可得,,
因为,所以,解得.故选:A.
7.【答案】A
【分析】向量在上的正射影的数量为|,又,从而根据条件分别求()?和即可.
【详解】∵,与的夹角为,∴,
由此可得,∴.
设与的夹角为,∵()?,∴,
可得向量在上的正射影的数量为|.故选A.
【点睛】(1)本题主要考查向量的投影和向量的数量积计算,意在考查学生对这些知识的掌握水平和分析推理计算能力.(2) 在上的“投影”的概念:叫做向量在上的“投影”, 向量在向量上的投影,它表示向量在向量上的投影对应的有向线段的数量.它是一个实数,可以是正数,可以是负数,也可以是零.【来源:21·世纪·教育·网】
8.【答案】D
【分析】根据向量共线转化为,利用三点共线求实数的取值.
【详解】,又因为,所以,即,
所以,
因为点三点共线,所以,解得:.故选:D
【点睛】本题考查向量共线,平面向量基本定理,重点考查转化思想,计算能力,属于基础题型.
9.【答案】D
【分析】利用两角和与差的正弦公式,诱导公式化简已知等式可得,进而利用诱导公式,二倍角公式化简所求即可求解.21·cn·jy·com
【详解】
因为
,
所以,故选:D
10.【答案】C
【分析】利用两角和的正切公式,特殊角的三角函数值化简已知即可求解.
【详解】
.故选:.
11.【答案】B
【分析】先将函数转化为,再根据,利用余弦函数的性质求解.
【详解】函数
因为,所以,
,所以函数的值域为,故选:B
12.【答案】B
【分析】将不等式化为,然后根据的范围得到的范围,结合正弦函数的图象解不等式即可.
【详解】∵,∴.
∵,∴,∴,
∴.∴原不等式的解集为.故选B.
【点睛】解答本题的关键是将原不等式化为的形式,然后将作为一个整体,并结合正弦函数的图象求解,其中整体代换和数形结合是解决类似问题的常用思路.
13.【答案】
【分析】先根据函数平移变换得平移后的解析式为,再根据其图象关于原点中心对称得,进而计算得.
【详解】根据题意得函数的图像向左平移个单位后得到的函数解析式为:,
由函数图象关于原点中心对称,故,即
所以.故答案为:
【点睛】三角函数的图象变换,提倡“先平移,后伸缩”,但“先伸缩,后平移”也常出现在题目中,所以也必须熟练掌握.无论是哪种变形,切记每一个变换总是对字母而言. 2·1·c·n·j·y
函数是奇函数 ;
函数是偶函数;
函数是奇函数;
函数是偶函数.
14.【答案】1
【分析】根据同角三角函数的基本关系式对所求表达式进行化简,由此求得表达式的值.
【详解】
依题意.
【点睛】本小题主要考查同角三角函数的基本关系式,考查化归与转化的数学思想方法,属于基础题.
15.【答案】0
【分析】
根据向量的线性运算求出,根据对应关系求出的值即可.
【详解】,,,
,,.故答案为:0.
16.【答案】kπ-,k∈Z
【解析】
【分析】由已知化简可得tanα+tanβ=tanαtanβ-1代入两角和的正切公式,可以求出的正切值,在求得的值.www-2-1-cnjy-com
【详解】
(tanα-1)(tanβ-1)=2?tanαtanβ-tanα-tanβ+1=2?tanα+tanβ=tanαtanβ-1
?=-1.
即tan(α+β)=-1,∴α+β=kπ-,k∈Z.故答案为:
【点睛】本题目考查了正切函数的和差角公式,属于基础题.
17.【答案】(1)或;(2).
【分析】
(1)利用向量平行的坐标表示列式计算即得结果;
(2)利用,且不共线,列式计算即得结果.
【详解】
(1)依题意,,,
又,得,即
解得或;
(2)与的夹角为钝角,则,即,
即,解得或.
由(1)知,当时,与平行,舍去,
所以.
【点睛】思路点睛:两向量夹角为锐角(或钝角)的等价条件:
(1)两向量夹角为锐角,等价于,且不共线;
(2)两向量夹角为钝角,等价于,且不共线.
18.【答案】(1);(2).
【分析】
(1)由已知利用同角三角函数基本关系式可求,的值,进而根据,利用两角差的余弦函数公式即可求解.21·世纪*教育网
(2)利用二倍角公式可求,的值,进而即可代入求解.
【详解】
(1)因为,
所以
又因为,
所以
所以
(2)因为,
所以
所以
【点睛】本题主要考查了同角三角函数基本关系式,两角差的余弦函数公式,二倍角公式在三角函数化简求值中的应用,考查了计算能力和转化思想.2-1-c-n-j-y
19.【答案】见解析.
【分析】根据并结合进行化简,最后得到,于是得,进而得到三角形的形状.
【详解】由题意可得,∴,
,
又,
,
,
,
又B、C是三角形内角,
∴,
,
∴三角形为等腰三角形.
【点睛】判断三角形形状的常用方法
(1)“角化边”:利用正弦、余弦定理把已知条件转化为只含边的关系,通过因式分解、配方等得出边的相应关系,从而得到三角形的形状.21*cnjy*com
(2)“边化角”:利用正弦、余_?????????????·????_条件转化为只含内角的三角函数间的关系,通过三角函数恒等变形,得出内角的关系,从而得到三角形的形状,此时要注意应用A+B+C=π这个结论.
20.【答案】(1);(2).
【分析】
(1)求出函数的周期,求解,利用函数经过的点,求解,然后得到函数的解析;
(2)利用函数的图象的平移变换推出函数的解析式,求解相位的范围,然后求解函数的最值,即可得的值域.【来源:21cnj*y.co*m】
【详解】
(1)因为相邻的两个零点差的绝对值为6,
记的周期为,则,
所以,所以,
所以;
因为的图象经过点,所以,
所以,又,所以 ,
所以函数的解析式为.
(2)由(1)知,
因为将函数的图象向右平移3个单位后得到函数的图象,
所以函数的解析式为,
当时,,所以,
综上,当时,的值域为.
【点睛】
关键点点睛:由函数的部分图象确定解析式关键在于确定参数,的值.
(1)一般可由图象上的最大值、最小值来确定.
(2)因为,所以往往通过求周期来确定,可通过已知曲线与轴的交点从而确定,即相邻的最高点与最低点之间的距离为;相邻的两个最高点(或最低点)之间的距离为;相邻的两个零点之间的距离为.【出处:21教育名师】
21.【答案】(1) ;(2) ,缆车到达最高点时,用的时间最少为30 s.
【分析】
(1)建立平面直角坐标系,结合条件求出点的坐标后可得h与θ间的函数关系式.(2)由t s转过的弧度数为可得θ与t的关系,代入(1)中的关系式可得h与t之间的函数解析式,然后通过最值可得所求的最小时间.【版权所有:21教育】
【详解】
(1)以圆心原点,建立如图所示的坐标系,如下图所示,
则以为始边,为终边的角为,
故点B坐标为.
∴.
(2)点A在圆上转动的角速度是,故t s转过的弧度数为,
∴,
∴.
令,
得,
∴,
∴.
令,得t=30 s.
∴缆车到达最高点时,用的时间最少为30 s.
【点睛】用三角函_??°?¨????è§???????_际问题主要有两种:一种是用已知的模型去分析解决实际问题,另一种是需要建立精确的或者数据拟合的模型去解决问题,尤其是利用数据建立拟合函数解决实际问题,体现了新课标中“数学建模”的本质.21世纪教育网版权所有
22. 【答案】(1);(2);(3)答案见解析.
【分析】
(1)由正弦函数的对数轴求出;
(2)根据正弦函数性质求得增区间;
(3)列表描点连线可得图象.注意五点法中的特殊点和区间的端点.
【详解】
(1)是函数的一条对称轴,
,即
,
(2)由(1)知
由题意得
所以函数的单调递增区间为
(3)由可知
故函数在区间上的图像为:
【点睛】本题考查三角函数的对称性,单调性,考查用列表描点法作正弦型函数的图象.属于基础题.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
