六年级数学上册课件 1.7 长方体和正方体的表面积 苏教版(23张PPT)
文档属性
| 名称 | 六年级数学上册课件 1.7 长方体和正方体的表面积 苏教版(23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-22 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
长方体和正方体
第9课时
长方体和正方体的底面积
1.经历长方体和正方体的统一体积计算公式的推导过程,进一步认识两种几何体的基本特征及它们之间的关系。?
2.会应用长方体、正方体体积的统一计算公式解决一些简单的实际问题。?
3.知道我国古代数学家在两千多年前就掌握了长方体体积的计算方法,增强学生的民族自豪感和勇超先贤的信心和决心。
学习目标
长方体的长、宽、高分别是a、b、h,它的体积V
是多少?
正方体的棱长是a,它的体积V
是多少?
复习导入
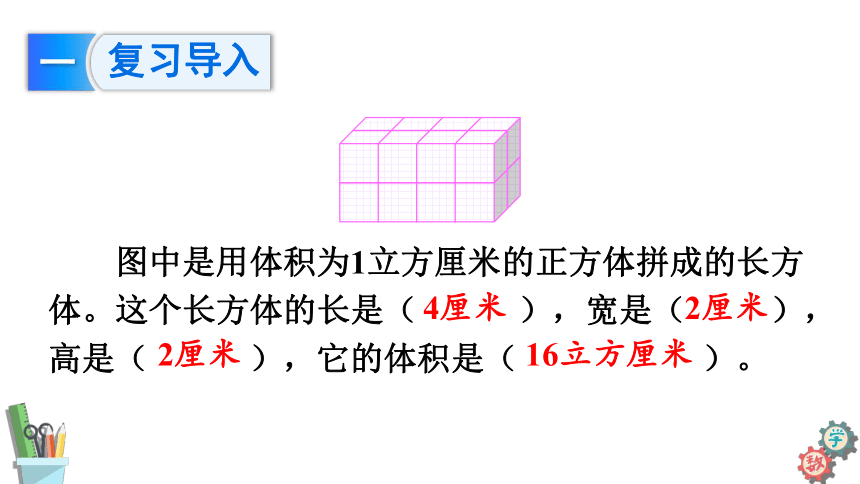
图中是用体积为1立方厘米的正方体拼成的长方体。这个长方体的长是(
),宽是(
),高是(
),它的体积是(
)。
4厘米
2厘米
2厘米
16立方厘米
“方自乘,以高乘之即积尺。”
——刘徽(汉)
这句话的意思是:有两个面是正方形的长方体体积的计算方法,先用边长×边长得底面积,再乘高就得到长方体的体积。
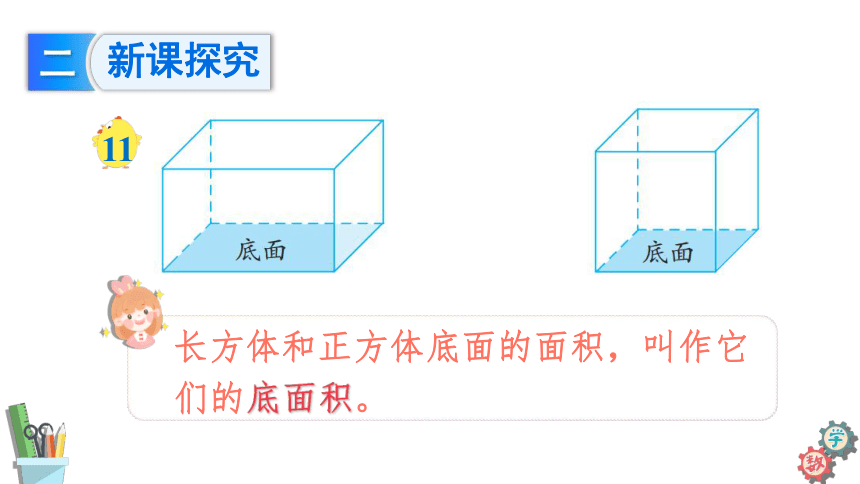
11
长方体和正方体底面的面积,叫作它们的底面积。
怎样计算长方体和正方体的底面积?
a
b
h
a
a
a
长方体的底面积=长×宽
S=ab
长方体的底面积=棱长×棱长
S=a?
?
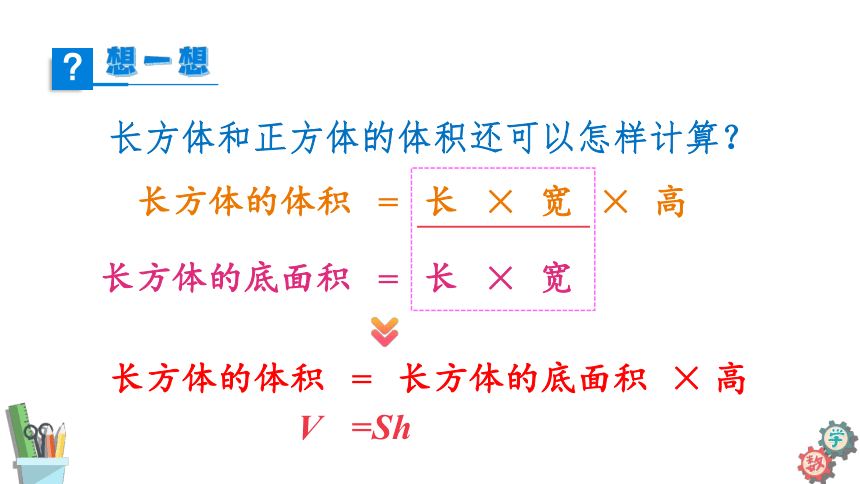
长方体和正方体的体积还可以怎样计算?
长方体的体积
长
宽
×
=
×
高
长方体的底面积
长
宽
×
=
长方体的体积
长方体的底面积
=
×
高
V
=Sh
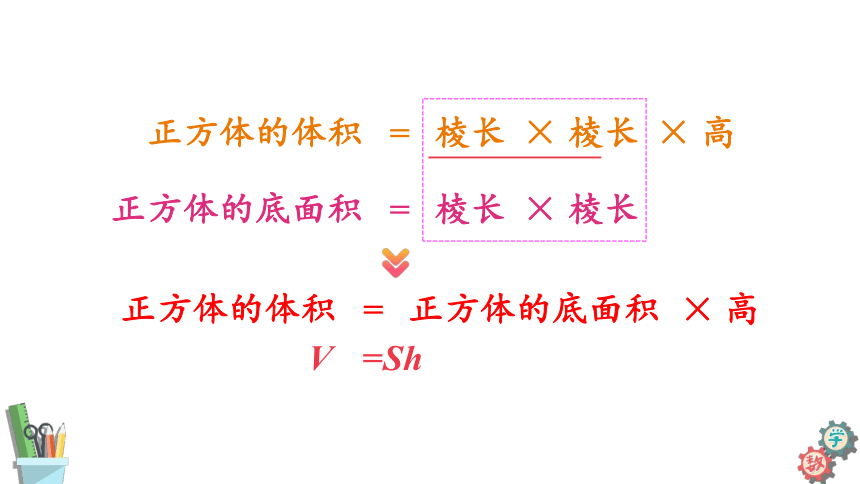
正方体的体积
棱长
棱长
×
=
×
高
正方体的底面积
棱长
棱长
×
=
正方体的体积
正方体的底面积
=
×
高
V
=Sh
长方体(或正方体)的体积
底面积
=
如果用V表示长方体(或正方体)的体积,用S、h分别表示长方(或正方形)的底面积、高,上面的公式可以写成:V=Sh。
V
=
S
×
高
h
1.
先计算长方体和正方体的地面积,再计算它们
的体积。
S=20×16=320(m2)
V=320×10=3200(m3)
S=5×5=25(m2)
V=25×5=125(m3)
2.
一个长方体的底面积是15平方厘米,高6厘
米。求它的体积。
V=15×6=90(cm3)
答:它的体积是90立方厘米。
3.选一选
1.一个长方体长、宽、高都扩大3倍,体积(
)。
A.
扩大为原来的6倍。
B.扩大为原来的3倍
C.扩大到原来的27倍。
2.一个长方体的体积是24m?,长是6m,宽是2m,高是(
)。
A.
4
B.
2
C.6
C
B
4.判断
1.一个长方体木箱横放、竖放占的空间不一样大。
(
)
2.体积相等的正方体,表面积也相等。
(
)
3.正方体的体积比长方体的体积大。
(
)
4.一个正方体橡皮泥被捏成一个长方体后,虽然形状变了,但它所占的空间的大小没变。
(
)
×
√
×
√
5.
一根长方体木料,长3米,横截面是一个边长
0.3米的正方形。这根木料的横截面面积是多
少平方米?体积是多少立方米?
S=0.3×0.3=0.09(m2)
V=0.09×3=0.27(m3)
答:这根木料的横截面面积是0.09平方米,体
积是0.27平方米。
4.光明小学修筑一条长60米、宽12米的直跑道。先铺上
0.3米厚的三合土。再铺上0.03米厚的塑胶。需要三合
土、塑胶各多少立方米?
60×12×0.3=216(立方米)
答:需要三合土216立方米,塑胶21.6立方米。
60×12×0.03=21.6(立方米)
7.一个底面是正方形的长方体,所有棱长的和是100厘米,它的高是7厘米,这个长方体的体积是多少立方厘米?
上下两个面的8条棱长相等。
4条高的长度相等,是7厘米。
由棱长的和是100求出底面正方形的边长。
7.一个底面是正方形的长方体,所有棱长的和是100厘米,它的高是7厘米,这个长方体的体积是多少立方厘米?
(100-7×4)÷8
=72÷8
=9(厘米)
9×9×7=567(立方厘米)
答:这个长方体的体积是567立方厘米。
1.把一块棱长是8厘米的正方体橡皮泥捏成一个底面积是32平方厘米的长方体,这个长方体的高是多少厘米?
8×8×8÷32=16(cm)
答:这个长方体的高是16厘米。
2.一个长方体,如果高增加2厘米,就变成一个正方体。
这时表面积比原来增加了56平方厘米。原来长方体的
体积是多少立方厘米?
7×7×(7-2)=245(平方厘米)
答:原来长方体的体积是245立方厘米。
14÷2=7(厘米)
56÷4=14(平方厘米)
3.一根长方体木料沿横截面切成2段,表面积增加了80平方厘米。
已知木料长3米,它的体积是多少立方分米?
3米
底面积:0.8÷2=0.4(平方分米)
体积:0.4×30=12(立方分米)
答:它的体积是12立方分米。
3米=30分米
80平方厘米=0.8平方分米
长方体和正方体体积的统一公式:
长方体和正方体底面的面积,叫作它们的底面积。
长方体或正方体的体积=底面积×高,用字母表示为:V=Sh。
长方体和正方体
第9课时
长方体和正方体的底面积
1.经历长方体和正方体的统一体积计算公式的推导过程,进一步认识两种几何体的基本特征及它们之间的关系。?
2.会应用长方体、正方体体积的统一计算公式解决一些简单的实际问题。?
3.知道我国古代数学家在两千多年前就掌握了长方体体积的计算方法,增强学生的民族自豪感和勇超先贤的信心和决心。
学习目标
长方体的长、宽、高分别是a、b、h,它的体积V
是多少?
正方体的棱长是a,它的体积V
是多少?
复习导入
图中是用体积为1立方厘米的正方体拼成的长方体。这个长方体的长是(
),宽是(
),高是(
),它的体积是(
)。
4厘米
2厘米
2厘米
16立方厘米
“方自乘,以高乘之即积尺。”
——刘徽(汉)
这句话的意思是:有两个面是正方形的长方体体积的计算方法,先用边长×边长得底面积,再乘高就得到长方体的体积。
11
长方体和正方体底面的面积,叫作它们的底面积。
怎样计算长方体和正方体的底面积?
a
b
h
a
a
a
长方体的底面积=长×宽
S=ab
长方体的底面积=棱长×棱长
S=a?
?
长方体和正方体的体积还可以怎样计算?
长方体的体积
长
宽
×
=
×
高
长方体的底面积
长
宽
×
=
长方体的体积
长方体的底面积
=
×
高
V
=Sh
正方体的体积
棱长
棱长
×
=
×
高
正方体的底面积
棱长
棱长
×
=
正方体的体积
正方体的底面积
=
×
高
V
=Sh
长方体(或正方体)的体积
底面积
=
如果用V表示长方体(或正方体)的体积,用S、h分别表示长方(或正方形)的底面积、高,上面的公式可以写成:V=Sh。
V
=
S
×
高
h
1.
先计算长方体和正方体的地面积,再计算它们
的体积。
S=20×16=320(m2)
V=320×10=3200(m3)
S=5×5=25(m2)
V=25×5=125(m3)
2.
一个长方体的底面积是15平方厘米,高6厘
米。求它的体积。
V=15×6=90(cm3)
答:它的体积是90立方厘米。
3.选一选
1.一个长方体长、宽、高都扩大3倍,体积(
)。
A.
扩大为原来的6倍。
B.扩大为原来的3倍
C.扩大到原来的27倍。
2.一个长方体的体积是24m?,长是6m,宽是2m,高是(
)。
A.
4
B.
2
C.6
C
B
4.判断
1.一个长方体木箱横放、竖放占的空间不一样大。
(
)
2.体积相等的正方体,表面积也相等。
(
)
3.正方体的体积比长方体的体积大。
(
)
4.一个正方体橡皮泥被捏成一个长方体后,虽然形状变了,但它所占的空间的大小没变。
(
)
×
√
×
√
5.
一根长方体木料,长3米,横截面是一个边长
0.3米的正方形。这根木料的横截面面积是多
少平方米?体积是多少立方米?
S=0.3×0.3=0.09(m2)
V=0.09×3=0.27(m3)
答:这根木料的横截面面积是0.09平方米,体
积是0.27平方米。
4.光明小学修筑一条长60米、宽12米的直跑道。先铺上
0.3米厚的三合土。再铺上0.03米厚的塑胶。需要三合
土、塑胶各多少立方米?
60×12×0.3=216(立方米)
答:需要三合土216立方米,塑胶21.6立方米。
60×12×0.03=21.6(立方米)
7.一个底面是正方形的长方体,所有棱长的和是100厘米,它的高是7厘米,这个长方体的体积是多少立方厘米?
上下两个面的8条棱长相等。
4条高的长度相等,是7厘米。
由棱长的和是100求出底面正方形的边长。
7.一个底面是正方形的长方体,所有棱长的和是100厘米,它的高是7厘米,这个长方体的体积是多少立方厘米?
(100-7×4)÷8
=72÷8
=9(厘米)
9×9×7=567(立方厘米)
答:这个长方体的体积是567立方厘米。
1.把一块棱长是8厘米的正方体橡皮泥捏成一个底面积是32平方厘米的长方体,这个长方体的高是多少厘米?
8×8×8÷32=16(cm)
答:这个长方体的高是16厘米。
2.一个长方体,如果高增加2厘米,就变成一个正方体。
这时表面积比原来增加了56平方厘米。原来长方体的
体积是多少立方厘米?
7×7×(7-2)=245(平方厘米)
答:原来长方体的体积是245立方厘米。
14÷2=7(厘米)
56÷4=14(平方厘米)
3.一根长方体木料沿横截面切成2段,表面积增加了80平方厘米。
已知木料长3米,它的体积是多少立方分米?
3米
底面积:0.8÷2=0.4(平方分米)
体积:0.4×30=12(立方分米)
答:它的体积是12立方分米。
3米=30分米
80平方厘米=0.8平方分米
长方体和正方体体积的统一公式:
长方体和正方体底面的面积,叫作它们的底面积。
长方体或正方体的体积=底面积×高,用字母表示为:V=Sh。
