2020-2021学年度上海市普陀区七年级下学期数学期末模拟试题(word版含解析)
文档属性
| 名称 | 2020-2021学年度上海市普陀区七年级下学期数学期末模拟试题(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 620.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-23 20:39:35 | ||
图片预览


文档简介
本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
2020-2021学年度上海市普陀区七年级下学期数学期末模拟卷
考试范围:12.1~15.2;考试时间:90分钟;
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题(共12分)
1.(本题2分)在实数,0,0.131131113…,中,属于无理数的是(
)
A.
B.0
C.0.131131113…
D.
2.(本题2分)要使式子有意义,则的取值范围是(
)
A.且
B.
C.
D.
3.(本题2分)如图,下列条件不能判断的是(
)
A.
B.
C.
D.
4.(本题2分)用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是(
)
A.SAS
B.AAS
C.ASA
D.SSS
5.(本题2分)若点
在轴上,则点在(
)
A.第一象限
B.第二象限
C.第三项县
D.第四象限
6.(本题2分)如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,
=15,DE=3,AB=6,则AC长是(
)
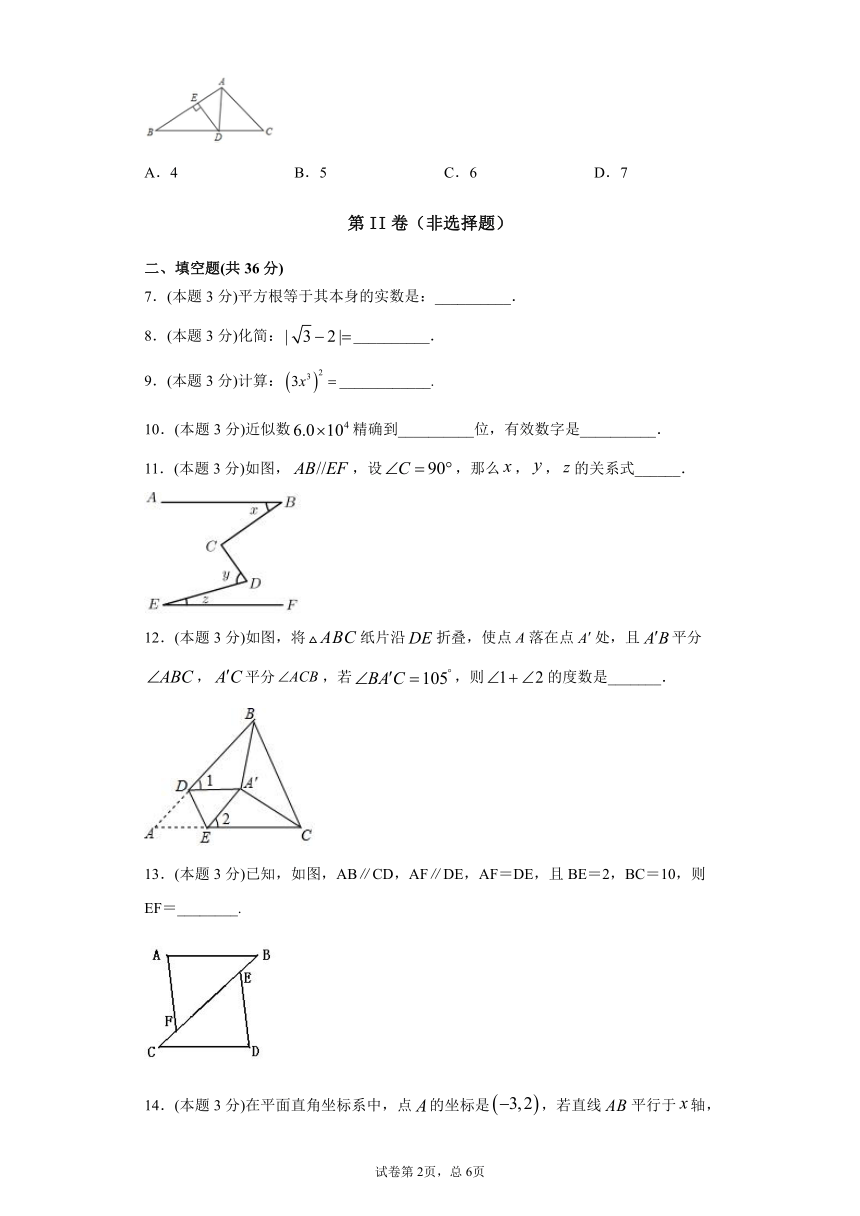
A.4
B.5
C.6
D.7
第II卷(非选择题)
二、填空题(共36分)
7.(本题3分)平方根等于其本身的实数是:__________.
8.(本题3分)化简:__________.
9.(本题3分)计算:____________.
10.(本题3分)近似数精确到__________位,有效数字是__________.
11.(本题3分)如图,,设,那么,,的关系式______.
12.(本题3分)如图,将纸片沿折叠,使点A落在点处,且平分,平分,若,则的度数是_______.
13.(本题3分)已知,如图,AB∥CD,AF∥DE,AF=DE,且BE=2,BC=10,则EF=________.
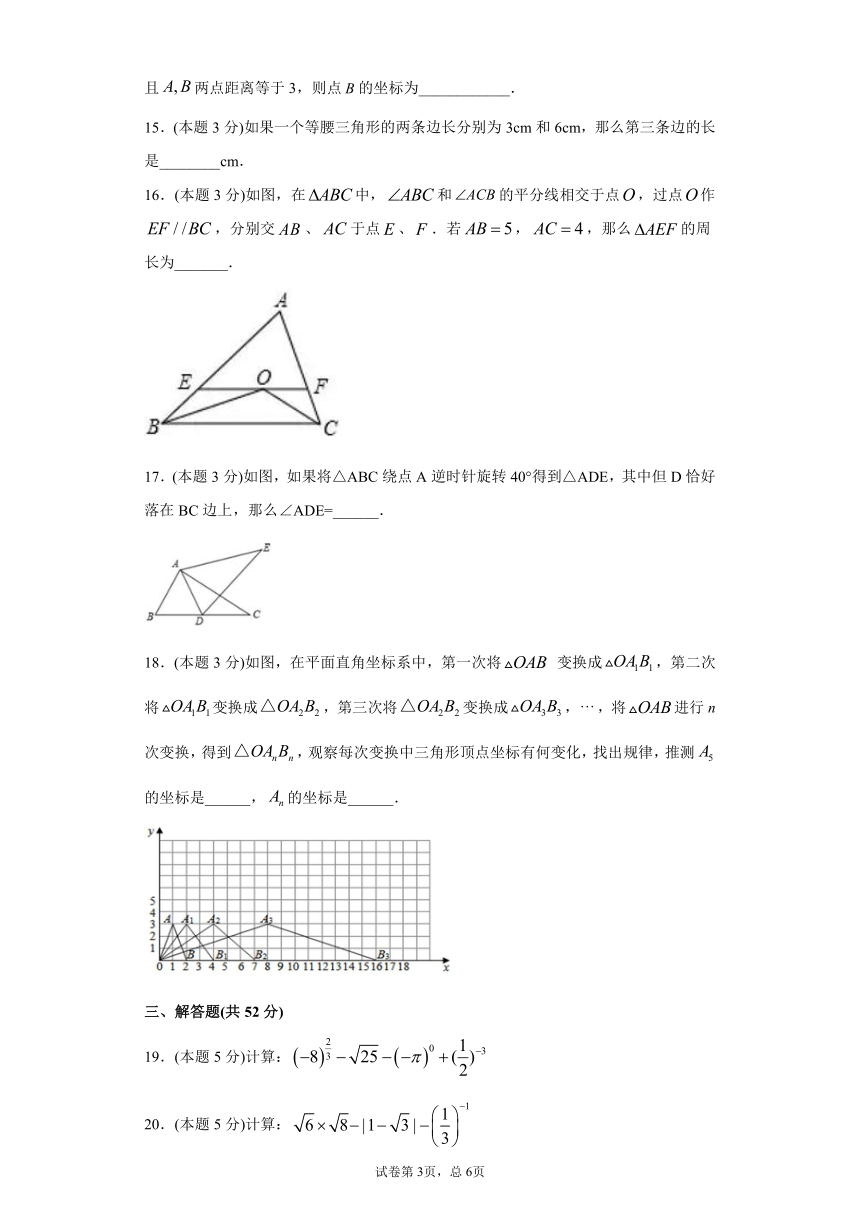
14.(本题3分)在平面直角坐标系中,点的坐标是,若直线平行于轴,且两点距离等于3,则点的坐标为____________.
15.(本题3分)如果一个等腰三角形的两条边长分别为3cm和6cm,那么第三条边的长是________cm.
16.(本题3分)如图,在中,和的平分线相交于点,过点作,分别交、于点、.若,,那么的周长为_______.
17.(本题3分)如图,如果将△ABC绕点A逆时针旋转40°得到△ADE,其中但D恰好落在BC边上,那么∠ADE=______.
18.(本题3分)如图,在平面直角坐标系中,第一次将
变换成,第二次将变换成,第三次将变换成,,将进行n次变换,得到,观察每次变换中三角形顶点坐标有何变化,找出规律,推测的坐标是______,的坐标是______.
三、解答题(共52分)
19.(本题5分)计算:
20.(本题5分)计算:
21.(本题5分)如图,已知直线AB、CD被直线EF所截,GE平分,GF平分,,ABCD吗?为什么?
答:
.
解:因为GE平分,GF平分(已知)
所以=2
.
=2
.(
)
所以+=
(等式性质)
因为(已知)
所以+=
.
所以ABCD(
).
22.(本题5分)如图,在△ABC
中,点
D、E
分别在
BC、AC
上且
BD=CE,AD=DE,
∠C
=∠ADE,
则∠B
=∠C,试填写说理过程.
解因为∠EDB
=∠C+∠DEC(
)
即∠ADB+∠ADE
=∠C+∠DEC
因为∠C
=∠ADE(
)
所以∠
=∠
(等式性质)
在△ABD
与△DCE
中,
所以△ABD
≌
△DCE(
)
所以∠B
=∠C(
)
23.(本题5分)如图,已知△ABC,请按下列要求作图:
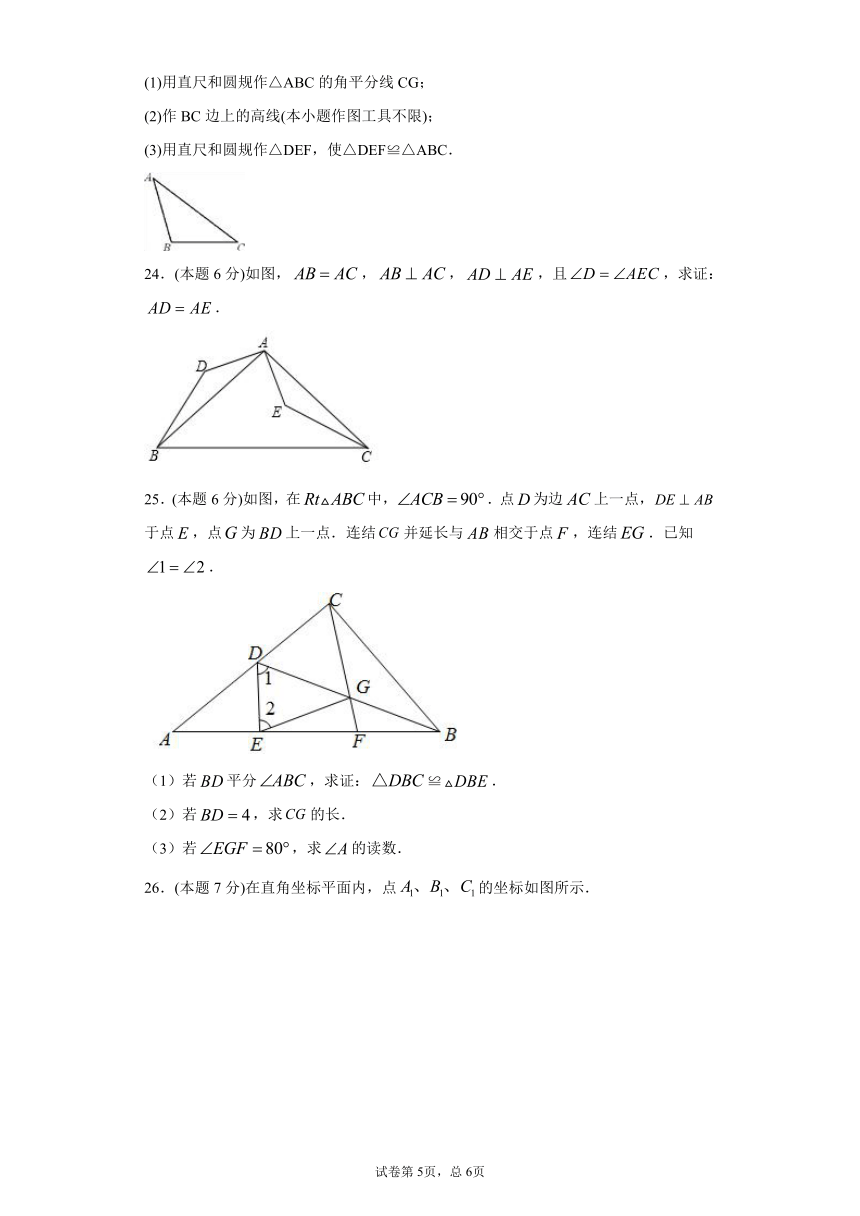
(1)用直尺和圆规作△ABC的角平分线CG;
(2)作BC边上的高线(本小题作图工具不限);
(3)用直尺和圆规作△DEF,使△DEF≌△ABC.
24.(本题6分)如图,,,,且,求证:.
25.(本题6分)如图,在中,.点为边上一点,于点,点为上一点.连结并延长与相交于点,连结.已知.
(1)若平分,求证:≌.
(2)若,求的长.
(3)若,求的读数.
26.(本题7分)在直角坐标平面内,点的坐标如图所示.
(1)请写出点的坐标.
点的坐标是
;
点的坐标是
;
点的坐标是
;
(2)点点绕原点逆时针旋转得到点,则点的坐标是
;
(3)若点与点关于原点对称,则点的坐标是
;
(4)将沿x周翻折得到点,则点的坐标是
;
(5)分别联结,得到,则的面积是
.
27.(本题8分)如图,在直角坐标平面内有两点、,且、两点之间的距离等于(为大于0的已知数),在不计算的数值条件下,完成下列两题:
(1)以学过的知识用一句话说出的理由;
(2)在轴上是否存在点,使是等腰三角形,如果存在,请写出点的坐标,并求的面积;如果不存在,请说明理由.
试卷第2页,总2页
试卷第1页,总1页
参考答案
1.C
【分析】
无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【详解】
解:是分数,属于有理数;
0,均为整数,属于有理数;
0.131131113…是无限不循环小数,属于无理数;
故选:C
【点睛】
此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.
2.A
【分析】
根据使分式和二次根式有意义的条件即可解答.
【详解】
根据题意可知:
,
∴.
故选:A.
【点睛】
本题考查使分式和二次根式有意义的条件.掌握分母不能为0和被开方数大于等于0是解答本题的关键.
3.C
【分析】
根据平行线的判定进行判断求解.
【详解】
解:A.
,根据同旁内角互补,两直线平行,可判定,故此选项不符合题意;
B.
,根据内错角相等,两直线平行可判定,故此选项不符合题意;
C.
,根据内错角相等,两直线平行可判定,但不能判断,故此选项符合题意;
D.
,根据同位角相等,两直线平行可判定,故此选项不符合题意;
故选:C.
【点睛】
本题考查平行线的判定,掌握平行线的判定方法正确推理论证是解题关键.
4.D
【分析】
根据三角形全等的判定与性质即可得出答案.
【详解】
解:根据作法可知:OC=O′C′,OD=O′D′,DC=D′C′
∴△OCD≌△O′C′D′(SSS)
∴∠COD=∠C′O′D′
∴∠AOB=∠A′O′B′
故选D.
【点睛】
本题考查的是三角形全等,属于基础题型,需要熟练掌握三角形全等的判定与性质.
5.B
【分析】
根据x轴上点的坐标的特点y=0,计算出a的值,从而得出点Q坐标,并判断点Q所在的象限
【详解】
解:∵点P(a,a-1)在x轴上,
∴a-1=0,
∴a=1
∴a-2=-1,a+1=2
则点Q的坐标为(-1,2),
∴点Q在第二象限
故选:B
【点睛】
本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
6.A
【分析】
根据角平分线上的点到角的两边的距离相等可得AC边上的高,再利用S△ABD+S△ACD=S△ABC,即可得解.
【详解】
解:作DF⊥AC于F,如图:
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF=3,
∵S△ABD+S△ACD=S△ABC,
∴,
∴AC=4.
故选:A.
【点睛】
本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.
7.0
【分析】
根据平方的特性从三个特殊数0,±1中找,即可得到答案.
【详解】
解:∵02=0,
∴平方根等于本身的是0;
故答案是:0
【点睛】
本题考查了平方根的定义,这类问题要记准三个特殊的数:0,±1.
8.
【分析】
先判断两个实数的大小关系,再根据绝对值的代数意义化简,进而得出答案.
【详解】
解:∵,
∴原式
,
故答案为:.
【点睛】
此题主要考查了绝对值的代数意义,正确判断实数的大小是解题关键.
9.
【分析】
根据积的乘方公式和幂的乘方公式计算即可
【详解】
;故答案为.
【点睛】
本题考查了积的乘方公式和幂的乘方公式,解题的关键是理解积的乘方公式和幂的乘方公式.
10.千;
6,0
【分析】
根据近似数的精确度和有效数字的定义求解.
【详解】
近似数=60000,精确到千位,有2个有效数字,有效数字是6和0.
故答案为:千;6和0.
【点睛】
本题考查了近似数和有效数字,理解近似数和有效数字是解题的关键.
11.
【分析】
过作,过作,根据平行线的性质可知,然后根据平行线的性质即可求解;
【详解】
如图,过作,过作,
∴,
∴,,,
∵,
∴,
∴,
∴,
∴,
∴.
故答案为:.
【点睛】
本题考查了平行线的性质,两直线平行同位角相等,两直线平行内错角相等,正确理解平行线的性质是解题的关键;
12.60°
【分析】
连接AA′.首先求出∠BAC,再证明∠1+∠2=2∠BAC即可解决问题.
【详解】
解:连接AA′.
∵A'B平分∠ABC,A'C平分∠ACB,∠BA'C=105°,
∴∠A′BC+∠A′CB=75°,
∴∠ABC+∠ACB=150°,
∴∠BAC=180°-150°=30°,
∵∠1=∠DAA′+∠DA′A,∠2=∠EAA′+∠EA′A,
由折叠可知:∠DAA′=∠DA′A,∠EAA′=∠EA′A,
∴∠1+∠2=2(∠DAA′+∠EAA′)=2∠BAC=60°,
故答案为:60°.
【点睛】
本题考查三角形的内角和定理、角平分线的定义、三角形的外角的性质等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识,属于中考常考题型.
13.6
【分析】
首先证明△ABF≌△DCE,根据全等三角形的性质可得BF=CE,再根据等式的性质可得CF=EB=2,进而可得EF的长.
【详解】
∵AB∥CD,AF∥DE,
∴∠B=∠C,∠AFB=∠DEC,
在△ABF和△CDE中
,
∴△ABF≌△DCE(AAS),
∴BF=CE,
∴BF?EF=CE?EF,
即CF=EB=2,
∵BC=10,
∴EF=10?2?2=6,
故答案为6.
【点睛】
此题考查全等三角形的判定与性质,解题关键在于得到CF=EB=2.
14.或
【分析】
根据平行于轴的直线上的点纵坐标相等,得出点B的纵坐标为2,再根据两点距离等于3,用A点的横坐标加3或减3即可
【详解】
∵点的坐标是,直线平行于轴,
∴B点的纵坐标为2;
∵两点距离等于3,
∴B点的横坐标为-3+3=0或-3-3=-6
∴B或
故答案为:或
【点睛】
本题涉及到的知识点为:平行于y轴的直线上的点的横坐标相等;一条直线上到一个定点为定长的点有2个.
15.6
【分析】
分“3cm为腰长”和“6cm为腰长”两种情况计算,再根据三边关系判断即可.
【详解】
解:分两种情况考虑:
若3cm为等腰三角形的腰长,则三边分别为3cm,3cm,6cm,因为3+3=6,不符合三边关系,故舍去;
若6cm为等腰三角形的腰长,则三边分别为6cm,6cm,3cm,符合三边关系,则第三条边的长是6cm.
故答案为:6.
【点睛】
本题考查了等腰三角形的性质及三边关系,掌握基础知识是关键,做题时注意分情况考虑.
16.
【分析】
根据角平分线的性质,可得∠EBO与∠OBC的关系,∠FCO与∠OCB的关系,根据平行线的性质,可得∠DOB与∠BOC的关系,∠FOC与∠OCB的关系,根据等腰三角形的判定,可得OE与BE的关系,OE与CE的关系,根据三角形的周长公式,可得答案.
【详解】
∵∠ABC与∠ACB的平分线相交于点O,
∴∠EBO=∠OBC,∠FCO=∠OCB.
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠EOB=∠EBO,∠FOC=∠FCO,
∴EO=BE,OF=FC.
C△AEF=AE+EF+AF=AE+BE+AF+CF=AB+AC=9.
故答案为:9.
【点睛】
本题考查了等腰三角形的判定与性质,利用等腰三角形的判定与性质是解题关键,又利用了角平分线的性质,平行线的性质.
17.70°
【分析】
由将△ABC绕点A逆时针旋转40°得到△ADE,可得AB=AD,∠BAD=40°,继而求得∠B的度数,然后由旋转的性质,可求得∠ADE的度数.
【详解】
解:∵将△ABC绕点A逆时针旋转40°得到△ADE,
∴AB=AD,∠BAD=40°,
∴∠B=∠ADB=70°,
∴∠ADE=∠B=70°.
故答案为:70°.
【点睛】
此题考查了旋转的性质以及等腰三角形的性质.注意掌握旋转前后图形的对应关系是关键.
18.
【分析】
根据图形写出点A系列的坐标,根据具体数值找到规律即可.
【详解】
解:,
的横坐标为,纵坐标都为3,
,即
故答案为:;.
【点睛】
本题考查点坐标的规律,涉及乘方知识,是重要考点,难度较易,掌握相关知识是解题关键.
19.6
【分析】
直接利用二次根式的性质以及分数值数幂的性质、零指数幂的性质、负指数幂的性质分别化简得出答案.
【详解】
解:原式
=
=6.
【点睛】
本题主要考查了实数运算,正确化简各数是解题关键.
20.
【分析】
根据二次根式的乘法,绝对值的性质、负整指数幂的运算法则解题.
【详解】
解:原式=
=
=
.
【点睛】
本题考查实数的混合运算,是重要考点
,难度较易,掌握相关知识是解题关键.
21.见解析
【分析】
根据角平分线的定义和平行线的判定方法推理可得结论.
【详解】
解:平行,理由如下:
因为GE平分∠AEF,GF平分∠EFC(已知),
所以∠AEF=2∠1,
∠EFC=2∠2,(角平分线的定义)
所以∠AEF+∠EFC=2(∠1+∠2)(等式性质),
因为∠1+∠2=90°(已知),
所以∠AEF+∠EFC=180°,
所以AB∥CD(同旁内角互补,两直线平行).
【点睛】
本题考查了平行线的判定,牢记平行线的三个判定定理是解决此类题目的关键.
22.见详解
【分析】
利用三角形的外角等于不相邻的两个内角的和可证∠ADB=∠DEC.根据“SAS”
证得△ABD≌△DCE即可.
【详解】
解:∵∠EDB
=∠C+∠DEC(三角形的外角性质)
即∠ADB+∠ADE
=∠C+∠DEC
∵∠C
=∠ADE(已知)
∴∠ADB
=∠DEC(等式性质)
在△ABD
与△DCE
中,
∴△ABD
≌
△DCE(SAS)
∴∠B
=∠C(全等三角形的对应角相等)
【点睛】
此题考查了三角形的外角性质和全等三角形的性质和判定,解决本题的关键是熟练掌握相关知识.
23.见解析
【分析】
(1)利用基本作图(作已知角的平分线)画∠ACB的平分线OG;
(2)过点A作AH⊥BC于H,则AH为BC边上的高;
(3)先作线段EF=BC,然后分别以E、F为圆心,BA和CA为半径画弧,两弧交于点D,则△DEF与△ABC全等.
【详解】
解:(1)如图1,CG为所作;
(2)如图1,AH为所作;
(3)如图2,△DEF为所作.
【点睛】
本题考查了作图﹣复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
24.见解析
【分析】
先求出∠CAE=∠BAD再利用AAS证明△ABD≌△ACE,即可解答.
【详解】
证明:∵AB⊥AC,AD⊥AE,
∴∠BAE+∠CAE=90°,∠BAE+∠BAD=90°,
∴∠CAE=∠BAD,
又AB=AC,,
∴△ABD≌△ACE(AAS),
∴.
【点睛】
此题考查全等三角形的判定与性质,解题关键在于判定三角形全等.
25.(1)见解析;(2)2;(3)40°
【分析】
(1)利用角平分线的定义及AAS定理证明三角形全等;
(2)根据等腰三角形的判定和性质求解;
(3)解法一:结合等边对等角,角平分线的定义及三角形内角和定理计算求解;
解法二:利用圆周角定理求解.
【详解】
解:(1)证明:∵,
∴,
∵,
∴.
∵平分,
∴.
又∵,
∴≌(AAS).
(2)∵在中,,
∴,.
∵,
∴,
∴.
∴在中,.
(3)解法一:∵,
∴.
∵,
∴
.
∴.
解法二:∵,
∴点,,,在以点为圆心的圆上,
∴,
∴.
【点睛】
本题考查全等三角形的判定和性质,等腰三角形的判定和性质,也考查圆周角定理,掌握相关性质定理正确推理计算是解题关键.
26.(1);;;(2);(3);(4);(5)
【分析】
(1)根据在坐标系所处的位置即可得到点的坐标;
(2)根据旋转的性质即可求得点的坐标;
(3)根据中心对称的性质即可求得点的坐标;
(4)根据轴对称的性质即可求得点的坐标;
(5)的面积由正方形的面积减去两个三角形的面积求得即可.
【详解】
解:(1)在直角坐标平面内,点、、的坐标如图所示:
点的坐标是;点的坐标是;点的坐标是,
故答案为;;.
(2)将点绕原点逆时针旋转得到点,则点的坐标是,
故答案为;
(3)若点与点关于原点对称,则点的坐标是,
故答案为;
(4)将沿轴翻折得到点,则点的坐标是,
故答案为;
(5)分别联结、、,得到,
则的面积是:,
故答案为.
【点睛】
本题考查的是作图—旋转变换,掌握旋转变换的性质是解题的关键.
27.(1)垂线段最短;(2)存在,当,;当,;当,;当,.
【分析】
(1)利用垂线段最短即可得出结论;
(2)分类讨论,利用等腰三角形的判定可得出P点坐标,利用三角形面积公式得出结论.
【详解】
解:(1)∵在平面直角坐标系中,AO⊥BO,O为垂足,
∴AO表示A点到直线BO的距离,
∵,
∴,
∵垂线段最短,且不与O重合,
∴,即,
∴的理由是“垂线段最短”;
(2)在轴上存在点,使是等腰三角形,
①如图1,当P在B点左边,BP=BA=a,为等腰三角形,
∵,
∴,
∴;
②如图2,当P在B点右边,BP=BA=a,为等腰三角形,
∵,
∴,
∴;
③如图3,当P在B点右边,BP=AP,为等腰三角形,
此时P与O重合,即,
∵、,
∴,,
∴;
④如图4,当P在B点右边,AP=AB=a,为等腰三角形,
∵AO⊥BO,
∴O为PB中点,
∴,
∴,,
∴;
综上所述:在轴上存在点,使是等腰三角形,
当,;
当,;
当,;
当,;
【点睛】
本题主要考查了垂线段最短、坐标与图形、等腰三角形的判定与性质,分类讨论是解答此题的关键.
答案第1页,总2页
答案第1页,总2页
本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
2020-2021学年度上海市普陀区七年级下学期数学期末模拟卷
考试范围:12.1~15.2;考试时间:90分钟;
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题(共12分)
1.(本题2分)在实数,0,0.131131113…,中,属于无理数的是(
)
A.
B.0
C.0.131131113…
D.
2.(本题2分)要使式子有意义,则的取值范围是(
)
A.且
B.
C.
D.
3.(本题2分)如图,下列条件不能判断的是(
)
A.
B.
C.
D.
4.(本题2分)用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是(
)
A.SAS
B.AAS
C.ASA
D.SSS
5.(本题2分)若点
在轴上,则点在(
)
A.第一象限
B.第二象限
C.第三项县
D.第四象限
6.(本题2分)如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,
=15,DE=3,AB=6,则AC长是(
)
A.4
B.5
C.6
D.7
第II卷(非选择题)
二、填空题(共36分)
7.(本题3分)平方根等于其本身的实数是:__________.
8.(本题3分)化简:__________.
9.(本题3分)计算:____________.
10.(本题3分)近似数精确到__________位,有效数字是__________.
11.(本题3分)如图,,设,那么,,的关系式______.
12.(本题3分)如图,将纸片沿折叠,使点A落在点处,且平分,平分,若,则的度数是_______.
13.(本题3分)已知,如图,AB∥CD,AF∥DE,AF=DE,且BE=2,BC=10,则EF=________.
14.(本题3分)在平面直角坐标系中,点的坐标是,若直线平行于轴,且两点距离等于3,则点的坐标为____________.
15.(本题3分)如果一个等腰三角形的两条边长分别为3cm和6cm,那么第三条边的长是________cm.
16.(本题3分)如图,在中,和的平分线相交于点,过点作,分别交、于点、.若,,那么的周长为_______.
17.(本题3分)如图,如果将△ABC绕点A逆时针旋转40°得到△ADE,其中但D恰好落在BC边上,那么∠ADE=______.
18.(本题3分)如图,在平面直角坐标系中,第一次将
变换成,第二次将变换成,第三次将变换成,,将进行n次变换,得到,观察每次变换中三角形顶点坐标有何变化,找出规律,推测的坐标是______,的坐标是______.
三、解答题(共52分)
19.(本题5分)计算:
20.(本题5分)计算:
21.(本题5分)如图,已知直线AB、CD被直线EF所截,GE平分,GF平分,,ABCD吗?为什么?
答:
.
解:因为GE平分,GF平分(已知)
所以=2
.
=2
.(
)
所以+=
(等式性质)
因为(已知)
所以+=
.
所以ABCD(
).
22.(本题5分)如图,在△ABC
中,点
D、E
分别在
BC、AC
上且
BD=CE,AD=DE,
∠C
=∠ADE,
则∠B
=∠C,试填写说理过程.
解因为∠EDB
=∠C+∠DEC(
)
即∠ADB+∠ADE
=∠C+∠DEC
因为∠C
=∠ADE(
)
所以∠
=∠
(等式性质)
在△ABD
与△DCE
中,
所以△ABD
≌
△DCE(
)
所以∠B
=∠C(
)
23.(本题5分)如图,已知△ABC,请按下列要求作图:
(1)用直尺和圆规作△ABC的角平分线CG;
(2)作BC边上的高线(本小题作图工具不限);
(3)用直尺和圆规作△DEF,使△DEF≌△ABC.
24.(本题6分)如图,,,,且,求证:.
25.(本题6分)如图,在中,.点为边上一点,于点,点为上一点.连结并延长与相交于点,连结.已知.
(1)若平分,求证:≌.
(2)若,求的长.
(3)若,求的读数.
26.(本题7分)在直角坐标平面内,点的坐标如图所示.
(1)请写出点的坐标.
点的坐标是
;
点的坐标是
;
点的坐标是
;
(2)点点绕原点逆时针旋转得到点,则点的坐标是
;
(3)若点与点关于原点对称,则点的坐标是
;
(4)将沿x周翻折得到点,则点的坐标是
;
(5)分别联结,得到,则的面积是
.
27.(本题8分)如图,在直角坐标平面内有两点、,且、两点之间的距离等于(为大于0的已知数),在不计算的数值条件下,完成下列两题:
(1)以学过的知识用一句话说出的理由;
(2)在轴上是否存在点,使是等腰三角形,如果存在,请写出点的坐标,并求的面积;如果不存在,请说明理由.
试卷第2页,总2页
试卷第1页,总1页
参考答案
1.C
【分析】
无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【详解】
解:是分数,属于有理数;
0,均为整数,属于有理数;
0.131131113…是无限不循环小数,属于无理数;
故选:C
【点睛】
此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.
2.A
【分析】
根据使分式和二次根式有意义的条件即可解答.
【详解】
根据题意可知:
,
∴.
故选:A.
【点睛】
本题考查使分式和二次根式有意义的条件.掌握分母不能为0和被开方数大于等于0是解答本题的关键.
3.C
【分析】
根据平行线的判定进行判断求解.
【详解】
解:A.
,根据同旁内角互补,两直线平行,可判定,故此选项不符合题意;
B.
,根据内错角相等,两直线平行可判定,故此选项不符合题意;
C.
,根据内错角相等,两直线平行可判定,但不能判断,故此选项符合题意;
D.
,根据同位角相等,两直线平行可判定,故此选项不符合题意;
故选:C.
【点睛】
本题考查平行线的判定,掌握平行线的判定方法正确推理论证是解题关键.
4.D
【分析】
根据三角形全等的判定与性质即可得出答案.
【详解】
解:根据作法可知:OC=O′C′,OD=O′D′,DC=D′C′
∴△OCD≌△O′C′D′(SSS)
∴∠COD=∠C′O′D′
∴∠AOB=∠A′O′B′
故选D.
【点睛】
本题考查的是三角形全等,属于基础题型,需要熟练掌握三角形全等的判定与性质.
5.B
【分析】
根据x轴上点的坐标的特点y=0,计算出a的值,从而得出点Q坐标,并判断点Q所在的象限
【详解】
解:∵点P(a,a-1)在x轴上,
∴a-1=0,
∴a=1
∴a-2=-1,a+1=2
则点Q的坐标为(-1,2),
∴点Q在第二象限
故选:B
【点睛】
本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
6.A
【分析】
根据角平分线上的点到角的两边的距离相等可得AC边上的高,再利用S△ABD+S△ACD=S△ABC,即可得解.
【详解】
解:作DF⊥AC于F,如图:
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF=3,
∵S△ABD+S△ACD=S△ABC,
∴,
∴AC=4.
故选:A.
【点睛】
本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.
7.0
【分析】
根据平方的特性从三个特殊数0,±1中找,即可得到答案.
【详解】
解:∵02=0,
∴平方根等于本身的是0;
故答案是:0
【点睛】
本题考查了平方根的定义,这类问题要记准三个特殊的数:0,±1.
8.
【分析】
先判断两个实数的大小关系,再根据绝对值的代数意义化简,进而得出答案.
【详解】
解:∵,
∴原式
,
故答案为:.
【点睛】
此题主要考查了绝对值的代数意义,正确判断实数的大小是解题关键.
9.
【分析】
根据积的乘方公式和幂的乘方公式计算即可
【详解】
;故答案为.
【点睛】
本题考查了积的乘方公式和幂的乘方公式,解题的关键是理解积的乘方公式和幂的乘方公式.
10.千;
6,0
【分析】
根据近似数的精确度和有效数字的定义求解.
【详解】
近似数=60000,精确到千位,有2个有效数字,有效数字是6和0.
故答案为:千;6和0.
【点睛】
本题考查了近似数和有效数字,理解近似数和有效数字是解题的关键.
11.
【分析】
过作,过作,根据平行线的性质可知,然后根据平行线的性质即可求解;
【详解】
如图,过作,过作,
∴,
∴,,,
∵,
∴,
∴,
∴,
∴,
∴.
故答案为:.
【点睛】
本题考查了平行线的性质,两直线平行同位角相等,两直线平行内错角相等,正确理解平行线的性质是解题的关键;
12.60°
【分析】
连接AA′.首先求出∠BAC,再证明∠1+∠2=2∠BAC即可解决问题.
【详解】
解:连接AA′.
∵A'B平分∠ABC,A'C平分∠ACB,∠BA'C=105°,
∴∠A′BC+∠A′CB=75°,
∴∠ABC+∠ACB=150°,
∴∠BAC=180°-150°=30°,
∵∠1=∠DAA′+∠DA′A,∠2=∠EAA′+∠EA′A,
由折叠可知:∠DAA′=∠DA′A,∠EAA′=∠EA′A,
∴∠1+∠2=2(∠DAA′+∠EAA′)=2∠BAC=60°,
故答案为:60°.
【点睛】
本题考查三角形的内角和定理、角平分线的定义、三角形的外角的性质等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识,属于中考常考题型.
13.6
【分析】
首先证明△ABF≌△DCE,根据全等三角形的性质可得BF=CE,再根据等式的性质可得CF=EB=2,进而可得EF的长.
【详解】
∵AB∥CD,AF∥DE,
∴∠B=∠C,∠AFB=∠DEC,
在△ABF和△CDE中
,
∴△ABF≌△DCE(AAS),
∴BF=CE,
∴BF?EF=CE?EF,
即CF=EB=2,
∵BC=10,
∴EF=10?2?2=6,
故答案为6.
【点睛】
此题考查全等三角形的判定与性质,解题关键在于得到CF=EB=2.
14.或
【分析】
根据平行于轴的直线上的点纵坐标相等,得出点B的纵坐标为2,再根据两点距离等于3,用A点的横坐标加3或减3即可
【详解】
∵点的坐标是,直线平行于轴,
∴B点的纵坐标为2;
∵两点距离等于3,
∴B点的横坐标为-3+3=0或-3-3=-6
∴B或
故答案为:或
【点睛】
本题涉及到的知识点为:平行于y轴的直线上的点的横坐标相等;一条直线上到一个定点为定长的点有2个.
15.6
【分析】
分“3cm为腰长”和“6cm为腰长”两种情况计算,再根据三边关系判断即可.
【详解】
解:分两种情况考虑:
若3cm为等腰三角形的腰长,则三边分别为3cm,3cm,6cm,因为3+3=6,不符合三边关系,故舍去;
若6cm为等腰三角形的腰长,则三边分别为6cm,6cm,3cm,符合三边关系,则第三条边的长是6cm.
故答案为:6.
【点睛】
本题考查了等腰三角形的性质及三边关系,掌握基础知识是关键,做题时注意分情况考虑.
16.
【分析】
根据角平分线的性质,可得∠EBO与∠OBC的关系,∠FCO与∠OCB的关系,根据平行线的性质,可得∠DOB与∠BOC的关系,∠FOC与∠OCB的关系,根据等腰三角形的判定,可得OE与BE的关系,OE与CE的关系,根据三角形的周长公式,可得答案.
【详解】
∵∠ABC与∠ACB的平分线相交于点O,
∴∠EBO=∠OBC,∠FCO=∠OCB.
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠EOB=∠EBO,∠FOC=∠FCO,
∴EO=BE,OF=FC.
C△AEF=AE+EF+AF=AE+BE+AF+CF=AB+AC=9.
故答案为:9.
【点睛】
本题考查了等腰三角形的判定与性质,利用等腰三角形的判定与性质是解题关键,又利用了角平分线的性质,平行线的性质.
17.70°
【分析】
由将△ABC绕点A逆时针旋转40°得到△ADE,可得AB=AD,∠BAD=40°,继而求得∠B的度数,然后由旋转的性质,可求得∠ADE的度数.
【详解】
解:∵将△ABC绕点A逆时针旋转40°得到△ADE,
∴AB=AD,∠BAD=40°,
∴∠B=∠ADB=70°,
∴∠ADE=∠B=70°.
故答案为:70°.
【点睛】
此题考查了旋转的性质以及等腰三角形的性质.注意掌握旋转前后图形的对应关系是关键.
18.
【分析】
根据图形写出点A系列的坐标,根据具体数值找到规律即可.
【详解】
解:,
的横坐标为,纵坐标都为3,
,即
故答案为:;.
【点睛】
本题考查点坐标的规律,涉及乘方知识,是重要考点,难度较易,掌握相关知识是解题关键.
19.6
【分析】
直接利用二次根式的性质以及分数值数幂的性质、零指数幂的性质、负指数幂的性质分别化简得出答案.
【详解】
解:原式
=
=6.
【点睛】
本题主要考查了实数运算,正确化简各数是解题关键.
20.
【分析】
根据二次根式的乘法,绝对值的性质、负整指数幂的运算法则解题.
【详解】
解:原式=
=
=
.
【点睛】
本题考查实数的混合运算,是重要考点
,难度较易,掌握相关知识是解题关键.
21.见解析
【分析】
根据角平分线的定义和平行线的判定方法推理可得结论.
【详解】
解:平行,理由如下:
因为GE平分∠AEF,GF平分∠EFC(已知),
所以∠AEF=2∠1,
∠EFC=2∠2,(角平分线的定义)
所以∠AEF+∠EFC=2(∠1+∠2)(等式性质),
因为∠1+∠2=90°(已知),
所以∠AEF+∠EFC=180°,
所以AB∥CD(同旁内角互补,两直线平行).
【点睛】
本题考查了平行线的判定,牢记平行线的三个判定定理是解决此类题目的关键.
22.见详解
【分析】
利用三角形的外角等于不相邻的两个内角的和可证∠ADB=∠DEC.根据“SAS”
证得△ABD≌△DCE即可.
【详解】
解:∵∠EDB
=∠C+∠DEC(三角形的外角性质)
即∠ADB+∠ADE
=∠C+∠DEC
∵∠C
=∠ADE(已知)
∴∠ADB
=∠DEC(等式性质)
在△ABD
与△DCE
中,
∴△ABD
≌
△DCE(SAS)
∴∠B
=∠C(全等三角形的对应角相等)
【点睛】
此题考查了三角形的外角性质和全等三角形的性质和判定,解决本题的关键是熟练掌握相关知识.
23.见解析
【分析】
(1)利用基本作图(作已知角的平分线)画∠ACB的平分线OG;
(2)过点A作AH⊥BC于H,则AH为BC边上的高;
(3)先作线段EF=BC,然后分别以E、F为圆心,BA和CA为半径画弧,两弧交于点D,则△DEF与△ABC全等.
【详解】
解:(1)如图1,CG为所作;
(2)如图1,AH为所作;
(3)如图2,△DEF为所作.
【点睛】
本题考查了作图﹣复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
24.见解析
【分析】
先求出∠CAE=∠BAD再利用AAS证明△ABD≌△ACE,即可解答.
【详解】
证明:∵AB⊥AC,AD⊥AE,
∴∠BAE+∠CAE=90°,∠BAE+∠BAD=90°,
∴∠CAE=∠BAD,
又AB=AC,,
∴△ABD≌△ACE(AAS),
∴.
【点睛】
此题考查全等三角形的判定与性质,解题关键在于判定三角形全等.
25.(1)见解析;(2)2;(3)40°
【分析】
(1)利用角平分线的定义及AAS定理证明三角形全等;
(2)根据等腰三角形的判定和性质求解;
(3)解法一:结合等边对等角,角平分线的定义及三角形内角和定理计算求解;
解法二:利用圆周角定理求解.
【详解】
解:(1)证明:∵,
∴,
∵,
∴.
∵平分,
∴.
又∵,
∴≌(AAS).
(2)∵在中,,
∴,.
∵,
∴,
∴.
∴在中,.
(3)解法一:∵,
∴.
∵,
∴
.
∴.
解法二:∵,
∴点,,,在以点为圆心的圆上,
∴,
∴.
【点睛】
本题考查全等三角形的判定和性质,等腰三角形的判定和性质,也考查圆周角定理,掌握相关性质定理正确推理计算是解题关键.
26.(1);;;(2);(3);(4);(5)
【分析】
(1)根据在坐标系所处的位置即可得到点的坐标;
(2)根据旋转的性质即可求得点的坐标;
(3)根据中心对称的性质即可求得点的坐标;
(4)根据轴对称的性质即可求得点的坐标;
(5)的面积由正方形的面积减去两个三角形的面积求得即可.
【详解】
解:(1)在直角坐标平面内,点、、的坐标如图所示:
点的坐标是;点的坐标是;点的坐标是,
故答案为;;.
(2)将点绕原点逆时针旋转得到点,则点的坐标是,
故答案为;
(3)若点与点关于原点对称,则点的坐标是,
故答案为;
(4)将沿轴翻折得到点,则点的坐标是,
故答案为;
(5)分别联结、、,得到,
则的面积是:,
故答案为.
【点睛】
本题考查的是作图—旋转变换,掌握旋转变换的性质是解题的关键.
27.(1)垂线段最短;(2)存在,当,;当,;当,;当,.
【分析】
(1)利用垂线段最短即可得出结论;
(2)分类讨论,利用等腰三角形的判定可得出P点坐标,利用三角形面积公式得出结论.
【详解】
解:(1)∵在平面直角坐标系中,AO⊥BO,O为垂足,
∴AO表示A点到直线BO的距离,
∵,
∴,
∵垂线段最短,且不与O重合,
∴,即,
∴的理由是“垂线段最短”;
(2)在轴上存在点,使是等腰三角形,
①如图1,当P在B点左边,BP=BA=a,为等腰三角形,
∵,
∴,
∴;
②如图2,当P在B点右边,BP=BA=a,为等腰三角形,
∵,
∴,
∴;
③如图3,当P在B点右边,BP=AP,为等腰三角形,
此时P与O重合,即,
∵、,
∴,,
∴;
④如图4,当P在B点右边,AP=AB=a,为等腰三角形,
∵AO⊥BO,
∴O为PB中点,
∴,
∴,,
∴;
综上所述:在轴上存在点,使是等腰三角形,
当,;
当,;
当,;
当,;
【点睛】
本题主要考查了垂线段最短、坐标与图形、等腰三角形的判定与性质,分类讨论是解答此题的关键.
答案第1页,总2页
答案第1页,总2页
同课章节目录
