3.1独立性检验课件(共27张PPT-2020-2021学年高二下学期苏教版选修2-3第三章第一节
文档属性
| 名称 | 3.1独立性检验课件(共27张PPT-2020-2021学年高二下学期苏教版选修2-3第三章第一节 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-23 17:05:31 | ||
图片预览




文档简介
3.1 独立性检验
高中数学 选修2-2
分类变量的取值可以用____ _表示.
知识点一 分类变量
实数
对于性别变量,其取值为男和女两种.
♂
♀
这种变量的不同“值”表示个体所属的不同类别,像这类变量称为分类变量.
生活中的分类变量
是否吸烟,宗教信仰,国籍…
两个分类变量之间是否有关系
性别
是否喜欢数学课程
吸烟
患肺癌
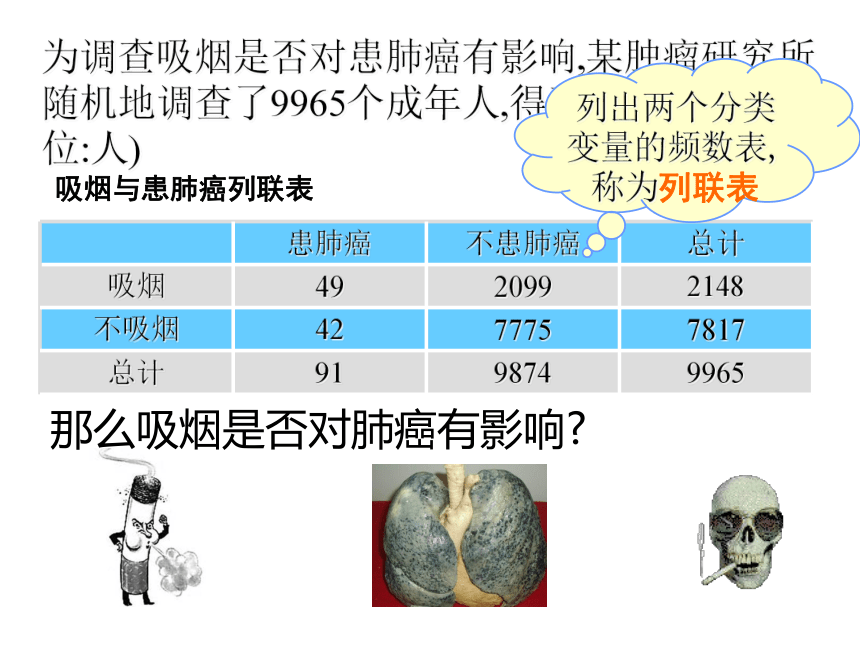
为调查吸烟是否对患肺癌有影响,某肿瘤研究所随机地调查了9965个成年人,得到如下结果(单位:人)
患肺癌
不患肺癌
总计
吸烟
49
2099
2148
不吸烟
42
7775
7817
总计
91
9874
9965
那么吸烟是否对肺癌有影响?
吸烟与患肺癌列联表
列出两个分类变量的频数表,称为列联表
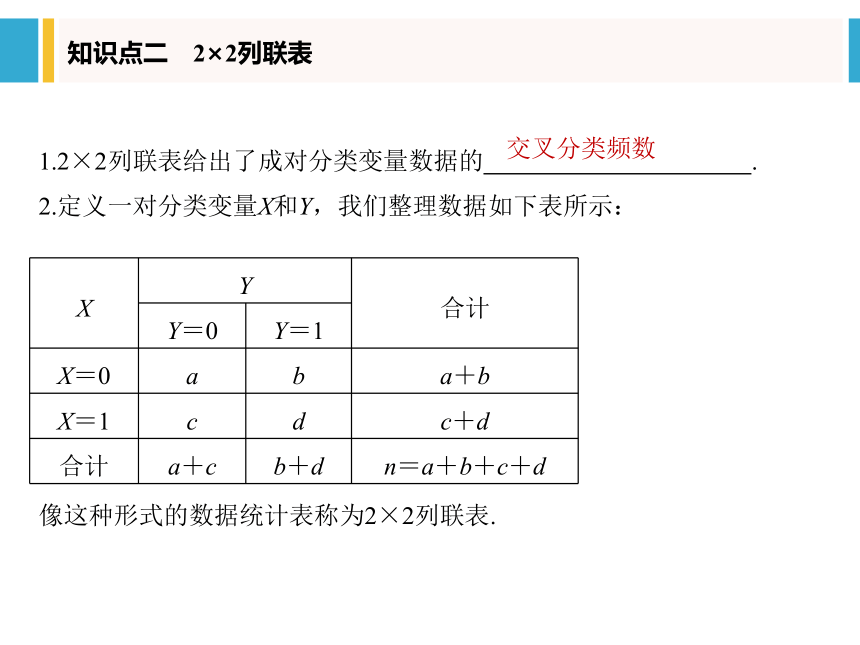
知识点二 2×2列联表
1.2×2列联表给出了成对分类变量数据的 .
2.定义一对分类变量X和Y,我们整理数据如下表所示:
X
Y
合计
Y=0
Y=1
X=0
a
b
a+b
X=1
c
d
c+d
合计
a+c
b+d
n=a+b+c+d
像这种形式的数据统计表称为2×2列联表.
交叉分类频数
患肺癌
不患肺癌
总计
吸烟
49
2099
2148
不吸烟
42
7775
7817
总计
91
9874
9965
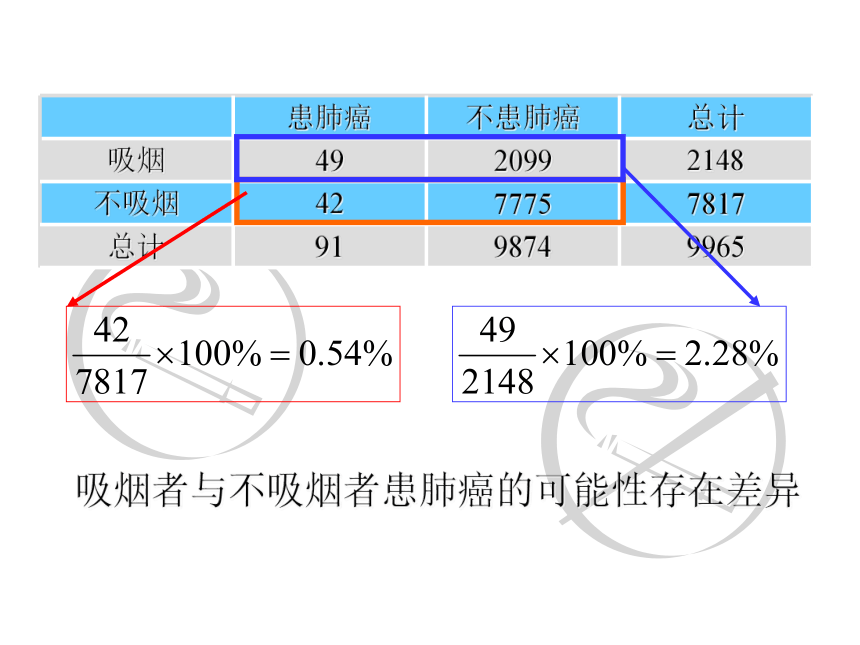
吸烟者与不吸烟者患肺癌的可能性存在差异
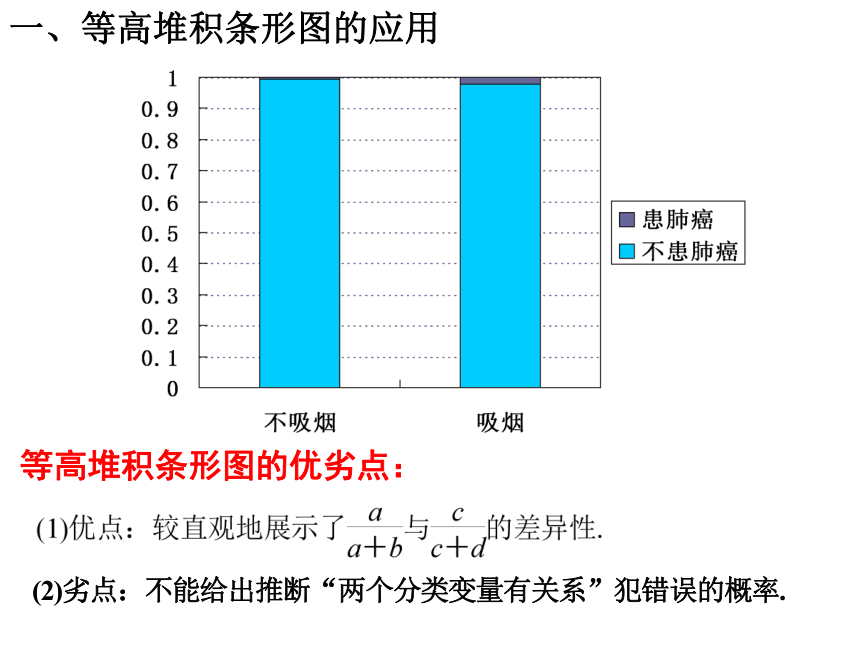
一、等高堆积条形图的应用
等高堆积条形图的优劣点:
(2)劣点:不能给出推断“两个分类变量有关系”犯错误的概率.
从上面数据和图形可以看出吸烟和患肺癌有关
从上面数据和图形可以看出吸烟和患肺癌有关
事实确是如此!
我们能够有多大的把握认为“吸烟与患肺癌有关”?
吸烟
患肺癌
若将事件“某成年人吸烟”记为 ,将事件“某成年人患肺癌”记为 ,则事件“某成年人不吸烟”为 ,事件“某成年人不患肺癌”记为 ,这样回答“患肺癌与吸烟是否有关?
其实就是需要回答“事件 与事件 是否独立?
吸烟与患肺癌列联表
患肺癌
不患肺癌
总计
吸烟
a
b
a+b
不吸烟
c
d
c+d
总计
a+c
b+d
a+b+c+d
假设
H0:吸烟与患肺癌没有关系
P(AB)=P(A)P(B)
假设H0:吸烟和患肺癌之间没有关系
吸烟且患肺癌人数
吸烟但未患肺癌人数
不吸烟但患肺癌人数
不吸烟且未患肺癌人数
如果实际观测值与由事件A和B相互独立的假设的估计值相差不“大”,那么,我们就可以认为这些差异是由随机误差造成的,假设H0不能被所给数据否定.
否则,应认为假设H0不能接受.
怎样描述实际观测值与估计值的差异呢?
统计学中采用
即
(n=a+b+c+d)
根据前面数据
若H0成立
应该很小
99%把握认
为A与B有关
P(χ≥x0)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
x0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
0.1%把握认为A与B无关
1%把握认为A与B无关
99.9%把握认为A与B有关
90%把握认
为A与B有关
10%把握认为A与B无关
没有充分的依据显示A与B有关,但也不能做出结论A与B无关
例如
统计学家已有明确的结论:在 成立的条件下
6.635
远大于
99%的把握认为“吸烟与患肺癌有关系”
利用统计量 来确定在多大程度上可以认为“两个分类变量有关系”的方法称为两个分类变量的独立性检验.用这种方法还可以解决类似的问题,如花的颜色与花粉的形状是否相关、用药效果与用药方式是否相关等.
上述进行独立性检验所采用的思想是:
要研究“患肺癌与吸烟有关”这一结论的可靠程度,先假设该结论不成立,即假设“患肺癌与吸烟没有关系”成立 , 在该假设下构造 统计量.如果
的观测值很大,那么在一定程度上说明假设不合理.根据 的含义,可以通过 评价该假设不合理的程度.如果计算出 ,那么说明假设不合理的程度约为99%, “即患肺癌与吸烟有关系”这一结论成立的可信程度约为
99%.
知识点三 独立性检验
1.定义:利用χ2的取值推断分类变量X和Y 的方法称为χ2独立性检验,读作“卡方独立性检验”.简称独立性检验.
2.χ2= ,其中n=a+b+c+d.
3.独立性检验解决实际问题的主要环节
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算χ2的值,并与临界值xα比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
是否独立
命题角度1 有关“相关的检验”
例2 某校对学生课外活动进行调查,结果整理成下表:试根据小概率值α=0.005的独立性检验,分析喜欢体育还是文娱与性别是否有关系.
二、由χ2进行独立性检验
性别
喜欢
合计
体育
文娱
男生
21
23
44
女生
6
29
35
合计
27
52
79
解 零假设为H0:喜欢体育还是喜欢文娱与性别没有关系.
∵a=21,b=23,c=6,d=29,n=79,
根据小概率值α=0.005的独立性检验,我们推断H0不成立,即认为喜欢体育还是喜欢文娱与性别有关.
反思感悟
用χ2进行“相关的检验”步骤
(1)零假设:即先假设两变量间没关系.
(2)计算χ2:套用χ2的公式求得χ2值.
(3)查临界值:结合所给小概率值α查得相应的临界值xα.
(4)下结论:比较χ2与xα的大小,并作出结论.
命题角度2 有关“无关的检验”
例3 下表是某届某校本科志愿报名时,对其中304名学生进入高校时是否知道想学专业的调查表:
?
知道想学专业
不知道想学专业
合计
男生
63
117
180
女生
42
82
124
合计
105
199
304
根据表中数据,则下列说法正确的是____.(填序号)
①性别与知道想学专业有关;
②性别与知道想学专业无关;
③女生比男生更易知道所学专业.
②
所以性别与知道想学专业无关.
反思感悟
独立性检验解决实际问题的主要环节
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算χ2的值,并与临界值xα比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
跟踪训练3 某省进行高中新课程改革,为了解教师对新课程教学模式的使用情况,某一教育机构对某学校的教师关于新课程教学模式的使用情况进行了问卷调查,共调查了50人,其中有老教师20人,青年教师30人.老教师对新课程教学模式赞同的有10人,不赞同的有10人;青年教师对新课程教学模式赞同的有24人,不赞同的有6人.
(1)根据以上数据建立一个2×2列联表;
解 2×2列联表如下表所示:
教师年龄
对新课程教学模式
合计
赞同
不赞同
老教师
10
10
20
青年教师
24
6
30
合计
34
16
50
(2)试根据小概率值α=0.01的独立性检验,分析对新课程教学模式的赞同情况与教师年龄是否有关系.
解 零假设为H0:对新课程教学模式的赞同情况与教师年龄无关.
≈4.963<6.635=x0.01,
根据小概率值α=0.01的独立性检验,没有充分证据推断H0不成立,
即认为对新课程教学模式的赞同情况与教师年龄无关.
1.知识清单:
(1)分类变量.
(2)2×2列联表.
(3)等高堆积条形图.
(4)独立性检验,χ2公式.
2.方法归纳:数形结合.
3.常见误区:对独立性检验的原理不理解,导致不会用χ2分析问题.
课堂小结
高中数学 选修2-2
分类变量的取值可以用____ _表示.
知识点一 分类变量
实数
对于性别变量,其取值为男和女两种.
♂
♀
这种变量的不同“值”表示个体所属的不同类别,像这类变量称为分类变量.
生活中的分类变量
是否吸烟,宗教信仰,国籍…
两个分类变量之间是否有关系
性别
是否喜欢数学课程
吸烟
患肺癌
为调查吸烟是否对患肺癌有影响,某肿瘤研究所随机地调查了9965个成年人,得到如下结果(单位:人)
患肺癌
不患肺癌
总计
吸烟
49
2099
2148
不吸烟
42
7775
7817
总计
91
9874
9965
那么吸烟是否对肺癌有影响?
吸烟与患肺癌列联表
列出两个分类变量的频数表,称为列联表
知识点二 2×2列联表
1.2×2列联表给出了成对分类变量数据的 .
2.定义一对分类变量X和Y,我们整理数据如下表所示:
X
Y
合计
Y=0
Y=1
X=0
a
b
a+b
X=1
c
d
c+d
合计
a+c
b+d
n=a+b+c+d
像这种形式的数据统计表称为2×2列联表.
交叉分类频数
患肺癌
不患肺癌
总计
吸烟
49
2099
2148
不吸烟
42
7775
7817
总计
91
9874
9965
吸烟者与不吸烟者患肺癌的可能性存在差异
一、等高堆积条形图的应用
等高堆积条形图的优劣点:
(2)劣点:不能给出推断“两个分类变量有关系”犯错误的概率.
从上面数据和图形可以看出吸烟和患肺癌有关
从上面数据和图形可以看出吸烟和患肺癌有关
事实确是如此!
我们能够有多大的把握认为“吸烟与患肺癌有关”?
吸烟
患肺癌
若将事件“某成年人吸烟”记为 ,将事件“某成年人患肺癌”记为 ,则事件“某成年人不吸烟”为 ,事件“某成年人不患肺癌”记为 ,这样回答“患肺癌与吸烟是否有关?
其实就是需要回答“事件 与事件 是否独立?
吸烟与患肺癌列联表
患肺癌
不患肺癌
总计
吸烟
a
b
a+b
不吸烟
c
d
c+d
总计
a+c
b+d
a+b+c+d
假设
H0:吸烟与患肺癌没有关系
P(AB)=P(A)P(B)
假设H0:吸烟和患肺癌之间没有关系
吸烟且患肺癌人数
吸烟但未患肺癌人数
不吸烟但患肺癌人数
不吸烟且未患肺癌人数
如果实际观测值与由事件A和B相互独立的假设的估计值相差不“大”,那么,我们就可以认为这些差异是由随机误差造成的,假设H0不能被所给数据否定.
否则,应认为假设H0不能接受.
怎样描述实际观测值与估计值的差异呢?
统计学中采用
即
(n=a+b+c+d)
根据前面数据
若H0成立
应该很小
99%把握认
为A与B有关
P(χ≥x0)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
x0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
0.1%把握认为A与B无关
1%把握认为A与B无关
99.9%把握认为A与B有关
90%把握认
为A与B有关
10%把握认为A与B无关
没有充分的依据显示A与B有关,但也不能做出结论A与B无关
例如
统计学家已有明确的结论:在 成立的条件下
6.635
远大于
99%的把握认为“吸烟与患肺癌有关系”
利用统计量 来确定在多大程度上可以认为“两个分类变量有关系”的方法称为两个分类变量的独立性检验.用这种方法还可以解决类似的问题,如花的颜色与花粉的形状是否相关、用药效果与用药方式是否相关等.
上述进行独立性检验所采用的思想是:
要研究“患肺癌与吸烟有关”这一结论的可靠程度,先假设该结论不成立,即假设“患肺癌与吸烟没有关系”成立 , 在该假设下构造 统计量.如果
的观测值很大,那么在一定程度上说明假设不合理.根据 的含义,可以通过 评价该假设不合理的程度.如果计算出 ,那么说明假设不合理的程度约为99%, “即患肺癌与吸烟有关系”这一结论成立的可信程度约为
99%.
知识点三 独立性检验
1.定义:利用χ2的取值推断分类变量X和Y 的方法称为χ2独立性检验,读作“卡方独立性检验”.简称独立性检验.
2.χ2= ,其中n=a+b+c+d.
3.独立性检验解决实际问题的主要环节
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算χ2的值,并与临界值xα比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
是否独立
命题角度1 有关“相关的检验”
例2 某校对学生课外活动进行调查,结果整理成下表:试根据小概率值α=0.005的独立性检验,分析喜欢体育还是文娱与性别是否有关系.
二、由χ2进行独立性检验
性别
喜欢
合计
体育
文娱
男生
21
23
44
女生
6
29
35
合计
27
52
79
解 零假设为H0:喜欢体育还是喜欢文娱与性别没有关系.
∵a=21,b=23,c=6,d=29,n=79,
根据小概率值α=0.005的独立性检验,我们推断H0不成立,即认为喜欢体育还是喜欢文娱与性别有关.
反思感悟
用χ2进行“相关的检验”步骤
(1)零假设:即先假设两变量间没关系.
(2)计算χ2:套用χ2的公式求得χ2值.
(3)查临界值:结合所给小概率值α查得相应的临界值xα.
(4)下结论:比较χ2与xα的大小,并作出结论.
命题角度2 有关“无关的检验”
例3 下表是某届某校本科志愿报名时,对其中304名学生进入高校时是否知道想学专业的调查表:
?
知道想学专业
不知道想学专业
合计
男生
63
117
180
女生
42
82
124
合计
105
199
304
根据表中数据,则下列说法正确的是____.(填序号)
①性别与知道想学专业有关;
②性别与知道想学专业无关;
③女生比男生更易知道所学专业.
②
所以性别与知道想学专业无关.
反思感悟
独立性检验解决实际问题的主要环节
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算χ2的值,并与临界值xα比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
跟踪训练3 某省进行高中新课程改革,为了解教师对新课程教学模式的使用情况,某一教育机构对某学校的教师关于新课程教学模式的使用情况进行了问卷调查,共调查了50人,其中有老教师20人,青年教师30人.老教师对新课程教学模式赞同的有10人,不赞同的有10人;青年教师对新课程教学模式赞同的有24人,不赞同的有6人.
(1)根据以上数据建立一个2×2列联表;
解 2×2列联表如下表所示:
教师年龄
对新课程教学模式
合计
赞同
不赞同
老教师
10
10
20
青年教师
24
6
30
合计
34
16
50
(2)试根据小概率值α=0.01的独立性检验,分析对新课程教学模式的赞同情况与教师年龄是否有关系.
解 零假设为H0:对新课程教学模式的赞同情况与教师年龄无关.
≈4.963<6.635=x0.01,
根据小概率值α=0.01的独立性检验,没有充分证据推断H0不成立,
即认为对新课程教学模式的赞同情况与教师年龄无关.
1.知识清单:
(1)分类变量.
(2)2×2列联表.
(3)等高堆积条形图.
(4)独立性检验,χ2公式.
2.方法归纳:数形结合.
3.常见误区:对独立性检验的原理不理解,导致不会用χ2分析问题.
课堂小结
