小学数学西师大版六年级下 3.3反比例 课件(11页ppt)
文档属性
| 名称 | 小学数学西师大版六年级下 3.3反比例 课件(11页ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-22 20:02:56 | ||
图片预览



文档简介
反比例的意义
笔记本的单价3元/本
复习引入
购买的数量(本)
......
总价(元)
......
笔记本总价与购买的数量之间有什么关系?它们成什么比例?
正比例的特征:
1,有两种相关联的量。
2,变化有规律。
3,两种相关联的量比值一定。
1
2
3
5
8
3
6
9
15
24
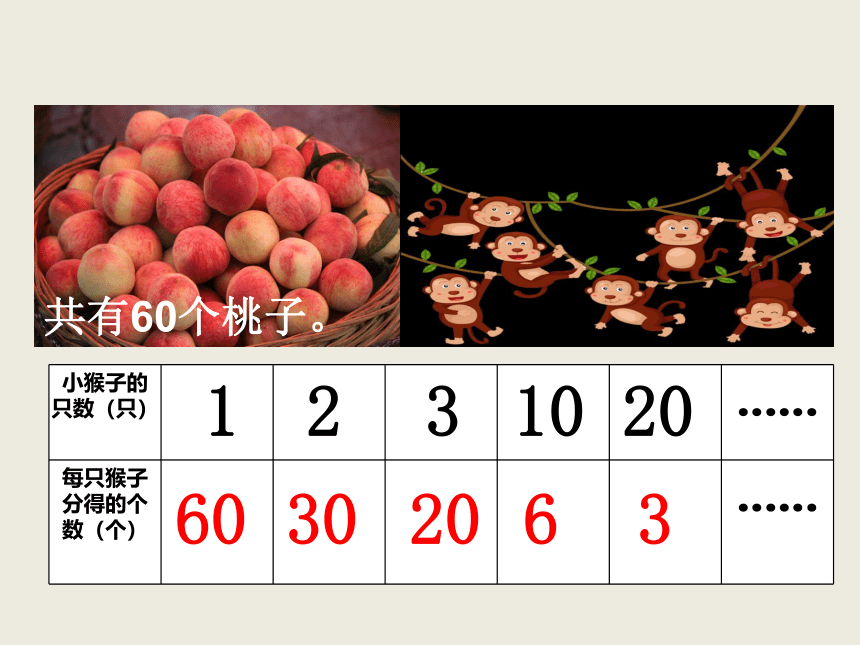
共有60个桃子。
小猴子的只数(只)
......
每只猴子分得的个数(个)
......
1
2
3
10
20
60
30
20
6
3
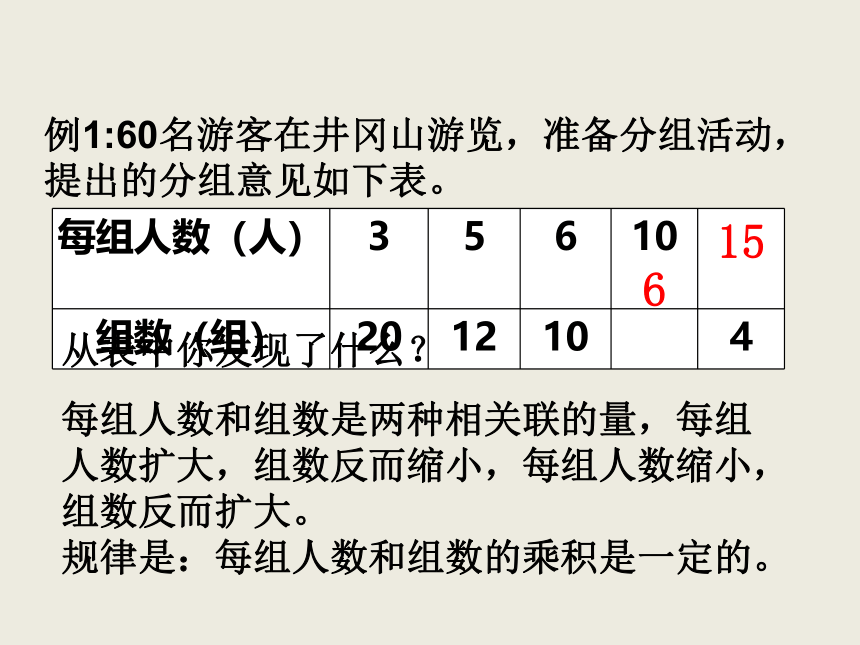
例1:60名游客在井冈山游览,准备分组活动,提出的分组意见如下表。
每组人数(人)
3
5
6
10
组数(组)
20
12
10
4
从表中你发现了什么?
每组人数和组数是两种相关联的量,每组人数扩大,组数反而缩小,每组人数缩小,组数反而扩大。
规律是:每组人数和组数的乘积是一定的。
6
15
试一试:探索规律并完成表格。
这篇稿子如果每分打120个字,20分可以打完。
每分打字个数(个)
120
100
75
60
所需时间(分)
25
30
60
每分钟打的字数和所用的时间是( )。
每分钟打字的数量( ),所用的时间( )。
每分钟打字的( ),所用的时间( )。
每分钟打字的数量和所用的时间( )。
40
50
50
两个相关的量
扩大
反而缩小
数量缩小
反而扩大
乘积一定
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
每组人数×组数=游客总人数 (积一定)
每分钟打的字数×时间=稿件总字数(积一定)
课堂探索
从上面两个例子中你发现了什么?
正比例:
反比例:
怎么样区分正反比例?
1、正比例是一个量扩大另一个量也随
之扩大。
2、两个相关联的量比值一定。
1、反比例是一个量扩大另一个量随之
缩小。
2、两个相关联的量乘积一定。
在括号里选填“正”“反”或“不成”。
1、速度一定,路程和时间成( )比例;
路程一定,速度和时间成( )比例;
时间一定,路程和速度( )比例。
2、工作效率一定,工作总量和工作时间成( )比例;
工作时间一定,工作效率和工作总量成( )比例;
工作总量一定,工作效率和工作时间成( )比例。
课堂练习:
正
反
正
正
正
反
判断下面各题中的两种量是否比例。如成比例,成什么比例?
(1)报纸的单价一定,订阅的份数与总价。
(2)圆柱的体积一定,它的底面积和高
(3)运动员跳高的高度和他的身高。
(4)一筐桃平均分给猴子,猴的只数和每只猴分桃的个数。
(5)圆的面积和它的半径。
(6)C =4a,C 和a。
(成反比例)
(成反比例)
(成正比例)
(不成比例)
(成正比例)
课堂练习
(不成比例)
三、选择题。
1、下列各种量中成反比例的是( )
A、同时同地的竿高和影长
B、正方形的周长和面积
C、积一定,两个因数
2、xy+2=k(k一定),x和y( )
A、成正比例 B、不成比例 C、成反比例
3、如果y=10x,x和y( )
A、成正比例 B、成反比例 C、不成比例
4、完成一项工程,如果工作效率相同,那么参加人数与需要的天数( )
A、成正比例 B、成反比例 C、不成比例
C
B
A
B
通过本课的学习你有什么收获?
课堂总结
笔记本的单价3元/本
复习引入
购买的数量(本)
......
总价(元)
......
笔记本总价与购买的数量之间有什么关系?它们成什么比例?
正比例的特征:
1,有两种相关联的量。
2,变化有规律。
3,两种相关联的量比值一定。
1
2
3
5
8
3
6
9
15
24
共有60个桃子。
小猴子的只数(只)
......
每只猴子分得的个数(个)
......
1
2
3
10
20
60
30
20
6
3
例1:60名游客在井冈山游览,准备分组活动,提出的分组意见如下表。
每组人数(人)
3
5
6
10
组数(组)
20
12
10
4
从表中你发现了什么?
每组人数和组数是两种相关联的量,每组人数扩大,组数反而缩小,每组人数缩小,组数反而扩大。
规律是:每组人数和组数的乘积是一定的。
6
15
试一试:探索规律并完成表格。
这篇稿子如果每分打120个字,20分可以打完。
每分打字个数(个)
120
100
75
60
所需时间(分)
25
30
60
每分钟打的字数和所用的时间是( )。
每分钟打字的数量( ),所用的时间( )。
每分钟打字的( ),所用的时间( )。
每分钟打字的数量和所用的时间( )。
40
50
50
两个相关的量
扩大
反而缩小
数量缩小
反而扩大
乘积一定
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
每组人数×组数=游客总人数 (积一定)
每分钟打的字数×时间=稿件总字数(积一定)
课堂探索
从上面两个例子中你发现了什么?
正比例:
反比例:
怎么样区分正反比例?
1、正比例是一个量扩大另一个量也随
之扩大。
2、两个相关联的量比值一定。
1、反比例是一个量扩大另一个量随之
缩小。
2、两个相关联的量乘积一定。
在括号里选填“正”“反”或“不成”。
1、速度一定,路程和时间成( )比例;
路程一定,速度和时间成( )比例;
时间一定,路程和速度( )比例。
2、工作效率一定,工作总量和工作时间成( )比例;
工作时间一定,工作效率和工作总量成( )比例;
工作总量一定,工作效率和工作时间成( )比例。
课堂练习:
正
反
正
正
正
反
判断下面各题中的两种量是否比例。如成比例,成什么比例?
(1)报纸的单价一定,订阅的份数与总价。
(2)圆柱的体积一定,它的底面积和高
(3)运动员跳高的高度和他的身高。
(4)一筐桃平均分给猴子,猴的只数和每只猴分桃的个数。
(5)圆的面积和它的半径。
(6)C =4a,C 和a。
(成反比例)
(成反比例)
(成正比例)
(不成比例)
(成正比例)
课堂练习
(不成比例)
三、选择题。
1、下列各种量中成反比例的是( )
A、同时同地的竿高和影长
B、正方形的周长和面积
C、积一定,两个因数
2、xy+2=k(k一定),x和y( )
A、成正比例 B、不成比例 C、成反比例
3、如果y=10x,x和y( )
A、成正比例 B、成反比例 C、不成比例
4、完成一项工程,如果工作效率相同,那么参加人数与需要的天数( )
A、成正比例 B、成反比例 C、不成比例
C
B
A
B
通过本课的学习你有什么收获?
课堂总结
