河南省郑州市2020-2021学年高二下学期期末数学文科试题(Word含答案)
文档属性
| 名称 | 河南省郑州市2020-2021学年高二下学期期末数学文科试题(Word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-23 00:09:09 | ||
图片预览




文档简介
郑州市2020—2021学年下期期末考试
高二数学(文)试题
注意事项:
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.考试时间120分钟,满分150分.考生应首先阅读答题卡上的文字信息,然后在答题卡上作答,在试题卷上作答无效.交卷时只交答题卡.
参考公式和数据:
1.对于一组具有线性相关关系的数据,其回归直线的斜率和截距的最小二乘估计分别为:,;
2.,;
3.参考数据:
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.在用反证法证明命题“已知,,且.求证:,中至少有一个小于4”时,假设正确的是(
)
A.假设,都不大于
B.假设,都不小于
C.假设,都小于
D.假设,都大于
2.如图,复平面内的点对应的复数记为,则对应的点位于(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.中国茶文化博大精深,茶水的口感与茶叶的类型和水的温度有关某数学建模小组建立了茶水冷却时间和茶水温度的一组数据.经过分析,提出了四种回归模型,①②③④四种模型的残差平方和的值分别是,,,.则拟合效果最好的模型是(
)
A.模型①
B.模型②
C.模型③
D.模型④
4.(选修4-4:坐标系与参数方程)将曲线变换为曲线的一个伸缩变换为(
)
A.
B.
C.
D.
(选修4-5:不等式选讲)若关于的不等式的解集为空集,则实数的取值范围是(
)
A.
B.
C.
D.
5.已知糖水中含有糖,若再添加糖完全溶解在其中,则糖水变得更甜了(即糖水中含糖浓度变大).根据这个事实,下列不等式中一定成立的是(
)
A.
B.
C.
D.
6.“关注夕阳,爱老敬老”,某商会从2016年开始向晚晴山庄养老院捐赠物资和现金.下表记录了第年(2016年为第一年)捐赠现金(万元)的数据情况.由表中数据得到了关于的线性回归方程为,预测2021年该商会捐赠现金______万元.
A.
B.
C.
D.
7.若输出的的值等于,那么在程序框图中的判断框内应填写的条件是(
)
A.
B.
C.
D.
8.已知正数,满足,则的最小值为(
)
A.
B.
C.
D.
9.任何一个复数都可以表示成的形式,我们把叫做复数的三角形式.已知,则下列结论正确的是(
)
A.的实部为
B.
C.
D.
10.(选修4-4:坐标系与参数方程)已知曲线的参数方程(为参数,且).若以下曲线中有一个是,则曲线是(
)
A.
B.
C.
D.
(选修4-5:不等式选讲)已知,若恒成立,则的最大值为(
)
A.
B.
C.
D.
11.胡夫金字塔的形状为正四棱锥.1859年,英国作家约翰·泰勒在其《大金字塔》一书中提出:埃及人在建造胡夫金字塔时利用了黄金比例,泰勒还引用了古希腊历史学家希罗多德的记载:胡夫金字塔的每一个侧面的面积都等于金字塔高的平方,如图,即.已知四棱锥底面是边长约为英尺的正方形,顶点的投影在底面中心,为中点,根据以上条件,的长度(单位:英尺)约为(
)
A.
B.
C.
D.
12.已知,若,则与的大小关系为(
)
A.
B.
C.
D.不确定
第Ⅱ卷(非选择题,共90分)
二、填空题:本题共4小题,每小题5分,共20分.
13.若为方程(,)的一个根,则______.
14.从某大学随机选择名女大学生,其身高和体重数据如表所示:
身高()
体重()
根据表中的数据可得回归直线方程,,这表明女大学生的体重差异有______是由身高引起的.
15.在等差数列中,若,则(,).类比上述性质,在等比数列中,若,则存在的等式为______.
16.已知函数有五个不同的零点,且所有零点之和为,则实数的值为______.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.为复平面内的平行四边形,向量对应的复数为,对应的复数为,对应的复数为.
(Ⅰ)求点对应的复数;
(Ⅱ)判断、、、四点是否在同一个圆上?并证明你的结论.
18.(选修4-4:坐标系与参数方程)在平面直角坐标系中,以坐标原点为极点,轴的非负半轴为极轴且取相同的单位长度建立板坐标系,已知曲线的极坐标方程为;直线的倾斜角为,且经过曲线的左顶点.
(Ⅰ)求曲线的直角坐标方程和直线的参数方程;
(Ⅱ)求曲线的内接矩形的周长的最大值.
(选修4-5:不等式选讲)已知函数.
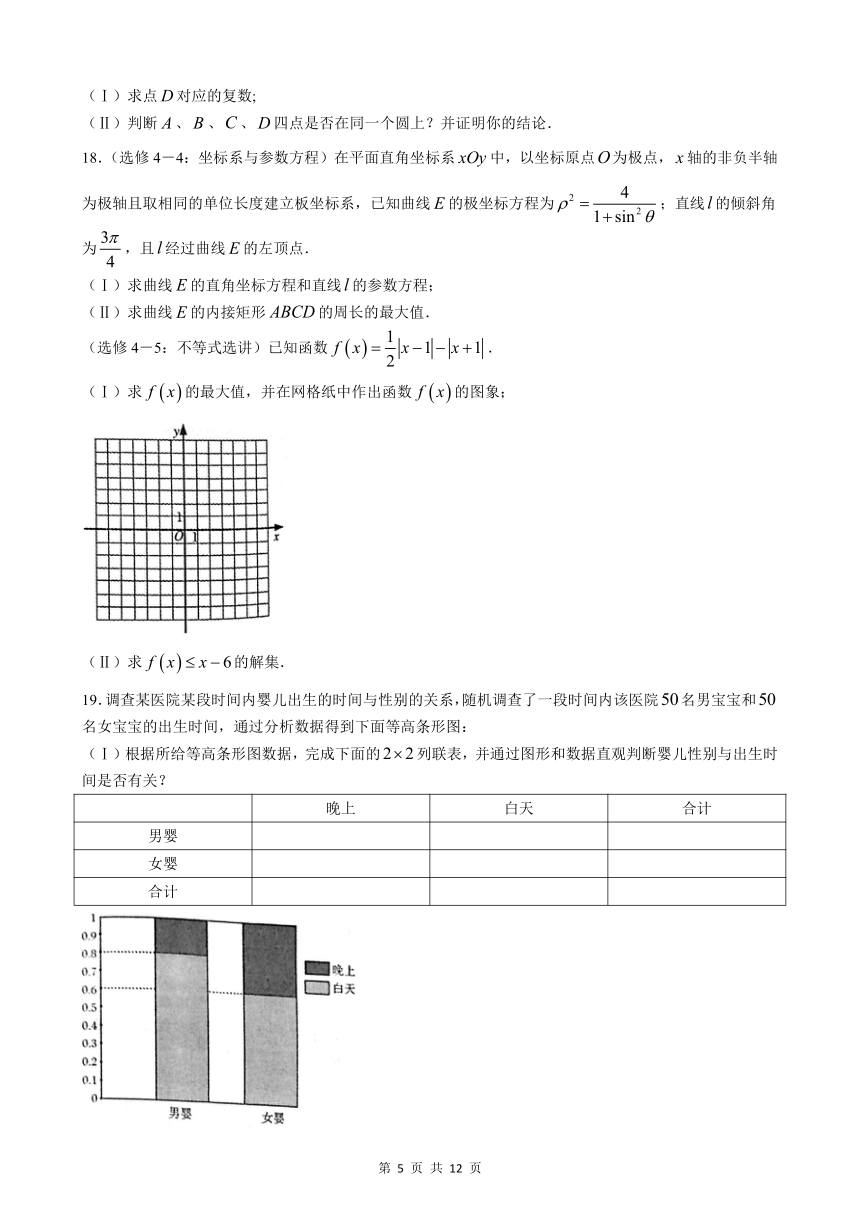
(Ⅰ)求的最大值,并在网格纸中作出函数的图象;
(Ⅱ)求的解集.
19.调查某医院某段时间内婴儿出生的时间与性别的关系,随机调查了一段时间内该医院名男宝宝和名女宝宝的出生时间,通过分析数据得到下面等高条形图:
(Ⅰ)根据所给等高条形图数据,完成下面的列联表,并通过图形和数据直观判断婴儿性别与出生时间是否有关?
晚上
白天
合计
男婴
女婴
合计
(Ⅱ)根据(Ⅰ)中列联表,能否在犯错误概率不超过的前提下认为婴儿的性别与出生的时间有关?
20.(选修4-4:坐标系与参数方程)平面直角坐标系中,射线:,曲线的参数方程为(为参数);以原点为极点,轴的非负半轴为极轴建立极坐标系,曲线的极坐标方程为.
(Ⅰ)写出射线的极坐标方程、曲线的普通方程;
(Ⅱ)已知射线与交于点,与交于点(异于点),求的值.
(选修4-5:不等式选讲)已知函数.
(Ⅰ)当时,求不等式的解集;
(Ⅱ)是否存在实数使得的解集中包含.若存在,求的取值范围;若不存在,说明理由.
21.红铃虫是棉花的主要害虫之一,其产卵数与温度有关.现收集到一只红铃虫的产卵数(个)和温度()的组观测数据,制成图1所示的散点图现用两种模型①(,),②分别进行拟合,由此得到相应的回归方程并进行残差分析,进一步得到图2所示的残差图.
根据收集到的数据,计算得到如下值:
表中;;;.
(Ⅰ)根据残差图,比较模型①、②的拟合效果,应选择哪个模型?并说明理由;
(Ⅱ)根据(Ⅰ)中所选择的模型,求出关于的回归方程(计算过程中四舍五入保留两位小数),并求温度为时,产卵数的预报值.
参考数据:,,.
22.开普勒说:“我珍视类比胜过任何别的东西,它是我最可信赖的老师,它能揭示自然界的秘密,”波利亚也曾说过:“类比是一个伟大的引路人,求解立体几何问题往往有赖于平面几何中的类比问题.”在选修1—2第二章《推理与证明》的学习中,我们知道,平面图形很多可以推广到空间中去,例如正三角形可以推广到正四面体,圆可以推广到球,平行四边形可以推广到平行六面体等.
如图,如果四面体中棱,,两两垂直,那么称四面体为直角四面体.请类比直角三角形(表示斜边上的高)中的性质给出直角四面体中的两个性质,并给出证明.
直角三角形
直角四面体
条件
,,
结论1
结论2
郑州市2020—2021下期高二文科数学考试评分参考
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题
13.;
14.;
15.(,)备注:考生不写小括号内容不给分.
16.(或者).
三、解答题
17.解:(1)由题意知,,,,
所以,
同理,
由,得,
则点对应的复数.
(2)由,得,即.
四边形为矩形
、、、四点共圆.
18.解:(1)因为曲线的极坐标方程为.
将,,代入上式,得.
所以曲线的直角坐标方程为;
又曲线为椭圆,其左顶点坐标为,
直线的参数方程为:(为参数).
(2)设椭圆的内接矩形在第一象限的顶点为,
椭圆的内接矩形的周长为:
(其中,)
椭圆的内接矩形的周长的最大值为.
(选修4—5:不等式选讲)
解:(1)依题意,
所以,当时,;
函数的图象如图所示:
(2)由(1)可知,利用图象法,直线只与的图像相交于,
由解得
故当时,直线在图象的上方,
即,故解集为.
19.解:(1)根据所给等高条形图数据,完成列联表如下:
晚上
白天
合计
男婴
女婴
合计
根据等高条形图,在男婴样本中白天出生的频率要高于女婴样本中白天出生的频率;
根据列联表,男婴样本中白天出生的频率为,女婴样本中白天出生的频率为.
因此可以直观得到结论:婴儿的性别和出生时间有关系(二者选其一即可给分)
(2)根据(1)中列联表,计算,
所以能在犯错误概率不超过的前提下认为婴儿的性别和出生的时间有关.
20.(选修4-4:坐标系与参数方程)
解:(1)依题意,因为射线:,故射线:;
因为的参数方程为:,可得曲线的普通方程:.
(2)曲线的方程为,故曲线的极坐标方程为.
设点、对应的极坐标分别为,,
联立与,得解得
联立与,得解得
故
(选修4—5:不等式选讲)
解:(1)当时,原不等式可化为等价于
或或
即或,所以不等式的解集是.
(2)若存在这样的,使得的解集中包含.
即当时,恒成立.
可得,得,得.
所以解得
所以存在这样的,满足使得的解集中包含.
21.解:(1)应该选择模型①.
理由为:模型①残差点比较均匀地落在水平的带状区域中,且带状区域的宽度比模型②带状宽度窄,所以模型①的拟合精度更高,回归方程的预报精度相应就会越高.故选模型①比较合适.
(2)由(1)知,选用模型①,,用两边取对数,得,
令,与温度可以用线性回归方程来拟合,
则,
,
,
于是有,
所以产卵数关于温度的回归方程为.
当时,(个),
所以,在气温在时,一个红铃虫的产卵数的预报值为个.
22.解:记、、、的面积依次为、、、,
记,,.
结论1:,
证明:过作,垂足为,连接,
在中,
DH=,
,
,
.
结论2:
证明:过作,垂足为,连接,
过作,垂足为,设,
,
.
.
高二数学(文)试题
注意事项:
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.考试时间120分钟,满分150分.考生应首先阅读答题卡上的文字信息,然后在答题卡上作答,在试题卷上作答无效.交卷时只交答题卡.
参考公式和数据:
1.对于一组具有线性相关关系的数据,其回归直线的斜率和截距的最小二乘估计分别为:,;
2.,;
3.参考数据:
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.在用反证法证明命题“已知,,且.求证:,中至少有一个小于4”时,假设正确的是(
)
A.假设,都不大于
B.假设,都不小于
C.假设,都小于
D.假设,都大于
2.如图,复平面内的点对应的复数记为,则对应的点位于(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.中国茶文化博大精深,茶水的口感与茶叶的类型和水的温度有关某数学建模小组建立了茶水冷却时间和茶水温度的一组数据.经过分析,提出了四种回归模型,①②③④四种模型的残差平方和的值分别是,,,.则拟合效果最好的模型是(
)
A.模型①
B.模型②
C.模型③
D.模型④
4.(选修4-4:坐标系与参数方程)将曲线变换为曲线的一个伸缩变换为(
)
A.
B.
C.
D.
(选修4-5:不等式选讲)若关于的不等式的解集为空集,则实数的取值范围是(
)
A.
B.
C.
D.
5.已知糖水中含有糖,若再添加糖完全溶解在其中,则糖水变得更甜了(即糖水中含糖浓度变大).根据这个事实,下列不等式中一定成立的是(
)
A.
B.
C.
D.
6.“关注夕阳,爱老敬老”,某商会从2016年开始向晚晴山庄养老院捐赠物资和现金.下表记录了第年(2016年为第一年)捐赠现金(万元)的数据情况.由表中数据得到了关于的线性回归方程为,预测2021年该商会捐赠现金______万元.
A.
B.
C.
D.
7.若输出的的值等于,那么在程序框图中的判断框内应填写的条件是(
)
A.
B.
C.
D.
8.已知正数,满足,则的最小值为(
)
A.
B.
C.
D.
9.任何一个复数都可以表示成的形式,我们把叫做复数的三角形式.已知,则下列结论正确的是(
)
A.的实部为
B.
C.
D.
10.(选修4-4:坐标系与参数方程)已知曲线的参数方程(为参数,且).若以下曲线中有一个是,则曲线是(
)
A.
B.
C.
D.
(选修4-5:不等式选讲)已知,若恒成立,则的最大值为(
)
A.
B.
C.
D.
11.胡夫金字塔的形状为正四棱锥.1859年,英国作家约翰·泰勒在其《大金字塔》一书中提出:埃及人在建造胡夫金字塔时利用了黄金比例,泰勒还引用了古希腊历史学家希罗多德的记载:胡夫金字塔的每一个侧面的面积都等于金字塔高的平方,如图,即.已知四棱锥底面是边长约为英尺的正方形,顶点的投影在底面中心,为中点,根据以上条件,的长度(单位:英尺)约为(
)
A.
B.
C.
D.
12.已知,若,则与的大小关系为(
)
A.
B.
C.
D.不确定
第Ⅱ卷(非选择题,共90分)
二、填空题:本题共4小题,每小题5分,共20分.
13.若为方程(,)的一个根,则______.
14.从某大学随机选择名女大学生,其身高和体重数据如表所示:
身高()
体重()
根据表中的数据可得回归直线方程,,这表明女大学生的体重差异有______是由身高引起的.
15.在等差数列中,若,则(,).类比上述性质,在等比数列中,若,则存在的等式为______.
16.已知函数有五个不同的零点,且所有零点之和为,则实数的值为______.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.为复平面内的平行四边形,向量对应的复数为,对应的复数为,对应的复数为.
(Ⅰ)求点对应的复数;
(Ⅱ)判断、、、四点是否在同一个圆上?并证明你的结论.
18.(选修4-4:坐标系与参数方程)在平面直角坐标系中,以坐标原点为极点,轴的非负半轴为极轴且取相同的单位长度建立板坐标系,已知曲线的极坐标方程为;直线的倾斜角为,且经过曲线的左顶点.
(Ⅰ)求曲线的直角坐标方程和直线的参数方程;
(Ⅱ)求曲线的内接矩形的周长的最大值.
(选修4-5:不等式选讲)已知函数.
(Ⅰ)求的最大值,并在网格纸中作出函数的图象;
(Ⅱ)求的解集.
19.调查某医院某段时间内婴儿出生的时间与性别的关系,随机调查了一段时间内该医院名男宝宝和名女宝宝的出生时间,通过分析数据得到下面等高条形图:
(Ⅰ)根据所给等高条形图数据,完成下面的列联表,并通过图形和数据直观判断婴儿性别与出生时间是否有关?
晚上
白天
合计
男婴
女婴
合计
(Ⅱ)根据(Ⅰ)中列联表,能否在犯错误概率不超过的前提下认为婴儿的性别与出生的时间有关?
20.(选修4-4:坐标系与参数方程)平面直角坐标系中,射线:,曲线的参数方程为(为参数);以原点为极点,轴的非负半轴为极轴建立极坐标系,曲线的极坐标方程为.
(Ⅰ)写出射线的极坐标方程、曲线的普通方程;
(Ⅱ)已知射线与交于点,与交于点(异于点),求的值.
(选修4-5:不等式选讲)已知函数.
(Ⅰ)当时,求不等式的解集;
(Ⅱ)是否存在实数使得的解集中包含.若存在,求的取值范围;若不存在,说明理由.
21.红铃虫是棉花的主要害虫之一,其产卵数与温度有关.现收集到一只红铃虫的产卵数(个)和温度()的组观测数据,制成图1所示的散点图现用两种模型①(,),②分别进行拟合,由此得到相应的回归方程并进行残差分析,进一步得到图2所示的残差图.
根据收集到的数据,计算得到如下值:
表中;;;.
(Ⅰ)根据残差图,比较模型①、②的拟合效果,应选择哪个模型?并说明理由;
(Ⅱ)根据(Ⅰ)中所选择的模型,求出关于的回归方程(计算过程中四舍五入保留两位小数),并求温度为时,产卵数的预报值.
参考数据:,,.
22.开普勒说:“我珍视类比胜过任何别的东西,它是我最可信赖的老师,它能揭示自然界的秘密,”波利亚也曾说过:“类比是一个伟大的引路人,求解立体几何问题往往有赖于平面几何中的类比问题.”在选修1—2第二章《推理与证明》的学习中,我们知道,平面图形很多可以推广到空间中去,例如正三角形可以推广到正四面体,圆可以推广到球,平行四边形可以推广到平行六面体等.
如图,如果四面体中棱,,两两垂直,那么称四面体为直角四面体.请类比直角三角形(表示斜边上的高)中的性质给出直角四面体中的两个性质,并给出证明.
直角三角形
直角四面体
条件
,,
结论1
结论2
郑州市2020—2021下期高二文科数学考试评分参考
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题
13.;
14.;
15.(,)备注:考生不写小括号内容不给分.
16.(或者).
三、解答题
17.解:(1)由题意知,,,,
所以,
同理,
由,得,
则点对应的复数.
(2)由,得,即.
四边形为矩形
、、、四点共圆.
18.解:(1)因为曲线的极坐标方程为.
将,,代入上式,得.
所以曲线的直角坐标方程为;
又曲线为椭圆,其左顶点坐标为,
直线的参数方程为:(为参数).
(2)设椭圆的内接矩形在第一象限的顶点为,
椭圆的内接矩形的周长为:
(其中,)
椭圆的内接矩形的周长的最大值为.
(选修4—5:不等式选讲)
解:(1)依题意,
所以,当时,;
函数的图象如图所示:
(2)由(1)可知,利用图象法,直线只与的图像相交于,
由解得
故当时,直线在图象的上方,
即,故解集为.
19.解:(1)根据所给等高条形图数据,完成列联表如下:
晚上
白天
合计
男婴
女婴
合计
根据等高条形图,在男婴样本中白天出生的频率要高于女婴样本中白天出生的频率;
根据列联表,男婴样本中白天出生的频率为,女婴样本中白天出生的频率为.
因此可以直观得到结论:婴儿的性别和出生时间有关系(二者选其一即可给分)
(2)根据(1)中列联表,计算,
所以能在犯错误概率不超过的前提下认为婴儿的性别和出生的时间有关.
20.(选修4-4:坐标系与参数方程)
解:(1)依题意,因为射线:,故射线:;
因为的参数方程为:,可得曲线的普通方程:.
(2)曲线的方程为,故曲线的极坐标方程为.
设点、对应的极坐标分别为,,
联立与,得解得
联立与,得解得
故
(选修4—5:不等式选讲)
解:(1)当时,原不等式可化为等价于
或或
即或,所以不等式的解集是.
(2)若存在这样的,使得的解集中包含.
即当时,恒成立.
可得,得,得.
所以解得
所以存在这样的,满足使得的解集中包含.
21.解:(1)应该选择模型①.
理由为:模型①残差点比较均匀地落在水平的带状区域中,且带状区域的宽度比模型②带状宽度窄,所以模型①的拟合精度更高,回归方程的预报精度相应就会越高.故选模型①比较合适.
(2)由(1)知,选用模型①,,用两边取对数,得,
令,与温度可以用线性回归方程来拟合,
则,
,
,
于是有,
所以产卵数关于温度的回归方程为.
当时,(个),
所以,在气温在时,一个红铃虫的产卵数的预报值为个.
22.解:记、、、的面积依次为、、、,
记,,.
结论1:,
证明:过作,垂足为,连接,
在中,
DH=,
,
,
.
结论2:
证明:过作,垂足为,连接,
过作,垂足为,设,
,
.
.
