2020-2021学年人教版七年级下册第五章 相交线与平行线小结与复习(22张PPT)
文档属性
| 名称 | 2020-2021学年人教版七年级下册第五章 相交线与平行线小结与复习(22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 658.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-22 15:00:33 | ||
图片预览



文档简介
(共22张PPT)
小结与复习
第五章
相交线与平行线
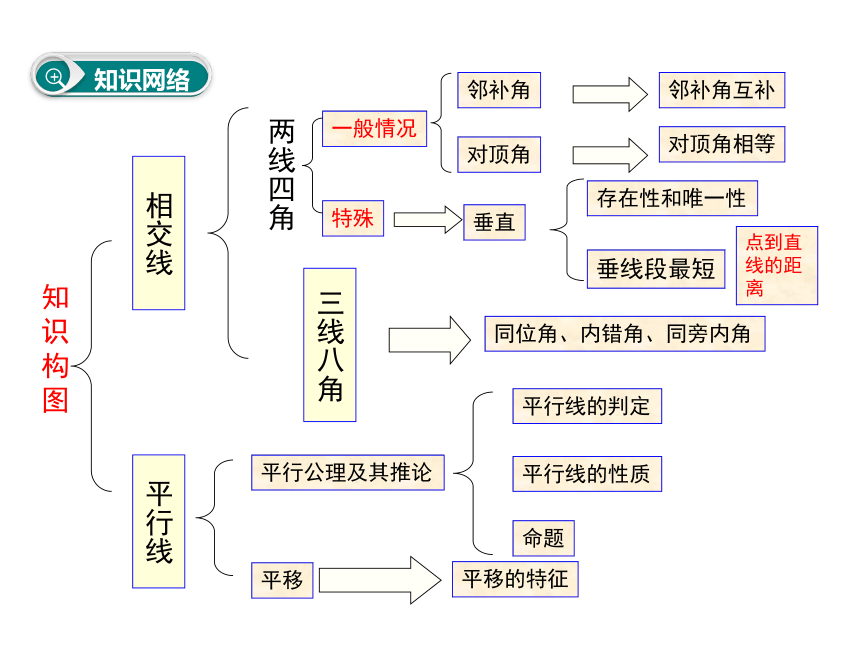
知识网络
相交线
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
特殊
垂直
存在性和唯一性
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
平行线
平行公理及其推论
平行线的判定
平行线的性质
平移
平移的特征
命题
知识构图
两线四角
三线八角
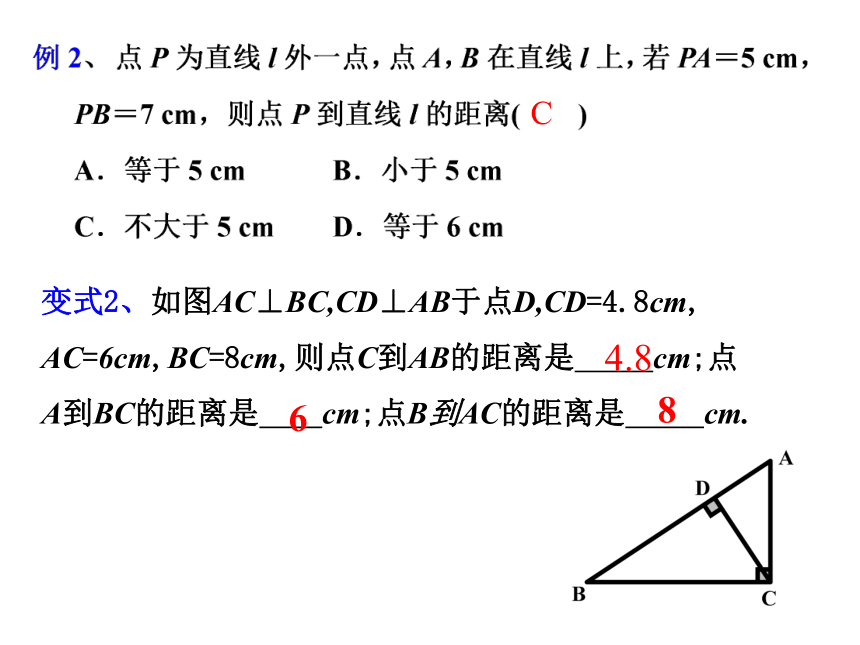
C
变式2、如图AC⊥BC,CD⊥AB于点D,CD=4.8cm,
AC=6cm,BC=8cm,则点C到AB的距离是
cm;点A到BC的距离是
cm;点B到AC的距离是
cm.
4.8
6
8
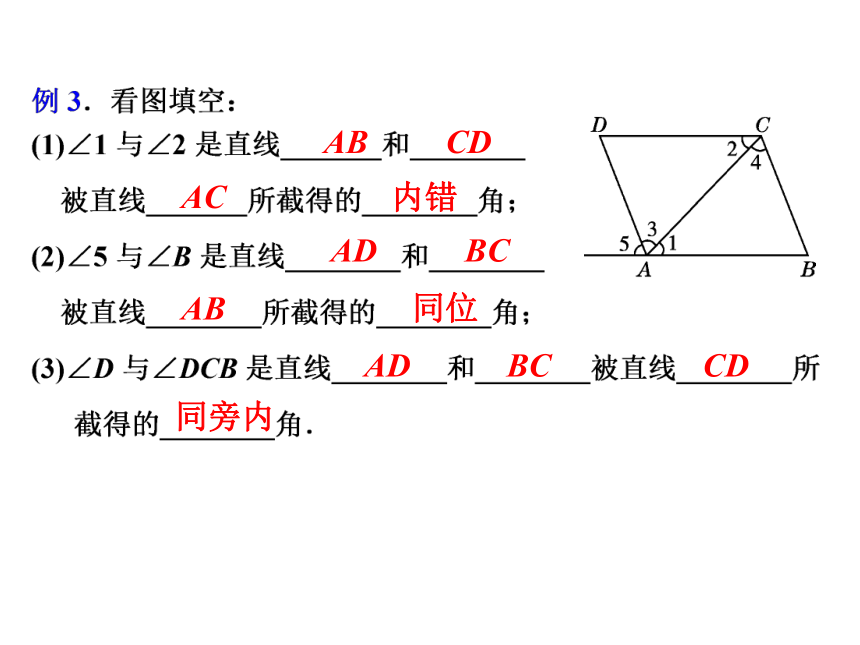
AB
CD
AC
内错
AD
BC
AB
同位
AD
BC
CD
同旁内
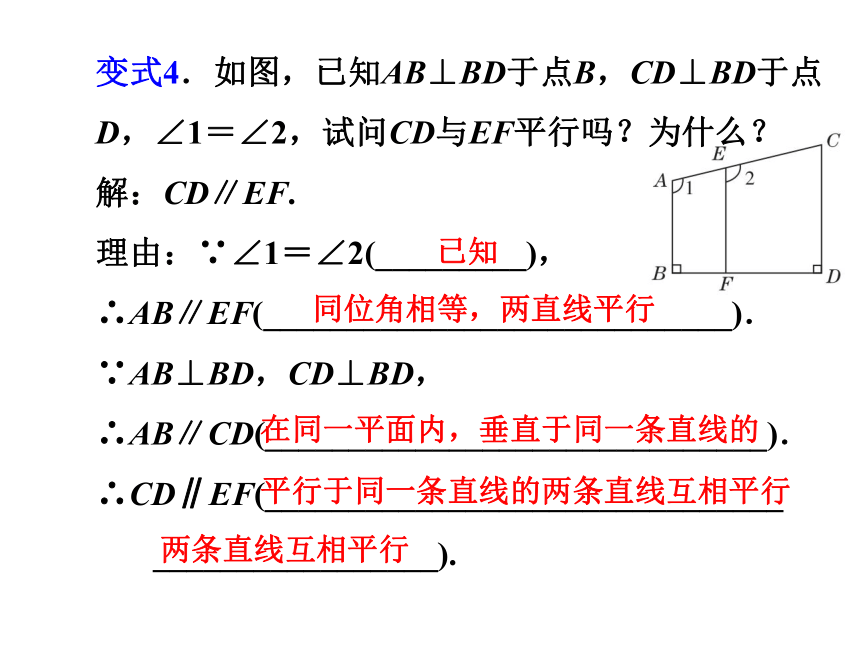
变式4.如图,已知AB⊥BD于点B,CD⊥BD于点D,∠1=∠2,试问CD与EF平行吗?为什么?
解:CD∥EF.
理由:∵∠1=∠2(_________),
∴AB∥EF(____________________________).
∵AB⊥BD,CD⊥BD,
∴AB∥CD(______________________________).
∴CD∥EF(_______________________________
_________________).
已知
同位角相等,两直线平行
在同一平面内,垂直于同一条直线的
平行于同一条直线的两条直线互相平行
两条直线互相平行
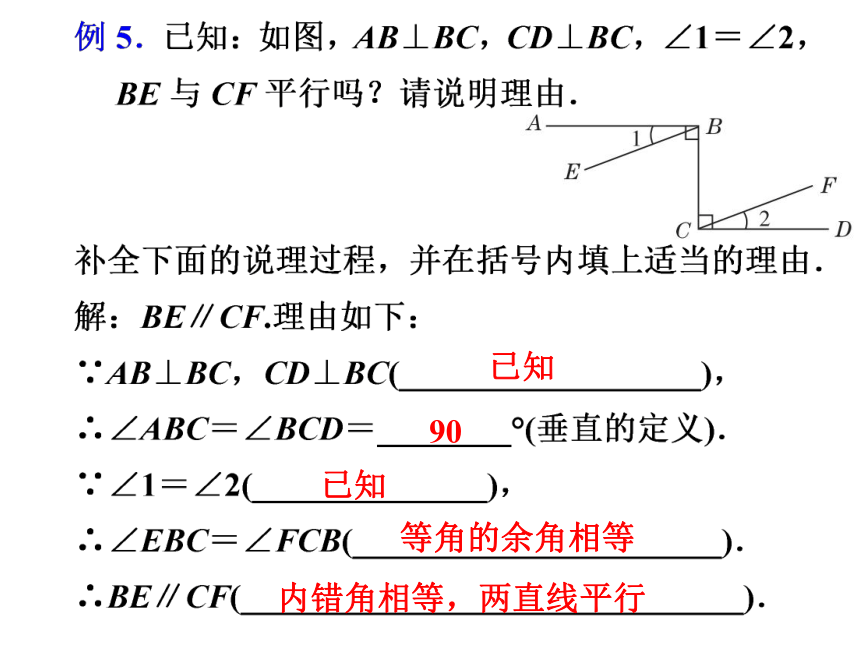
已知
90
已知
等角的余角相等
内错角相等,两直线平行
解:DE∥AB,EF∥BC.
理由:设∠1=2x0,则∠2=3x0,∠3=4x0
∵∠1+∠2+∠3=180°,
∴2x°+3x°+4x°=180°,解得x°=20°.
∴∠2=60°.∵∠AFE=60°,∴∠AFE=∠2=60°.
∴DE∥AB.∵∠BDE=120°,
∴∠BDE+∠2=120°+60°=180°.∴EF∥BC.
C
B
变式7(1).如图1,已知
AB∥CD,
∠1=30°,
∠2=90°,则∠3=
°
(2).如图2,若AE∥CD,∠EBF=135°,∠BFD=60°,
∠D=(
)
A.75°
B.45°
C.30°
D.15°
图1
图2
60
D
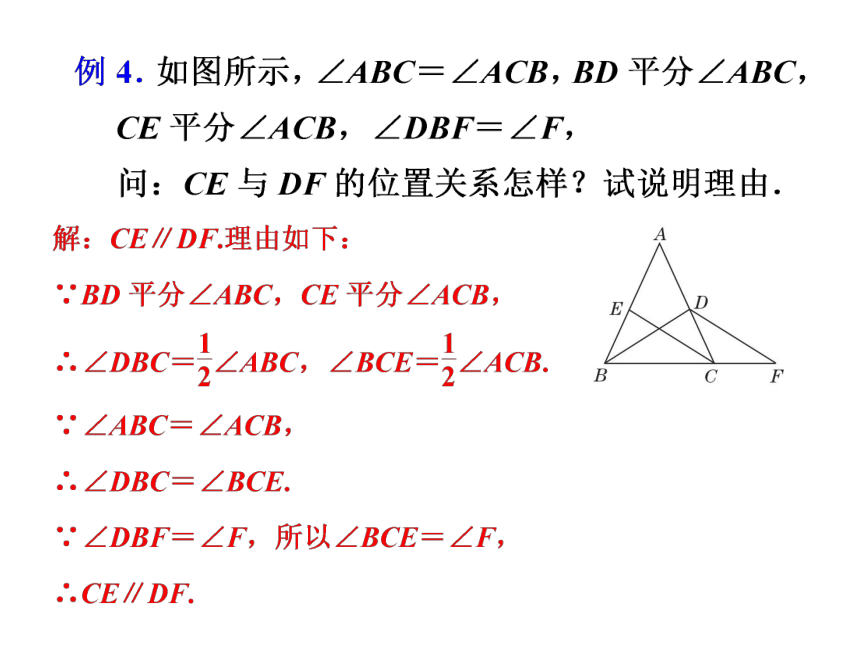
变式8、如图,点A,B,C,D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF.
求证:∠E=∠F.
例8、已知命题“如果两条射线是两条平行线被第三条直线所截得到的一对内错角的平分线,那么这两条射线互相平行”.
(1)写出命题的题设和结论;
解:题设:两条射线是两条平行线被第三条直线所截得到的一对内错角的平分线;结论:这两条射线互相平行.
(2)画出图形,并用数学符号叙述这个命题;
解:如图,如果AB∥CD,直线AB,CD被直线EF所截,EG平分∠AEF,FH平分∠EFD,那么EG∥FH.
例9、如图所示,下列四组图形中,有一组中的两个图形经过平移其中一个能得到另一个,这组图形是
(
)
D
变式10、如图所示,△DEF经过平移得到△ABC,
那么∠C的对应角和ED的对应边分别是
(
)
A.∠F,AC
B.∠BOD,BA
C.∠F,BA
D.∠BOD,AC
C
小结与复习
第五章
相交线与平行线
知识网络
相交线
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
特殊
垂直
存在性和唯一性
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
平行线
平行公理及其推论
平行线的判定
平行线的性质
平移
平移的特征
命题
知识构图
两线四角
三线八角
C
变式2、如图AC⊥BC,CD⊥AB于点D,CD=4.8cm,
AC=6cm,BC=8cm,则点C到AB的距离是
cm;点A到BC的距离是
cm;点B到AC的距离是
cm.
4.8
6
8
AB
CD
AC
内错
AD
BC
AB
同位
AD
BC
CD
同旁内
变式4.如图,已知AB⊥BD于点B,CD⊥BD于点D,∠1=∠2,试问CD与EF平行吗?为什么?
解:CD∥EF.
理由:∵∠1=∠2(_________),
∴AB∥EF(____________________________).
∵AB⊥BD,CD⊥BD,
∴AB∥CD(______________________________).
∴CD∥EF(_______________________________
_________________).
已知
同位角相等,两直线平行
在同一平面内,垂直于同一条直线的
平行于同一条直线的两条直线互相平行
两条直线互相平行
已知
90
已知
等角的余角相等
内错角相等,两直线平行
解:DE∥AB,EF∥BC.
理由:设∠1=2x0,则∠2=3x0,∠3=4x0
∵∠1+∠2+∠3=180°,
∴2x°+3x°+4x°=180°,解得x°=20°.
∴∠2=60°.∵∠AFE=60°,∴∠AFE=∠2=60°.
∴DE∥AB.∵∠BDE=120°,
∴∠BDE+∠2=120°+60°=180°.∴EF∥BC.
C
B
变式7(1).如图1,已知
AB∥CD,
∠1=30°,
∠2=90°,则∠3=
°
(2).如图2,若AE∥CD,∠EBF=135°,∠BFD=60°,
∠D=(
)
A.75°
B.45°
C.30°
D.15°
图1
图2
60
D
变式8、如图,点A,B,C,D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF.
求证:∠E=∠F.
例8、已知命题“如果两条射线是两条平行线被第三条直线所截得到的一对内错角的平分线,那么这两条射线互相平行”.
(1)写出命题的题设和结论;
解:题设:两条射线是两条平行线被第三条直线所截得到的一对内错角的平分线;结论:这两条射线互相平行.
(2)画出图形,并用数学符号叙述这个命题;
解:如图,如果AB∥CD,直线AB,CD被直线EF所截,EG平分∠AEF,FH平分∠EFD,那么EG∥FH.
例9、如图所示,下列四组图形中,有一组中的两个图形经过平移其中一个能得到另一个,这组图形是
(
)
D
变式10、如图所示,△DEF经过平移得到△ABC,
那么∠C的对应角和ED的对应边分别是
(
)
A.∠F,AC
B.∠BOD,BA
C.∠F,BA
D.∠BOD,AC
C
