2020-2021学年人教版七年级下册第七章 平面直角坐标系小结与复习课件(14张PPT)
文档属性
| 名称 | 2020-2021学年人教版七年级下册第七章 平面直角坐标系小结与复习课件(14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 324.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-22 15:03:54 | ||
图片预览






文档简介
(共14张PPT)
小结与复习
第七章
平面直角坐标系
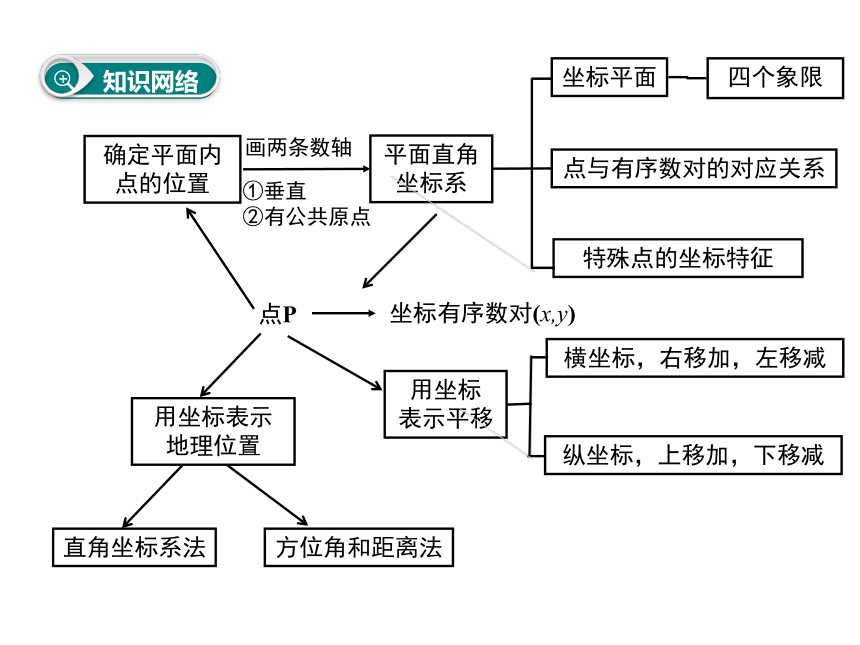
知识网络
确定平面内点的位置
平面直角
坐标系
坐标平面
四个象限
点与有序数对的对应关系
特殊点的坐标特征
点P
画两条数轴
①垂直
②有公共原点
坐标有序数对(x,y)
用坐标
表示平移
横坐标,右移加,左移减
纵坐标,上移加,下移减
用坐标表示
地理位置
直角坐标系法
方位角和距离法
例1.下列说法错误的是( )
A.平面内两条互相垂直的数轴就构成了平面直角坐标系
B.平面直角坐标系中两条数轴是互相垂直的
C.坐标平面被两条坐标轴分成了四个部分,每个部分称为象限
D.坐标轴上的点不属于任何象限
A
A
A
变式1、已知点A(-3+a,2a+9)在第二象限,且到x轴的
距离为5,则点a的值是
.
-2
C
变式3.(1)点A(2,3)到x轴的距离为
;点B(-4,0)到y
轴的距离为
;点C到x轴的距离为1,到y轴的
距离为3,且在第三象限,则C点坐标是 .
3个单位
4个单位
(-3
,-1)
(2)
4.直角坐标系中,在y轴上有一点P
,且OP=5,则P的坐标为
.
(0
,5)或(0
,-5)
变式4
(1)已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则
m的值为______
-1
(2)已知:A(1,2),B(x,y),AB∥x轴,且B到y轴距离为2,则
点B的坐标是
.
(2,2)或(-2,2)
例4、在平面直角坐标系中,将点P(3,2)向下平移2个单位长度得到的点的坐标是( )
A.(3,0)
B.(1,2)
C.(5,2)
D.(3,4)
A
A
例5、如图,把?ABC经过一定的变换得到?A′B′C′,如果三角形ABC上点P的坐标为(a,b),那么点P变换后的对应点P′的坐标为
.
(a+3,b+2)
A(-3,-2)
A′(0,0)
横坐标加3
纵坐标加2
变式6、将点P(-3,y)向下平移3个单位,再向左平移2个单位得到点Q(x,-1),则xy=
.
-10
4
2
1
变式7、如图,已知四边形ABCD.
(1)写出点A,B,C,D的坐标;
(2)试求四边形ABCD的面积.
解:A(-2,1),B(-3,-2),
C(3,-2),D(1,2).
变式8、已知直角三角形ABC的直角边BC=AC,且B(3,2),C(3,-2),求点A的坐标及三角形ABC的面积.
A
B
C
O
x
y
解:∵B(3,2),C(3,-2),
∴BC∥y轴,且BC=2-(-2)=4,
∴AC=BC=4.
∴三角形ABC面积是1/2×4×4=8.
∵AC⊥BC,∴AC⊥y轴,
∴点A的横坐标为3-4=-1,纵坐标为-2,
∴A点坐标为(-1,-2).
课堂小结
平面直角坐标系
概念及
有关知识
坐标方法
的应用
有序数对(a,b)
坐标系画法(坐标、x轴和y轴、象限)
平面上的点
点的坐标
表示地理位置(选、建、标、写)
表示平移
小结与复习
第七章
平面直角坐标系
知识网络
确定平面内点的位置
平面直角
坐标系
坐标平面
四个象限
点与有序数对的对应关系
特殊点的坐标特征
点P
画两条数轴
①垂直
②有公共原点
坐标有序数对(x,y)
用坐标
表示平移
横坐标,右移加,左移减
纵坐标,上移加,下移减
用坐标表示
地理位置
直角坐标系法
方位角和距离法
例1.下列说法错误的是( )
A.平面内两条互相垂直的数轴就构成了平面直角坐标系
B.平面直角坐标系中两条数轴是互相垂直的
C.坐标平面被两条坐标轴分成了四个部分,每个部分称为象限
D.坐标轴上的点不属于任何象限
A
A
A
变式1、已知点A(-3+a,2a+9)在第二象限,且到x轴的
距离为5,则点a的值是
.
-2
C
变式3.(1)点A(2,3)到x轴的距离为
;点B(-4,0)到y
轴的距离为
;点C到x轴的距离为1,到y轴的
距离为3,且在第三象限,则C点坐标是 .
3个单位
4个单位
(-3
,-1)
(2)
4.直角坐标系中,在y轴上有一点P
,且OP=5,则P的坐标为
.
(0
,5)或(0
,-5)
变式4
(1)已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则
m的值为______
-1
(2)已知:A(1,2),B(x,y),AB∥x轴,且B到y轴距离为2,则
点B的坐标是
.
(2,2)或(-2,2)
例4、在平面直角坐标系中,将点P(3,2)向下平移2个单位长度得到的点的坐标是( )
A.(3,0)
B.(1,2)
C.(5,2)
D.(3,4)
A
A
例5、如图,把?ABC经过一定的变换得到?A′B′C′,如果三角形ABC上点P的坐标为(a,b),那么点P变换后的对应点P′的坐标为
.
(a+3,b+2)
A(-3,-2)
A′(0,0)
横坐标加3
纵坐标加2
变式6、将点P(-3,y)向下平移3个单位,再向左平移2个单位得到点Q(x,-1),则xy=
.
-10
4
2
1
变式7、如图,已知四边形ABCD.
(1)写出点A,B,C,D的坐标;
(2)试求四边形ABCD的面积.
解:A(-2,1),B(-3,-2),
C(3,-2),D(1,2).
变式8、已知直角三角形ABC的直角边BC=AC,且B(3,2),C(3,-2),求点A的坐标及三角形ABC的面积.
A
B
C
O
x
y
解:∵B(3,2),C(3,-2),
∴BC∥y轴,且BC=2-(-2)=4,
∴AC=BC=4.
∴三角形ABC面积是1/2×4×4=8.
∵AC⊥BC,∴AC⊥y轴,
∴点A的横坐标为3-4=-1,纵坐标为-2,
∴A点坐标为(-1,-2).
课堂小结
平面直角坐标系
概念及
有关知识
坐标方法
的应用
有序数对(a,b)
坐标系画法(坐标、x轴和y轴、象限)
平面上的点
点的坐标
表示地理位置(选、建、标、写)
表示平移
