2020-2021学年人教版七年级下册第九章 不等式与不等式组小结与复习课件(23张PPT)
文档属性
| 名称 | 2020-2021学年人教版七年级下册第九章 不等式与不等式组小结与复习课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 449.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-22 15:07:24 | ||
图片预览








文档简介
(共23张PPT)
小结与复习
第九章
不等式与不等式组
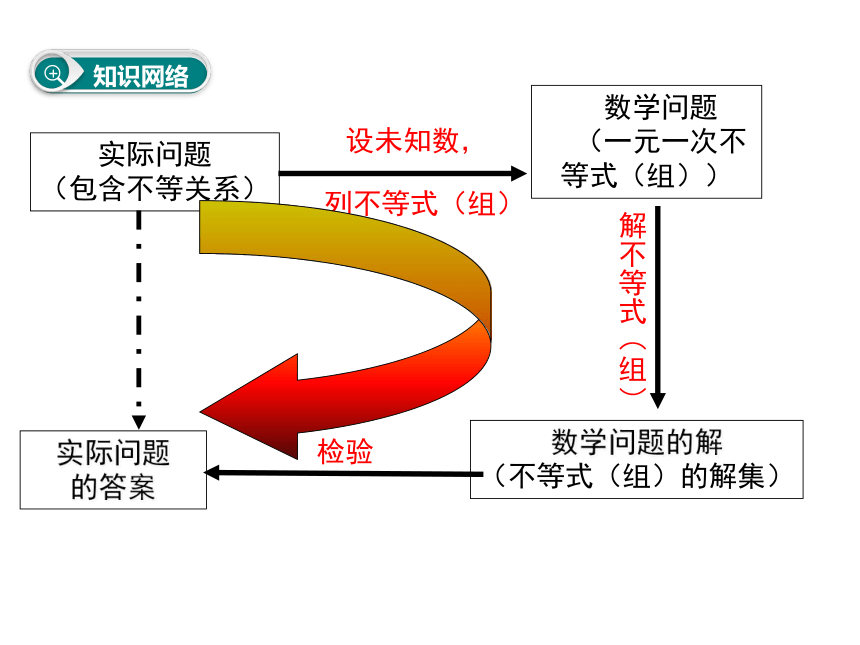
数学问题的解
(不等式(组)的解集)
知识网络
实际问题
(包含不等关系)
设未知数,
列不等式(组)
数学问题
(一元一次不等式(组))
解不等式(组)
检验
实际问题
的答案
例1.判断下列各式哪些是等式?哪些是不等式?哪些既不是等式也不是不等式?
(1)x+y;
(2)3x>7;
(3)5=2x+3;
(4)x2>0;
(5)2x-3y=1;
(6)52;
(7)2<3.
解:等式有(3)(5),不等式有(2)(4)(7),既不是等式也不是不等式的有(1)(6).
B
变式1、下列式子中,一元一次不等式有(
)
①3x-1≥4
②
2+3x>6
③
3-
<5
④
⑤
⑥
x+xy≥y2
⑦x>0
A.5个
B.4个
C.6个
D.3个
A
√
√
×
√
√
×
√
例3、下列说法中正确的是( )
A.x=1是方程-2x=2的解
B.x=-1是不等式-2x>2的唯一解
C.x=-2是不等式-2x>2的解集
D.x=-2,-3都是不等式-2x>2的解且它的解有无数个
D
B
C
C
D
解:(1)去分母,得x+1≥6(x-1)-8,
去括号,得x+1≥6x-6-8,
移项,得x-6x≥-6-8-1,
合并同类项,得-5x≥-15.
系数化为1,得x≤3.
解:(2)去分母,得4x-2>3x-1,
移项,得4x-3x>2-1,
合并同类项,得x>1,
将不等式的解集表示在数轴上如图所示.
变式5、解不等式,并把它们的解集在数轴上表示出来.
(1)3[x-2(x-2)]>x-3(x-2);
(2)
解:
(1)x<6,数轴上表示为
0
6
(2)y<2,数轴上表示为
0
2
变式6、解不等式组:
①
②
解:①不等式组的解集是
;
②不等式组的解集是x≥9.
例8、已知不等式组
有解,则a的取值范围为
(
)
A.a>-2
B.a≥-2
C.a<2
D.a≥2
C
例9、小明上午8时20分出发去郊游,10时20分时,小亮乘车从同一地点出发,已知小明每小时走4千米,那么小亮要在11时追上或超过小明,速度至少应是多少?
解:设小亮的速度为x千米/时,40分=
小时,
列不等式,得
,解得x≥16.
答:小亮的速度至少为16千米/时.
例10、一堆玩具分给若干个小朋友,若每人分3件,则剩余4件;若前面每人分4件,则最后一人得到的玩具不足3件,求小朋友的人数与玩具数.
解:
设小朋友总共有x人,由此可得不等式组
3x+4-4(x-1)≥0,
3x+4-4(x-1)<3;
由此可得5所以x=6,7,8.
答:小朋友有6人,玩具有22件;或小朋友有7人,玩具有25件;或小朋友有8人,玩具有28件.
课堂小结
1.一元一次不等式的定义和性质
2.一元一次不等式的解法及应用
3.一元一次不等式组的定义、解集及应用
小结与复习
第九章
不等式与不等式组
数学问题的解
(不等式(组)的解集)
知识网络
实际问题
(包含不等关系)
设未知数,
列不等式(组)
数学问题
(一元一次不等式(组))
解不等式(组)
检验
实际问题
的答案
例1.判断下列各式哪些是等式?哪些是不等式?哪些既不是等式也不是不等式?
(1)x+y;
(2)3x>7;
(3)5=2x+3;
(4)x2>0;
(5)2x-3y=1;
(6)52;
(7)2<3.
解:等式有(3)(5),不等式有(2)(4)(7),既不是等式也不是不等式的有(1)(6).
B
变式1、下列式子中,一元一次不等式有(
)
①3x-1≥4
②
2+3x>6
③
3-
<5
④
⑤
⑥
x+xy≥y2
⑦x>0
A.5个
B.4个
C.6个
D.3个
A
√
√
×
√
√
×
√
例3、下列说法中正确的是( )
A.x=1是方程-2x=2的解
B.x=-1是不等式-2x>2的唯一解
C.x=-2是不等式-2x>2的解集
D.x=-2,-3都是不等式-2x>2的解且它的解有无数个
D
B
C
C
D
解:(1)去分母,得x+1≥6(x-1)-8,
去括号,得x+1≥6x-6-8,
移项,得x-6x≥-6-8-1,
合并同类项,得-5x≥-15.
系数化为1,得x≤3.
解:(2)去分母,得4x-2>3x-1,
移项,得4x-3x>2-1,
合并同类项,得x>1,
将不等式的解集表示在数轴上如图所示.
变式5、解不等式,并把它们的解集在数轴上表示出来.
(1)3[x-2(x-2)]>x-3(x-2);
(2)
解:
(1)x<6,数轴上表示为
0
6
(2)y<2,数轴上表示为
0
2
变式6、解不等式组:
①
②
解:①不等式组的解集是
;
②不等式组的解集是x≥9.
例8、已知不等式组
有解,则a的取值范围为
(
)
A.a>-2
B.a≥-2
C.a<2
D.a≥2
C
例9、小明上午8时20分出发去郊游,10时20分时,小亮乘车从同一地点出发,已知小明每小时走4千米,那么小亮要在11时追上或超过小明,速度至少应是多少?
解:设小亮的速度为x千米/时,40分=
小时,
列不等式,得
,解得x≥16.
答:小亮的速度至少为16千米/时.
例10、一堆玩具分给若干个小朋友,若每人分3件,则剩余4件;若前面每人分4件,则最后一人得到的玩具不足3件,求小朋友的人数与玩具数.
解:
设小朋友总共有x人,由此可得不等式组
3x+4-4(x-1)≥0,
3x+4-4(x-1)<3;
由此可得5
答:小朋友有6人,玩具有22件;或小朋友有7人,玩具有25件;或小朋友有8人,玩具有28件.
课堂小结
1.一元一次不等式的定义和性质
2.一元一次不等式的解法及应用
3.一元一次不等式组的定义、解集及应用
