2020-2021学年人教版八年级下册第十七章勾股定理章末小结课件(22张PPT)
文档属性
| 名称 | 2020-2021学年人教版八年级下册第十七章勾股定理章末小结课件(22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 437.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-22 15:11:16 | ||
图片预览





文档简介
(共22张PPT)
第十七章
勾股定理
章末小结
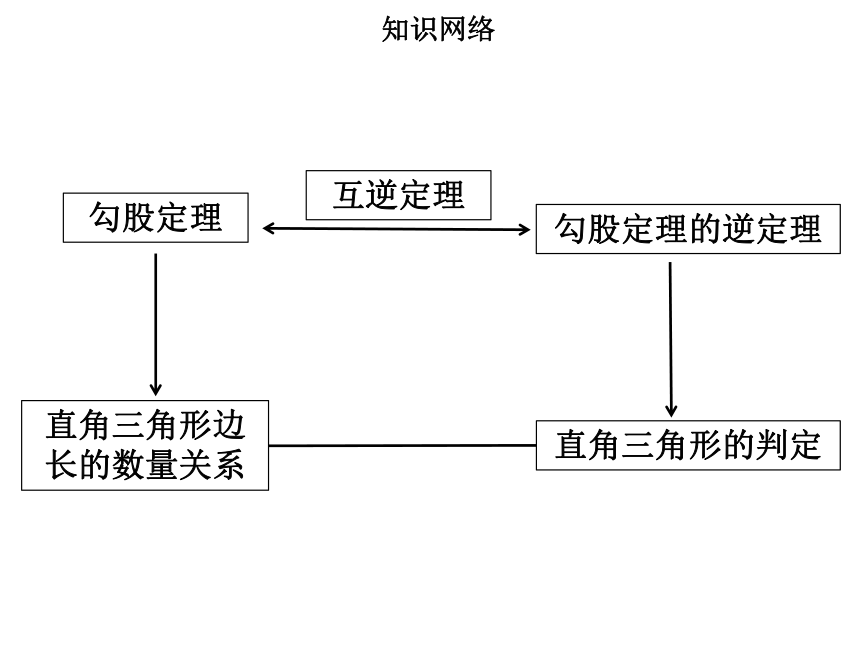
知识网络
勾股定理
勾股定理的逆定理
互逆定理
直角三角形边长的数量关系
直角三角形的判定
例1.有下列命题:①直角都相等;
②内错角相等,两直线平行;
③如果a+b>0,那么a>0,b>0;
④相等的角都是直角;
⑤如果a>0,b>0,那么ab>0;
⑥两直线平行,内错角相等.
(1)③和⑤是互逆命题吗?
(2)你能说出③和⑤的逆命题各是什么吗?
(3)请指出哪几个命题是互逆命题.
解:(1)由于③的题设是a+b>0,而⑤的结论是ab>0,故⑤不是由③交换命题的题设和结论得到的,所以③和⑤不是互逆命题.
(2)能.③的逆命题是:如果a>0,b>0,那么a+b>0;⑤的逆命题是:如果ab>0,那么a>0,b>0.
(3)①与④,②与⑥分别是互逆命题.
C
变式1.下列三个定理中,存在逆定理的有( )
①有两个角相等的三角形是等腰三角形;
②全等三角形的对应角相等;
③同位角相等,两直线平行.
A.0个
B.1个
C.2个
D.3个
C
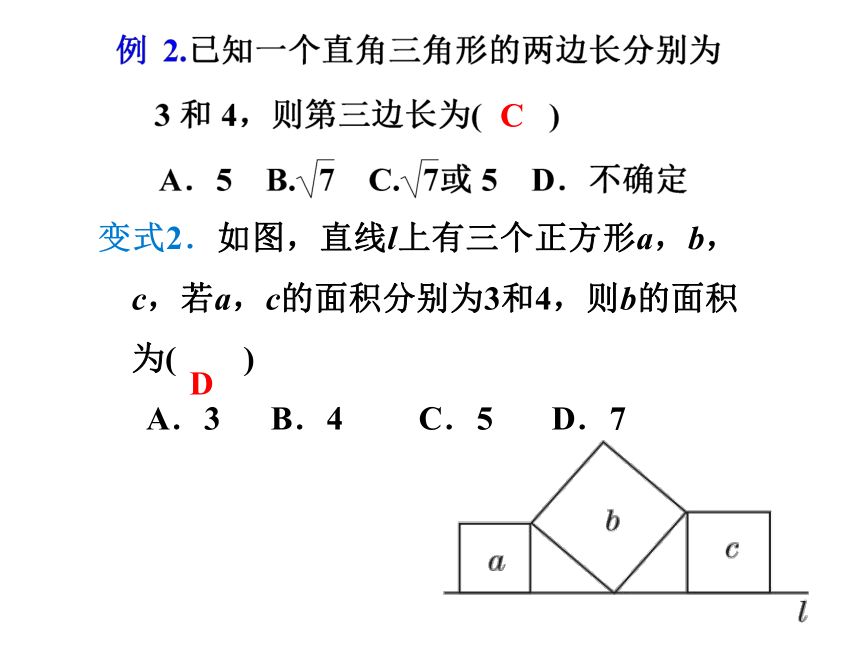
变式2.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为3和4,则b的面积为( )
A.3
B.4
C.5
D.7
D
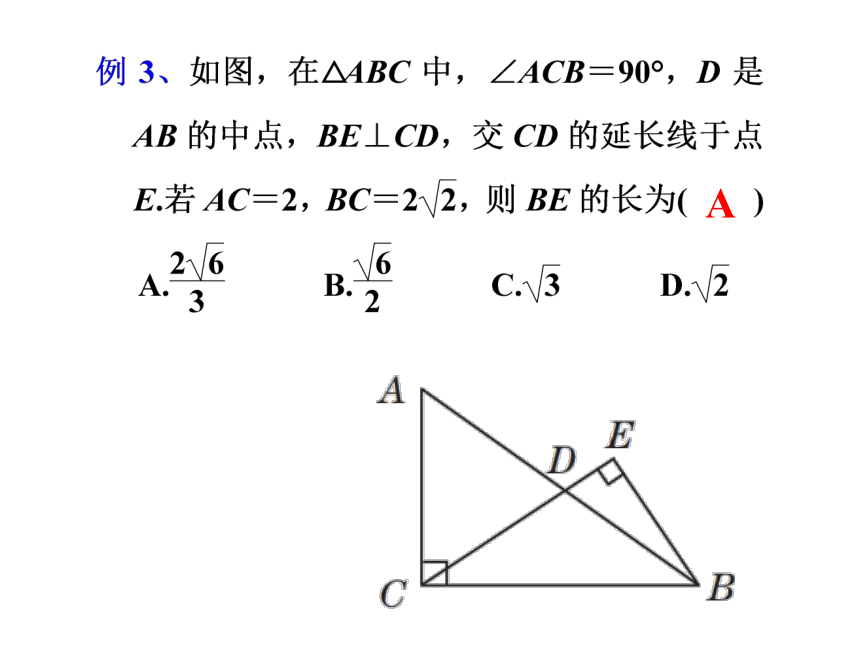
A
变式3.如图,在△ABC中,AD⊥BC,垂足为点D,∠B=60°,∠C=45°.
(1)求∠BAC的度数;
(2)若AC=2,求AD的长.
解:(1)∠BAC=180°-∠B-∠C=75°.
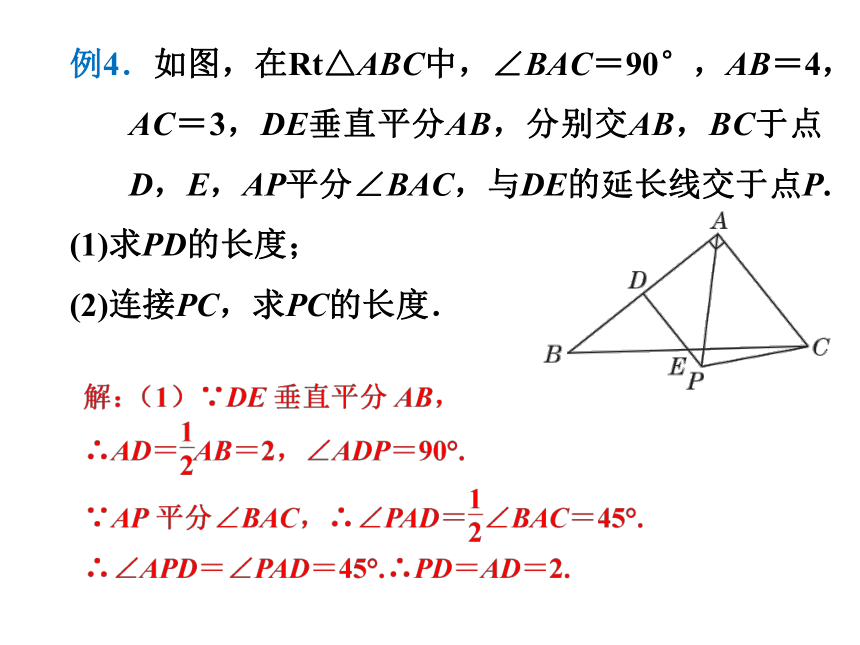
例4.如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,DE垂直平分AB,分别交AB,BC于点D,E,AP平分∠BAC,与DE的延长线交于点P.
(1)求PD的长度;
(2)连接PC,求PC的长度.
例5.如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,那么最短路径长为________.
变式5、如图,圆柱形玻璃杯高为14
cm,底面周长为32
cm,在杯内壁离杯底5
cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3
cm与蜂蜜相对的A处,则蚂蚁从外壁A处到内壁B处的最短距离为________cm(杯壁厚度不计).
20
例6、如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为( )
A.4
B.5
C.6
D.7
B
D
例7、如图,在△ABC中,∠ACB=90°,AC=BC,点P在斜边AB上,以PC为直角边作等腰直角三角形PCQ,∠PCQ=90°,则PA2,PB2,PC2三者之间的数量关系是____________________.
PB2+PA2=2PC2
D
例8、△ABC的三边长分别为a,b,c,下列条件:
①∠A=∠B-∠C;
②∠A:∠B:∠C=3:4:5;
③a2=(b+c)(b-c);
④a:b:c=5:12:13.
其中能判定△ABC是直角三角形的有( )
A.1个
B.2个
C.3个
D.4个
C
变式8.下列几组数:
①9,12,15;
②8,15,17;
③7,24,25;
④n2-1,2n,n2+1(n是大于1的整数).
其中是勾股数的有( )
A.1组
B.2组
C.3组
D.4组
D
B
变式9.如图,已知在正方形ABCD中,E是BC的中点,F在AB上,且AF:FB=3:1.
(1)请你判断EF与DE的位置关系,
并说明理由;
(2)若此正方形的面积为16,求DF的长.
第十七章
勾股定理
章末小结
知识网络
勾股定理
勾股定理的逆定理
互逆定理
直角三角形边长的数量关系
直角三角形的判定
例1.有下列命题:①直角都相等;
②内错角相等,两直线平行;
③如果a+b>0,那么a>0,b>0;
④相等的角都是直角;
⑤如果a>0,b>0,那么ab>0;
⑥两直线平行,内错角相等.
(1)③和⑤是互逆命题吗?
(2)你能说出③和⑤的逆命题各是什么吗?
(3)请指出哪几个命题是互逆命题.
解:(1)由于③的题设是a+b>0,而⑤的结论是ab>0,故⑤不是由③交换命题的题设和结论得到的,所以③和⑤不是互逆命题.
(2)能.③的逆命题是:如果a>0,b>0,那么a+b>0;⑤的逆命题是:如果ab>0,那么a>0,b>0.
(3)①与④,②与⑥分别是互逆命题.
C
变式1.下列三个定理中,存在逆定理的有( )
①有两个角相等的三角形是等腰三角形;
②全等三角形的对应角相等;
③同位角相等,两直线平行.
A.0个
B.1个
C.2个
D.3个
C
变式2.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为3和4,则b的面积为( )
A.3
B.4
C.5
D.7
D
A
变式3.如图,在△ABC中,AD⊥BC,垂足为点D,∠B=60°,∠C=45°.
(1)求∠BAC的度数;
(2)若AC=2,求AD的长.
解:(1)∠BAC=180°-∠B-∠C=75°.
例4.如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,DE垂直平分AB,分别交AB,BC于点D,E,AP平分∠BAC,与DE的延长线交于点P.
(1)求PD的长度;
(2)连接PC,求PC的长度.
例5.如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,那么最短路径长为________.
变式5、如图,圆柱形玻璃杯高为14
cm,底面周长为32
cm,在杯内壁离杯底5
cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3
cm与蜂蜜相对的A处,则蚂蚁从外壁A处到内壁B处的最短距离为________cm(杯壁厚度不计).
20
例6、如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为( )
A.4
B.5
C.6
D.7
B
D
例7、如图,在△ABC中,∠ACB=90°,AC=BC,点P在斜边AB上,以PC为直角边作等腰直角三角形PCQ,∠PCQ=90°,则PA2,PB2,PC2三者之间的数量关系是____________________.
PB2+PA2=2PC2
D
例8、△ABC的三边长分别为a,b,c,下列条件:
①∠A=∠B-∠C;
②∠A:∠B:∠C=3:4:5;
③a2=(b+c)(b-c);
④a:b:c=5:12:13.
其中能判定△ABC是直角三角形的有( )
A.1个
B.2个
C.3个
D.4个
C
变式8.下列几组数:
①9,12,15;
②8,15,17;
③7,24,25;
④n2-1,2n,n2+1(n是大于1的整数).
其中是勾股数的有( )
A.1组
B.2组
C.3组
D.4组
D
B
变式9.如图,已知在正方形ABCD中,E是BC的中点,F在AB上,且AF:FB=3:1.
(1)请你判断EF与DE的位置关系,
并说明理由;
(2)若此正方形的面积为16,求DF的长.
