四年级下册数学教案 5.2 解决问题的策略 苏教版
文档属性
| 名称 | 四年级下册数学教案 5.2 解决问题的策略 苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 366.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-22 20:42:43 | ||
图片预览

文档简介
《解决问题的策略》教学设计
教学目标:
1.掌握长度、宽度发生变化的长方形的面积的计算。
2.让学生掌握规律,能解决生活中的实际问题。
3.通过创建贴近生活的教学情境,使学生热爱数学,想学、乐学数学。
教学重难点
教学重点:掌握长方面长、宽发生变化后面积的计算。
难点:通过增加部份的面积计算出长方形长或宽从而计算原长方形(或变化后的长方面)的长和宽,进而求出相应的长方形的面积。
教学媒体:多媒体。
教学方法:同桌合作学习。
教学过程:
课前准备复习:
1.长方形面积的计算公式是什么?
生:长方形的面积=长×宽
口算练习:长是6米,宽是3米的长方形面积是多少?长是5米呢?
2.公式变形:已知长方形的面积和宽,长怎么求?已知长方形的面积和长,宽怎么求?
指名学生回答,再全班复述一遍。
长方形的面积÷长=宽 长方面的面积÷宽=长
口算长方形的长或宽:长是6米,面积是18米,宽是多少米?
创设情境,导入新课
1.师生互动,创设情境
师:大耳朵图图是一个活泼聪明的孩子,今天我们跟随图图一起去参观青少年实践基地,里面有花圃、鱼池、试验田、训练场等,可漂亮了,你们想去看看吗?
生:想
师:大家注意观察,实践基地里面的花圃、鱼池、试验田、训练场等都是什么形状呢?
生:长方形。
师:可是,实践基地里当初的设计和现在可不一样哦,我们一起去看看吧。
2.实践基地有一块长方形花圃,长8米,在修建时,花圃的长增加3米,这样花圃的面积就增加了18平方米。原来花圃的面积是多少平方米?
师:默读,思考,找到解决这个问题的办法?
生:要求原来长花圃的面积就是求长方形的面积,可是原来花圃的宽不知道,就要想办法先求出它的宽,然后用长×宽就可以算出原来花圃的面积。
师:可是原来的宽怎么求呢?有没有简便直观的方法呢?
生:可以画图。
师适时鼓励,让学生不断补充,说出怎样画,再同桌合作,把长方形花圃变形的过程画下来。
教师巡视,指导学生画图。
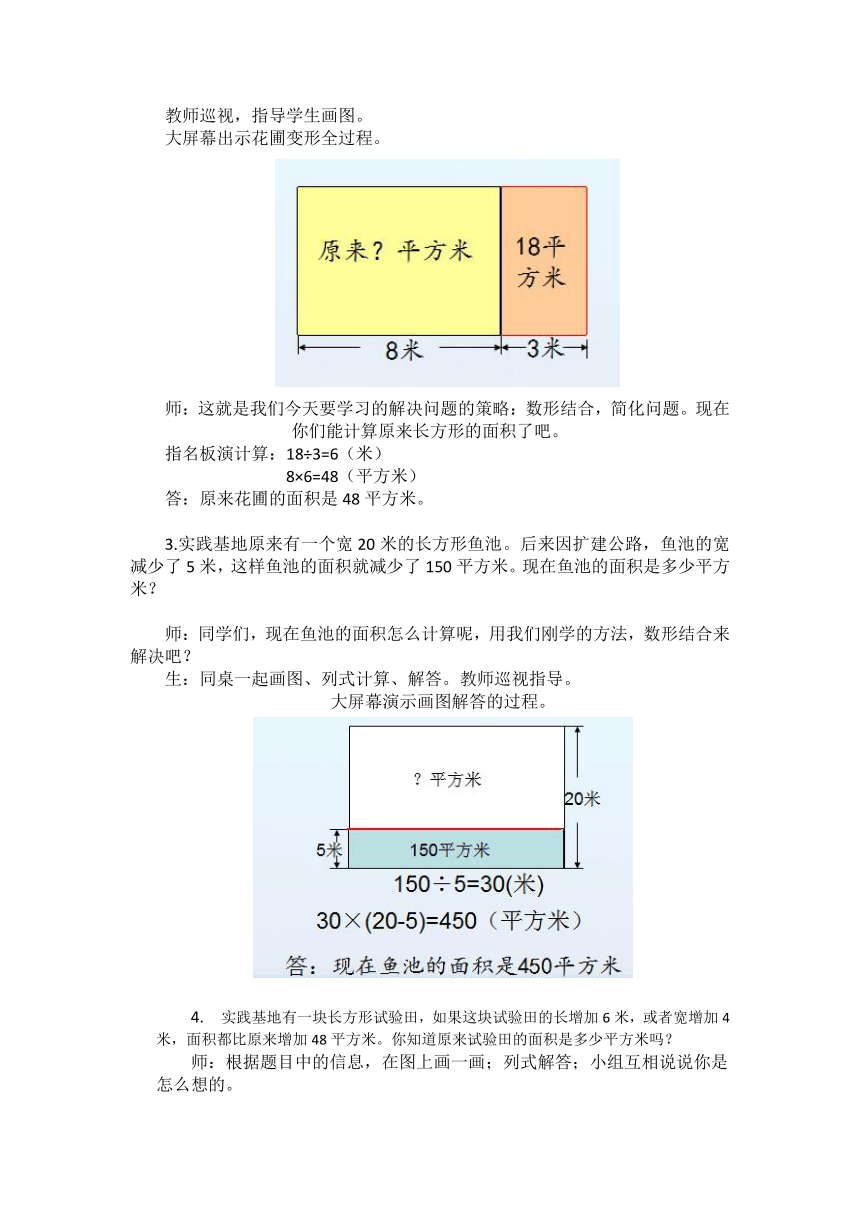
大屏幕出示花圃变形全过程。
师:这就是我们今天要学习的解决问题的策略:数形结合,简化问题。现在你们能计算原来长方形的面积了吧。
指名板演计算:18÷3=6(米)
8×6=48(平方米)
答:原来花圃的面积是48平方米。
3.实践基地原来有一个宽20米的长方形鱼池。后来因扩建公路,鱼池的宽减少了5米,这样鱼池的面积就减少了150平方米。现在鱼池的面积是多少平方米?
师:同学们,现在鱼池的面积怎么计算呢,用我们刚学的方法,数形结合来解决吧?
生:同桌一起画图、列式计算、解答。教师巡视指导。
大屏幕演示画图解答的过程。
4. 实践基地有一块长方形试验田,如果这块试验田的长增加6米,或者宽增加4米,面积都比原来增加48平方米。你知道原来试验田的面积是多少平方米吗?
师:根据题目中的信息,在图上画一画;列式解答;小组互相说说你是怎么想的。
指名回答:学生相互补充。
出示解题过程,动画演示。
5.练习:实践基地有一个长方形训练场,长50米,宽40米(如下图)。扩建时,训练场的长增加了10米,宽增加了8米。训练场的面积增加了多少平方米?
师:同学们独立完成,数形结合最容易哦。
展示学生的解题方法。
方法一:方法二:
方法三:方法四:
小结:无论哪一种方法,数形结合,都能使难题直观易解,同学们可以多用。
课堂总结:
数形结合百般好,数形隔离万事休。—华罗庚
教学目标:
1.掌握长度、宽度发生变化的长方形的面积的计算。
2.让学生掌握规律,能解决生活中的实际问题。
3.通过创建贴近生活的教学情境,使学生热爱数学,想学、乐学数学。
教学重难点
教学重点:掌握长方面长、宽发生变化后面积的计算。
难点:通过增加部份的面积计算出长方形长或宽从而计算原长方形(或变化后的长方面)的长和宽,进而求出相应的长方形的面积。
教学媒体:多媒体。
教学方法:同桌合作学习。
教学过程:
课前准备复习:
1.长方形面积的计算公式是什么?
生:长方形的面积=长×宽
口算练习:长是6米,宽是3米的长方形面积是多少?长是5米呢?
2.公式变形:已知长方形的面积和宽,长怎么求?已知长方形的面积和长,宽怎么求?
指名学生回答,再全班复述一遍。
长方形的面积÷长=宽 长方面的面积÷宽=长
口算长方形的长或宽:长是6米,面积是18米,宽是多少米?
创设情境,导入新课
1.师生互动,创设情境
师:大耳朵图图是一个活泼聪明的孩子,今天我们跟随图图一起去参观青少年实践基地,里面有花圃、鱼池、试验田、训练场等,可漂亮了,你们想去看看吗?
生:想
师:大家注意观察,实践基地里面的花圃、鱼池、试验田、训练场等都是什么形状呢?
生:长方形。
师:可是,实践基地里当初的设计和现在可不一样哦,我们一起去看看吧。
2.实践基地有一块长方形花圃,长8米,在修建时,花圃的长增加3米,这样花圃的面积就增加了18平方米。原来花圃的面积是多少平方米?
师:默读,思考,找到解决这个问题的办法?
生:要求原来长花圃的面积就是求长方形的面积,可是原来花圃的宽不知道,就要想办法先求出它的宽,然后用长×宽就可以算出原来花圃的面积。
师:可是原来的宽怎么求呢?有没有简便直观的方法呢?
生:可以画图。
师适时鼓励,让学生不断补充,说出怎样画,再同桌合作,把长方形花圃变形的过程画下来。
教师巡视,指导学生画图。
大屏幕出示花圃变形全过程。
师:这就是我们今天要学习的解决问题的策略:数形结合,简化问题。现在你们能计算原来长方形的面积了吧。
指名板演计算:18÷3=6(米)
8×6=48(平方米)
答:原来花圃的面积是48平方米。
3.实践基地原来有一个宽20米的长方形鱼池。后来因扩建公路,鱼池的宽减少了5米,这样鱼池的面积就减少了150平方米。现在鱼池的面积是多少平方米?
师:同学们,现在鱼池的面积怎么计算呢,用我们刚学的方法,数形结合来解决吧?
生:同桌一起画图、列式计算、解答。教师巡视指导。
大屏幕演示画图解答的过程。
4. 实践基地有一块长方形试验田,如果这块试验田的长增加6米,或者宽增加4米,面积都比原来增加48平方米。你知道原来试验田的面积是多少平方米吗?
师:根据题目中的信息,在图上画一画;列式解答;小组互相说说你是怎么想的。
指名回答:学生相互补充。
出示解题过程,动画演示。
5.练习:实践基地有一个长方形训练场,长50米,宽40米(如下图)。扩建时,训练场的长增加了10米,宽增加了8米。训练场的面积增加了多少平方米?
师:同学们独立完成,数形结合最容易哦。
展示学生的解题方法。
方法一:方法二:
方法三:方法四:
小结:无论哪一种方法,数形结合,都能使难题直观易解,同学们可以多用。
课堂总结:
数形结合百般好,数形隔离万事休。—华罗庚
