人教版七年级数学上册 1.1.1正数和负数、有理数、数轴 课件(共32张)
文档属性
| 名称 | 人教版七年级数学上册 1.1.1正数和负数、有理数、数轴 课件(共32张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-22 14:57:49 | ||
图片预览









文档简介
(共32张PPT)
第1讲
正数和负数
有理数、数轴
正数和负数
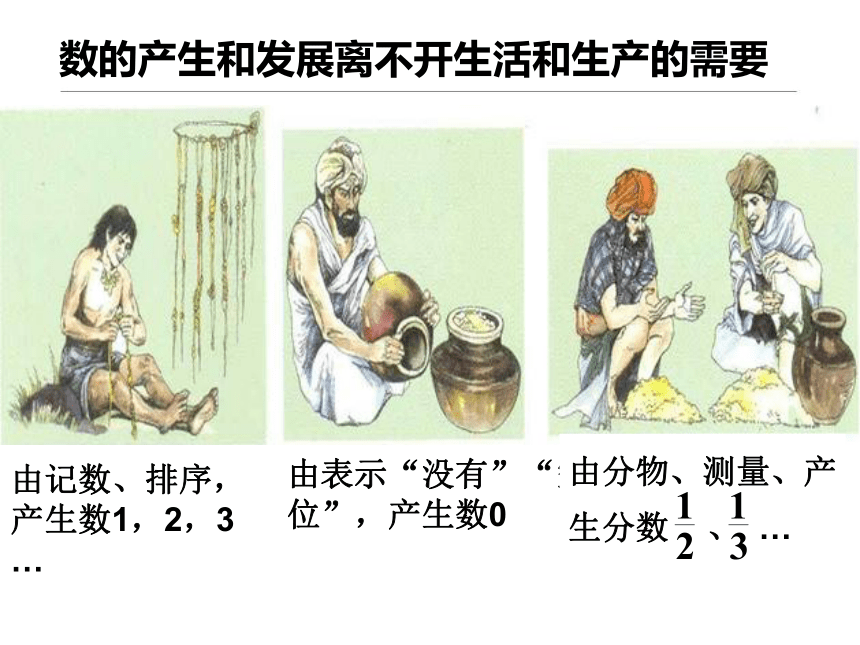
数的产生和发展离不开生活和生产的需要
由记数、排序,
产生数1,2,3
…
由表示“没有”“空
位”,产生数0
由分物、测量、产
生分数
、
…
正数和负数的概念:
正数:
像+3,+1.8%,+3.5
这样大于0的数
负数:
像-3,-2.7%,-4.5
这样在正数前加上符号
“-”(负号)的数。
即:小于0的数
①一个数前面
的“+”“-”号叫
做它的符号
强调:
②0既不是正数
也不是负数
正数和负数的应用:
表示具有相反意义的量
上升
下降
零上
零下
前进
后退
收入
支出
增加
减少
5m
3m
8℃
2℃
4m
6m
100元
30元
6kg
3kg
+5m
-3m
+8℃
-2℃
+4m
-6m
+100元
-30元
+6kg
-3kg
强调:
1、对于两个具有相反意义的量,把哪一种意
义规定为正,带有任意性
2、习惯上把向东、上升、盈利、运进、增加、
收入、前进、高出、零上等规定为正;把
它们的相反意义的量规定为负。
练习:
1、如果收入300元用+300元表示,那么支出200元可以表示为________
2、如果零上6℃记作+6
℃,那么零下10
℃记作_______
练习:
4、下列不是具有相反意义的量的是(
)
A.向前移动3m和向后移动3m
B.节约3t和浪费10t
C.身高增加3cm和体重减少3kg
D.上升5m和下降2m
3、某仓库运进面粉7.5吨记作+7.5吨,
那
么-3.8吨表示_________________
例题1:
一个月内,张丹体重增加2kg,王娜体重
减少1kg,林燕体重无变化。写出他们这个月
的体重增长值。
增加2kg和减少1kg是具有相反意义的量
体重增长值可能是正的,也
可能是负的,还可能是0,增长值为负数,相当于体重减少,增长值为0,相当于体重无变化。
例题2:
某年下列国家的商品进出口总额比
上年的变化情况是:
美国减少6.4%,
德国增长1.3%,
法国减少2.4%,
英国减少3.5%,
意大利增长0.2%,
中国增长7.5%.
写出这些国家这一年商品进出口总额的增长率.
例题3:
摩托车厂本周计划每天生产250辆摩托车,
由于工人实行轮休,每天上班的人数不一定相等,
实际每天生产量(与计划量相比)的增长值如表:
星期
一
二
三
四
五
六
日
增长值
-5
+7
-3
+4
+10
-9
-25
根据上面的记录,问:哪几天生产的摩托车比计划量多?星期几生产的摩托车最多,是多少辆?星期几生产的摩托车最少,是多少辆?
有理数
有理数的概念:
1,18,35…
正整数:
负整数:
-5,-13,-20…
零
正分数:
,20%,0.15…
负分数:
,-35%,-0.5…
整数
分数
整数和分数统称为有理数
特别强调:
REPORT
2018
1、由于有限小数、无限循环小数、百分数均
可以化成分数的形式,所以属于分数。
2、π是无限不循环小数,既不是整数,也不
是分数,更不是有理数,但π是正数,也是无
理数。
有理数的分类:
1、将有理数按定义(整数、分数)分类:
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数的分类:
2、将有理数按数的符号(+、-)分类:
有理数
正有理数
负有理数
正整数
零
正分数
负整数
负分数
拓展:
非负数:
非正数:
即:不是负数
包括:正数和0
即:不是正数
包括:负数和0
练习:
把下列各数填入相应集合的括号内:
π
,-3.1416,0,2017,
,-0.23,10%
10.1,-89,
正整数集合:{
}
负分数集合:{
}
正数集合:{
}
分数集合:{
}
非负数集合:{
}
有理数集合:{
}
数轴
问题:
在一条东西向的马路上,有一个汽车站,
汽车站东3m和7.5m处分别有一棵柳树和一棵杨
树,汽车站西3m和4.8m处分别有一棵槐树和一
根电线杆,试画图表示这一情境.
西
东
o
A
B
C
D
E
3m
7.5m
3m
4.8m
西
东
o
A
B
C
D
E
3m
7.5m
3m
4.8m
思考:
思考:
如何用数表示这些树、电线杆与汽
车站牌的相对位置呢?
o
A
B
C
D
E
0
1
3
7.5
-3
-4.8
数轴的概念:
规定了原点、正方向和单位长度的直线
叫做数轴.
数轴的三要素
数轴的画法:
0
1
2
3
-1
-2
-3
(2)在直线上选取适当的一点为原点
(3)通常规定向右为正方向,用箭头表示
(4)选取适当的长度为单位长度
(1)画一条水平的直线
特别强调:
0
1
2
3
-1
-2
-3
1、原点的位置的确定和单位长度的大小,可
以根据问题的实际需要,灵活选取,一般是
0.5cm或1cm。
2、同一个数轴上的单位长度必须统一,不能
出现不同的单位长度表示相同的数量;
3、数轴的两端不能画点,两端画点数轴就成
线段或射线了.
练习:
1、判断下面所画数轴是否正确,并说明理由。
练习:
2、请先画出一个数轴,并用数轴上的点表示
下列各数:
,-5,0,-4,3,-
3、指出数轴上A,B,C,D各点分别表示什
么数.
0
1
2
3
-1
-2
A
D
C
B
归纳总结:
一般地,设a是一个正数,则数轴上表
示数a的点在原点的____边,与原点的距离
是____个单位长度;
表示数-a的点在原点
的____边,与原点的距离是____个单位长度.
REPORT
2018
右
a
左
a
谢谢!
如果把每月生产180个零件记作0个,则一月加工160个零件记作______个,二月加工200个零件记作______个.
变式1:
规定向东为正,小明走了+5千米后,又继续走了-10千米,那么小明实际上(
)
A.向西走了15?千米
B.向东走了15?千米
C.向西走了5?千米
D.向东走了5千米
变式2:
在一次数学测试中,我采用了一种“秘密”记分法:小明得92分,记作+7分,小张得80分,记作﹣5分.若小强的得分计作+3分,那么小强的实际得分为______分.
变式3:
探索规律
观察下列一组数据:
(1)第2019个数是多少?
(2)试表达第n个数是多少?(用含n的式子表述)
第1讲
正数和负数
有理数、数轴
正数和负数
数的产生和发展离不开生活和生产的需要
由记数、排序,
产生数1,2,3
…
由表示“没有”“空
位”,产生数0
由分物、测量、产
生分数
、
…
正数和负数的概念:
正数:
像+3,+1.8%,+3.5
这样大于0的数
负数:
像-3,-2.7%,-4.5
这样在正数前加上符号
“-”(负号)的数。
即:小于0的数
①一个数前面
的“+”“-”号叫
做它的符号
强调:
②0既不是正数
也不是负数
正数和负数的应用:
表示具有相反意义的量
上升
下降
零上
零下
前进
后退
收入
支出
增加
减少
5m
3m
8℃
2℃
4m
6m
100元
30元
6kg
3kg
+5m
-3m
+8℃
-2℃
+4m
-6m
+100元
-30元
+6kg
-3kg
强调:
1、对于两个具有相反意义的量,把哪一种意
义规定为正,带有任意性
2、习惯上把向东、上升、盈利、运进、增加、
收入、前进、高出、零上等规定为正;把
它们的相反意义的量规定为负。
练习:
1、如果收入300元用+300元表示,那么支出200元可以表示为________
2、如果零上6℃记作+6
℃,那么零下10
℃记作_______
练习:
4、下列不是具有相反意义的量的是(
)
A.向前移动3m和向后移动3m
B.节约3t和浪费10t
C.身高增加3cm和体重减少3kg
D.上升5m和下降2m
3、某仓库运进面粉7.5吨记作+7.5吨,
那
么-3.8吨表示_________________
例题1:
一个月内,张丹体重增加2kg,王娜体重
减少1kg,林燕体重无变化。写出他们这个月
的体重增长值。
增加2kg和减少1kg是具有相反意义的量
体重增长值可能是正的,也
可能是负的,还可能是0,增长值为负数,相当于体重减少,增长值为0,相当于体重无变化。
例题2:
某年下列国家的商品进出口总额比
上年的变化情况是:
美国减少6.4%,
德国增长1.3%,
法国减少2.4%,
英国减少3.5%,
意大利增长0.2%,
中国增长7.5%.
写出这些国家这一年商品进出口总额的增长率.
例题3:
摩托车厂本周计划每天生产250辆摩托车,
由于工人实行轮休,每天上班的人数不一定相等,
实际每天生产量(与计划量相比)的增长值如表:
星期
一
二
三
四
五
六
日
增长值
-5
+7
-3
+4
+10
-9
-25
根据上面的记录,问:哪几天生产的摩托车比计划量多?星期几生产的摩托车最多,是多少辆?星期几生产的摩托车最少,是多少辆?
有理数
有理数的概念:
1,18,35…
正整数:
负整数:
-5,-13,-20…
零
正分数:
,20%,0.15…
负分数:
,-35%,-0.5…
整数
分数
整数和分数统称为有理数
特别强调:
REPORT
2018
1、由于有限小数、无限循环小数、百分数均
可以化成分数的形式,所以属于分数。
2、π是无限不循环小数,既不是整数,也不
是分数,更不是有理数,但π是正数,也是无
理数。
有理数的分类:
1、将有理数按定义(整数、分数)分类:
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数的分类:
2、将有理数按数的符号(+、-)分类:
有理数
正有理数
负有理数
正整数
零
正分数
负整数
负分数
拓展:
非负数:
非正数:
即:不是负数
包括:正数和0
即:不是正数
包括:负数和0
练习:
把下列各数填入相应集合的括号内:
π
,-3.1416,0,2017,
,-0.23,10%
10.1,-89,
正整数集合:{
}
负分数集合:{
}
正数集合:{
}
分数集合:{
}
非负数集合:{
}
有理数集合:{
}
数轴
问题:
在一条东西向的马路上,有一个汽车站,
汽车站东3m和7.5m处分别有一棵柳树和一棵杨
树,汽车站西3m和4.8m处分别有一棵槐树和一
根电线杆,试画图表示这一情境.
西
东
o
A
B
C
D
E
3m
7.5m
3m
4.8m
西
东
o
A
B
C
D
E
3m
7.5m
3m
4.8m
思考:
思考:
如何用数表示这些树、电线杆与汽
车站牌的相对位置呢?
o
A
B
C
D
E
0
1
3
7.5
-3
-4.8
数轴的概念:
规定了原点、正方向和单位长度的直线
叫做数轴.
数轴的三要素
数轴的画法:
0
1
2
3
-1
-2
-3
(2)在直线上选取适当的一点为原点
(3)通常规定向右为正方向,用箭头表示
(4)选取适当的长度为单位长度
(1)画一条水平的直线
特别强调:
0
1
2
3
-1
-2
-3
1、原点的位置的确定和单位长度的大小,可
以根据问题的实际需要,灵活选取,一般是
0.5cm或1cm。
2、同一个数轴上的单位长度必须统一,不能
出现不同的单位长度表示相同的数量;
3、数轴的两端不能画点,两端画点数轴就成
线段或射线了.
练习:
1、判断下面所画数轴是否正确,并说明理由。
练习:
2、请先画出一个数轴,并用数轴上的点表示
下列各数:
,-5,0,-4,3,-
3、指出数轴上A,B,C,D各点分别表示什
么数.
0
1
2
3
-1
-2
A
D
C
B
归纳总结:
一般地,设a是一个正数,则数轴上表
示数a的点在原点的____边,与原点的距离
是____个单位长度;
表示数-a的点在原点
的____边,与原点的距离是____个单位长度.
REPORT
2018
右
a
左
a
谢谢!
如果把每月生产180个零件记作0个,则一月加工160个零件记作______个,二月加工200个零件记作______个.
变式1:
规定向东为正,小明走了+5千米后,又继续走了-10千米,那么小明实际上(
)
A.向西走了15?千米
B.向东走了15?千米
C.向西走了5?千米
D.向东走了5千米
变式2:
在一次数学测试中,我采用了一种“秘密”记分法:小明得92分,记作+7分,小张得80分,记作﹣5分.若小强的得分计作+3分,那么小强的实际得分为______分.
变式3:
探索规律
观察下列一组数据:
(1)第2019个数是多少?
(2)试表达第n个数是多少?(用含n的式子表述)
