北师大版七年级数学下册4.2图形的全等 课件(18张)
文档属性
| 名称 | 北师大版七年级数学下册4.2图形的全等 课件(18张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 652.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-23 14:31:19 | ||
图片预览






文档简介
4.2图形的全等
每日一语:山不厌高,海不厌深,周公吐哺,天下归心。
选择我所爱,爱我所选择~
教学目标
1、通过实例理解图形全等的概念和特征,并能识别图形的全等。
2、掌握全等三角形对应边相等,对应角相等的性质,并能进行简单的推理和计算,解决一些实际问题。
教学重难点
1、重点:全等三角形的性质的掌握与应用。
2、难点:正确识别全等三角形的对应元素。
你能再举出一些例子吗?
欣赏图片
这些图片有何特征?
导读提纲
一、导读提纲
同一张底片洗出的相同尺寸的照片,有什么特点呢?
它们的形状、大小相同,能够完全重合.
能够完全重合的两个图形称为全等图形.
观察下面三组图形,它们是不是全等图形?为什么?与同伴进行交流.
(1)
(2)
(3)
全等图形的形状一定相同,大小一定相等.
表示时通常把对应顶点的字母写在对应的位置上.
△ABC≌△DEF
记作: △ABC ≌ △DEF
读作: △ ABC全等于△ DEF
A
B
C
D
E
F
想一想
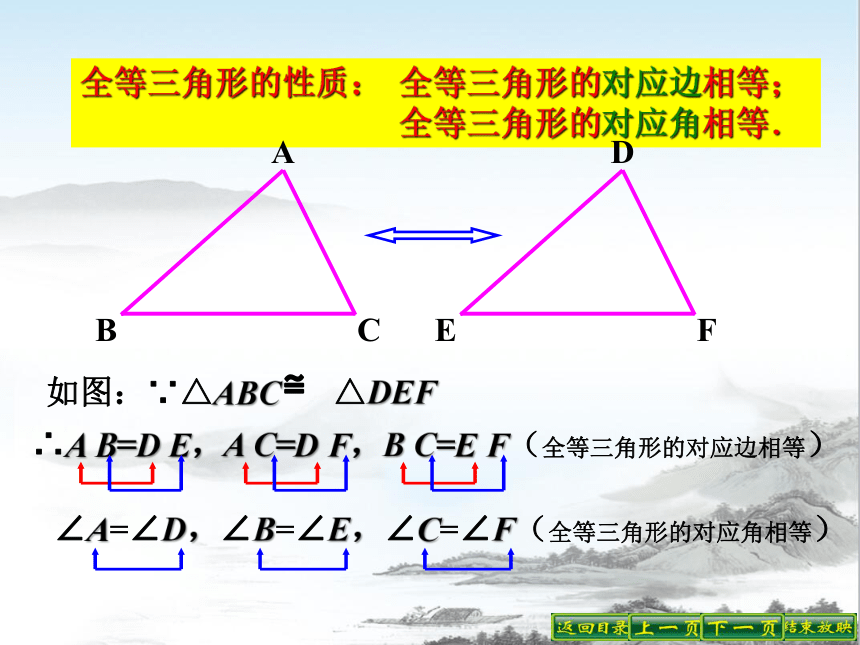
如图:∵△ABC≌△DEF
∴A B=D E,A C=D F,B C=E F(全等三角形的对应边相等)
全等三角形的性质: 全等三角形的对应边相等;
全等三角形的对应角相等.
∠A=∠D,∠B=∠E,∠C=∠F(全等三角形的对应角相等)
A
B
C
D
E
F
A
B
C
1、能够完全重合的两个三角形叫做_______________,如下图,△ABC与△DEF全等,记作__________________,通常把表示对应顶点的字母写在________的位置上。
2、如上图,顶点A、D重合,它们是_______顶点,点B与点______,点_____与点F是对应顶点;AB边与DE边重合,它们是__________,BC的对应边是_______,________的对应边是DF;∠A与∠D重合,它们是__________,∠B的对应角是_______,∠F的对应角是________。
D
E
F
全等三角形
△ABC≌△DEF
对应
对应
E
C
对应边
EF
AC
对应角
∠E
∠C
当堂检测
1、判断题
(1)两个形状相同的图形,称为全等图形。( )
(2)两个圆是全等图形。( )
(3)两个正方形是全等图形。( )
(4)全等图形的形状和大小都相同。( )
(5)面积相同的两个直角三角形是全等图形。( )
2、由同一张底片冲洗出来的两张五寸照片的图案 —— 全等图形,而由同一张底片冲洗出来的五寸照片和七寸照片 全等图形(填“是”或“不是”)。
×
×
√
×
×
是
不是
二、基础知识检测与过关
3.如图,△ABC ≌ △AEC,∠B = 30° ,∠ACB = 85°,则∠E=_____,∠ACE=_____,∠EAC=______。
30°
85°
65°
二、基础知识检测与过关
1、如图,已知△ABC≌△DFE,你能写出它们的对应边和对应角吗?
对应边:AB与DF,
BC与FE,
AC与DE
对应角:∠A与 ∠D,
∠B与∠F,
∠ACB与∠DEF
三、重难点的精讲:
解:∵ △ACF≌△DBE
∴AC=DB
∴AC-BC=DB-BC
即AB=DC
2、如图所示,已知△ACF≌△DBE,∠F=∠E,AD=10cm,BC=6cm,求AB的长。
三、重难点的精讲:
2、如图所示,△ABC≌△DBE,AB⊥BC,DE的延长线交AC于点F。试判断DF与AC的位置关系,并说明理由。
解:DF⊥AC
理由:∵ △ABC≌△DBE
∴∠C=∠1
∵∠1=∠2
∴∠2=∠C
∵ AB⊥BC
∴∠A+∠C=90°
∴∠A+∠2=90°
∴∠AFE=90°
即DF⊥AC
四、重难点知识的分层应用
2.我校要修一座等边三角形花坛
(右图),有这么几种方案:
1、把它分成两个全等的三角形;
2、把它分成三个全等的三角形;
3、把它分成四个全等的三角形;
并在分成的全等三角形中种上不同颜色的花,你赞成哪种方案?请绘出你的平面效果图,大家评一评,看谁的方案最漂亮?
四、重难点知识的分层应用
小结
1、能够完全重合的两个图形称为全等图形.
2、全等三角形的性质: 全等三角形的对应边相等;
全等三角形的对应角相等.
1、判断题
(1)只有两个三角形才能完全重合;( )
(2)如果两个图形全等,它们的形状和大小一定都相同;( )
(3)两个正方形一定是全等形;( )
(4)边数相同的图形一定能互相重合. ( )
2、把大小4×4的正方形方格图形分割成两个全等图形,例如,图1,请在其它图中,沿着虚线画出四种不同的分法,把4×4的正方形方格图形分割成两个全等图形.
3、请至少用2种方法将下面一个大菱形分成4个全等的图形。
×
×
×
√
五、分层作业布置:
谢谢聆听!
每日一语:山不厌高,海不厌深,周公吐哺,天下归心。
选择我所爱,爱我所选择~
教学目标
1、通过实例理解图形全等的概念和特征,并能识别图形的全等。
2、掌握全等三角形对应边相等,对应角相等的性质,并能进行简单的推理和计算,解决一些实际问题。
教学重难点
1、重点:全等三角形的性质的掌握与应用。
2、难点:正确识别全等三角形的对应元素。
你能再举出一些例子吗?
欣赏图片
这些图片有何特征?
导读提纲
一、导读提纲
同一张底片洗出的相同尺寸的照片,有什么特点呢?
它们的形状、大小相同,能够完全重合.
能够完全重合的两个图形称为全等图形.
观察下面三组图形,它们是不是全等图形?为什么?与同伴进行交流.
(1)
(2)
(3)
全等图形的形状一定相同,大小一定相等.
表示时通常把对应顶点的字母写在对应的位置上.
△ABC≌△DEF
记作: △ABC ≌ △DEF
读作: △ ABC全等于△ DEF
A
B
C
D
E
F
想一想
如图:∵△ABC≌△DEF
∴A B=D E,A C=D F,B C=E F(全等三角形的对应边相等)
全等三角形的性质: 全等三角形的对应边相等;
全等三角形的对应角相等.
∠A=∠D,∠B=∠E,∠C=∠F(全等三角形的对应角相等)
A
B
C
D
E
F
A
B
C
1、能够完全重合的两个三角形叫做_______________,如下图,△ABC与△DEF全等,记作__________________,通常把表示对应顶点的字母写在________的位置上。
2、如上图,顶点A、D重合,它们是_______顶点,点B与点______,点_____与点F是对应顶点;AB边与DE边重合,它们是__________,BC的对应边是_______,________的对应边是DF;∠A与∠D重合,它们是__________,∠B的对应角是_______,∠F的对应角是________。
D
E
F
全等三角形
△ABC≌△DEF
对应
对应
E
C
对应边
EF
AC
对应角
∠E
∠C
当堂检测
1、判断题
(1)两个形状相同的图形,称为全等图形。( )
(2)两个圆是全等图形。( )
(3)两个正方形是全等图形。( )
(4)全等图形的形状和大小都相同。( )
(5)面积相同的两个直角三角形是全等图形。( )
2、由同一张底片冲洗出来的两张五寸照片的图案 —— 全等图形,而由同一张底片冲洗出来的五寸照片和七寸照片 全等图形(填“是”或“不是”)。
×
×
√
×
×
是
不是
二、基础知识检测与过关
3.如图,△ABC ≌ △AEC,∠B = 30° ,∠ACB = 85°,则∠E=_____,∠ACE=_____,∠EAC=______。
30°
85°
65°
二、基础知识检测与过关
1、如图,已知△ABC≌△DFE,你能写出它们的对应边和对应角吗?
对应边:AB与DF,
BC与FE,
AC与DE
对应角:∠A与 ∠D,
∠B与∠F,
∠ACB与∠DEF
三、重难点的精讲:
解:∵ △ACF≌△DBE
∴AC=DB
∴AC-BC=DB-BC
即AB=DC
2、如图所示,已知△ACF≌△DBE,∠F=∠E,AD=10cm,BC=6cm,求AB的长。
三、重难点的精讲:
2、如图所示,△ABC≌△DBE,AB⊥BC,DE的延长线交AC于点F。试判断DF与AC的位置关系,并说明理由。
解:DF⊥AC
理由:∵ △ABC≌△DBE
∴∠C=∠1
∵∠1=∠2
∴∠2=∠C
∵ AB⊥BC
∴∠A+∠C=90°
∴∠A+∠2=90°
∴∠AFE=90°
即DF⊥AC
四、重难点知识的分层应用
2.我校要修一座等边三角形花坛
(右图),有这么几种方案:
1、把它分成两个全等的三角形;
2、把它分成三个全等的三角形;
3、把它分成四个全等的三角形;
并在分成的全等三角形中种上不同颜色的花,你赞成哪种方案?请绘出你的平面效果图,大家评一评,看谁的方案最漂亮?
四、重难点知识的分层应用
小结
1、能够完全重合的两个图形称为全等图形.
2、全等三角形的性质: 全等三角形的对应边相等;
全等三角形的对应角相等.
1、判断题
(1)只有两个三角形才能完全重合;( )
(2)如果两个图形全等,它们的形状和大小一定都相同;( )
(3)两个正方形一定是全等形;( )
(4)边数相同的图形一定能互相重合. ( )
2、把大小4×4的正方形方格图形分割成两个全等图形,例如,图1,请在其它图中,沿着虚线画出四种不同的分法,把4×4的正方形方格图形分割成两个全等图形.
3、请至少用2种方法将下面一个大菱形分成4个全等的图形。
×
×
×
√
五、分层作业布置:
谢谢聆听!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
