《勾股定理》第二课时导学案(无答案)
文档属性
| 名称 | 《勾股定理》第二课时导学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 95.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-13 00:00:00 | ||
图片预览

文档简介
《勾股定理》第二课时导学案
年级:八年级 学科:数学 姓名
教学目标:1、知识目标:在上一节课学习了勾股定理的基础上,联系实际,应用勾股定理解决问题。
2、能力目标:经过观察——分析——讨论——归纳的过程,发展学生自我分析、归纳,解决问题的能力。
3、情感目标:通过问题的解决,让学生了解勾股定理的广泛应用,感受数学在实际生活中无处不在。
教学重点:应用勾股定理解决相关问题。
教学难点:将实际问题转化为数学问题。
【自学指导】:
一 、相信你还记得
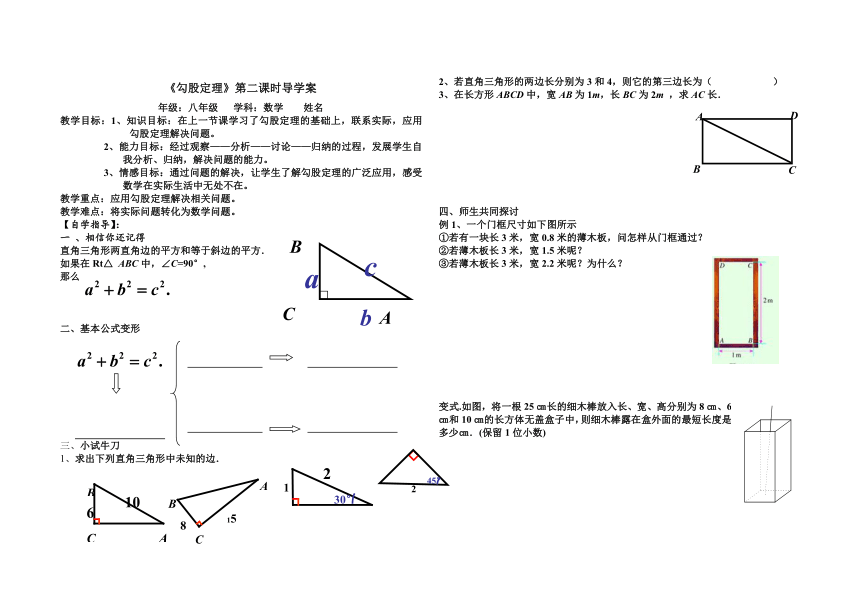
直角三角形两直角边的平方和等于斜边的平方.
如果在Rt△ ABC中,∠C=90°,
那么
二、基本公式变形
三、小试牛刀
1、求出下列直角三角形中未知的边.
2、若直角三角形的两边长分别为3和4,则它的第三边长为( )
3、在长方形ABCD中,宽AB为1m,长BC为2m ,求AC长.
四、师生共同探讨
例1、一个门框尺寸如下图所示
①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过?
②若薄木板长3米,宽1.5米呢?
③若薄木板长3米,宽2.2米呢?为什么?
变式.如图,将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和10㎝的长方体无盖盒子中,则细木棒露在盒外面的最短长度是多少㎝.(保留1位小数)
例2、一个2.5m长的梯子AB斜靠在一竖直的墙AC上,这时AC的距离为2.4m.如果梯子顶端A沿墙下滑0.4m,那么梯子底端B也外移0.4m吗?
变式:如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
例3、在一个圆柱石凳上,若小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想从A 处爬向B处,你们想一想,蚂蚁怎么走最近?若已知圆柱体高为12cm,底面半径为3cm,π取3,蚂蚁走了多远?
变式:如图,在棱长为10厘米的正方体的一个顶点A处有一只蚂蚁,现要向顶点B处爬行,蚂蚁爬行的最短距离是多少?
a
b
c
A
B
C
2
45°
30°
1
2
8
A
15
C
B
6
10
A
C
B
A
C
B
D
A
B
B
食物
A
年级:八年级 学科:数学 姓名
教学目标:1、知识目标:在上一节课学习了勾股定理的基础上,联系实际,应用勾股定理解决问题。
2、能力目标:经过观察——分析——讨论——归纳的过程,发展学生自我分析、归纳,解决问题的能力。
3、情感目标:通过问题的解决,让学生了解勾股定理的广泛应用,感受数学在实际生活中无处不在。
教学重点:应用勾股定理解决相关问题。
教学难点:将实际问题转化为数学问题。
【自学指导】:
一 、相信你还记得
直角三角形两直角边的平方和等于斜边的平方.
如果在Rt△ ABC中,∠C=90°,
那么
二、基本公式变形
三、小试牛刀
1、求出下列直角三角形中未知的边.
2、若直角三角形的两边长分别为3和4,则它的第三边长为( )
3、在长方形ABCD中,宽AB为1m,长BC为2m ,求AC长.
四、师生共同探讨
例1、一个门框尺寸如下图所示
①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过?
②若薄木板长3米,宽1.5米呢?
③若薄木板长3米,宽2.2米呢?为什么?
变式.如图,将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和10㎝的长方体无盖盒子中,则细木棒露在盒外面的最短长度是多少㎝.(保留1位小数)
例2、一个2.5m长的梯子AB斜靠在一竖直的墙AC上,这时AC的距离为2.4m.如果梯子顶端A沿墙下滑0.4m,那么梯子底端B也外移0.4m吗?
变式:如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
例3、在一个圆柱石凳上,若小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想从A 处爬向B处,你们想一想,蚂蚁怎么走最近?若已知圆柱体高为12cm,底面半径为3cm,π取3,蚂蚁走了多远?
变式:如图,在棱长为10厘米的正方体的一个顶点A处有一只蚂蚁,现要向顶点B处爬行,蚂蚁爬行的最短距离是多少?
a
b
c
A
B
C
2
45°
30°
1
2
8
A
15
C
B
6
10
A
C
B
A
C
B
D
A
B
B
食物
A
