北师大版八下数学第六章6.3三角形的中位线同步练习(word版含答案)
文档属性
| 名称 | 北师大版八下数学第六章6.3三角形的中位线同步练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 820.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-22 19:53:41 | ||
图片预览



文档简介
第六章三角形的中位线
一、选择题(共5小题;共25分)
1.
如图,在四边形
中,
是对角线
的中点,,
分别是
,
的中点,,,则
的度数是
A.
B.
C.
D.
2.
已知四边形ABCD中,,
分别是
,
上的点,,
分别是
,
的中点,当点
在
上从
向
移动而点
不动时,那么下列结论成立的是
A.
线段
的长逐渐增大
B.
线段
的长逐渐减小
C.
线段
的长不变
D.
线段
的长与点
的位置有关
3.
如图,
中,,,
、
分别是其角平分线和中线,过点
作
于
,交
于
,连接
,则线段
的长为
A.
B.
C.
D.
4.
如图,
的周长为
,点
,
都在边
上,
的平分线垂直于
,垂足为
,
的平分线垂直于
,垂足为
.若
,则
的长为
A.
B.
C.
D.
5.
小明爸爸的风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如图所示的风筝,点
,,,
分别是四边形
各边的中点.其中阴影部分用甲布料,其余部分用乙布料(裁剪两种布料时,均不计余料).若生产这批风筝需要甲布料
匹,那么需要乙布料
A.
匹
B.
匹
C.
匹
D.
匹
二、填空题(共5小题;共25分)
6.
如图,,
两地被一座小山阻隔,为测量
,
两地之间的距离,在地面上选一点
,连接
,,分别取
,
的中点
,,测得
的长度为
米,则
,
两地之间的距离是
?
米.
7.
如图,在
中,,,,
分别是
,,
的中点,若
,则
?
.
8.
如图,平行四边形
的周长为
,对角线
,
相交于点
.点
是
的中点,,则
的周长为
?.
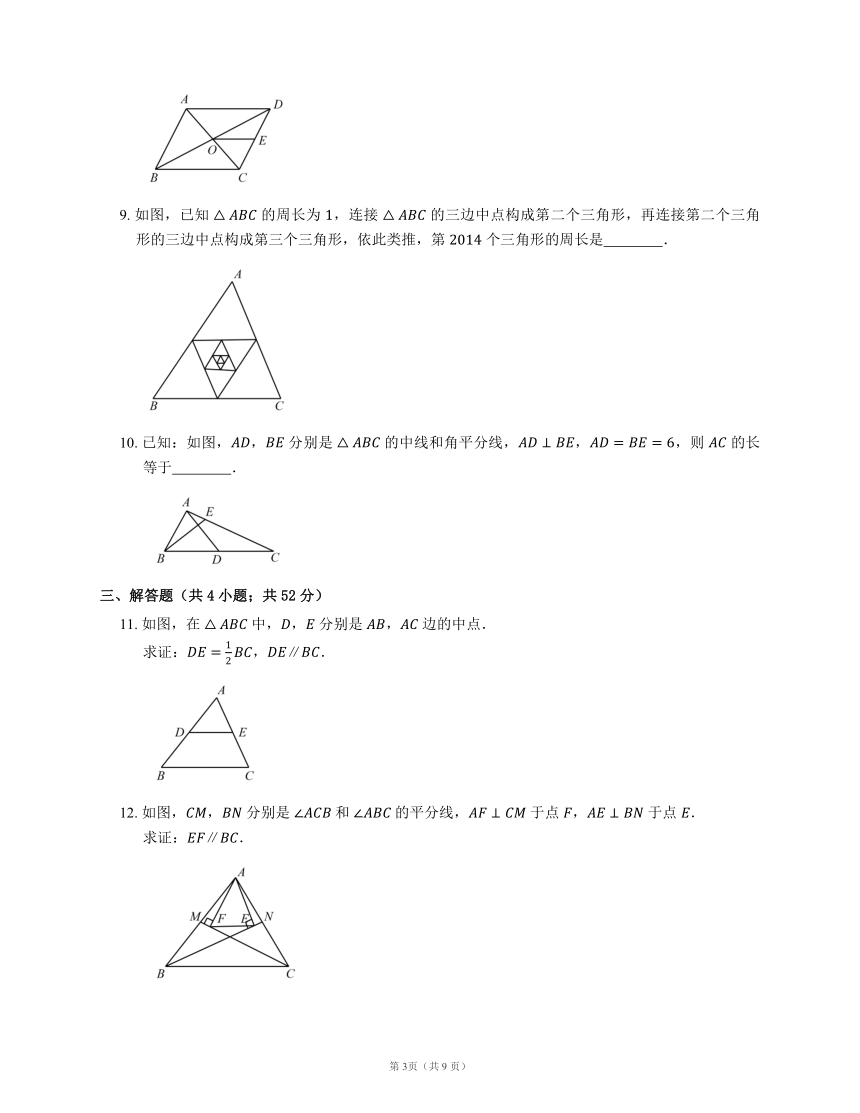
9.
如图,已知
的周长为
,连接
的三边中点构成第二个三角形,再连接第二个三角形的三边中点构成第三个三角形,依此类推,第
个三角形的周长是
?.
10.
已知:如图,,
分别是
的中线和角平分线,,,则
的长等于
?.
三、解答题(共4小题;共52分)
11.
如图,在
中,,
分别是
,
边的中点.
求证:,.
12.
如图,,
分别是
和
的平分线,
于点
,
于点
.
求证:.
13.
如图,点
是
内一点,连接
、
,并将
、
、
、
的中点
、
、
、
依次连接,得到四边形
.
(1)求证:四边形
是平行四边形;
(2)若
为
的中点,,
和
互余,求
的长度.
14.
(1)方法回顾
在学习三角形中位线时,为了探索三角形中位线的性质,思路如下:
第一步添加辅助线:如图
1,在
中,延长
(,
分别是
,
的中点)到点
,使得
,连接
;
第二步证明
,再证四边形
是平行四边形,从而得到
,.
(1)问题解决
如图
2,在正方形
中,
为
的中点,,
分别为
,
边上的点,若
,,,求
的长.
(2)拓展研究
如图
3,在四边形
中,,,
为
的中点,,
分别为
,
边上的点,若
,,,求
的长.
答案
1.
C
【解析】
在四边形
中,
是对角线
的中点,,
分别是
,
的中点,,
分别是
与
的中位线,,.,.故
是等腰三角形.,.
2.
C
【解析】连接
,由三角形中位线定理可知在
点的运动过程中,
一定等于
的一半.又由于
的长不变,所以可做出正确的判断.
3.
A
【解析】
是
的平分线,.又
,,..在
中,
为
的中点,
为
的中点,.
4.
C
【解析】由题意,,,.
,.
.
.
.
5.
C
【解析】先连接
,,利用三角形中位线定理.可得
,同理,可得
,,,四个式子相加,可得空白的四个三角形的面积和等于四边形
面积的一半,于是可得阴影部分面积等于空白部分四个三角形的面积,那么所需甲乙布料相等,即乙也需
匹.
6.
7.
8.
【解析】提示:由题意可知
的周长
.
9.
【解析】由三角形的中位线定理,第二个三角形的各边分别为
各边的一半,
第二个三角形的周长是
周长的
,即
,第三个三角形的周长是第二个三角形周长的
,即
,第四个三角形的周长是第三个三角形周长的
,即
以此类推,第
个三角形的周长是
.
10.
【解析】
如图,延长
至
,令
,连接
,过点
作
交
的延长线于点
,过点
作
交
于
.
是
的角平分线,,
,.
易得
,
,
又
,
四边形
为平行四边形.
,
,
.
在
中,
.
可证
,
,
,
,
.
11.
延长
到点
使
,连接
.
在
中,
,
,
,,
又
,
,
四边形
为平行四边形.
,,即
,.
12.
如图
分别延长
,
交
于点
和点
.
平分
,
于点
,
,.
又
,
.
,
同理可得:,
为
的中位线.
.
13.
(1)
、
分别是
、
的中点,
,,
、
分别是
、
的中点,
,,
,,
四边形
是平行四边形;
??????(2)
和
互余,
,
,
为
的中点,,
.
由(1)有四边形
是平行四边形,
.
14.
(1)
延长
,
交于点
,
因为
为
的中点,
所以
.
因为
,,
所以
.
所以
,.
因为
,
所以
垂直平分
.
所以
.
(或者延长
,).
??????(2)
过点
作
的平行线交
的延长线于点
,过
作
的垂线,垂足为
,连接
.
易知
,.
所以
,.
因为
,
所以
.
所以
.
所以
.
所以
.
所以
为等腰直角三角形.
所以
.
所以
.
所以
.
因为在
中,,,.
所以
.
第1页(共9
页)
一、选择题(共5小题;共25分)
1.
如图,在四边形
中,
是对角线
的中点,,
分别是
,
的中点,,,则
的度数是
A.
B.
C.
D.
2.
已知四边形ABCD中,,
分别是
,
上的点,,
分别是
,
的中点,当点
在
上从
向
移动而点
不动时,那么下列结论成立的是
A.
线段
的长逐渐增大
B.
线段
的长逐渐减小
C.
线段
的长不变
D.
线段
的长与点
的位置有关
3.
如图,
中,,,
、
分别是其角平分线和中线,过点
作
于
,交
于
,连接
,则线段
的长为
A.
B.
C.
D.
4.
如图,
的周长为
,点
,
都在边
上,
的平分线垂直于
,垂足为
,
的平分线垂直于
,垂足为
.若
,则
的长为
A.
B.
C.
D.
5.
小明爸爸的风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如图所示的风筝,点
,,,
分别是四边形
各边的中点.其中阴影部分用甲布料,其余部分用乙布料(裁剪两种布料时,均不计余料).若生产这批风筝需要甲布料
匹,那么需要乙布料
A.
匹
B.
匹
C.
匹
D.
匹
二、填空题(共5小题;共25分)
6.
如图,,
两地被一座小山阻隔,为测量
,
两地之间的距离,在地面上选一点
,连接
,,分别取
,
的中点
,,测得
的长度为
米,则
,
两地之间的距离是
?
米.
7.
如图,在
中,,,,
分别是
,,
的中点,若
,则
?
.
8.
如图,平行四边形
的周长为
,对角线
,
相交于点
.点
是
的中点,,则
的周长为
?.
9.
如图,已知
的周长为
,连接
的三边中点构成第二个三角形,再连接第二个三角形的三边中点构成第三个三角形,依此类推,第
个三角形的周长是
?.
10.
已知:如图,,
分别是
的中线和角平分线,,,则
的长等于
?.
三、解答题(共4小题;共52分)
11.
如图,在
中,,
分别是
,
边的中点.
求证:,.
12.
如图,,
分别是
和
的平分线,
于点
,
于点
.
求证:.
13.
如图,点
是
内一点,连接
、
,并将
、
、
、
的中点
、
、
、
依次连接,得到四边形
.
(1)求证:四边形
是平行四边形;
(2)若
为
的中点,,
和
互余,求
的长度.
14.
(1)方法回顾
在学习三角形中位线时,为了探索三角形中位线的性质,思路如下:
第一步添加辅助线:如图
1,在
中,延长
(,
分别是
,
的中点)到点
,使得
,连接
;
第二步证明
,再证四边形
是平行四边形,从而得到
,.
(1)问题解决
如图
2,在正方形
中,
为
的中点,,
分别为
,
边上的点,若
,,,求
的长.
(2)拓展研究
如图
3,在四边形
中,,,
为
的中点,,
分别为
,
边上的点,若
,,,求
的长.
答案
1.
C
【解析】
在四边形
中,
是对角线
的中点,,
分别是
,
的中点,,
分别是
与
的中位线,,.,.故
是等腰三角形.,.
2.
C
【解析】连接
,由三角形中位线定理可知在
点的运动过程中,
一定等于
的一半.又由于
的长不变,所以可做出正确的判断.
3.
A
【解析】
是
的平分线,.又
,,..在
中,
为
的中点,
为
的中点,.
4.
C
【解析】由题意,,,.
,.
.
.
.
5.
C
【解析】先连接
,,利用三角形中位线定理.可得
,同理,可得
,,,四个式子相加,可得空白的四个三角形的面积和等于四边形
面积的一半,于是可得阴影部分面积等于空白部分四个三角形的面积,那么所需甲乙布料相等,即乙也需
匹.
6.
7.
8.
【解析】提示:由题意可知
的周长
.
9.
【解析】由三角形的中位线定理,第二个三角形的各边分别为
各边的一半,
第二个三角形的周长是
周长的
,即
,第三个三角形的周长是第二个三角形周长的
,即
,第四个三角形的周长是第三个三角形周长的
,即
以此类推,第
个三角形的周长是
.
10.
【解析】
如图,延长
至
,令
,连接
,过点
作
交
的延长线于点
,过点
作
交
于
.
是
的角平分线,,
,.
易得
,
,
又
,
四边形
为平行四边形.
,
,
.
在
中,
.
可证
,
,
,
,
.
11.
延长
到点
使
,连接
.
在
中,
,
,
,,
又
,
,
四边形
为平行四边形.
,,即
,.
12.
如图
分别延长
,
交
于点
和点
.
平分
,
于点
,
,.
又
,
.
,
同理可得:,
为
的中位线.
.
13.
(1)
、
分别是
、
的中点,
,,
、
分别是
、
的中点,
,,
,,
四边形
是平行四边形;
??????(2)
和
互余,
,
,
为
的中点,,
.
由(1)有四边形
是平行四边形,
.
14.
(1)
延长
,
交于点
,
因为
为
的中点,
所以
.
因为
,,
所以
.
所以
,.
因为
,
所以
垂直平分
.
所以
.
(或者延长
,).
??????(2)
过点
作
的平行线交
的延长线于点
,过
作
的垂线,垂足为
,连接
.
易知
,.
所以
,.
因为
,
所以
.
所以
.
所以
.
所以
.
所以
为等腰直角三角形.
所以
.
所以
.
所以
.
因为在
中,,,.
所以
.
第1页(共9
页)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
