2021年人教版七年级数学上册暑假预习练习(Word版含解答): 4.1 几何图形
文档属性
| 名称 | 2021年人教版七年级数学上册暑假预习练习(Word版含解答): 4.1 几何图形 |  | |
| 格式 | docx | ||
| 文件大小 | 320.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-22 17:28:52 | ||
图片预览

文档简介
2021年人教版七年级数学上册暑假预习练习(Word版含解答): 4.1 几何图形
一、选择题
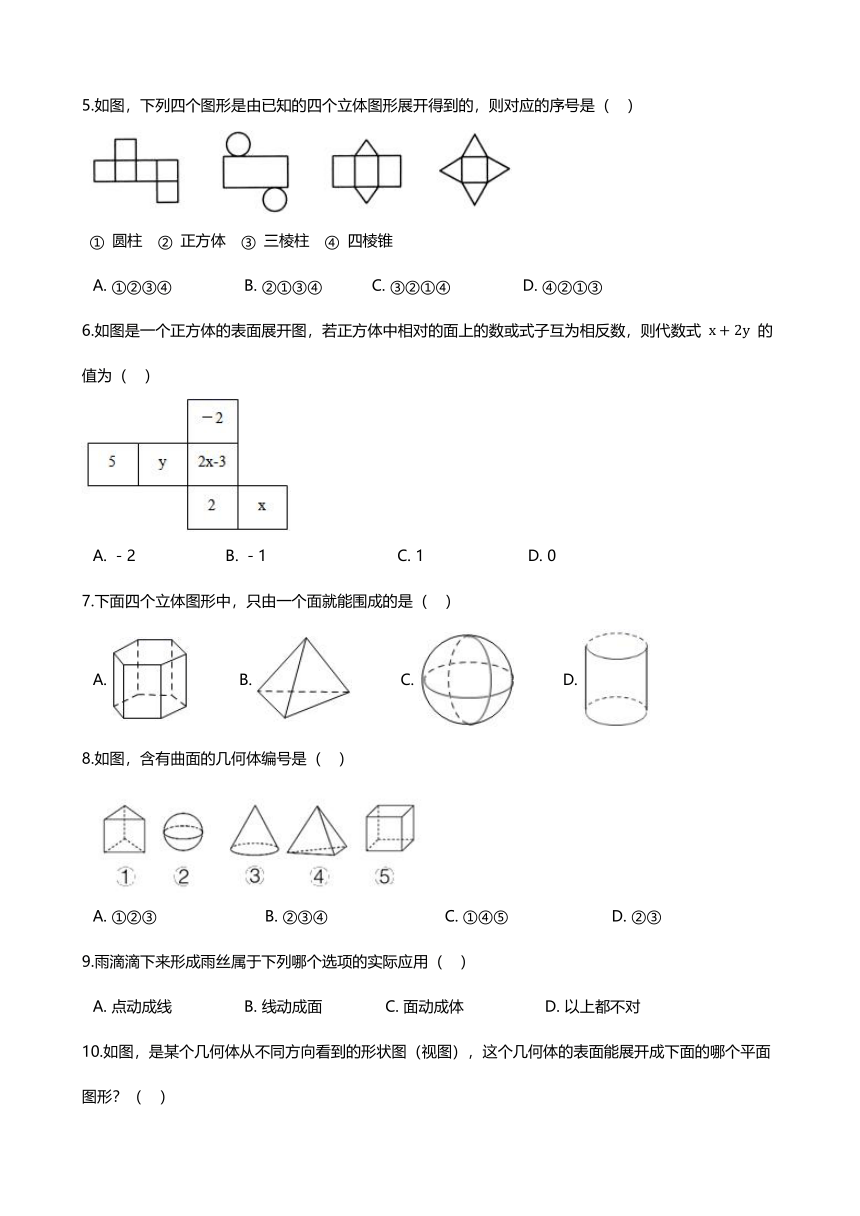
1.在下图的四个立体图形中,从正面看是四边形的立体图形有(? )
A.?1个????????????????????????B.?2个????????????????????????????C.?3个???????????????????????D.?4个
2.按如图所示图形中的虚线折叠可以围成一个棱柱的是(?? )
A.??????????????B.?
C.????????????D.?
3.下列图形绕虚线旋转一周,便能形成圆锥体的是( )
A.??????????????????????B.?????????????????????C.?????????????????????D.?
4.如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“迎”字一面的相对面上的字是(?? )
A.?百?????????????????????????????B.?党???????????????????????C.?年??????????????????D.?喜
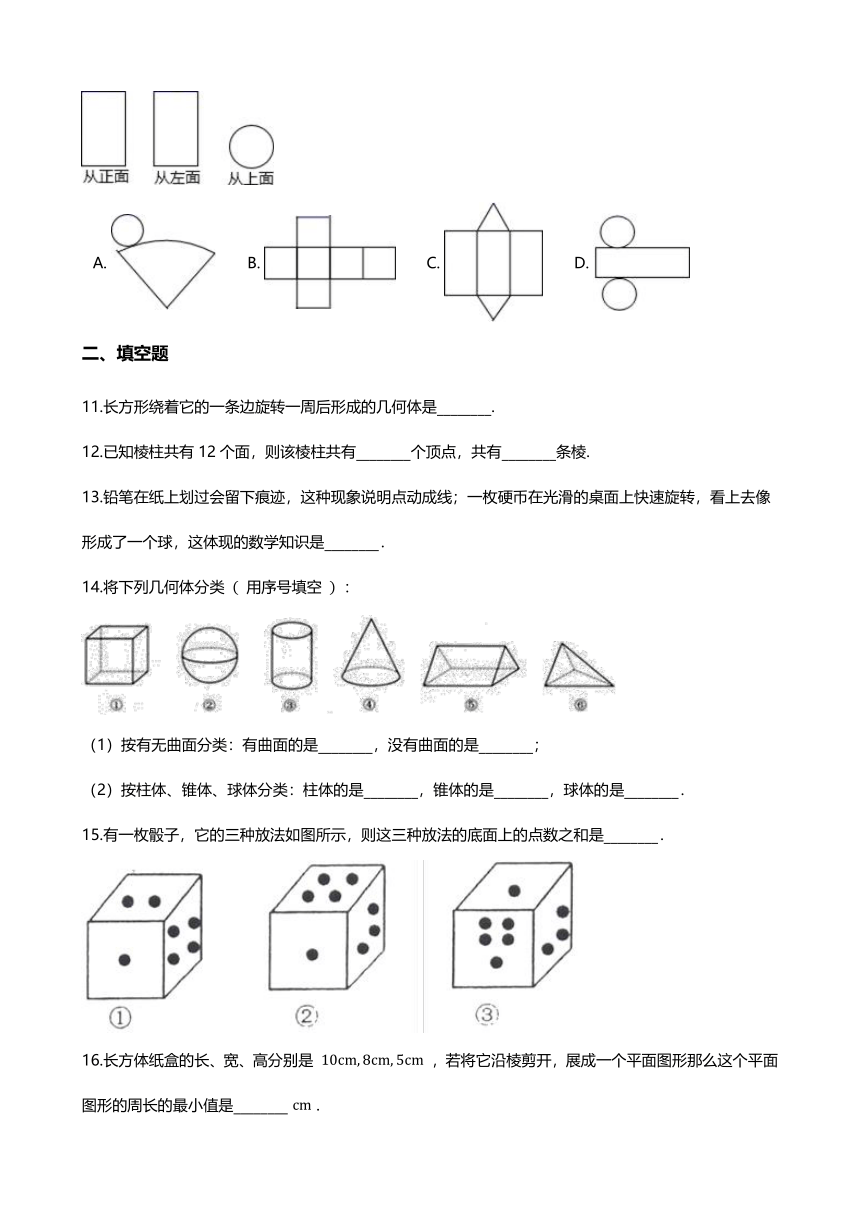
5.如图,下列四个图形是由已知的四个立体图形展开得到的,则对应的序号是(?? )
① 圆柱 ② 正方体 ③ 三棱柱 ④ 四棱锥
A.?①②③④????????????????B.?②①③④???????????C.?③②①④????????????????D.?④②①③
6.如图是一个正方体的表面展开图,若正方体中相对的面上的数或式子互为相反数,则代数式 x+2y 的值为(?? )
A.?-2????????????????????B.?-1?????????????????????????????C.?1???????????????????????D.?0
7.下面四个立体图形中,只由一个面就能围成的是(?? )
A.????????????B.????????????C.????????????D.?
8.如图,含有曲面的几何体编号是(?? )
A.?①②③????????????????????????B.?②③④??????????????????????????C.?①④⑤???????????????????????D.?②③
9.雨滴滴下来形成雨丝属于下列哪个选项的实际应用(?? )
A.?点动成线????????????????B.?线动成面??????????????C.?面动成体??????????????????D.?以上都不对
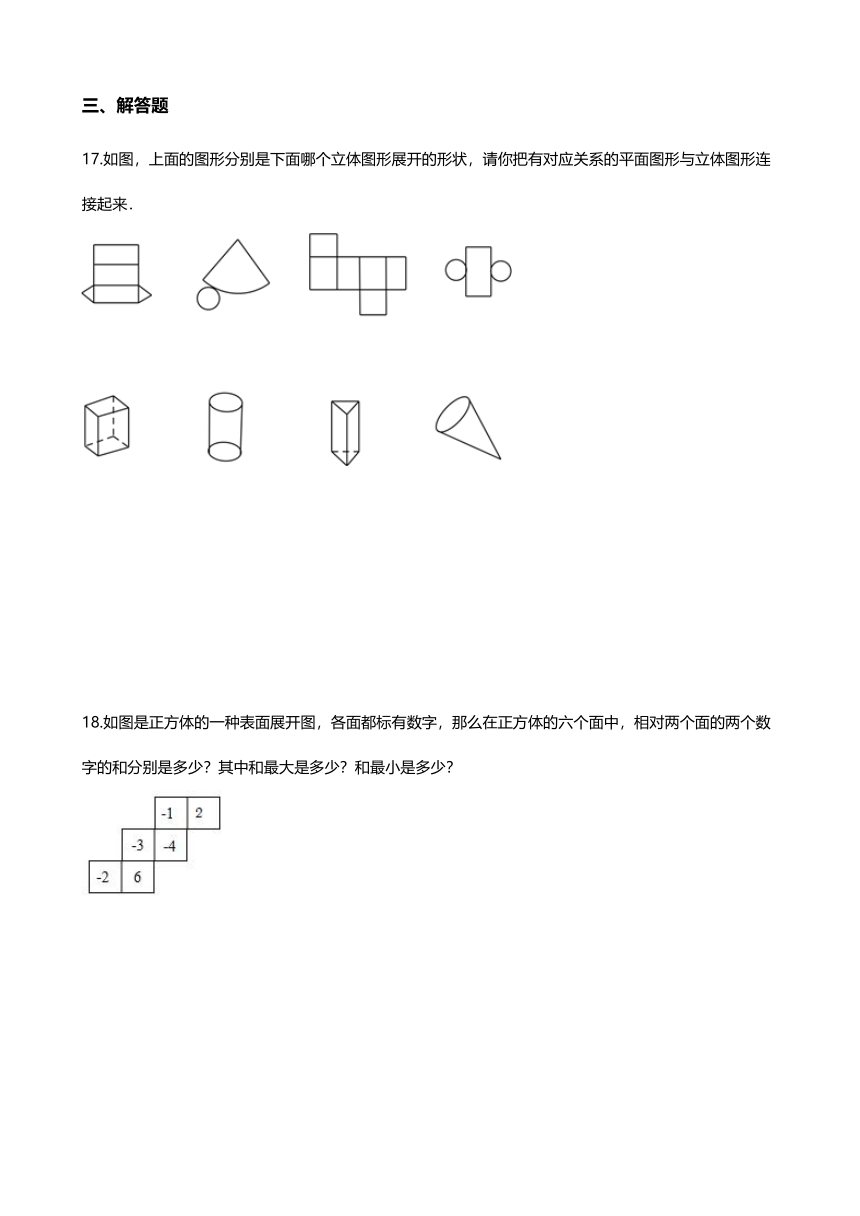
10.如图,是某个几何体从不同方向看到的形状图(视图),这个几何体的表面能展开成下面的哪个平面图形?(?? )
A.????????B.????????C.????????D.?
二、填空题
11.长方形绕着它的一条边旋转一周后形成的几何体是________.
12.已知棱柱共有12个面,则该棱柱共有________个顶点,共有________条棱.
13.铅笔在纸上划过会留下痕迹,这种现象说明点动成线;一枚硬币在光滑的桌面上快速旋转,看上去像形成了一个球,这体现的数学知识是________.
14.将下列几何体分类 ( 用序号填空 ) :
?
(1)按有无曲面分类:有曲面的是________,没有曲面的是________;
(2)按柱体、锥体、球体分类:柱体的是________,锥体的是________,球体的是________.
15.有一枚骰子,它的三种放法如图所示,则这三种放法的底面上的点数之和是________.
16.长方体纸盒的长、宽、高分别是 10cm,8cm,5cm ,若将它沿棱剪开,展成一个平面图形那么这个平面图形的周长的最小值是________ cm .
三、解答题
17.如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.
18.如图是正方体的一种表面展开图,各面都标有数字,那么在正方体的六个面中,相对两个面的两个数字的和分别是多少?其中和最大是多少?和最小是多少?
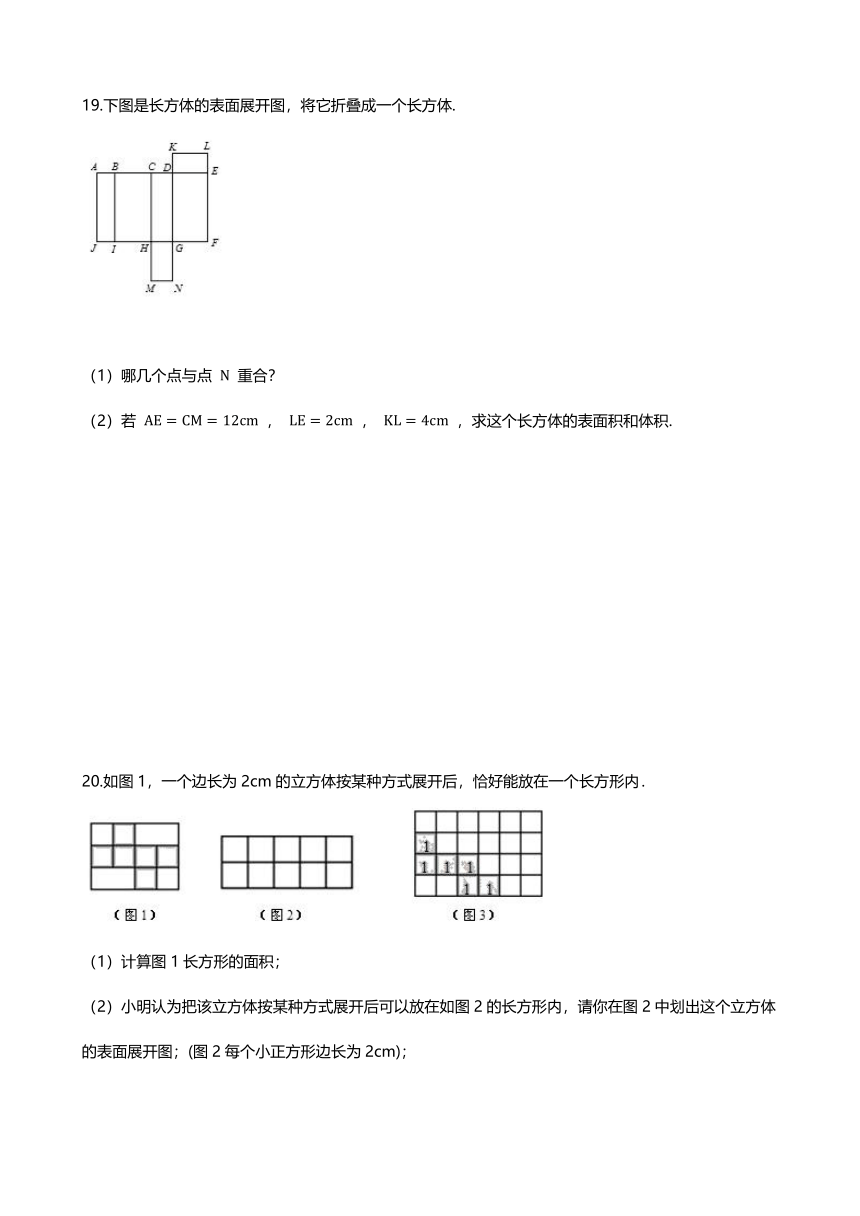
19.下图是长方体的表面展开图,将它折叠成一个长方体.
?
(1)哪几个点与点 N 重合?
(2)若 AE=CM=12cm , LE=2cm , KL=4cm ,求这个长方体的表面积和体积.
20.如图1,一个边长为2cm的立方体按某种方式展开后,恰好能放在一个长方形内.
(1)计算图1长方形的面积;
(2)小明认为把该立方体按某种方式展开后可以放在如图2的长方形内,请你在图2中划出这个立方体的表面展开图;(图2每个小正方形边长为2cm);
(3)如图3,在长12cm、宽8cm的长方形内已经画出该立方体的一种表面展开图(各个面都用数字“1”表示),请你在剩下部分再画出2个该立方体的表面展开图,把一个立方体的每一个面标记为“2”,另一个立方体的每一个面标记为“3”.
21.如图是一个正方体纸盒的表面展开图,纸盒中相对两个面上的数互为倒数.
(1)填空: a= ________, b= ________;
(2)先化简,再求值: -3(ab-a2)-[2b2-(5ab-a2)-2ab] .
22.如图1,在平整的地面上,用 8 个棱长都为 1cm 的小正方体堆成一个几何体.
(1)请在图2中画出从正面、左面和上面看到的这个几何体的形状图;
(2)如果现在你还有一些大小相同的小正方体,要求保持从上面和左面看到的形状图都不变,最多可以再添加多少个小正方体;
(3)求图1中 8 个小正方体搭成的几何体的表面积(包括与地面接触的部分).
?
23.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.
请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
________
长方体
8
6
12
正八面体
________
8
12
正十二面体
20
12
30
(2)你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是________.
(3)一个多面体的面数与顶点数相同,且有12条棱,则这个多面体的面数是________.
答案
一、选择题
1.解:正方体的主视图是四边形;
球的主视图是圆;
圆柱的主视图是四边形;
圆锥的主视图是等腰三角形;
从正面看是四边形的立体图形有两个.
故答案为:B.
2.棱柱的两个底面展开后在侧面展开图相对的两边上,所以A、D选项错误;
当底面为三角形时,则棱柱有三个侧面,所以B选项错误,C选项正确.
故答案为:C.
3.解:A、旋转一周得到的是球体,故不符合题意;
B、旋转一周是圆柱,故不符合题意;
C、旋转一周是圆锥体,故符合题意;
D、旋转一周不是圆锥体,故不符合题意.
故答案为:C.
4.解:正方体的表面展开图,相对的面之间一定相隔一个正方体,“迎”与“党”是相对面,“建”与“百”是相对面,“喜”与“年”是相对面.
故答案为:B.
5.解:观察图形,由立体图形及其表面展开图的特点可知相应的立体图形顺次是正方体、圆柱、三棱柱、四棱锥.
故答案为:B.
6.解: ∵ 正方体的表面展开图,相对的面之间一定相隔一个正方形,
∴5 与 2x-3 是相对面,
y与x是相对面,
2 与 -2 是相对面
根据题意得,
2x-3=-5 , y=-x ∴2x=-2 ∴x=-1 ∴y=-x=1
当 x=-1,y=1 时,x+2y=-1+2×1=-1+2=1
故答案为:C.
7.解:A、六棱柱是由8个面构成的,此项不符合题意;
B、四面体是由4个面构成的,此项不符合题意;
C、球是由一个曲面组成,此项符题意
D、圆柱体是由两个底面和一个侧面组成,
故答案为:C.
8.解:根据题意得:只要有一个面是曲面且是立体图形都符合题意,故含有曲面的是圆锥、球.
故答案为:D.
9.解:雨滴滴下来形成雨丝属于点动成线,
故答案为:A.
10.解:根据三视图可判断这个几何体是圆柱;D选项平面图一个长方形和两个圆折叠后,能围成的几何体是圆柱.A选项平面图折叠后是一个圆锥;B选项平面图折叠后是一个正方体;C选项平面图折叠后是一个三棱柱.
故答案为:D.
二、填空题
11.解:长方形绕着它的一条边旋转一周后形成的几何体是圆柱体.
故答案为:圆柱体.
12.解:∵棱柱有12个面,上底面和下底面是2个,
∴侧面有10个面,
∴它的上底面和下底面都是十边形,
∴它有20个顶点,
竖着的棱有10条,上底面有10条棱,下底面有10条棱,
∴一共有30条棱.
故答案是:20,30.
13.解:铅笔在纸上划过会留下痕迹,这种现象说明点动成线;一枚硬币在光滑的桌面上快速旋转,看上去像形成了一个球,这体现的数学知识是面动成体.
故答案为:面动成体.
14.(1)按有无曲面分类:有曲面的是②③④,没有曲面的是①⑤⑥,
故答案为:②③④;①⑤⑥;(2)按柱体,锥体,球体分类:柱体的是①③⑤,锥体的是④⑥,球体的是②.
故答案为:①③⑤;④⑥;②.
15.解:由题意得面“1”与面“6”相对,面“4”与面“5”相对,“2”与面“3”相对.
所以这三种放法的底面上的点数分别是3,5,6,其和是14.
故答案为:14.
16.解:根据题意,长方体展开图所得的平面图形周长最小的情况:如下图,
∴最小周长为: 5×8+8×4+10×2=92 cm;
故答案为:92.
三、解答题
17. 解:∵三个长方形和两个三角形如图摆放是三棱柱的展开图,一个扇形和一个圆是圆锥如图摆放的展开图,六个长方形如图摆放是长方体的展开图,一个长方形和两个圆如图摆放是圆柱的展开图,
∴连接如图:
18. 解:因为图形是正方体的表面展开图
所以“-3”与“2”是向对面,和是 -3+2=-1
“-1”与“6”是向对面,和是 -1+6=5
“-2”与“-4”是向对面,和是 -2+(-4)=-6
其中和最大是5,和最小是-6.
19. (1)解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;
(2)解:由 AE=CM=12cm , KL=4cm ,可得CH=CM-LK=12-4=8cm,
长方体的表面积;2×(8×4+2×4+2×8)=112cm2;
体积:4×8×2=64cm3.
20. (1)立方体的棱长为2cm,图1长方形的面积为4×2×3×2=48平方厘米。
(2)展开图:?
(3)
21. (1)-1;-13
(2)解: -3(ab-a2)-[2b2-(5ab-a2)-2ab]
=-3ab+3a2-2b2+5ab-a2+2ab
=2a2+4ab-2b2
将 a=-1,b=-13, 代入,
原式 =2×(-1)2+4×(-1)×(-13)-2×(-13)2
=2+43-29
=289 .
解:(1)由长方体纸盒的平面展开图知, a 与-1、 b 与-3、 c 与2是相对的两个面上的数字或字母,
因为相对的两个面上的数互为倒数,
所以 a=-1,b=-13,c=12 .
故答案为:-1, -13 .
22. (1)解:根据立体图形,三视图作图分别如下:
(2)解:结合题意,小正方体可以加在从前往后第二排第二层的空缺处,最多可以再添加1个正方体.故答案为1.
(3)解:根据小正方体的棱长都为 1cm ,可知每个面的小正方形面积为 1cm2 ,从对立体图形的观察可知,在外的面一共由32个,则几何体的表面积是 32cm2 .
23.(1)6;6
(2)V+F-E=2
(3)7
解:(1)观察图形,四面体的棱数为6;正八面体的顶点数为6;
多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
6
长方体
8
6
12
正八面体
6
8
12
正十二面体
20
12
30
;(2)观察表格可以看出:顶点数+面数-棱数=2,关系式为:V+F-E=2;
;(3)由题意得:F+F-12=2,解得F=7.
故答案为:(1)6,6;(2)V+F-E=2;(3)7.
一、选择题
1.在下图的四个立体图形中,从正面看是四边形的立体图形有(? )
A.?1个????????????????????????B.?2个????????????????????????????C.?3个???????????????????????D.?4个
2.按如图所示图形中的虚线折叠可以围成一个棱柱的是(?? )
A.??????????????B.?
C.????????????D.?
3.下列图形绕虚线旋转一周,便能形成圆锥体的是( )
A.??????????????????????B.?????????????????????C.?????????????????????D.?
4.如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“迎”字一面的相对面上的字是(?? )
A.?百?????????????????????????????B.?党???????????????????????C.?年??????????????????D.?喜
5.如图,下列四个图形是由已知的四个立体图形展开得到的,则对应的序号是(?? )
① 圆柱 ② 正方体 ③ 三棱柱 ④ 四棱锥
A.?①②③④????????????????B.?②①③④???????????C.?③②①④????????????????D.?④②①③
6.如图是一个正方体的表面展开图,若正方体中相对的面上的数或式子互为相反数,则代数式 x+2y 的值为(?? )
A.?-2????????????????????B.?-1?????????????????????????????C.?1???????????????????????D.?0
7.下面四个立体图形中,只由一个面就能围成的是(?? )
A.????????????B.????????????C.????????????D.?
8.如图,含有曲面的几何体编号是(?? )
A.?①②③????????????????????????B.?②③④??????????????????????????C.?①④⑤???????????????????????D.?②③
9.雨滴滴下来形成雨丝属于下列哪个选项的实际应用(?? )
A.?点动成线????????????????B.?线动成面??????????????C.?面动成体??????????????????D.?以上都不对
10.如图,是某个几何体从不同方向看到的形状图(视图),这个几何体的表面能展开成下面的哪个平面图形?(?? )
A.????????B.????????C.????????D.?
二、填空题
11.长方形绕着它的一条边旋转一周后形成的几何体是________.
12.已知棱柱共有12个面,则该棱柱共有________个顶点,共有________条棱.
13.铅笔在纸上划过会留下痕迹,这种现象说明点动成线;一枚硬币在光滑的桌面上快速旋转,看上去像形成了一个球,这体现的数学知识是________.
14.将下列几何体分类 ( 用序号填空 ) :
?
(1)按有无曲面分类:有曲面的是________,没有曲面的是________;
(2)按柱体、锥体、球体分类:柱体的是________,锥体的是________,球体的是________.
15.有一枚骰子,它的三种放法如图所示,则这三种放法的底面上的点数之和是________.
16.长方体纸盒的长、宽、高分别是 10cm,8cm,5cm ,若将它沿棱剪开,展成一个平面图形那么这个平面图形的周长的最小值是________ cm .
三、解答题
17.如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.
18.如图是正方体的一种表面展开图,各面都标有数字,那么在正方体的六个面中,相对两个面的两个数字的和分别是多少?其中和最大是多少?和最小是多少?
19.下图是长方体的表面展开图,将它折叠成一个长方体.
?
(1)哪几个点与点 N 重合?
(2)若 AE=CM=12cm , LE=2cm , KL=4cm ,求这个长方体的表面积和体积.
20.如图1,一个边长为2cm的立方体按某种方式展开后,恰好能放在一个长方形内.
(1)计算图1长方形的面积;
(2)小明认为把该立方体按某种方式展开后可以放在如图2的长方形内,请你在图2中划出这个立方体的表面展开图;(图2每个小正方形边长为2cm);
(3)如图3,在长12cm、宽8cm的长方形内已经画出该立方体的一种表面展开图(各个面都用数字“1”表示),请你在剩下部分再画出2个该立方体的表面展开图,把一个立方体的每一个面标记为“2”,另一个立方体的每一个面标记为“3”.
21.如图是一个正方体纸盒的表面展开图,纸盒中相对两个面上的数互为倒数.
(1)填空: a= ________, b= ________;
(2)先化简,再求值: -3(ab-a2)-[2b2-(5ab-a2)-2ab] .
22.如图1,在平整的地面上,用 8 个棱长都为 1cm 的小正方体堆成一个几何体.
(1)请在图2中画出从正面、左面和上面看到的这个几何体的形状图;
(2)如果现在你还有一些大小相同的小正方体,要求保持从上面和左面看到的形状图都不变,最多可以再添加多少个小正方体;
(3)求图1中 8 个小正方体搭成的几何体的表面积(包括与地面接触的部分).
?
23.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.
请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
________
长方体
8
6
12
正八面体
________
8
12
正十二面体
20
12
30
(2)你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是________.
(3)一个多面体的面数与顶点数相同,且有12条棱,则这个多面体的面数是________.
答案
一、选择题
1.解:正方体的主视图是四边形;
球的主视图是圆;
圆柱的主视图是四边形;
圆锥的主视图是等腰三角形;
从正面看是四边形的立体图形有两个.
故答案为:B.
2.棱柱的两个底面展开后在侧面展开图相对的两边上,所以A、D选项错误;
当底面为三角形时,则棱柱有三个侧面,所以B选项错误,C选项正确.
故答案为:C.
3.解:A、旋转一周得到的是球体,故不符合题意;
B、旋转一周是圆柱,故不符合题意;
C、旋转一周是圆锥体,故符合题意;
D、旋转一周不是圆锥体,故不符合题意.
故答案为:C.
4.解:正方体的表面展开图,相对的面之间一定相隔一个正方体,“迎”与“党”是相对面,“建”与“百”是相对面,“喜”与“年”是相对面.
故答案为:B.
5.解:观察图形,由立体图形及其表面展开图的特点可知相应的立体图形顺次是正方体、圆柱、三棱柱、四棱锥.
故答案为:B.
6.解: ∵ 正方体的表面展开图,相对的面之间一定相隔一个正方形,
∴5 与 2x-3 是相对面,
y与x是相对面,
2 与 -2 是相对面
根据题意得,
2x-3=-5 , y=-x ∴2x=-2 ∴x=-1 ∴y=-x=1
当 x=-1,y=1 时,x+2y=-1+2×1=-1+2=1
故答案为:C.
7.解:A、六棱柱是由8个面构成的,此项不符合题意;
B、四面体是由4个面构成的,此项不符合题意;
C、球是由一个曲面组成,此项符题意
D、圆柱体是由两个底面和一个侧面组成,
故答案为:C.
8.解:根据题意得:只要有一个面是曲面且是立体图形都符合题意,故含有曲面的是圆锥、球.
故答案为:D.
9.解:雨滴滴下来形成雨丝属于点动成线,
故答案为:A.
10.解:根据三视图可判断这个几何体是圆柱;D选项平面图一个长方形和两个圆折叠后,能围成的几何体是圆柱.A选项平面图折叠后是一个圆锥;B选项平面图折叠后是一个正方体;C选项平面图折叠后是一个三棱柱.
故答案为:D.
二、填空题
11.解:长方形绕着它的一条边旋转一周后形成的几何体是圆柱体.
故答案为:圆柱体.
12.解:∵棱柱有12个面,上底面和下底面是2个,
∴侧面有10个面,
∴它的上底面和下底面都是十边形,
∴它有20个顶点,
竖着的棱有10条,上底面有10条棱,下底面有10条棱,
∴一共有30条棱.
故答案是:20,30.
13.解:铅笔在纸上划过会留下痕迹,这种现象说明点动成线;一枚硬币在光滑的桌面上快速旋转,看上去像形成了一个球,这体现的数学知识是面动成体.
故答案为:面动成体.
14.(1)按有无曲面分类:有曲面的是②③④,没有曲面的是①⑤⑥,
故答案为:②③④;①⑤⑥;(2)按柱体,锥体,球体分类:柱体的是①③⑤,锥体的是④⑥,球体的是②.
故答案为:①③⑤;④⑥;②.
15.解:由题意得面“1”与面“6”相对,面“4”与面“5”相对,“2”与面“3”相对.
所以这三种放法的底面上的点数分别是3,5,6,其和是14.
故答案为:14.
16.解:根据题意,长方体展开图所得的平面图形周长最小的情况:如下图,
∴最小周长为: 5×8+8×4+10×2=92 cm;
故答案为:92.
三、解答题
17. 解:∵三个长方形和两个三角形如图摆放是三棱柱的展开图,一个扇形和一个圆是圆锥如图摆放的展开图,六个长方形如图摆放是长方体的展开图,一个长方形和两个圆如图摆放是圆柱的展开图,
∴连接如图:
18. 解:因为图形是正方体的表面展开图
所以“-3”与“2”是向对面,和是 -3+2=-1
“-1”与“6”是向对面,和是 -1+6=5
“-2”与“-4”是向对面,和是 -2+(-4)=-6
其中和最大是5,和最小是-6.
19. (1)解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;
(2)解:由 AE=CM=12cm , KL=4cm ,可得CH=CM-LK=12-4=8cm,
长方体的表面积;2×(8×4+2×4+2×8)=112cm2;
体积:4×8×2=64cm3.
20. (1)立方体的棱长为2cm,图1长方形的面积为4×2×3×2=48平方厘米。
(2)展开图:?
(3)
21. (1)-1;-13
(2)解: -3(ab-a2)-[2b2-(5ab-a2)-2ab]
=-3ab+3a2-2b2+5ab-a2+2ab
=2a2+4ab-2b2
将 a=-1,b=-13, 代入,
原式 =2×(-1)2+4×(-1)×(-13)-2×(-13)2
=2+43-29
=289 .
解:(1)由长方体纸盒的平面展开图知, a 与-1、 b 与-3、 c 与2是相对的两个面上的数字或字母,
因为相对的两个面上的数互为倒数,
所以 a=-1,b=-13,c=12 .
故答案为:-1, -13 .
22. (1)解:根据立体图形,三视图作图分别如下:
(2)解:结合题意,小正方体可以加在从前往后第二排第二层的空缺处,最多可以再添加1个正方体.故答案为1.
(3)解:根据小正方体的棱长都为 1cm ,可知每个面的小正方形面积为 1cm2 ,从对立体图形的观察可知,在外的面一共由32个,则几何体的表面积是 32cm2 .
23.(1)6;6
(2)V+F-E=2
(3)7
解:(1)观察图形,四面体的棱数为6;正八面体的顶点数为6;
多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
6
长方体
8
6
12
正八面体
6
8
12
正十二面体
20
12
30
;(2)观察表格可以看出:顶点数+面数-棱数=2,关系式为:V+F-E=2;
;(3)由题意得:F+F-12=2,解得F=7.
故答案为:(1)6,6;(2)V+F-E=2;(3)7.
