江西省南昌市第八中学2020-2021学年下学期高一数学必修三期末课后复习试题 Word版含解析
文档属性
| 名称 | 江西省南昌市第八中学2020-2021学年下学期高一数学必修三期末课后复习试题 Word版含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 647.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-23 16:10:34 | ||
图片预览




文档简介
必修三复习
一、单选题
1.某工厂利用随机数表对生产的50个零件进行抽样测试,先将50个零件进行编号,编号分别为01,02,…,50,从中抽取5个样本,下面提供随机数表的第1行到第2行:
若从表中第1行第9列开始向右依次读取数据,则得到的第4个样本编号是(
)
A.10
B.09
C.71
D.20
2.下面两个扇形统计图分别统计了某地2010年和2020年小学生参加课外兴趣班的情况,已知2020年当地小学生参加课外兴趣班的总人数是2010年当地小学生参加课外兴趣班的总人数的4倍,下面说法不正确的是(
)
A.2020年参加音乐兴趣班的小学生人数是2010年参加音乐兴趣班的小学生人数的4倍
B.这10年间,参加编程兴趣班的小学生人数变化最大
C.2020年参加美术兴趣班的小学生人数少于2010年参加美术兴趣班的小学生人数
D.相对于2010年,2020年参加不同课外兴趣班的小学生人数更平均
3.在一次科普知识竞赛中共有名同学参赛,经过评判,这名参赛者的得分都在之间,其得分的频率分布直方图如图,则下列结论错误的是(
)
A.可求得
B.这名参赛者得分的中位数为
C.得分在之间的频率为
D.得分在之间的共有人
4.某大学共有名学生,为了了解学生课外图书阅读量情况,该校随机地从全校学生中抽取名,统计他们每年阅读的书籍数量,由此来估计全体学生当年的阅读书籍数量的情况,下列估计中正确的是(注:同一组数据用该组区间的中点值作为代表)(
)
A.中位数为
B.众数为
C.平均数为
D.该校读书不低于本的人数约为人
5.已知某种商品的广告费支出x(单位:万元)与销售额y(单位:万元)之间有如下对应数据:
x
2
4
5
6
8
y
30
40
50
m
60
根据表中的全部数据,用最小二乘法得出y与x的线性回归方程为=6.5x+17.5,则表中m的值为(
)
A.45
B.50
C.55
D.70
6.已知变量x,y之间的线性回归方程为,且变量x,y之间的一组相关数据如下表所示,则下列说法错误的是(
)
x
6
8
10
12
y
6
m
3
2
A.变量x,y之间呈负相关关系
B.可以预测,当时,
C.
D.该回归直线必过点
7.下列给出的赋值语句中正确的是(
).
A.
B.
C.
D.
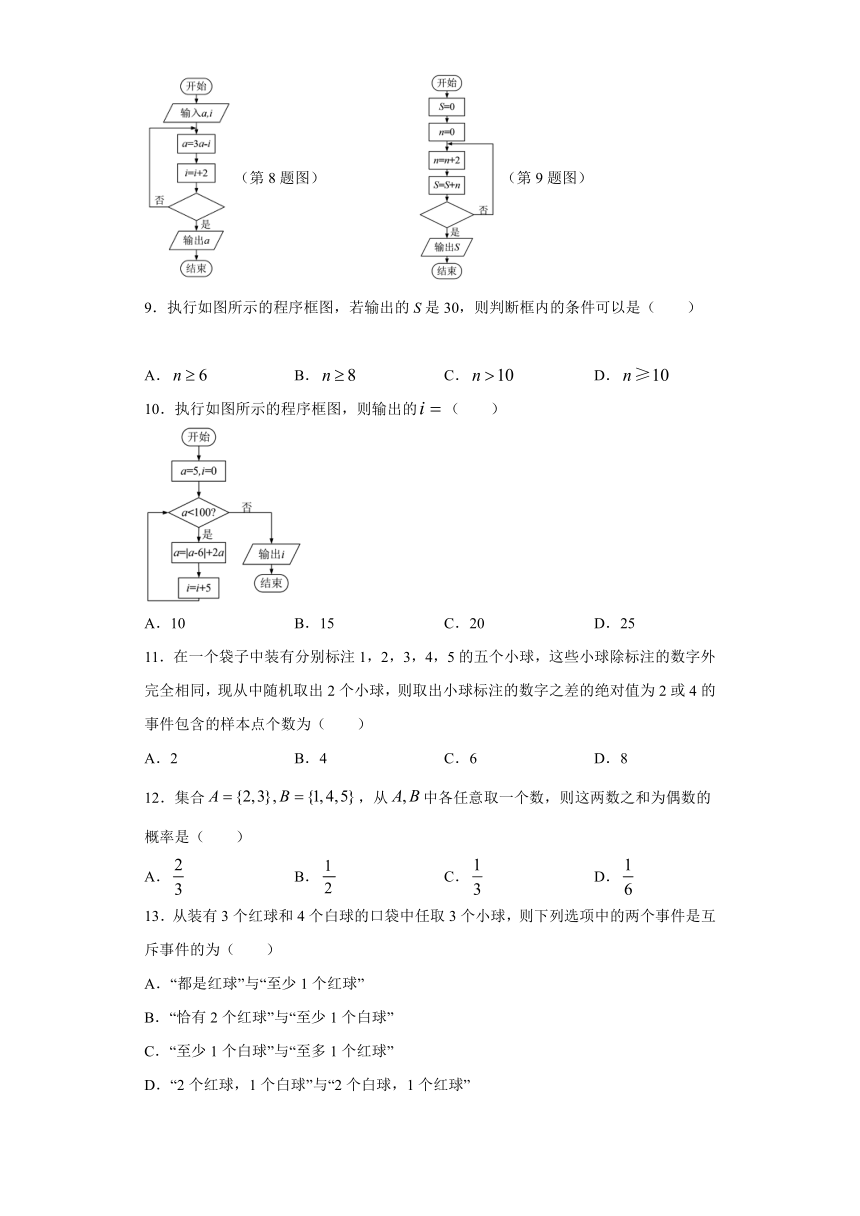
8.执行如图的程序框图,若输入,,输出,则在空白框中可以填入(
)
A.
B.
C.
D.
(第8题图)
(第9题图)
9.执行如图所示的程序框图,若输出的S是30,则判断框内的条件可以是(
)
A.
B.
C.
D.
10.执行如图所示的程序框图,则输出的(
)
A.10
B.15
C.20
D.25
11.在一个袋子中装有分别标注1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同,现从中随机取出2个小球,则取出小球标注的数字之差的绝对值为2或4的事件包含的样本点个数为(
)
A.2
B.4
C.6
D.8
12.集合,从中各任意取一个数,则这两数之和为偶数的概率是(
)
A.
B.
C.
D.
13.从装有3个红球和4个白球的口袋中任取3个小球,则下列选项中的两个事件是互斥事件的为(
)
A.“都是红球”与“至少1个红球”
B.“恰有2个红球”与“至少1个白球”
C.“至少1个白球”与“至多1个红球”
D.“2个红球,1个白球”与“2个白球,1个红球”
二、填空题
14.某单位有名职工,现采用系统抽样抽取人做问卷调查,将人按,,…,随机编号,则抽取的人中,编号落入区间的人数为___________.
15.某新学校高一、高二、高三共有学生1900名,为了了解同学们对学校关于对手机管理的意见,计划采用分层抽样的方法,从这1900名学生中抽取一个样本容量为38的样本,若从高一、高二、高三抽取的人数恰好组成一个以为公比的等比数列,则此学校高一年级的学生人数为______人.
16.已知一组数据按从小到大的顺序排列,得到-1,0,4,x,7,14,中位数为5,则这组数据的平均数为________.
17.某企业一种商品的产量与单位成本数据如下表:
产量(万件)
2
3
4
单位成本(元/件)
3
7
现根据表中所提供的数据,求得关于的线性回归直线方程为,则预测当时单位成本为每件______元.
18.下面是某算法的程序框图,则程序运行后输出的结果为___________.
19.设为三个随机事件,若与互斥,与对立,且,,则_____________.
20.甲、乙两人下棋,甲获胜的概率为0.3,两人下成和棋的概率为0.5,那么甲不输的概率是________.
21.若样本的平均数为10,其方差为2,则样本的平均数为____________,方差为____________.
22.5张彩票中仅有1张中奖彩票,5个人依次摸奖,则第二个人摸到中奖彩票的概率为________,第三个人摸到中奖彩票的概率为________.
三、解答题
23.某重点中学100位学生在市统考中的理科综合分数,以,
,
,
,
,
,
分组的频率分布直方图如图.
(1)求直方图中的值;
(2)求理科综合分数的众数和中位数;
(3)在理科综合分数为,
,
,
的四组学生中,用分层抽样的方法抽取11名学生,则理科综合分数在的学生中应抽取多少人?
24.某产品的广告费支出与销售额(单位:万元)之间有如下对应数据:
x
2
4
5
6
8
y
30
40
60
50
70
(1)求出回归直线方程;
(2)据此预测广告费支出万元,销售额是多少?
参考公式:
25.截止2020年11月23日,国务院扶贫办确定的全国832个贫困县已全部脱贫摘帽,各地为持续巩固脱贫攻坚成果,都建立了防止返贫检测和帮扶机制.为进一步推进乡村振兴,某市扶贫办在乡镇的3个脱贫村,乡镇的2个脱贫村以及乡镇的2个脱贫村中,随机抽取2个村庄进一步实施产业帮扶.
(1)求抽取的2个村庄来自同1个乡镇的概率;
(2)求抽取的2个村庄中至少有1个来自乡镇的概率.
26.甲、乙两个学习小组各有7名同学,在某次数学测试中,测试成绩的茎叶图如图所示.
(1)求甲组同学成绩的中位数和乙组同学成绩的众数;
(2)从这次测试成绩在90分以上的学生中,随机抽取1名学生,求抽到的这名学生来自甲组的概率.
27.某小区超市采取有力措施保障居民正常生活的物资供应.为做好日常生活必需的甲类物资的供应,超市对社区居民户每天对甲类物资的购买量进行了调查,得到了以下频率分布直方图(如图).
(1)估计该小区居民对甲类物资购买量的中位数;
(2)现将小区居民按照购买量分为两组,即购买量在(单位:)的居民为A组,购买量在(单位:)的居民为B组,采用分层抽样的方式从该小区中选出5户进行生活情况调查,再从这5户中随机选出3户,求选出的B组户数为2的概率.
必修三复习参考答案
1.B
【解析】从随机数表第1行的第9列数字开始由左向右每次连续读取2个数字,删除超出范围及重复的编号,符合条件的编号有14,05,11,09,
所以选出来的第4个个体的编号为09,故选:B
2.C
【解析】设2010年参加课外兴趣班的小学生总人数为,则2020年参加课外兴趣班的小学生总人数是.由统计图可知,2010年参加音乐兴趣班的小学生人数是,
2020年参加音乐兴趣班的小学生人数是,故A正确.
这10年间参加编程兴趣班的小学生人数变化量为,
这10年间参加语言表演的小学生人数变化量为,
这10年间参加音乐的小学生人数变化量为,
这10年间参加美术的小学生人数变化量为,
所以这10年间参加编程兴趣班的小学生人数变化量最大,故B正确.
2020年参加美术兴趣班的小学生人数为,2010年参加美术兴趣班的小学生人数为,,故C不正确,
根据扇形统计图中的比例分布,可知D正确.故选:C.
3.B
【解析】对于A选项,由于直方图的面积之和为,则,解得,A选项正确;
对于B选项,前两个矩形的面积之和为,前三个矩形的面积之和为,
设中位数为,则,则,解得,B选项错误;
对于C选项,得分在之间的频率为,C选项正确;
对于D选项,得分在之间的人数为,D选项正确.
故选:B.
4.C
【解析】A:由图知:中位数在,所以,解得,错误;
B:由图知:众数在,故众数为,错误;
C:平均数为,正确;
D:由图知:该校读书不低于本的频率之和为,所以该校读书不低于本的人数约为人.故选:C
5.D
【解析】由表可知,,
.
因为回归直线会经过平均数样本中心点,
所以=6.5×5+17.5,解得m=70.故选:D.
6.C
【解析】对于A,变量x,y之间的线性回归方程为,
而,所以变量x,y之间呈负相关关系,故选项A正确;
对于B,当时,,故选项B正确;
对于D,,所以,故D正确;
对于C,∵,∴,解得,故C不正确.
故选:C.
7.B
【解析】根据赋值语句的定义,变量=表达式,知ACD不是赋值语句,B满足.
故选:B.
8.A
【解析】运行程序框图,,;
,;
,;
…
,;
,,
因为输出,此时退出循环,所以空白框中可以填入.故选:A.
9.D
【解析】由程序框图,其执行结果如下:
1、:,执行循环体;
2、:,执行循环体;
3、:,执行循环体;
4、:,执行循环体;
5、:,跳出循环体,输出;
∴框内条件应为.故选:D.
10.C
【解析】第一次执行程序,;
第二次执行程序,;
第三次执行程序,;
第四次执行程序,,跳出循环输出,
故输出的.故选:C
11.B
【解析】从5个小球中任取2个,其中数字之差的绝对值为2或4的事件包含
(1,3),(1,5),(2,4),(3,5)4个样本点,故选:B.
12.B
【解析】从中任意取一个数,共有6种情形,两数和为偶数的情形有三种,.故选:B.
13.D
【解析】对于A选项:“至少1个红球”的事件中含有“都是红球”这一事件,即两个事件可以同时发生,A中的两个事件不互斥;
对于B选项:“恰有2个红球”和“至少1个白球”的事件中都含有“两红球,一白球”的事件,B中的两个事件不互斥;
对于C选项:“至少1个白球”与“至多1个红球”的事件中都含有“三白球”与“一红球,两白球”的两个事件,C中的两个事件不互斥;
对于D选项,3个球中“2个红球,1个白球”的事件与“2个白球,1个红球”的事件不可能同时发生,是互斥事件,所以两个事件是互斥事件的为D.故选:D
14.
【解析】由条件可知,分段间隔为:,
所以编号落入区间的人数为:
15.900
【解析】因为高一、高二、高三抽取的人数恰好组成一个以为公比的等比数列
设从高二年级抽取的学生人数为人,
则从高二、高三年级抽取的人数分别为.
由题意可得,所以.
设我校高一年级的学生人数为N,再根据,
求得.
16.5
【解析】∵-1,0,4,x,7,14的中位数为5,∴
,∴x=6.
∴这组数据的平均数是.
17.9
【解析】由所给数据可求得,,代入线性回归直线方程,得,解得,
所以线性回归直线方程,当时单位成本(元/件).
18.14
【解析】由程序框图知:第一次循环n=1,S=﹣1+1=0;
第二次循环n=2,S=0+1+2=3;
第三次循环n=3,S=3﹣1+3=5;
第四次循环n=4,S=5+1+4=10;
第五次循环n=5,S=10﹣1+5=14,
满足条件S>13,跳出循环,输出S的值为14.
19.
【解析】与对立,,
与互斥,.
20.0.8.
【解析】甲不输包括甲获胜和两人下和棋两个事件,这两个事件是互斥的。根据互斥事件的概率运算法则可知甲不输的概率是0.3+0.5=0.8.
21.11
2
【解析】对比两组数据我们发现后一组的每个数据都比前一组的每个数据多1,
所以平均数增加1,方差不变.故答案为:11;2
22.
【解析】记“第i个人抽中中奖彩票”为事件Ai
,第二个人摸到中奖彩票,指第一个人没有摸到,第二个人摸到,根据事件写出概率,第三个人摸到中奖彩票,指前两个人没有摸到,第三个人摸到,显然P(A1)=,而,.
故答案为:;
23.【解析】(1)因为,
解得,所以直方图中的值为.
(2)理科综合分数的众数是,
∵,
∴理科综合分数的中位数在内,设中位数为,
则,
解得,即中位数为.
(3)理科综合分数在的学生有(位),
同理可求理科综合分数为,
,
的用户分别有15位、10位、5位,
故抽取比为,
∴从理科综合分数在的学生中应抽取人.
24.【解析】(1),
,
,
,
,,
所以回归直线方程
(2)由回归直线方程可知,当广告费支出9万元时,
(万元),
答:销售额是76万元.
25.【解析】依题意,可设乡镇的3个脱贫村为,,,乡镇的2个脱贫村为,,乡镇的2个脱贫村为,.
从中随机抽取2个扶贫村的事件有,,,,,,,,,,,,,,,,,,,,共21种.
(1)抽取的2个村庄来自同1个乡镇的事件有,,,,,共5种,
所以抽取的2个村庄来自同1个乡镇的概率.
(2)抽取的2个村庄中至少有1个来自乡镇的事件有,,,,,,,,,,,,,,,共15种,
所以抽取的2个村庄中至少有1个来自乡镇的概率.
26.【解析】(1)甲组共有7名学生的成绩,其中位数为.
乙组成绩中,出现次数最多,故众数为.
(2)90分以上的学生共计5人,其中来自甲组有2人,
设为“随机抽取1名学生,求抽到的这名学生来自甲组”,则.
27.【解析】(1)由中位数两侧频率相等,而的频率为,的频率为,设中位数为,将分为和即有:
,解得;
(2)依据分层抽样,A组有2人为x,y,B组有3人为a,b,c,
从中任选3人,可能的情况为xya、xyb、xyc、xab
、xbc、xac、yab、ybc、yac、abc共10种情况,其中B组户数有2户的有xab、xbc、xac、yab、ybc、yac共6种,因此选出的B组户数为2的概率为.
一、单选题
1.某工厂利用随机数表对生产的50个零件进行抽样测试,先将50个零件进行编号,编号分别为01,02,…,50,从中抽取5个样本,下面提供随机数表的第1行到第2行:
若从表中第1行第9列开始向右依次读取数据,则得到的第4个样本编号是(
)
A.10
B.09
C.71
D.20
2.下面两个扇形统计图分别统计了某地2010年和2020年小学生参加课外兴趣班的情况,已知2020年当地小学生参加课外兴趣班的总人数是2010年当地小学生参加课外兴趣班的总人数的4倍,下面说法不正确的是(
)
A.2020年参加音乐兴趣班的小学生人数是2010年参加音乐兴趣班的小学生人数的4倍
B.这10年间,参加编程兴趣班的小学生人数变化最大
C.2020年参加美术兴趣班的小学生人数少于2010年参加美术兴趣班的小学生人数
D.相对于2010年,2020年参加不同课外兴趣班的小学生人数更平均
3.在一次科普知识竞赛中共有名同学参赛,经过评判,这名参赛者的得分都在之间,其得分的频率分布直方图如图,则下列结论错误的是(
)
A.可求得
B.这名参赛者得分的中位数为
C.得分在之间的频率为
D.得分在之间的共有人
4.某大学共有名学生,为了了解学生课外图书阅读量情况,该校随机地从全校学生中抽取名,统计他们每年阅读的书籍数量,由此来估计全体学生当年的阅读书籍数量的情况,下列估计中正确的是(注:同一组数据用该组区间的中点值作为代表)(
)
A.中位数为
B.众数为
C.平均数为
D.该校读书不低于本的人数约为人
5.已知某种商品的广告费支出x(单位:万元)与销售额y(单位:万元)之间有如下对应数据:
x
2
4
5
6
8
y
30
40
50
m
60
根据表中的全部数据,用最小二乘法得出y与x的线性回归方程为=6.5x+17.5,则表中m的值为(
)
A.45
B.50
C.55
D.70
6.已知变量x,y之间的线性回归方程为,且变量x,y之间的一组相关数据如下表所示,则下列说法错误的是(
)
x
6
8
10
12
y
6
m
3
2
A.变量x,y之间呈负相关关系
B.可以预测,当时,
C.
D.该回归直线必过点
7.下列给出的赋值语句中正确的是(
).
A.
B.
C.
D.
8.执行如图的程序框图,若输入,,输出,则在空白框中可以填入(
)
A.
B.
C.
D.
(第8题图)
(第9题图)
9.执行如图所示的程序框图,若输出的S是30,则判断框内的条件可以是(
)
A.
B.
C.
D.
10.执行如图所示的程序框图,则输出的(
)
A.10
B.15
C.20
D.25
11.在一个袋子中装有分别标注1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同,现从中随机取出2个小球,则取出小球标注的数字之差的绝对值为2或4的事件包含的样本点个数为(
)
A.2
B.4
C.6
D.8
12.集合,从中各任意取一个数,则这两数之和为偶数的概率是(
)
A.
B.
C.
D.
13.从装有3个红球和4个白球的口袋中任取3个小球,则下列选项中的两个事件是互斥事件的为(
)
A.“都是红球”与“至少1个红球”
B.“恰有2个红球”与“至少1个白球”
C.“至少1个白球”与“至多1个红球”
D.“2个红球,1个白球”与“2个白球,1个红球”
二、填空题
14.某单位有名职工,现采用系统抽样抽取人做问卷调查,将人按,,…,随机编号,则抽取的人中,编号落入区间的人数为___________.
15.某新学校高一、高二、高三共有学生1900名,为了了解同学们对学校关于对手机管理的意见,计划采用分层抽样的方法,从这1900名学生中抽取一个样本容量为38的样本,若从高一、高二、高三抽取的人数恰好组成一个以为公比的等比数列,则此学校高一年级的学生人数为______人.
16.已知一组数据按从小到大的顺序排列,得到-1,0,4,x,7,14,中位数为5,则这组数据的平均数为________.
17.某企业一种商品的产量与单位成本数据如下表:
产量(万件)
2
3
4
单位成本(元/件)
3
7
现根据表中所提供的数据,求得关于的线性回归直线方程为,则预测当时单位成本为每件______元.
18.下面是某算法的程序框图,则程序运行后输出的结果为___________.
19.设为三个随机事件,若与互斥,与对立,且,,则_____________.
20.甲、乙两人下棋,甲获胜的概率为0.3,两人下成和棋的概率为0.5,那么甲不输的概率是________.
21.若样本的平均数为10,其方差为2,则样本的平均数为____________,方差为____________.
22.5张彩票中仅有1张中奖彩票,5个人依次摸奖,则第二个人摸到中奖彩票的概率为________,第三个人摸到中奖彩票的概率为________.
三、解答题
23.某重点中学100位学生在市统考中的理科综合分数,以,
,
,
,
,
,
分组的频率分布直方图如图.
(1)求直方图中的值;
(2)求理科综合分数的众数和中位数;
(3)在理科综合分数为,
,
,
的四组学生中,用分层抽样的方法抽取11名学生,则理科综合分数在的学生中应抽取多少人?
24.某产品的广告费支出与销售额(单位:万元)之间有如下对应数据:
x
2
4
5
6
8
y
30
40
60
50
70
(1)求出回归直线方程;
(2)据此预测广告费支出万元,销售额是多少?
参考公式:
25.截止2020年11月23日,国务院扶贫办确定的全国832个贫困县已全部脱贫摘帽,各地为持续巩固脱贫攻坚成果,都建立了防止返贫检测和帮扶机制.为进一步推进乡村振兴,某市扶贫办在乡镇的3个脱贫村,乡镇的2个脱贫村以及乡镇的2个脱贫村中,随机抽取2个村庄进一步实施产业帮扶.
(1)求抽取的2个村庄来自同1个乡镇的概率;
(2)求抽取的2个村庄中至少有1个来自乡镇的概率.
26.甲、乙两个学习小组各有7名同学,在某次数学测试中,测试成绩的茎叶图如图所示.
(1)求甲组同学成绩的中位数和乙组同学成绩的众数;
(2)从这次测试成绩在90分以上的学生中,随机抽取1名学生,求抽到的这名学生来自甲组的概率.
27.某小区超市采取有力措施保障居民正常生活的物资供应.为做好日常生活必需的甲类物资的供应,超市对社区居民户每天对甲类物资的购买量进行了调查,得到了以下频率分布直方图(如图).
(1)估计该小区居民对甲类物资购买量的中位数;
(2)现将小区居民按照购买量分为两组,即购买量在(单位:)的居民为A组,购买量在(单位:)的居民为B组,采用分层抽样的方式从该小区中选出5户进行生活情况调查,再从这5户中随机选出3户,求选出的B组户数为2的概率.
必修三复习参考答案
1.B
【解析】从随机数表第1行的第9列数字开始由左向右每次连续读取2个数字,删除超出范围及重复的编号,符合条件的编号有14,05,11,09,
所以选出来的第4个个体的编号为09,故选:B
2.C
【解析】设2010年参加课外兴趣班的小学生总人数为,则2020年参加课外兴趣班的小学生总人数是.由统计图可知,2010年参加音乐兴趣班的小学生人数是,
2020年参加音乐兴趣班的小学生人数是,故A正确.
这10年间参加编程兴趣班的小学生人数变化量为,
这10年间参加语言表演的小学生人数变化量为,
这10年间参加音乐的小学生人数变化量为,
这10年间参加美术的小学生人数变化量为,
所以这10年间参加编程兴趣班的小学生人数变化量最大,故B正确.
2020年参加美术兴趣班的小学生人数为,2010年参加美术兴趣班的小学生人数为,,故C不正确,
根据扇形统计图中的比例分布,可知D正确.故选:C.
3.B
【解析】对于A选项,由于直方图的面积之和为,则,解得,A选项正确;
对于B选项,前两个矩形的面积之和为,前三个矩形的面积之和为,
设中位数为,则,则,解得,B选项错误;
对于C选项,得分在之间的频率为,C选项正确;
对于D选项,得分在之间的人数为,D选项正确.
故选:B.
4.C
【解析】A:由图知:中位数在,所以,解得,错误;
B:由图知:众数在,故众数为,错误;
C:平均数为,正确;
D:由图知:该校读书不低于本的频率之和为,所以该校读书不低于本的人数约为人.故选:C
5.D
【解析】由表可知,,
.
因为回归直线会经过平均数样本中心点,
所以=6.5×5+17.5,解得m=70.故选:D.
6.C
【解析】对于A,变量x,y之间的线性回归方程为,
而,所以变量x,y之间呈负相关关系,故选项A正确;
对于B,当时,,故选项B正确;
对于D,,所以,故D正确;
对于C,∵,∴,解得,故C不正确.
故选:C.
7.B
【解析】根据赋值语句的定义,变量=表达式,知ACD不是赋值语句,B满足.
故选:B.
8.A
【解析】运行程序框图,,;
,;
,;
…
,;
,,
因为输出,此时退出循环,所以空白框中可以填入.故选:A.
9.D
【解析】由程序框图,其执行结果如下:
1、:,执行循环体;
2、:,执行循环体;
3、:,执行循环体;
4、:,执行循环体;
5、:,跳出循环体,输出;
∴框内条件应为.故选:D.
10.C
【解析】第一次执行程序,;
第二次执行程序,;
第三次执行程序,;
第四次执行程序,,跳出循环输出,
故输出的.故选:C
11.B
【解析】从5个小球中任取2个,其中数字之差的绝对值为2或4的事件包含
(1,3),(1,5),(2,4),(3,5)4个样本点,故选:B.
12.B
【解析】从中任意取一个数,共有6种情形,两数和为偶数的情形有三种,.故选:B.
13.D
【解析】对于A选项:“至少1个红球”的事件中含有“都是红球”这一事件,即两个事件可以同时发生,A中的两个事件不互斥;
对于B选项:“恰有2个红球”和“至少1个白球”的事件中都含有“两红球,一白球”的事件,B中的两个事件不互斥;
对于C选项:“至少1个白球”与“至多1个红球”的事件中都含有“三白球”与“一红球,两白球”的两个事件,C中的两个事件不互斥;
对于D选项,3个球中“2个红球,1个白球”的事件与“2个白球,1个红球”的事件不可能同时发生,是互斥事件,所以两个事件是互斥事件的为D.故选:D
14.
【解析】由条件可知,分段间隔为:,
所以编号落入区间的人数为:
15.900
【解析】因为高一、高二、高三抽取的人数恰好组成一个以为公比的等比数列
设从高二年级抽取的学生人数为人,
则从高二、高三年级抽取的人数分别为.
由题意可得,所以.
设我校高一年级的学生人数为N,再根据,
求得.
16.5
【解析】∵-1,0,4,x,7,14的中位数为5,∴
,∴x=6.
∴这组数据的平均数是.
17.9
【解析】由所给数据可求得,,代入线性回归直线方程,得,解得,
所以线性回归直线方程,当时单位成本(元/件).
18.14
【解析】由程序框图知:第一次循环n=1,S=﹣1+1=0;
第二次循环n=2,S=0+1+2=3;
第三次循环n=3,S=3﹣1+3=5;
第四次循环n=4,S=5+1+4=10;
第五次循环n=5,S=10﹣1+5=14,
满足条件S>13,跳出循环,输出S的值为14.
19.
【解析】与对立,,
与互斥,.
20.0.8.
【解析】甲不输包括甲获胜和两人下和棋两个事件,这两个事件是互斥的。根据互斥事件的概率运算法则可知甲不输的概率是0.3+0.5=0.8.
21.11
2
【解析】对比两组数据我们发现后一组的每个数据都比前一组的每个数据多1,
所以平均数增加1,方差不变.故答案为:11;2
22.
【解析】记“第i个人抽中中奖彩票”为事件Ai
,第二个人摸到中奖彩票,指第一个人没有摸到,第二个人摸到,根据事件写出概率,第三个人摸到中奖彩票,指前两个人没有摸到,第三个人摸到,显然P(A1)=,而,.
故答案为:;
23.【解析】(1)因为,
解得,所以直方图中的值为.
(2)理科综合分数的众数是,
∵,
∴理科综合分数的中位数在内,设中位数为,
则,
解得,即中位数为.
(3)理科综合分数在的学生有(位),
同理可求理科综合分数为,
,
的用户分别有15位、10位、5位,
故抽取比为,
∴从理科综合分数在的学生中应抽取人.
24.【解析】(1),
,
,
,
,,
所以回归直线方程
(2)由回归直线方程可知,当广告费支出9万元时,
(万元),
答:销售额是76万元.
25.【解析】依题意,可设乡镇的3个脱贫村为,,,乡镇的2个脱贫村为,,乡镇的2个脱贫村为,.
从中随机抽取2个扶贫村的事件有,,,,,,,,,,,,,,,,,,,,共21种.
(1)抽取的2个村庄来自同1个乡镇的事件有,,,,,共5种,
所以抽取的2个村庄来自同1个乡镇的概率.
(2)抽取的2个村庄中至少有1个来自乡镇的事件有,,,,,,,,,,,,,,,共15种,
所以抽取的2个村庄中至少有1个来自乡镇的概率.
26.【解析】(1)甲组共有7名学生的成绩,其中位数为.
乙组成绩中,出现次数最多,故众数为.
(2)90分以上的学生共计5人,其中来自甲组有2人,
设为“随机抽取1名学生,求抽到的这名学生来自甲组”,则.
27.【解析】(1)由中位数两侧频率相等,而的频率为,的频率为,设中位数为,将分为和即有:
,解得;
(2)依据分层抽样,A组有2人为x,y,B组有3人为a,b,c,
从中任选3人,可能的情况为xya、xyb、xyc、xab
、xbc、xac、yab、ybc、yac、abc共10种情况,其中B组户数有2户的有xab、xbc、xac、yab、ybc、yac共6种,因此选出的B组户数为2的概率为.
