3.2双曲线性质及其综合运用辅导教案-2020-2021学年高二上学期数学人教A版(2019)选择性必修第一册Word无答案
文档属性
| 名称 | 3.2双曲线性质及其综合运用辅导教案-2020-2021学年高二上学期数学人教A版(2019)选择性必修第一册Word无答案 |
|
|
| 格式 | docx | ||
| 文件大小 | 184.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-24 00:00:00 | ||
图片预览



文档简介
第十一讲
双曲线的性质及其综合运用
1.双曲线的概念
平面内动点P与两个定点F1、F2(|F1F2|=2c>0)的距离之差的绝对值为常数2a(2a<2c),则点P的轨迹叫________.这两个定点叫双曲线的________,两焦点间的距离叫________.
集合P={M|||MF1|-|MF2||=2a},|F1F2|=2c,其中a、c为常数且a>0,c>0;
(1)当________时,P点的轨迹是_______;
(2)当________时,P点的轨迹是_______;
(3)当_____
__时,P点不存在.
这里要注意两点:(1)距离之差的绝对值.
(2)2a<|F1F2|.
这两点与椭圆的定义有本质的不同:
①当|MF1|-|MF2|=2a时,曲线仅表示焦点F2所对应的一支;
②当|MF1|-|MF2|=-2a时,曲线仅表示焦点F1所对应的一支;
③当2a=|F1F2|时,轨迹是一直线上以F1、F2为端点向外的两条射线;
④当2a>|F1F2|时,动点轨迹不存在.
2.双曲线的标准方程与几何性质
标准方程
-=1
(a>0,b>0)
-=1
(a>0,b>0)
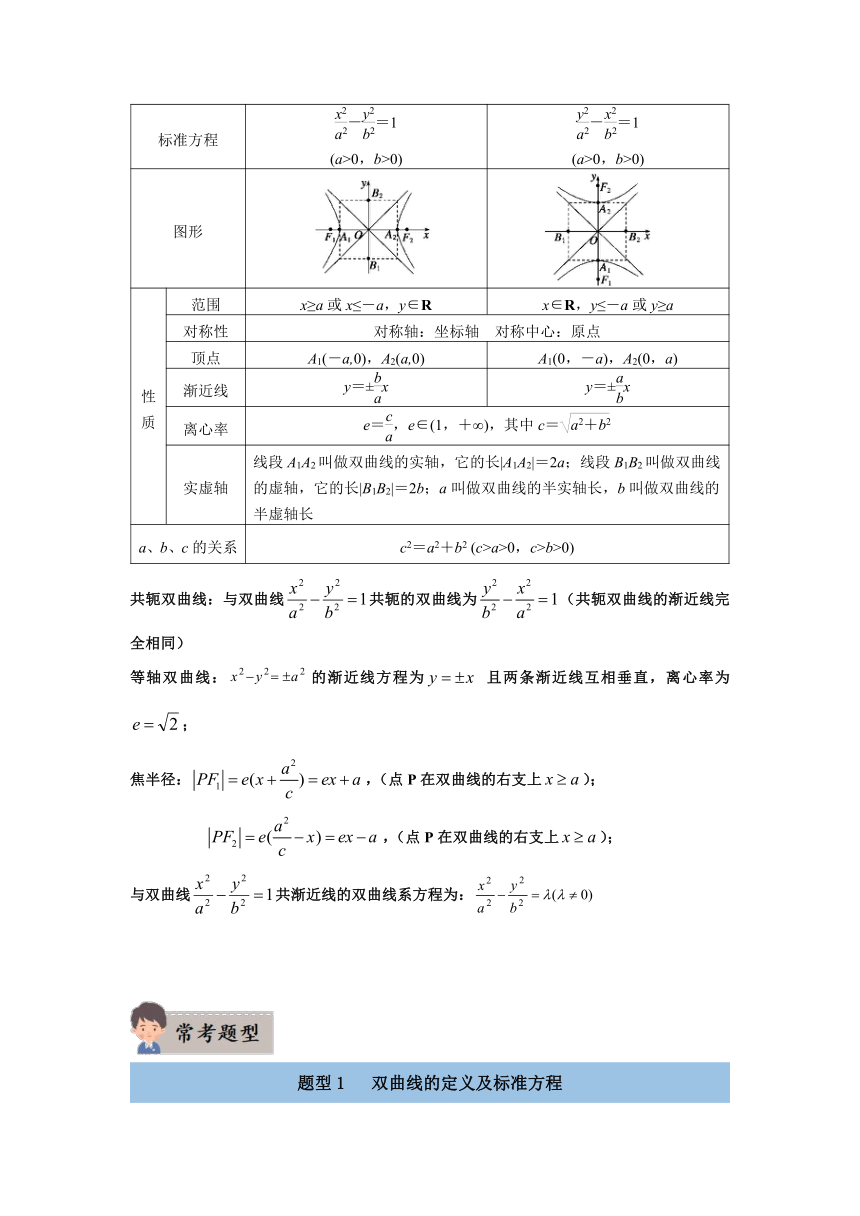
图形
性
质
范围
x≥a或x≤-a,y∈R
x∈R,y≤-a或y≥a
对称性
对称轴:坐标轴 对称中心:原点
顶点
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
渐近线
y=±x
y=±x
离心率
e=,e∈(1,+∞),其中c=
实虚轴
线段A1A2叫做双曲线的实轴,它的长|A1A2|=2a;线段B1B2叫做双曲线的虚轴,它的长|B1B2|=2b;a叫做双曲线的半实轴长,b叫做双曲线的半虚轴长
a、b、c的关系
c2=a2+b2
(c>a>0,c>b>0)
共轭双曲线:与双曲线共轭的双曲线为(共轭双曲线的渐近线完全相同)
等轴双曲线:的渐近线方程为
且两条渐近线互相垂直,离心率为;
焦半径:,(点P在双曲线的右支上);
,(点P在双曲线的右支上);
与双曲线共渐近线的双曲线系方程为:
题型1
双曲线的定义及标准方程
例1.
已知双曲线C:-=1的焦距为10,点P(2,1)在C的渐近线上,则C的方程为( )
A.-=1
B.-=1
C.-=1
D.-=1
练习1.已知双曲线x2-y2=1,点F1,F2为其两个焦点,点P为双曲线上一点,若PF1⊥PF2,则|PF1|+|PF2|的值为________.
例2.已知双曲线C与双曲线-=1有公共焦点,且过点(3,2),求双曲线C的方程
例3.与双曲线-=1有共同的渐近线,且过点(-3,2),求双曲线的标准方程.
例4.与椭圆焦点相同的等轴双曲线的标准方程为__________________.
练习2.过点的等轴双曲线的标准方程为____________________.
题型2
双曲线的离心率与渐近线问题
例5.此双曲线的一条渐近线与x轴的夹角为α,且<α<,求双曲线的离心率的取值范围.
例6.已知双曲线-=1(a>0,b>0)的离心率e=,则一条渐近线与实轴所成锐角的值是________.
例7.双曲线C:的离心率为2,焦点到渐近线的距离为,则C的焦距等于(
)
A.
2
B.
C.4
D.
练习3.已知双曲线-=1(a>0,b>0)的右焦点为F,若过点且斜率为的直线与双曲线渐近线平行,则此双曲线离心率是( )
A.
B.
C.2
D.2
题型3
点、直线与双曲线的位置关系
点与双曲线的位置关系
先将点P的坐标代入计算结果,然后与1比较大小:
;
;
.
直线与双曲线的位置关系
直线与双曲线方程联立,通过联立方程的判别式来判断直线与双曲线的位置关系,
;
;(直线与渐近线平行的话就相交,直线与渐近线不平行就相切)
.
特别注意:直线与双曲线交于一点时,不一定相切,例如:当直线与双曲线的渐近线平行时,直线与双曲线相交于一点,但不是相切;反之,当直线与双曲线相切时,直线与双曲线仅有一个交点.
例8.判断直线与双曲线的位置关系.
例9.已知双曲线-=1(b>a>0),O为坐标原点,离心率e=2,点M(,)在双曲线上.
(1)求双曲线的方程;
(2)若直线l与双曲线交于P,Q两点,且·=0.求+的值.
题型4
双曲线的焦点三角形
双曲线的焦点三角形面积公式:;
双曲线周长公式:设点,当双曲线的焦点在轴上时,;
当双曲线的焦点在轴上时,.
例10.已知双曲线,A,B是其两个焦点,点在双曲线上,,则三角形AMB的面积为_____________.
例11.已知双曲线上一点的坐标为,则其与双曲线的两个焦点所围成的的周长为______________.
题型5
双曲线的弦长问题
弦长公式:
,其长度为.
例12.已知一双曲线中心在原点,焦点在轴,直线与双曲线所截得的弦长为,且以为直径的圆过原点,求双曲线的方程.
题型6
双曲线的中点弦问题
“由弦的中点坐标,求弦所在的直线方程或相关问题,叫做中点弦问题”
根与系数的关系法:联立直线方程和双曲线方程,得到一个关于的一元二次方程,利用一元二次方程根与系数的关系和中点坐标公式解决问题.
点差法:利用交点在曲线上,坐标满足方程,将交点坐标分别代入双曲线方程,然后作差,构造出中点坐标和斜率的关系;已知,是双曲线上的两个不同的点,是线段的中点,
则
由①-②,得,
变形得,即.
共线法:利用中点坐标公式,如果弦的中点为,设其一交点为,则另一交点为,则,作差即得所求直线方程.
例13.过点作直线交双曲线于两点,且点恰为线段中点,则直线的方程为_____________________.
练习4.已知双曲线-y2=1,求过点A
(3,-1)且被点A平分的弦MN所在直线的方程.
例14.在平面直角坐标系中,已知双曲线的焦点为、,实轴长为.
(1)求双曲线的标准方程;
(2)过点的直线与曲线交于,两点,且恰好为线段的中点,求直线的方程及弦的长.
双曲线的性质及其综合运用
1.双曲线的概念
平面内动点P与两个定点F1、F2(|F1F2|=2c>0)的距离之差的绝对值为常数2a(2a<2c),则点P的轨迹叫________.这两个定点叫双曲线的________,两焦点间的距离叫________.
集合P={M|||MF1|-|MF2||=2a},|F1F2|=2c,其中a、c为常数且a>0,c>0;
(1)当________时,P点的轨迹是_______;
(2)当________时,P点的轨迹是_______;
(3)当_____
__时,P点不存在.
这里要注意两点:(1)距离之差的绝对值.
(2)2a<|F1F2|.
这两点与椭圆的定义有本质的不同:
①当|MF1|-|MF2|=2a时,曲线仅表示焦点F2所对应的一支;
②当|MF1|-|MF2|=-2a时,曲线仅表示焦点F1所对应的一支;
③当2a=|F1F2|时,轨迹是一直线上以F1、F2为端点向外的两条射线;
④当2a>|F1F2|时,动点轨迹不存在.
2.双曲线的标准方程与几何性质
标准方程
-=1
(a>0,b>0)
-=1
(a>0,b>0)
图形
性
质
范围
x≥a或x≤-a,y∈R
x∈R,y≤-a或y≥a
对称性
对称轴:坐标轴 对称中心:原点
顶点
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
渐近线
y=±x
y=±x
离心率
e=,e∈(1,+∞),其中c=
实虚轴
线段A1A2叫做双曲线的实轴,它的长|A1A2|=2a;线段B1B2叫做双曲线的虚轴,它的长|B1B2|=2b;a叫做双曲线的半实轴长,b叫做双曲线的半虚轴长
a、b、c的关系
c2=a2+b2
(c>a>0,c>b>0)
共轭双曲线:与双曲线共轭的双曲线为(共轭双曲线的渐近线完全相同)
等轴双曲线:的渐近线方程为
且两条渐近线互相垂直,离心率为;
焦半径:,(点P在双曲线的右支上);
,(点P在双曲线的右支上);
与双曲线共渐近线的双曲线系方程为:
题型1
双曲线的定义及标准方程
例1.
已知双曲线C:-=1的焦距为10,点P(2,1)在C的渐近线上,则C的方程为( )
A.-=1
B.-=1
C.-=1
D.-=1
练习1.已知双曲线x2-y2=1,点F1,F2为其两个焦点,点P为双曲线上一点,若PF1⊥PF2,则|PF1|+|PF2|的值为________.
例2.已知双曲线C与双曲线-=1有公共焦点,且过点(3,2),求双曲线C的方程
例3.与双曲线-=1有共同的渐近线,且过点(-3,2),求双曲线的标准方程.
例4.与椭圆焦点相同的等轴双曲线的标准方程为__________________.
练习2.过点的等轴双曲线的标准方程为____________________.
题型2
双曲线的离心率与渐近线问题
例5.此双曲线的一条渐近线与x轴的夹角为α,且<α<,求双曲线的离心率的取值范围.
例6.已知双曲线-=1(a>0,b>0)的离心率e=,则一条渐近线与实轴所成锐角的值是________.
例7.双曲线C:的离心率为2,焦点到渐近线的距离为,则C的焦距等于(
)
A.
2
B.
C.4
D.
练习3.已知双曲线-=1(a>0,b>0)的右焦点为F,若过点且斜率为的直线与双曲线渐近线平行,则此双曲线离心率是( )
A.
B.
C.2
D.2
题型3
点、直线与双曲线的位置关系
点与双曲线的位置关系
先将点P的坐标代入计算结果,然后与1比较大小:
;
;
.
直线与双曲线的位置关系
直线与双曲线方程联立,通过联立方程的判别式来判断直线与双曲线的位置关系,
;
;(直线与渐近线平行的话就相交,直线与渐近线不平行就相切)
.
特别注意:直线与双曲线交于一点时,不一定相切,例如:当直线与双曲线的渐近线平行时,直线与双曲线相交于一点,但不是相切;反之,当直线与双曲线相切时,直线与双曲线仅有一个交点.
例8.判断直线与双曲线的位置关系.
例9.已知双曲线-=1(b>a>0),O为坐标原点,离心率e=2,点M(,)在双曲线上.
(1)求双曲线的方程;
(2)若直线l与双曲线交于P,Q两点,且·=0.求+的值.
题型4
双曲线的焦点三角形
双曲线的焦点三角形面积公式:;
双曲线周长公式:设点,当双曲线的焦点在轴上时,;
当双曲线的焦点在轴上时,.
例10.已知双曲线,A,B是其两个焦点,点在双曲线上,,则三角形AMB的面积为_____________.
例11.已知双曲线上一点的坐标为,则其与双曲线的两个焦点所围成的的周长为______________.
题型5
双曲线的弦长问题
弦长公式:
,其长度为.
例12.已知一双曲线中心在原点,焦点在轴,直线与双曲线所截得的弦长为,且以为直径的圆过原点,求双曲线的方程.
题型6
双曲线的中点弦问题
“由弦的中点坐标,求弦所在的直线方程或相关问题,叫做中点弦问题”
根与系数的关系法:联立直线方程和双曲线方程,得到一个关于的一元二次方程,利用一元二次方程根与系数的关系和中点坐标公式解决问题.
点差法:利用交点在曲线上,坐标满足方程,将交点坐标分别代入双曲线方程,然后作差,构造出中点坐标和斜率的关系;已知,是双曲线上的两个不同的点,是线段的中点,
则
由①-②,得,
变形得,即.
共线法:利用中点坐标公式,如果弦的中点为,设其一交点为,则另一交点为,则,作差即得所求直线方程.
例13.过点作直线交双曲线于两点,且点恰为线段中点,则直线的方程为_____________________.
练习4.已知双曲线-y2=1,求过点A
(3,-1)且被点A平分的弦MN所在直线的方程.
例14.在平面直角坐标系中,已知双曲线的焦点为、,实轴长为.
(1)求双曲线的标准方程;
(2)过点的直线与曲线交于,两点,且恰好为线段的中点,求直线的方程及弦的长.
