4.4求数列前n项和辅导教案-2020-2021学年高二下学期数学人教A版(2019)选择性必修第二册(Word无答案)
文档属性
| 名称 | 4.4求数列前n项和辅导教案-2020-2021学年高二下学期数学人教A版(2019)选择性必修第二册(Word无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 143.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-24 21:11:31 | ||
图片预览



文档简介
第五讲
求数列前n项和
1.公式法求前n项和
利用下列常用求和公式求和是数列求和的最基本最重要的方法
(1)等差数列求和公式:
(2)等比数列求和公式:
注意:运用等比数列求和公式,务必检查其公比与1的关系,必要时需分类讨论
(3)常用公式:,,
.
2.分组求和法
在直接运用公式法求和有困难时,常将“和式”中“同类项”先合并在一起,再运用公式法求和.
3.倒序相加法
若和式中到首尾距离相等的两项和有其共性或数列的通项与组合数相关联,则常可考虑选用倒序相加法,发挥其共性的作用求和(这也是等差数列前和公式的推导方法).
4.裂项相消法
如果数列的通项可“分裂成两项差”的形式,且相邻项分裂后相关联,那么常选用裂项相消法求和.常用裂项形式有:
,
,
,
5.错位相减法
如果数列的通项是由一个等差数列的通项与一个等比数列的通项相乘构成,那么常选用错位相减法(这也是等比数列前和公式的推导方法).
题型1
公式法求前n项和
例1.已知,求的前项和.
练习1.等比数列的前项和,则
题型2
分组法求和
例2.设等比数列的前项和为,已知,.
(1)求数列的通项公式;
(2)设数列的前项和为,求.
练习2.求数列的前项和;
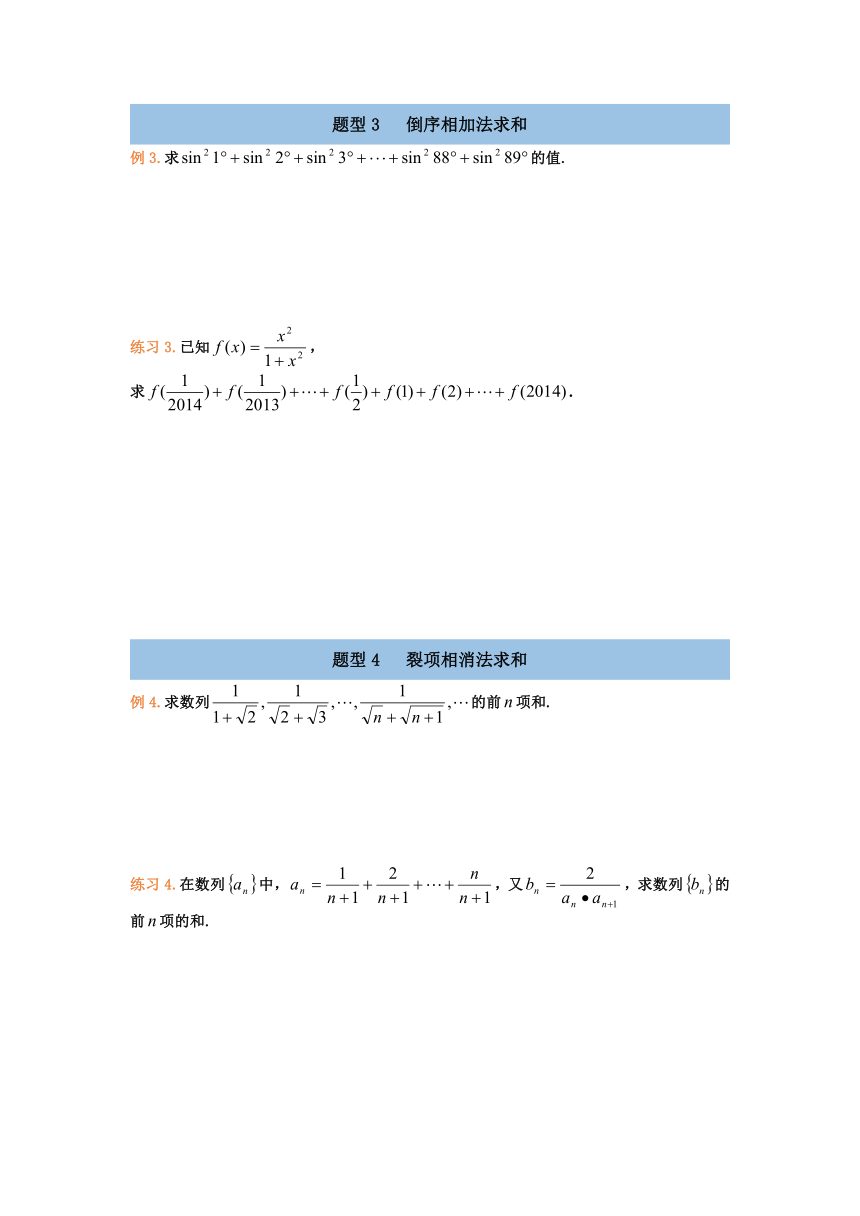
题型3
倒序相加法求和
例3.求的值.
练习3.已知,
求.
题型4
裂项相消法求和
例4.求数列的前项和.
练习4.在数列中,,又,求数列的前项的和.
练习5.求和
例5.已知数列是正项等比数列,满足,.
(1)求的通项公式;
(2)设,求数列的前项和.
题型5
错位相减法求和
例6.求和
练习6.求数列前项的和.
例7.在等比数列中,为的前项和,且,,
(1)求.
(2)求数列的前项和.
练习7.设为等比数列,,已知,①求数列的首项和公比;
②求数列的通项公式.
题型6
通项转换法求和
例8.求之和.
练习8.求数列前项和
练习9.求和
课后作业
.
求数列前n项和
1.公式法求前n项和
利用下列常用求和公式求和是数列求和的最基本最重要的方法
(1)等差数列求和公式:
(2)等比数列求和公式:
注意:运用等比数列求和公式,务必检查其公比与1的关系,必要时需分类讨论
(3)常用公式:,,
.
2.分组求和法
在直接运用公式法求和有困难时,常将“和式”中“同类项”先合并在一起,再运用公式法求和.
3.倒序相加法
若和式中到首尾距离相等的两项和有其共性或数列的通项与组合数相关联,则常可考虑选用倒序相加法,发挥其共性的作用求和(这也是等差数列前和公式的推导方法).
4.裂项相消法
如果数列的通项可“分裂成两项差”的形式,且相邻项分裂后相关联,那么常选用裂项相消法求和.常用裂项形式有:
,
,
,
5.错位相减法
如果数列的通项是由一个等差数列的通项与一个等比数列的通项相乘构成,那么常选用错位相减法(这也是等比数列前和公式的推导方法).
题型1
公式法求前n项和
例1.已知,求的前项和.
练习1.等比数列的前项和,则
题型2
分组法求和
例2.设等比数列的前项和为,已知,.
(1)求数列的通项公式;
(2)设数列的前项和为,求.
练习2.求数列的前项和;
题型3
倒序相加法求和
例3.求的值.
练习3.已知,
求.
题型4
裂项相消法求和
例4.求数列的前项和.
练习4.在数列中,,又,求数列的前项的和.
练习5.求和
例5.已知数列是正项等比数列,满足,.
(1)求的通项公式;
(2)设,求数列的前项和.
题型5
错位相减法求和
例6.求和
练习6.求数列前项的和.
例7.在等比数列中,为的前项和,且,,
(1)求.
(2)求数列的前项和.
练习7.设为等比数列,,已知,①求数列的首项和公比;
②求数列的通项公式.
题型6
通项转换法求和
例8.求之和.
练习8.求数列前项和
练习9.求和
课后作业
.
